高精度石英挠性加速度计力矩器磁路仿真分析
2021-11-05李军朔冯东棉王文一
杜 剑,张 阳,李军朔,冯东棉,王文一
(中国航天科技集团公司第十六研究所,西安710100)
0 引言
作为惯性导航系统的关键传感器单元,石英挠性加速度计主要用来对运载体受到的惯性加速度力进行测量[1-3],其误差水平直接决定着惯性系统的导航精度。石英挠性加速度计工作时,力矩器的气隙磁场为检测质量的动圈提供电磁反馈力以平衡惯性力,其内部磁场的性能对加速度计的精度有着重要影响。其中,加速度计标度因数的非线性误差主要来源于力矩器磁性能的非线性变化[1]。同时,力矩器内永磁体磁性能随温度发生的变化也会引起加速度计参数的漂移[4-6]。根据总体型号要求,高精度加速度计标度因数的非线性误差指标已达10-5~10-6量级,因此力矩器磁路优化设计的重要性不言而喻。
加速度计力矩器的磁路设计得到了广泛的关注。王晓东等[7]使用三维模型对加速度计装配及制造过程对力矩器磁性能指标偏差的影响进行了研究,为指导加速度计零件生产及装配工艺提供了方法。杨峰等[8]建立了加速度计力矩器二维模型,分析了不同长径比永磁体对加速度计标度因数长期重复性的影响。黄小凯等[9]运用模糊理论给出了力矩器及石英摆片三角模糊数区间,采用磁-结构耦合有限元仿真得到了温度变化过程加速度计标度因数模糊输出区间,说明了该方法对提高加速度计标度因数长期稳定性的意义。葛颂等[10]在试验对比验证补偿环对工作力矩器工作气隙磁密的影响基础上实现了补偿环尺寸的合理优化。
总结上述内容,目前开展的研究工作涉及加速度计标度因数非线性误差及温度系数仿真的内容较少。本文主要针对某型号高精度石英挠性加速度计设计应用,以减小非线性误差为目标对使用新型钐钴磁钢的加速度计力矩器磁路进行优化,同通过仿真对力矩器气隙磁密的温度系数进行探索性计算。
1 石英挠性加速度计的工作原理
加速度计工作时,由摆片及动圈组成的检测质量来敏感输入加速度。当加速度计的输入轴方向存在加速度载荷时,检测质量在惯性力作用下偏离平衡位置,绕挠性枢轴做偏摆运动。由此,上下轭铁与摆片构成的差动电容传感器产生差动电容,由伺服电路的差动电容检测器转换为电流,再经过积分放大后成为平衡电流输出给力矩器动圈,通电动圈在力矩器的气隙磁场中受到电磁力,形成与惯性力矩数值相等、方向相反的平衡力矩,迫使检测质量回到平衡位置。平衡电流的大小与检测质量敏感到的加速度成正比,通过测出平衡电流的大小即可得到输入的加速度量级。
检测质量中的动圈处于力矩器永磁体提供的恒定磁场中,该磁场为动圈产生电磁力的能量来源,故力矩器的磁性能对加速度计精度有着直接的影响。在设计时,既要保证力矩器气隙磁场强度足够大,又要保证动圈所处工作区间磁场强度的均匀性,以减小力矩器磁路带来的非线性误差,保证加速度计在大过载条件下的精度;另一方面,又要兼顾力矩器气隙磁密的温度系数,保证加速度计在全温度范围下的测试精度。
2 加速度计力矩器的磁路设计
2.1 加速度计力矩器的工作原理
石英挠性加速度计力矩器为永磁动圈式力矩器,其结构示意图如图1所示。磁钢一般采用铝镍钴永磁体或钐钴永磁体,采用轴向充磁。为了提高磁路的线性度,采用两个力矩器磁钢同极性对顶的推挽结构,两个磁路相互独立,相互补偿,在轭铁与磁钢组件之间的气隙(即动圈的工作区域)形成均匀磁场,这样既减小了轴向漏磁,提高了磁钢的利用率,又可以补偿因材料导致磁性能不均匀及加工不对称等因素带来的非线性。当沿加速度计输入轴方向有加速度作用时,由处于力矩器气隙磁场中的动圈产生反馈电磁力矩,与输入加速度引起的惯性力矩相平衡[11]。
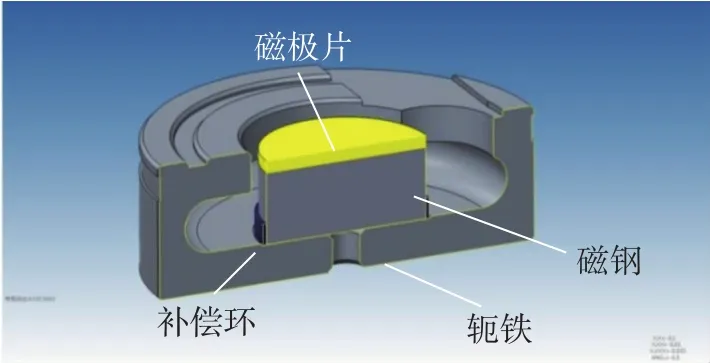
图1 力矩器结构示意图Fig.1 Structure diagram of torquer
以单动圈力矩器为例,其输出电磁力矩的表达式为

式(1)中,Bσ为动圈所处工作气隙的磁感应强度,I为动圈中流经的电流,l为线圈的有效长度,W为线圈匝数,R为线圈至挠性轴的平均半径,K为力矩器的标度因数。
加速度计的标度因数K1的计算公式为

式(2)中,P为加速度计的摆性。由式(1)、式(2)可知,石英挠性加速度计的标度因数与力矩器的机电能量转换的桥梁——气隙磁密紧密相关。
2.2 加速度计力矩器磁路计算原理
由图1可知,加速度计力矩器的闭合磁路主要由永磁体与线圈工作气隙、永磁体与磁极片及轭铁组成。其中,永磁体尺寸的计算主要借助于Gauss磁通定律与磁路的Kirchhoff第二定律。根据Gauss磁通定律,可得
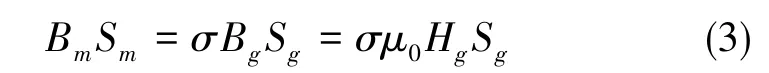
根据磁路的Kirchhoff第二定律,可得

式(3)、式(4)中,Lg、Sg为线圈工作气隙的厚度和横截面积,Hg与Bg为磁路工作气隙的磁场强度和磁感应强度,Hm与Bm为永磁体产生的磁场强度和磁感应强度,Lm与Sm为永磁体的高度和横截面积,f为磁阻系数,σ为漏磁系数,μ0为真空磁导率。由式(3)、式(4)可得
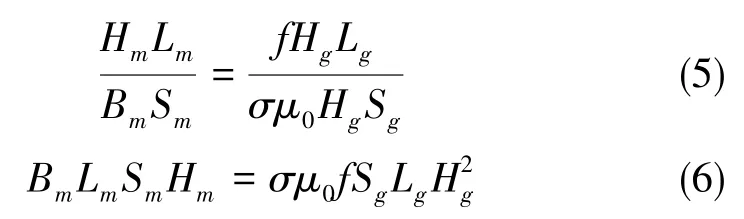
又因永磁体体积Vm=LmSm,由式(6)可得
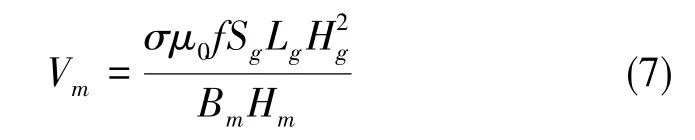
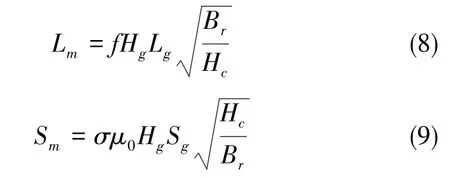
3 加速度计力矩器磁路的仿真计算
3.1 力矩器磁路的有限元仿真原理及方法
在使用传统方法进行力矩器磁路计算时,经验系数的选取对计算结果的准确性很关键,这往往需要进行多次调整复核计算。现代数值分析计算方法为加速度计力矩器磁场问题的分析和求解提供了便捷、强有力的支持,本文使用有限元分析法对Maxwell微分方程进行求解,采用三角形剖分单元将求解区域剖分离散,引入矢量磁位A,并在每个离散单元构造矢量磁位的插值函数,通过插值方法将求解的条件变分问题离散为多元函数的极值问题,同时附加边界定解条件,可求解得到磁势和电势的场分布值,进而可转化得到电磁场中磁感应强度、力等物理量的值。如图2所示,为减小计算工作量和求解规模,考虑到力矩器的对称性,建立加速度计力矩器磁路计算的简化有限元模型,使用静磁场求解器对其内部磁通分布进行计算。

图2 加速度计力矩器磁路的有限元计算模型Fig.2 Magnetic circuit finite element model of the accelerometer torquer
静磁场计算的求解步骤为:
1)创建物理计算环境,导入有限元分析模型;
2)对求解域划分网格,并对模型不同部位对应域赋予特性;
3)设定边界条件和求解参数;
4)求解计算及结果后处理。
3.2 仿真计算
高精度石英挠性加速度计力矩器设计时,磁钢一般选用铝镍钴或者钐钴磁钢。为了验证仿真计算的正确性,使用某型号铝镍钴磁钢装配力矩器(未对顶装配,方便气隙磁密测试),对其气隙磁密进行实测,并与仿真计算结果进行对比。气隙磁密仿真计算结果如图3所示,力矩器气隙磁密实测值与仿真值对比如表1所示。

表1 仿真值与实测值误差对比Table 1 Error comparison of simulated values and measured values
由表1可知,仿真值与实测值之间的误差为0.38%,在误差允许范围内,可验证仿真结果的正确性。
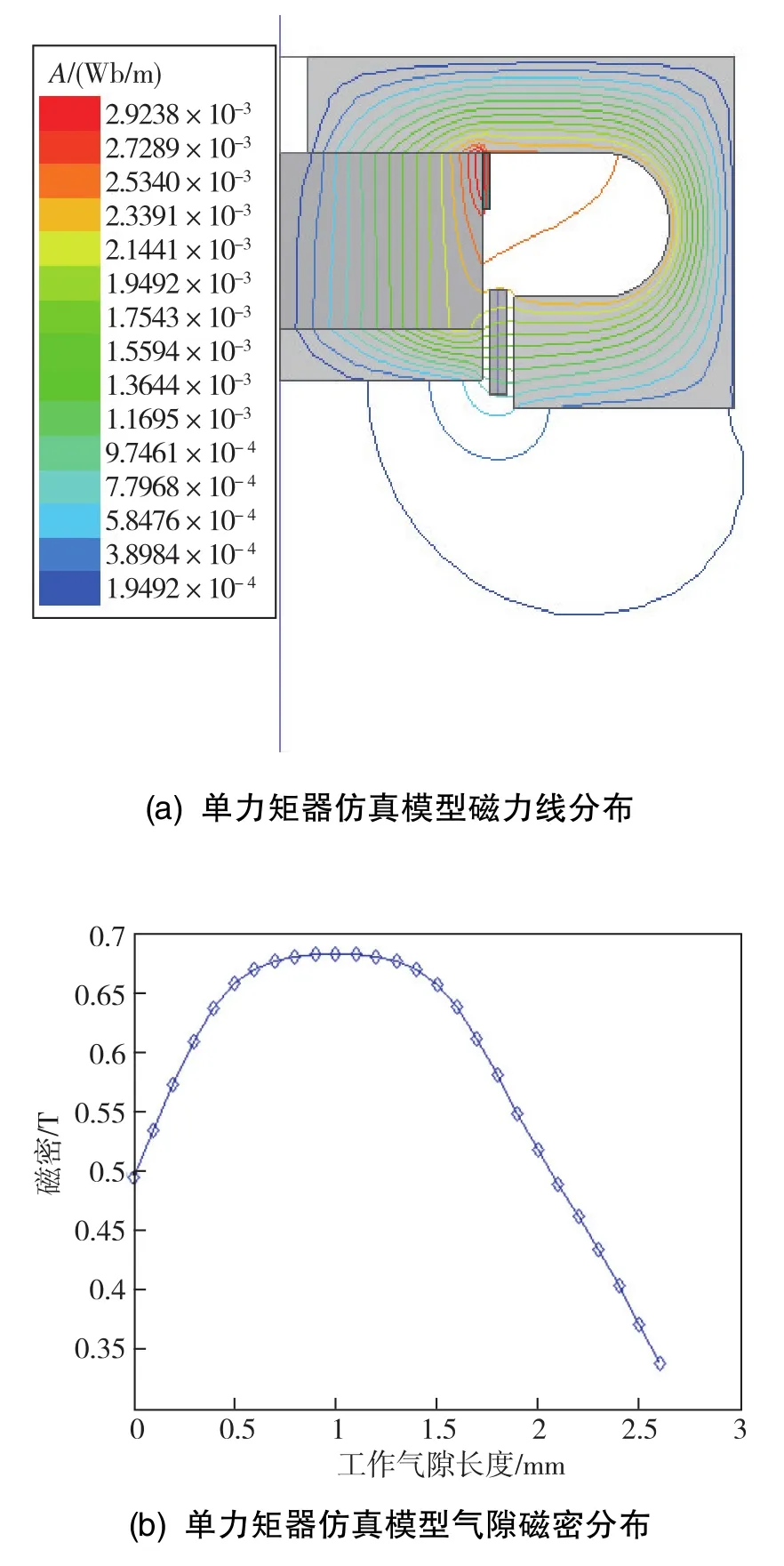
图3 力矩器磁场仿真结果Fig.3 Simulation results of torquer magnetic field
3.3 仿真计算结果与分析
为提高石英挠性加速度计的长期稳定性,保证其全温度范围内的精度,选用某牌号高矫顽力、高磁能积、低可逆温度系数的钐钴磁钢进行方案验证。为保证充分利用该钐钴磁钢的性能,有必要对其力矩器磁路进行再设计。
如图4所示,为使用力矩器的1/4二维有限元模型,对装配上述钐钴磁钢力矩器的推挽结构及单力矩器的磁场仿真结果进行对比。由于加速度计摆组件运动方向为沿输入轴方向,动圈在磁场中受到的电磁反馈力亦沿输入轴方向,由Lorentz力的计算公式可知,在对力矩器气隙磁密计算时应主要关注其径向分量Bx, 其受力计算公式为

图4 推挽结构与单力矩器结构的磁路仿真结果Fig.4 Magnetic circuit simulation results of the push-pull structure torquer and the single torque

结果表明,相比单力矩器,采用推挽式结构时,力矩器工作气隙漏磁明显减小,气隙磁密Bx的值及其线性工作区长度均得到提高,相比图3使用铝镍钴磁钢时,气隙磁密增大了约47%。由图4(d)可知,靠近力矩器线圈工作气隙位置的磁极片尖角磁密接近3.05T,已达到饱和[9],其工作在不正常导磁状态,不利于在力矩器气隙形成均匀磁场,会放大标度因数的非线性误差,故有必要对使用新磁钢的磁路进行计算优化。
使用力矩器推挽结构的1/4二维有限元模型,在磁钢和磁极片总厚度不变的前提下,对磁钢、磁极片不同厚度尺寸配比的四种方案下的力矩器磁路进行计算,如表2所示,其气隙磁密结果如图5、图6所示。

表2 磁钢、磁极片的不同配比方案Table 2 Different matching schemes of PM and pole pieces
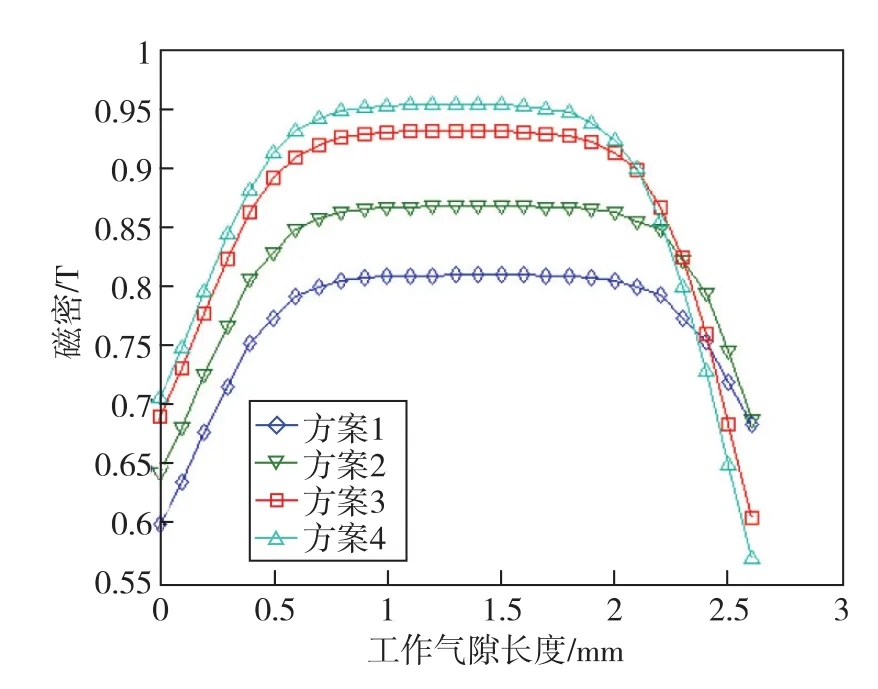
图5 不同结构方案的力矩器磁路仿真对比Fig.5 Simulation comparison of torquer magnetic circuit with different structure schemes

图6 不同力矩器结构磁极片磁密对比Fig.6 Magnetic density comparison of pole piece with different torquer structures
结果表明,随着磁钢与磁极片厚度比的增加,力矩器气隙磁密值逐渐增大,但其线性区域长度随之减小。其中,方案4的磁极片尖角处磁密仍接近饱和磁密值,而方案3、方案2及方案1的磁极片未出现该现象。方案2相比未优化前的气隙磁密线性长度增加了72%,综合方案中加速度计标度因数设计值和量程,方案2为最优结构,其气隙磁密大小满足要求,又获得了足够的磁密线性区域长度。
在精密离心机上对使用方案2结构的加速度计在大过载下的输出进行测试,并依据最小二乘法对输出值进行拟合,同时对二阶非线性误差系数进行辨识。加速度计在全量程下的输出实际值与拟合值的误差情况如图7所示,经计算其二阶非线性误差优于5×10-6,从而证明了上述磁路设计方案选择的合理性。
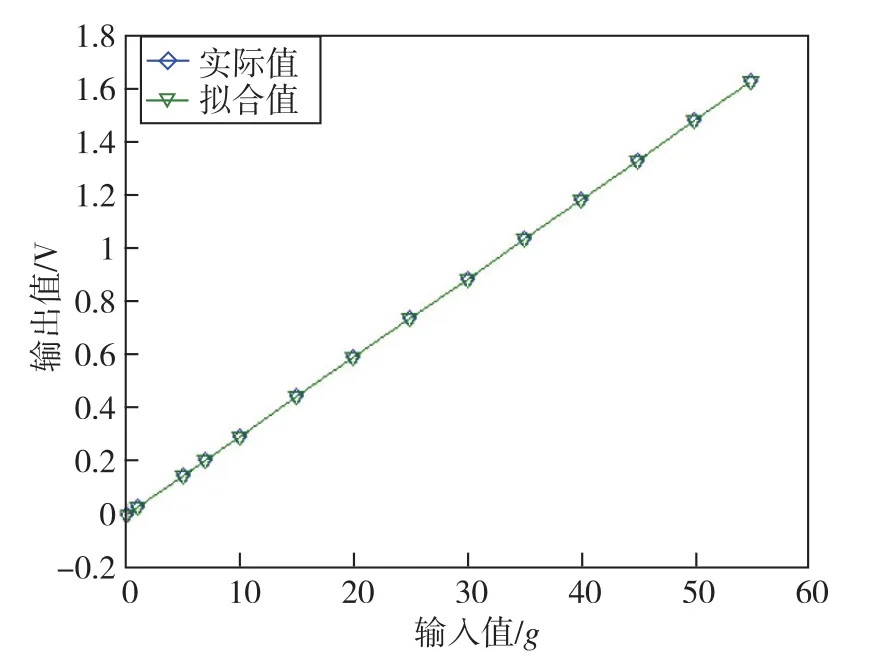
图7 加速度计全量程的输出值与拟合值Fig.7 Diagram of accelerometer full range output value and fitting value
为快速得到该低温度系数磁钢在高精度加速度计中应用的温度系数效果,可通过力矩器有限元仿真模型求解其气隙磁密在不同温度点的变化情况,由此得到加速度计标度因数的温度系数。力矩器气隙磁密在20℃与50℃时(不考虑补偿环补偿效果)的仿真结果对比如图8所示。
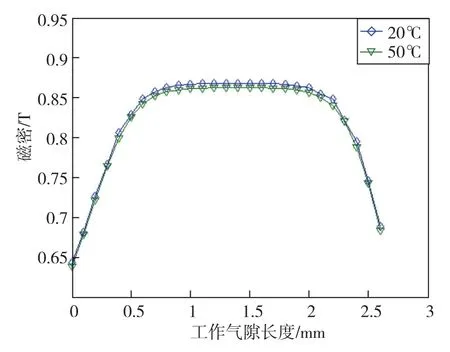
图8 不同温度下的气隙磁密对比Fig.8 Comparison of air gap magnetic density at different temperatures
结果表明,使用该低温度系数磁钢的力矩器在两种工作温度下的气隙磁密线性工作区长度基本一致,磁密大小差值约为2.8mT,由此可得在20℃与 50℃下力矩器气隙磁密的温度系数为0.011%/℃,与磁钢的温度系数相当。该结果验证了仿真计算的正确性,为仿真求解加速度计标度因数的温度系数奠定了基础。
4 结论
随着现代导航技术发展对加速度计精度要求的不断提升,加速度计设计开发选用新型高性能材料时有必要对原方案进行再设计。本文对某型号高精度石英挠性加速度计力矩器磁路特性进行计算,并以实测数据证明了方案选择的正确性。结果表明,在加速度计力矩器磁路设计时,延长力矩器工作气隙径向磁密的线性区间对减小加速度计二阶非线性误差是十分有效的,同时通过有限元仿真分析法可实现在设计阶段对加速度计力矩器气隙磁密的温度系数进行定量计算,进而实现标度因数温度系数的有效预测,为缩短设计开发周期提供了新思路。
