内S形柔性梁多环谐振陀螺热弹性阻尼分析

冯 军， 张卫平， 刘朝阳， 谷留涛

(1.微米／纳米加工技术国家重点实验室，上海200240；2.上海交通大学电子信息与电气工程学院微纳电子学系，上海200240)

0 引言

随着微机电系统(Micro Electro Mechanical System，MEMS)技术的发展，MEMS陀螺以其体积小、功耗低、适合批量生产等优势受到广泛关注。波音公司提出的多环谐振陀螺由于其结构对称好、响应灵敏度高、抗冲击能力强等优势，成为了目前MEMS陀螺领域的研究热点[1-3]。在传统多环谐振陀螺的基础上，内S形柔性梁多环谐振陀螺将最内层的直线形支撑梁改为S形支撑梁，可降低谐振频率从而提高响应灵敏度。针对内S形柔性梁多环谐振陀螺的工作原理和加工工艺已经做了相关研究[4]，但尚未有该陀螺性能方面的报道。对于MEMS谐振陀螺而言，品质因数是一个关键的技术指标，对于陀螺的性能至关重要[5]。品质因数的大小由陀螺中的能量耗散决定，其能量耗散的主要形式有空气阻尼、锚点阻尼、热弹性阻尼等[6-7]。由于内S形柔性梁多环谐振陀螺采用真空封装，气体压强的影响可以忽略不计，因而空气阻尼不是主要的能量耗散形式。此外，内S形柔性梁多环谐振陀螺具有良好的对称结构，其锚点附近的振动十分微弱，锚点阻尼的影响也可以忽略。综上，热弹性阻尼是内S形柔性梁多环谐振陀螺中主要的能量耗散机制。

为提高内S形柔性梁多环谐振陀螺的性能，首先需要分析该陀螺中热弹性阻尼的机理。此外，由于热弹性阻尼与陀螺结构有着密切关联，找出各结构参数与热弹性阻尼的关系对于设计高性能的陀螺结构十分重要。因此，本文主要针对以上两点对热弹性阻尼进行分析，并提供内S形柔性梁多环谐振陀螺结构设计的合理建议。

1 结构与工作原理

内S形柔性梁多环谐振陀螺由谐振器和外围电极构成，其结构示意图如图1(a)所示。中央圆盘通过锚点与基底固定，多个同心圆环之间通过轮辐状支撑梁相连接。其中，连接最内层圆环与中央圆盘之间的支撑梁为S形结构，其余支撑梁为直线结构。谐振器的主要结构参数标注如图1(b)所示。其中，S形支撑梁由两段相同的圆弧组成，每段圆弧的圆心角均为α；谐振器的最外层环半径为R1，最内层环半径为R2，中央圆盘的半径为r，同心圆环的宽度为W1，直线形和S形支撑梁宽度均为W2。另将谐振器厚度记为H，同心圆环的个数记为N。

图1 陀螺结构及主要结构参数示意图Fig.1 Schematic diagram of gyroscope structure and its main structure parameters

内S形柔性梁多环谐振陀螺基于科氏效应工作，通过在外围电极上施加驱动电压产生驱动力，从而使得陀螺在驱动轴方向产生振动。当存在垂直于面外方向的角速度输入时，由于科氏力的作用，陀螺会产生检测轴方向的振动，由于谐振子与外围电极形成平行板电容器，两极板的距离随振动发生变化，通过检测电容的变化就能测量出输入的角速度大小。为了便于陀螺的信号检测和控制，通常采用面内振动的四波腹模态作为驱动和检测的工作模态，如图2所示。

图2 陀螺的工作模态Fig.2 Diagram of gyroscope working modal

2 热弹性阻尼的计算

MEMS谐振陀螺的能量耗散大小可以用品质因数Q来表示[8]

式(1)中，W0为振动中存储的总能量，ΔW为每个振动周期所耗散的能量。由式(1)可知，能量耗散越小，则品质因数越大。热弹性阻尼是由于振动导致器件弯曲变形而产生的，受拉伸的部分温度下降，受压缩的部分温度升高，从而在器件中产生不可逆的热流，导致振动能量的耗散。热弹性阻尼造成的能量耗散可以用热弹性阻尼的品质因数QTED来表示。

热弹性阻尼的大小可以通过下面的耦合热弹性方程来求解[9]

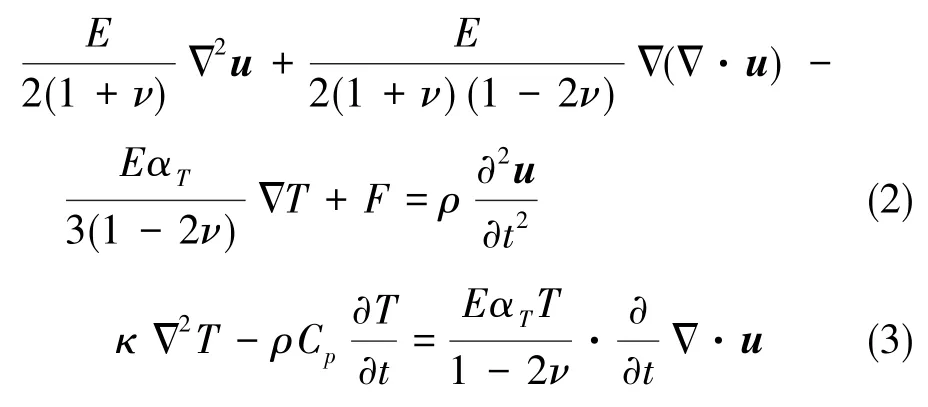
式(2)、式(3)中，E为弹性模量，ν为泊松比，αT为热膨胀系数，ρ为密度，κ为导热系数，Cp为恒压热容，F为单位体积力，u为位移矢量，T为温度。本文研究的内S形柔性梁多环谐振陀螺的材料为各向同性单晶硅，其材料参数如表1所示。

表1 各向同性单晶硅的材料参数Table 1 Material parameters of isotropic single crystal silicon

对于内S形柔性梁多环谐振陀螺，由于其结构比较复杂，采用解析方法计算上述耦合热弹性方程十分困难，可借助有限元软件COMSOL Multiphysics对上述耦合热弹性方程进行数值计算。COMSOL Multiphysics中的热弹性力学将应力场和温度场进行了耦合，可用于耦合热弹性问题的分析。

通过有限元仿真分析，可以得出如图3所示的四波腹模态的温度分布图，并可求出热弹性阻尼的品质因数QTED。

图3 四波腹模态中的温度分布Fig.3 Diagram of temperature distribution in four-antinode modal

由图3可知，由于陀螺的弯曲变形，谐振器各处温度不同，从而形成从高温区域到低温区域的不可逆热流。这些热流的形成受陀螺结构的影响很大，研究结构参数对热弹性阻尼的影响是十分必要的。

由图2和图3可知，由于中央圆盘与基底固定，中央圆盘处没有振动位移和温度梯度，故有限元模型中可以将中央圆盘去除，同时在S形支撑梁与中央圆盘连接处的8个截面添加固定约束，以等效于中央圆盘与基底固定。等效后的有限元模型如图4所示。在该有限元模型中，采用三角形网格和扫掠网格相结合的网格划分方法，既满足了网格划分的灵活性要求，又能提高计算的精度和速度。在实际计算过程中，需要进一步细化网格，以追求更加精确的计算结果，并同时兼顾计算速度。

3 热弹性阻尼与结构参数的关系

为研究内S形柔性梁多环谐振陀螺结构参数对热弹性阻尼的影响，需要找出热弹性阻尼随各结构参数的变化关系。解决这一问题的方法是：改变陀螺有限元模型中各个结构参数的大小，并进行热弹性阻尼的仿真分析，从而计算出QTED随各结构参数的变化曲线。Zener理论表明：对于谐振梁而言，由于弯曲变形产生的热弹性阻尼大小与谐振频率f0密切相关[10]。从图3可以看出，内S形柔性梁多环谐振陀螺的四波腹面内振动模态会导致同心圆环与支撑梁的弯曲变形，从而导致圆环和支撑梁中各区域温度不均匀，这与谐振梁的热弹性阻尼机理类似。因此，内S形柔性梁多环谐振陀螺的热弹性阻尼也可能与f0有着密切联系，本文在计算QTED的同时也计算了f0。

陀螺的初始结构参数取值如表2所示。当研究某一个结构参数对热弹性阻尼的影响时，保持其余结构参数不变。

表2 陀螺的初始结构参数取值Table 2 Initial structure parameter value of gyroscope

嵌套同心圆环作为谐振陀螺的主要组成部分之一，其数目会影响热弹性阻尼，影响结果如图5所示。由图5可知，当N＝3时，QTED最小：当N＞3时，随着N的增加，QTED也随之增加。同时可以发现，f0的变化趋势和QTED的变化趋势相反。为减小热弹性阻尼，应将环数设计为N＞3，且环数越多越好。然而需要注意的是，在其他结构参数不变的情况下，环数越多则同心环之间的间隙越小，当间隙过小时，将受到刻蚀工艺的深宽比限制。因此，在刻蚀深宽比可以达到要求的情况下，N越大越有利于QTED的提升。

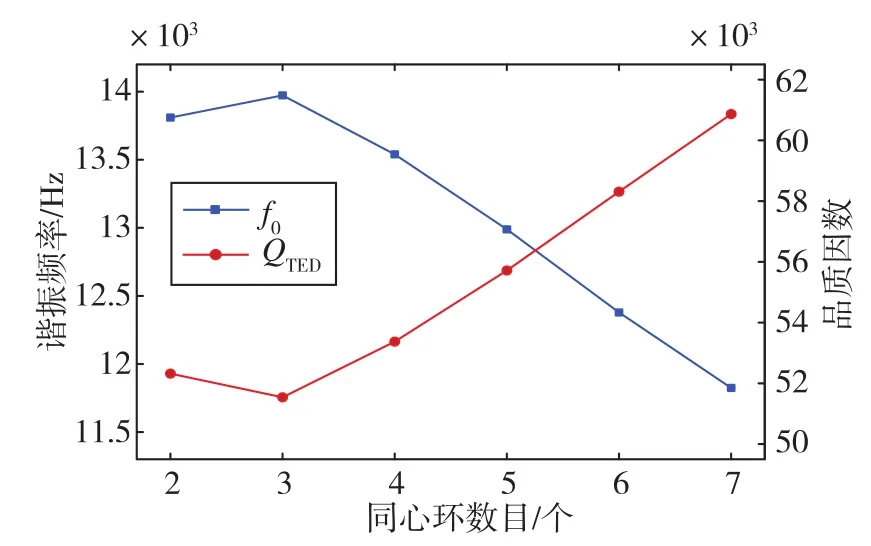
图5 同心环数目对热弹性阻尼的影响Fig.5 Influence of concentric ring number on thermoelastic damping

S梁的弯曲程度、中央圆盘尺寸和谐振器尺寸也是陀螺的重要结构参数，这些结构参数的变化同样会影响热弹性阻尼的大小，影响结果如图6所示。可以发现，受这些结构参数的影响，f0的变化趋势均与QTED的变化趋势相反。计算结果表明，S梁的圆心角α越大，则f0越小，如图6(a)所示。需要注意的是，S梁的应力主要集中在弯曲部分，圆心角α越大，则该部分应力越集中，这将影响陀螺的抗冲击能力。因此，在设计陀螺结构时还需要考虑其抗冲击能力，在保证抗冲击能力达到要求的前提下，α设计得越大越有利于陀螺性能的提升。图6(b)表明，中央圆盘半径r越大，则f0越大，同时QTED越小。这是因为中央圆盘固定在基底上，r越大意味着谐振器被固定的部分更多，从而谐振频率会变大，进一步降低了QTED。 这说明中央圆盘越小越有利于热弹性阻尼的减小，但是设计过小的中央圆盘对于实际工作中的陀螺是不可行的，这是因为当谐振器被固定的部分过小时，谐振状态的可靠性会随之下降。最外层环半径R1对热弹性阻尼的影响如图6(c)所示，R1越大，则f0越小，同时QTED越大。R1直接决定了陀螺的整体大小，由于MEMS器件尺寸的限制，陀螺的尺寸不能过大，这需要在性能和尺寸之间进行权衡。图6(d)为最内层环半径R2对热弹性阻尼的影响，R2越大，则f0越小，同时QTED越大。需要注意的是，在其他参数不变的前提下，最内层环半径越大，同心环之间的间隙越小，这也会受到刻蚀深宽比的限制。

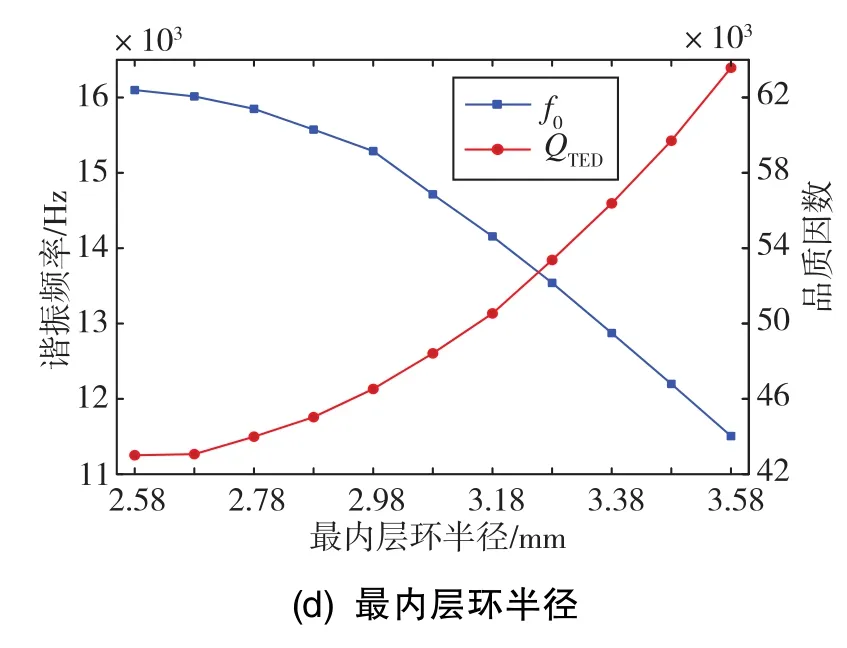
图6 几种结构参数对热弹性阻尼的影响Fig.6 Influence of several structure parameters on thermoelastic damping

同心环宽度W1和支撑梁宽度W2也将对陀螺性能产生影响，影响结果如图7所示。从图7可以看出，W1和W2对f0和QTED的影响类似，越小的宽度可以得到越小的f0和越大的QTED。因此从理论上而言，为获得高QTED的陀螺，应该尽可能减小宽度W1和W2。但是受到微机械制造工艺的限制，过小的W1和W2是不容易实现的，因此在设计同心环宽度和支撑梁宽度时，需要同时考虑制造工艺条件与性能两方面因素。

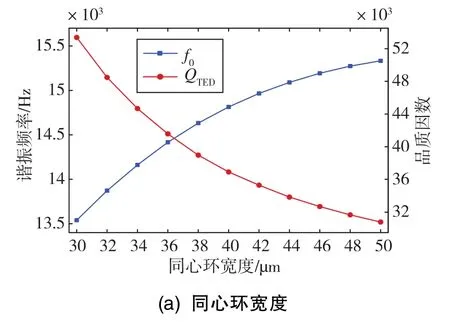
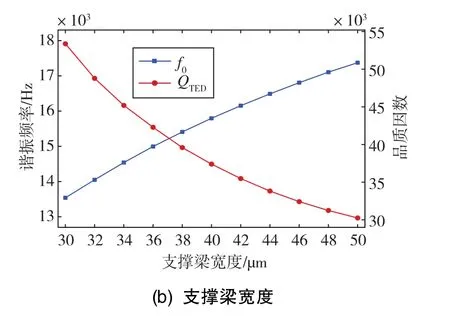
图7 同心环宽度和支撑梁宽度对热弹性阻尼的影响Fig.7 Influence of concentric ring width and support beam width on thermoelastic damping

根据上述结果可知：内S形柔性梁多环谐振陀螺的热弹性阻尼与f0有着密切联系，这与Zener理论很相似。Zener理论表明，对于谐振梁而言，其热弹性阻尼可以由以下公式求出[10]

式(4)、式(5)中，τth为热弛豫时间常数，d为谐振梁弯曲方向的宽度，T0为谐振器工作的初始温度。由式(4)可知，QTED为关于2πf0τth的函数，其函数图形称为 Zener曲线，如图 8所示。当2πf0τth＝1时，QTED取得最小值：当 2πf0τth≪ 1时，谐振器工作在等温状态；当2πf0τth≫1时，谐振器工作在绝热状态。

对于内S形柔性梁多环谐振陀螺而言，其四波腹模态为面内振动，谐振器弯曲方向的宽度d即为同心环和支撑梁的宽度。如图8所示，将不同结构参数下的QTED仿真结果与Zener曲线进行对比。其中，同心环和支撑梁的宽度始终保持相等，以方便确定Zener理论中d的值。对比结果表明，QTED仿真值与Zener曲线的理论值高度吻合，这说明内S形柔性梁多环谐振陀螺的热弹性阻尼可以用Zener理论近似求解。此外，在各个结构参数变化的情况下，内S形柔性梁多环谐振陀螺始终工作于等温状态，这是因为单晶硅具有高的导热系数，从而热弛豫时间常数较小，同时其谐振频率较低，因此满足2πf0τth≪1的条件。根据Zener理论可知，当陀螺工作于等温状态时，要提高QTED应该降低谐振频率或减小热弛豫时间常数(即减小同心环和支撑梁的宽度)，这与图5～图7的仿真结果是一致的。

图8 QTED仿真值与Zener理论的对比Fig.8 Comparison of QTEDsimulation values with Zener's theory

4 结论

本文使用有限元方法分析了内S形柔性梁多环谐振陀螺各个结构参数对热弹性阻尼的影响，对于设计高品质因数的陀螺具有重要指导作用。结果表明，四波腹模态下内S形柔性梁多环谐振陀螺的热弹性阻尼与谐振频率有着密切联系，为了实现低热弹性阻尼和高品质因数，应该设计低谐振频率的陀螺。同时，设计高品质因数的陀螺结构还需要综合考虑微机械制造工艺的条件、陀螺封装尺寸、陀螺稳定性、抗冲击能力等因素。在这些条件都满足要求的情况下，应该增加同心环数目(N＞3)、增大S形支撑梁的圆心角、增大最内层环和最外层环的半径、减小中央圆盘的尺寸、减小支撑梁和同心环的宽度。此外，不同结构参数下QTED仿真值与Zener理论的对比结果表明，内S形柔性梁多环谐振陀螺的热弹性阻尼也可以用Zener理论来描述，这对于研究内S形柔性梁多环谐振陀螺的热弹性阻尼机制有着重要意义。