基于大气偏振光的载体姿态参数提取方法

任建斌，杨 明，宋 妮

(中北大学理学院，太原030051)

0 引言

大气偏振光包含着与太阳方位有关的丰富信息，自然界中一些具有偏振感知特性的生物如沙蚁、蜜蜂、蝗虫等都能通过检测天空部分区域的偏振光信息去推知太阳位置并借以实现精准导航[1-2]。虽然人眼不能直接感知天空偏振光，但借助于一些特殊装置，也可以观察到天空光的偏振特性。例如，当人们透过线偏振片观察天空光时，随着偏振片的转动，光线呈现出明暗变化的规律，这表明天空分布着大量的偏振光。考古研究还发现，古代维京人航海时，在太阳不可见的情况下，能借助于一种叫 “太阳石”的薄片，通过观察天空光明暗变化的规律去推知太阳的方位信息并实现海上航行[3]。

人们通过对沙蚁、蜜蜂等膜翅目昆虫的行为学和电生理学研究，基本揭示了这些昆虫利用偏振光导航的生物机理。它们通过复眼背部边缘区具有偏振感知功能的单眼检测来自天空不同方向的偏振光信息(主要是E-矢量信息)，利用这些信息去推算太阳子午线(太阳方位角)与体轴的夹角，并通过千百万年进化的生物钟补偿太阳位置变化所引起的导航偏差，使其能在外出觅食或远距离迁徙等活动中保持精准导航[4]。2000年，Lambrinos等[5]在对昆虫的电生理学研究的基础上利用紫光滤波片、线偏振片和光电二极管搭建出仿生偏振光传感器并将之应用于机器人Sahabot的导航实验中，进一步验证了偏振光导航的机理。

随着研究的进一步深入，人们不再满足于仅利用偏振光去推知太阳方位与载体体轴之间的简单关系来实现二维导航及定位，而是试图借助于现代导航理论去探寻大气偏振模式的结构信息并构建这种结构信息与载体空间姿态变化之间的动态关系[6]。生物学家通过对沙蚁设置特殊的行动路径进行研究，进一步的研究还表明，这些昆虫外出觅食时，在路径有较大起伏变化的情况下仍能准确归巢，说明大气偏振模式不仅可以提供二维的航向信息，也可在身体姿态发生变化的情况下通过偏振信息获取自身姿态参数，实现三维导航[7]。这些研究为偏振光导航的全面应用提供了广泛的生物学依据。在此基础上，研究者已经给出了多种利用大气偏振模式获取载体空间姿态的直接方法[8-9]或辅助的组合导航方法[10-11]。

本文在这些方法的基础上提出了一种利用大气偏振光的E-矢量模式信息获取载体姿态的最小二乘方法，该方法将载体当前状态下的E-矢量模式与参考坐标系下的E-矢量模式进行匹配，利用误差最小原理构建确定姿态矩阵的优化问题，借助于奇异值分解的方法[12]确定出载体空间姿态。

1 大气偏振模式的刻画及检测

1.1 理论大气偏振模式

进入大气层的太阳光一部分会受到空气分子、气溶胶粒子等的散射作用产生偏振现象，即光的电场矢量(E-矢量)由原来的自然振动状态变为仅沿某一特定方向振动的偏振状态，形成了偏振光，如图1所示。这种偏振光主要是线偏振光，用偏振度和偏振角刻画。偏振度是测量点处偏振光光强占总光强的比例，偏振角是该点处的E-矢量振动方向与当地子午线之间的夹角。

图1 Rayleigh单次散射原理Fig.1 Principle of Rayleigh single-scattering

根据Rayleigh散射相关理论，在入射光为自然光的情况下，天空某点处的偏振度与该点到太阳方向的角距有关[13]，其计算公式为

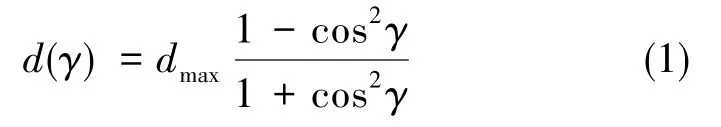
式(1)中，γ为散射角。理论上，天空最大偏振度dmax＝100%，但实际中由于分子的多次散射及尺寸较大的气溶胶离子的米散射作用以及地面反射偏振光等因素的综合影响，该值会有偏差，低于理论值，但每个点处的E-矢量基本保持不变，具有一定的稳定性。

将上述单次粒子散射的Rayleigh模型推广到空间中，建立基于Rayleigh散射原理的球面表示。当太阳空间位置为(hs，φs)时，偏振角为

式(2)中，hs为太阳高度角，hp为观测点高度角，φ为观测点到太阳子午线的角距。

天空每个测量点处的偏振度和偏振角各不相同，但整体上保持着稳定的分布形式，它们分别以太阳和太阳子午线为中心，形成一种对称分布的模式。其中，偏振度以太阳为中心呈中心对称分布，太阳方向偏振度为零。随着散射角逐渐增大，偏振度也逐渐增大，在距离太阳角距为90°的地方达到最大，形成一条最大偏振度线，其后随着角距进一步增加，偏振度逐渐减小。天空中大量偏振光与自然光相互叠加形成的这种稳定分布的模式被称为大气偏振模式，主要由偏振度模式和偏振角模式表征，如图2所示，短线的粗细表示偏振度的大小，其切向即为该点处的E-矢量方向。

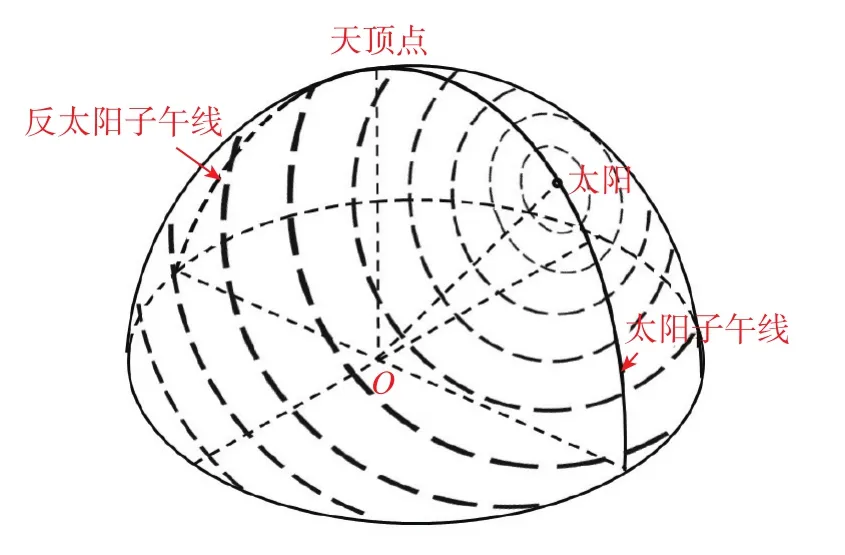
图2 大气偏振模式示意图Fig.2 Schematic diagram of atmospheric polarization pattern

为了方便后面表示，本文在球面坐标系的基础上引入东-北-天空间直角坐标系作为地面参考系，即取地面参考点为坐标原点，X轴沿当地纬线指向正东，Y轴沿当地子午线指向正北，Z轴垂直向上指向天顶，如图3所示。

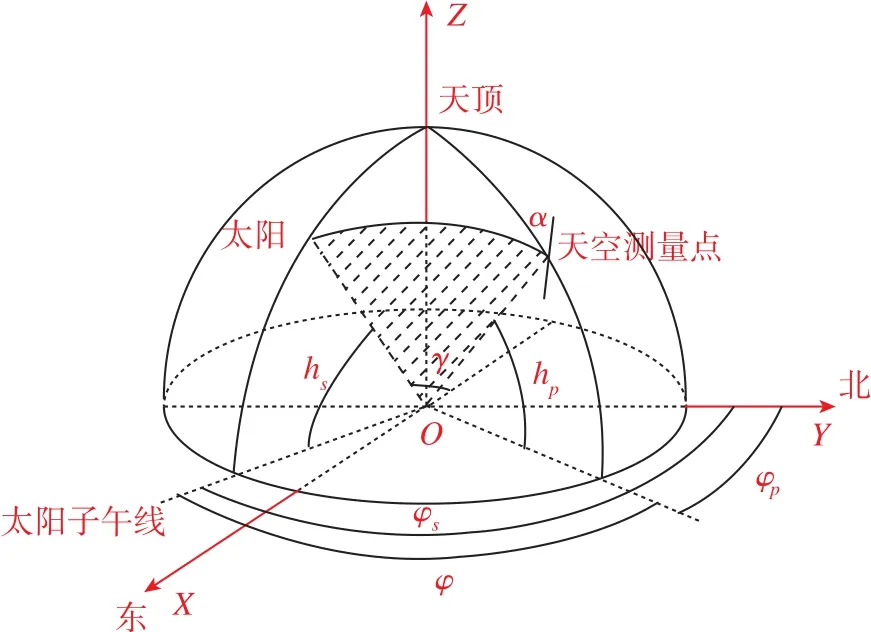
图3 天球坐标系各点位置示意图Fig.3 Schematic diagram of points in celestial coordinate system

在天球坐标系中，每个点处的E-矢量总是垂直于过太阳、测量点和地面观测点所构成的三角平面，根据球面三角的余弦定理，有

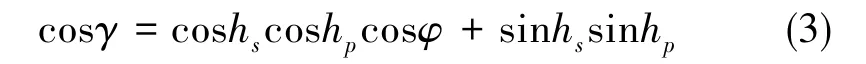
对于天空每个测量点p(hp，φp)，该点处的E-矢量可由下面的单位矢量表示[14]

对于每个空间测量点，都有一个确定的偏振度值和E-矢量值。虽然有的测量点处这些值会有相同，但整体上看，由于偏振度和E-矢量具有稳定的模式特征，在载体姿态发生变化时，机载偏振光传感器所测量的偏振模式与参考系下的偏振模式不同，但只是空间位置上的偏转，即可看作是沿某个空间矢量旋转一定角度得来的。如果能将两种状态下的偏振模式在误差最小的情况下进行最优匹配，也就找到了从载体坐标系到参考系的偏转角度，即姿态角。

1.2 大气偏振模式实测

图像法是大气偏振光测量及偏振模式重建的重要方法，被广泛应用于大气遥感、监测等领域。该方法利用单反相机加装鱼眼镜头和线偏振片，可实现天空180°大范围内偏振信息的测量。通过偏振片检偏，电场矢量振动方向与偏振片透光轴一致的偏振光通过，而其他方向的偏振信息被抑制。鱼眼镜头将全天域不同方向的检测点投射到二维成像面上，通过CCD响应将光强信息转化为图像灰度信息，每个成像点对应一个方向的偏振信息。对于每个测量点，设置偏振片透光轴方向和像平面基准方向三次不同角度的测量，或搭建三组可实现同步测量，可解算出全天域内每个方向的偏振信息。检测原理如图4所示。

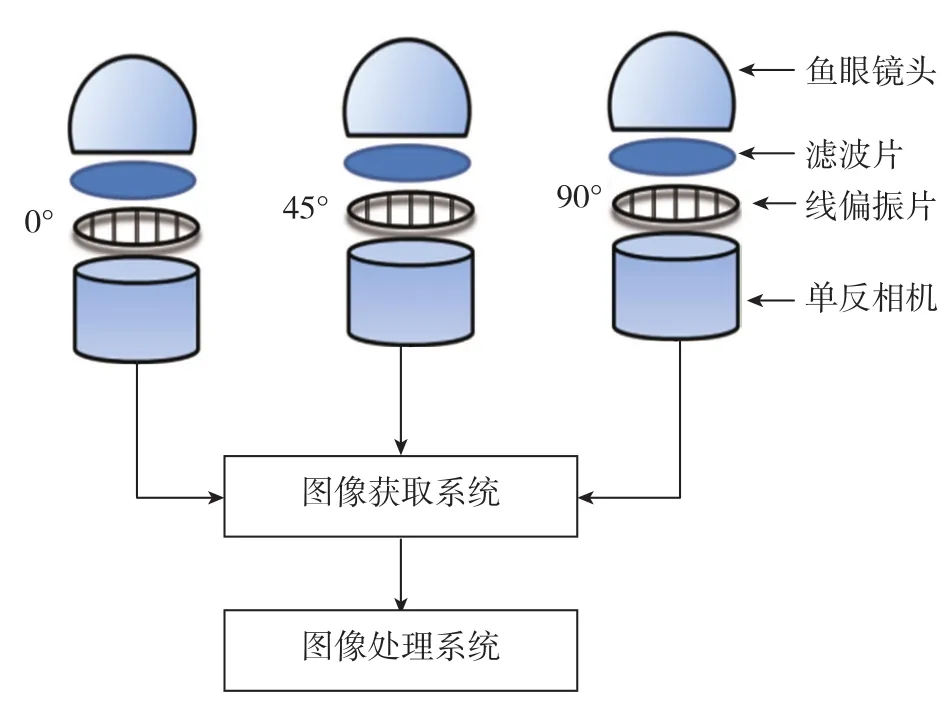
图4 图像法偏振检测原理Fig.4 Polarization detection principle with imaging method

如图5所示，测量平台包括鱼眼镜头、偏振片、滤波片、单反相机和计算机等部分。镜头选用适马EX DC 4.5mm f2.8鱼眼镜头，可覆盖180°视场范围内的整个天空，实现全天域偏振信息的同步采集。偏振片选用Thorlabs公司的线偏振薄膜LPVISE2X2，消光比大于1000：1，可将其视为理想的偏振元件。利用光学平台和精密光学位移台将检偏通道中三个偏振片的透光轴与基准轴夹角分别设置为0°、45°和90°，并利用偏振分析仪(型号：Thorlabs PAX5710VSI)进行校准，以保证偏振片安装角度的高精度。单反相机将光强度值转化为图像灰度值，然后利用计算机进行图像处理。若以I0、45和I90分别表示这三个方向上检测到的光强，则该方向上的偏振信息可由以下公式解算：

图5 偏振成像检测系统Fig.5 Diagram of polarization imaging detection system

再通过鱼眼镜头空间位置相对于成像平面的几何标定[15]，可重建出大气偏振的E-矢量模式和偏振度模式。

在测量日的上午八点到下午六点时段，随机选择一个整点时刻对全天域进行拍摄。检测时间段内，天气晴朗，能见度20km左右，云量小于5%，光学厚度0.283，空气质量指数(AQI)63，平均PM2.5浓度为26(单位：μg／m3)，符合Rayleigh散射的条件。测量时，先调整水平仪使云台保持水平，然后利用指南针校准云台，并在线磁偏角查询(网址：http：／／www.magnetic-declination.com／)进行补偿，使其零点对准地平面坐标系下的正北方向，最后旋转云台到指定的角度对天空进行连续拍摄。拍摄完成后，再通过Photoshop和Matlab软件对原始图片进行处理，获得每个测量时刻的偏振信息。处理结果如图6所示，其中，第一行是相机所拍摄的原图，第二行、第三行分别是计算机重建的偏振角模式与偏振度模式。可以看出，其对称性分布和理论模式基本相同。

图6 图像法测量的大气偏振模式Fig.6 Atmospheric polarization pattern measured by imaging method

1.3 太阳方位角信息提取

在E-矢量的空间表示中，需要用到实时太阳方位信息，本文通过获取到的偏振度数据利用聚类分析的方法可以解算出载体当前模式下的太阳方位角。根据前面的分析，太阳位置的偏振度为零，并且偏振度随着空间位置(散射角逐渐增大)以同心圆的方式渐增，在与太阳角距90°的位置达到最大(最大偏振度线)。本文选取偏振度在某一区间的数据点pi＝(θi，φi)作为聚类的对象，对所对应数据点的高度角θi和方位角φi进行聚类(i＝1，2，…，N)，求取类中心。具体过程如下：

初始化：给定聚类类别数N，设定迭代停止阈值ε，指定位置初值分别为任选的高度角和方位角。

步骤1：计算第i个数据点xi到第v类中心pv的距离(为适合的矩阵范数)

式(8)中，上标j表示迭代次数。

步骤2：更新划分矩阵U(j)中的元素

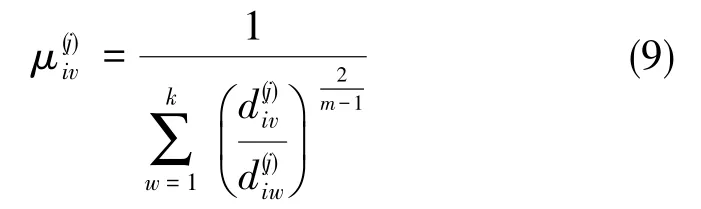
式(9)中，m∈[1，＋∞)为平滑因子。

步骤3：更新聚类原型矩阵P(j)中的元素

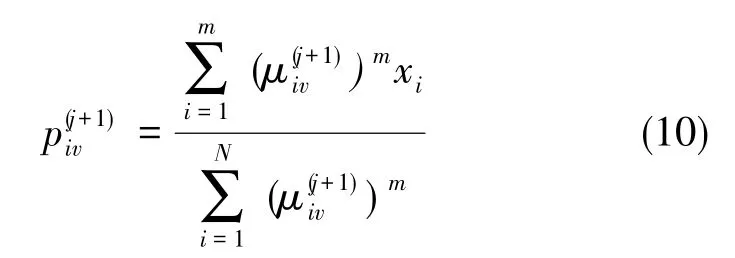
图7 太阳方位角聚类拟合结果Fig.7 Cluster fitting results of solar azimuth

2 基于E-矢量模式的导航算法

2.1 姿态变换矩阵

从数学的角度讲，姿态就是载体运行过程中其固联坐标系(体坐标系)与地面坐标系(参考系)之间的转动关系，体现为两组坐标系之间的变换矩阵或方向余弦矩阵。确定该矩阵的一种重要方法是利用一组不相关的空间矢量在两组坐标系下的位置变换信息反推姿态变换矩阵。导航应用中，一般选取有明显特征的矢量，如太阳、恒星体、地磁场等。在偏振模式下，天空的矢量特征点很多且非常显著，利用机载的偏振光传感器追踪这些偏振矢量特征点的变换过程，可获取相应的姿态变换矩阵和载体姿态。

载体坐标系与偏振传感器固联，原点o选在质心处，x轴取为横轴，向右为正，y轴取为纵轴，向前为正，分别与相平面的xoy坐标系一致，z轴垂直向上，与传感器光轴一致，满足右手规则。姿态角表示地面参考系(a系)与载体坐标系(b系)之间的转动关系，若以ϑ、ψ和ϕ分别表示俯仰角、偏航角和滚转角，则两组坐标系间的变换矩阵为[8]

若能求得变换矩阵，则可根据其部分元素求取姿态角，即

式(12)～式(14)中，cij(i，j＝1， 2， 3)为变换矩阵中第i行第j列位置的元素。

为方便论述，同一方向上的E-矢量在地面参考系和载体坐标系下分别用ri和bi表示。其中，i＝1，2，…，n，n为测量点的数目。本文的目的是通过检测天空偏振光的E-矢量模式从载体系到参考系变化过程中获取载体的姿态变换矩阵C(或方向余弦矩阵)，使得

2.2 基于E-矢量的姿态解算

3 实验仿真

为了验证本文方法的有效性，建立了一个模拟的飞行器控制台来验证文中所提的姿态解算方法，如图8所示。以外部大球面表示地面观测点检测到的偏振模式，与地面参考系固连，用内部小球面表示飞行器所检测到的偏振模式，与体坐标系固连。当载体无姿态变化时，体坐标系三轴方向与地面参考系三轴方向一致，E-矢量在两组坐标系下的坐标相同。当载体姿态发生变化时(载体偏转)，机载偏振光传感器所检测到的E-矢量模式随其姿态变化而变化，转过的角度即为所模拟的飞行器姿态变化的大小，通过与载体实际转动的角度相比，可以分析出算法误差的变化情况。

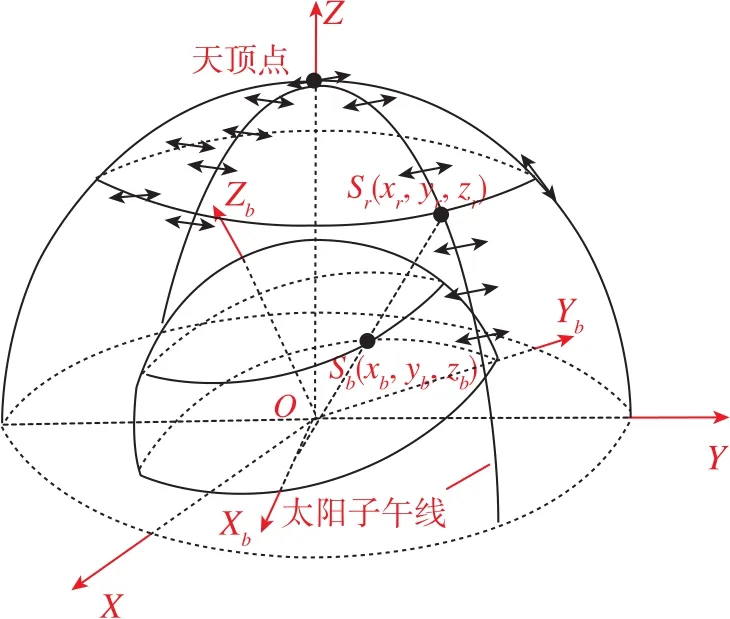
图8 模拟飞行器控制台Fig.8 Diagram of simulative vehicle console

观测点地理坐标为北纬 37°54′、东经 112°33′，观测时间为2020年4月25日上午8：00至下午18：00的连续时间段内。先将相机坐标系(体坐标系)与地面参考系保持一致，将获取到的偏振模式作为地面坐标系参考基准，然后让相机随载体转动，通过相机拍摄天空偏振灰度图，利用Matlab软件经过处理获取到该时段内的偏振E-矢量模式，通过预设载体姿态变化数值，利用其E-矢量在地面参考系和载体坐标系下两组坐标变化，求取变换矩阵并反解出对应的姿态角数值，两相对比，验证算法的正确性和稳定性。

图9、图10给出了动态模拟结果。图9为理论值与计算结果随时间变化的对比图，模拟飞行器偏航角ψ从－180°～180°变化，俯仰角ϑ和滚转角ϕ均从－90°～90°变化，可以看出姿态角预设值与解算值吻合非常好。图10为三轴姿态的解算误差随时间变化的结果图，三个解算角度的最大偏差分别为 0.41°、0.50°和 0.49°，整个模拟时段(300s)的均方根误差分别为 0.0741°、0.0932°和0.0943°，说明所给利用偏振E-矢量模式变化的载体姿态解算算法具有较好的稳定性。

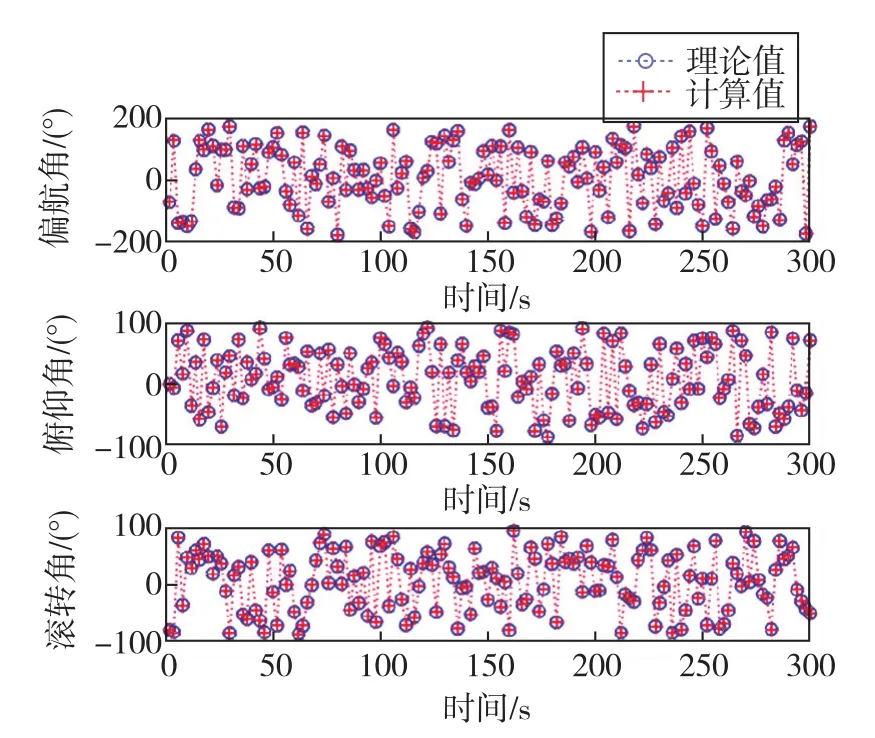
图9 姿态角随时间变化曲线Fig.9 Curves of attitude angle with time

图10 姿态角解算误差随时间变化曲线Fig.10 Curves of attitude angle calculation error with time

将姿态角的实际测量值与理论值进行比较，发现误差小于0.1°的数据占68%，误差在0.1°～0.4°之间的数据占21%，误差大于0.4°的数据占11%。因此，从这些实验统计数据中可以看出，姿态角的解算误差在0.5°以内。造成误差的主要原因是载体姿态变化过大时，不可避免地受到地面反射偏振光的影响，使得所获取到得的E-矢量数据与地面参考模式相应区域的E-矢量数据相比，偏差有所增大，使得解算的姿态误差增加，可通过提高偏振模式检测质量予以降低。

最后，进一步分析了测量当天利用大气偏振模式解算姿态角的误差随时间变化情况，每隔半小时采样计算一次，给出了姿态解算误差随时间变化的曲线图，如图11所示。从整体看，解算误差随时间小幅发散，主要原因是测量过程中太阳光照强度、散射粒子属性以及人类活动影响等因素不断变化引起米散射现象，使得偏振模式的对称性受到影响。但这些影响因素相对于气象条件来说微不足道，在短时间内不会对导航精度产生较大影响。从图11中可以看出，三个角度的解算误差均小于0.2°，说明利用大气偏振模式进行导航具有一定的时间稳定性。

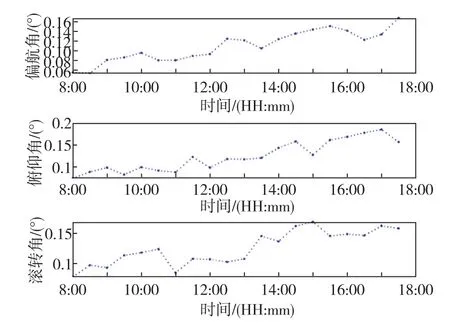
图11 姿态角随测量时间变化曲线Fig.11 Curves of attitude angle with measurement time

4 结论

本文提出了一种利用大气偏振模式获取载体空间姿态的直接方法。首先，在Rayleigh单次散射模型的基础上获取了大气偏振的E-矢量模式并分析了它与天空测量点空间位置相对应的结构特征。然后，利用加装鱼眼镜头的单反相机和偏振片搭建了偏振模式的测量平台，模仿昆虫偏振感知功能进行测偏，通过图像处理获得了大气偏振模式的实测数据，在数据处理中根据偏振模式的对称性特点，引入聚类分析的方法提取了太阳方位角信息并进一步建立E-矢量模式。最后，给出了一种利用E-矢量模式获取载体空间姿态的算法，将载体系下获取的E-矢量模式与参考系下的E-矢量模式进行最优匹配，利用偏振模式的结构性特点获取到其背后每个测量点空间位置矢量的转动关系，利用奇异值分解的方法求取姿态变换矩阵，以此来确定姿态。仿真实验利用模拟飞行器控制台进行验证，通过预设姿态角度并和偏振信息解算值相比，三个姿态角的最大偏差不超过0.5°，说明本文方法具有较好的稳定性。文中在验证方法的有效性时，只考虑了全天域偏振模式的空间匹配，但实际导航中，当载体姿态发生变化时，其上搭载的偏振光传感器不可避免地会获取到地面反射产生的偏振光，使得有效的天空区域面积减小，如何从中将有效的天空区域分割出来并与参考系下的全天域模式中对应的部分进行匹配，是该方法进一步推广应用的关键。