基于惯性／航迹推测的煤矿掘锚机组合导航方法

伦华江，徐 枫，黄 喆，许东旭，张晓日

(1.中国航天科技集团有限公司物联网技术应用研究院，北京100094；2.力信测量(上海）有限公司，上海201300；3.天津科技大学电子信息与自动化学院，天津300222)

0 引言

煤炭是我国主体能源，在我国能源消费总量中占比60%[1]。煤炭的获取依赖于安全开采[2]，而实现工作面安全开采离不开先进、可靠的掘进装备[3]，其中掘锚机因其掘进速度快、安全性好和巷道成形效率高等特点而广泛应用于我国矿井煤巷施工中[4-5]。煤矿巷道中使用激光指示和人工观察相结合的方法来指导掘进，但这种方法劳动强度大，工人安全得不到有效保障，极大降低了施工质量和掘进效率。因此，研究高可靠性、高精度的导航定位方法在掘锚机煤巷施工中具有很高的工程应用价值。

近年来，国内学者在煤矿掘进机导航定位方面取得了较多研究成果。王以忠等[6]提出了一种基于空间矢量约束的实时位姿组合测量方法，通过构建空间四边形的方式实现了煤矿掘进机的六自由度测量，但是该方法不能解算空间四边形中有两边平行的特殊情况。田原[7-8]基于四点式光靶的掘进机定位方法实现了机器视觉和惯性的组合导航，但该方法在巷道进尺方向精度较差。而后该学者从掘进机特点出发，提出了一种基于零速修正的掘进机惯性导航定位方法，解决了环境适应性差、惯性导航长时定位精度低等问题。薛光辉等[9]针对惯导误差累积的特点提出了一种基于激光靶向跟踪的掘进机位姿测量方法，可以在标靶单点布站的情况下完成掘进机所有位姿参数的测量，但该方法受限于煤尘问题，不能长距离使用。就目前技术而言，由于掘进机工作环境复杂，基于单一传感器的导航定位技术存在局限性，多传感多信息融合的导航技术更有希望解决掘进机的导航定位问题[10]。文献[11]～文献[15]进行了里程计＋捷联惯导组合导航技术在管道、自动驾驶及井下车辆等场景中的应用研究。掘进机定位技术关键在于建立掘进机的实时坐标[16]，然而上述文献中未给出载体坐标的解算方法。基于零位测量实时更新载体坐标和姿态的方法在盾构导向中应用比较成熟[17]，其基于载体与传感器之间的刚体关系，在已知传感器坐标和姿态角的情况下实时解算载体坐标。

为了实现掘锚机定位测量和掘进导向，进一步丰富导航参数，本文基于对现有的技术研究，提出了基于惯性／航迹推测的组合导航方法。通过对惯导实时位姿测量，结合掘锚机刚体零位标定数据、全站仪测量数据和计划线数据等，解算出掘锚机实时坐标及导向参数，实现了精确导向功能。

1 定位和偏差算法

1.1 坐标系定义

位姿测量系统坐标系的定义如图1所示。OnXnYnZn(简称n系)为参考坐标系，OnXn轴指向正东方向，OnYn轴指向正北方向(方位角为零度的方向)，OnZn轴垂直向上，原点由城市规划设计部门设定；ObXbYbZb(简称b系)为掘锚机坐标系，原点位于机体中线上，ObXb轴指向机体右侧，ObYb轴由机尾指向机头，ObZb轴满足正交坐标右手系；OmXmYmZm(简称m系)为惯性测量单元(Inertial Measurement Unit，IMU)坐标系，原点在 IMU中心，坐标轴为IMU自身出厂的坐标轴。

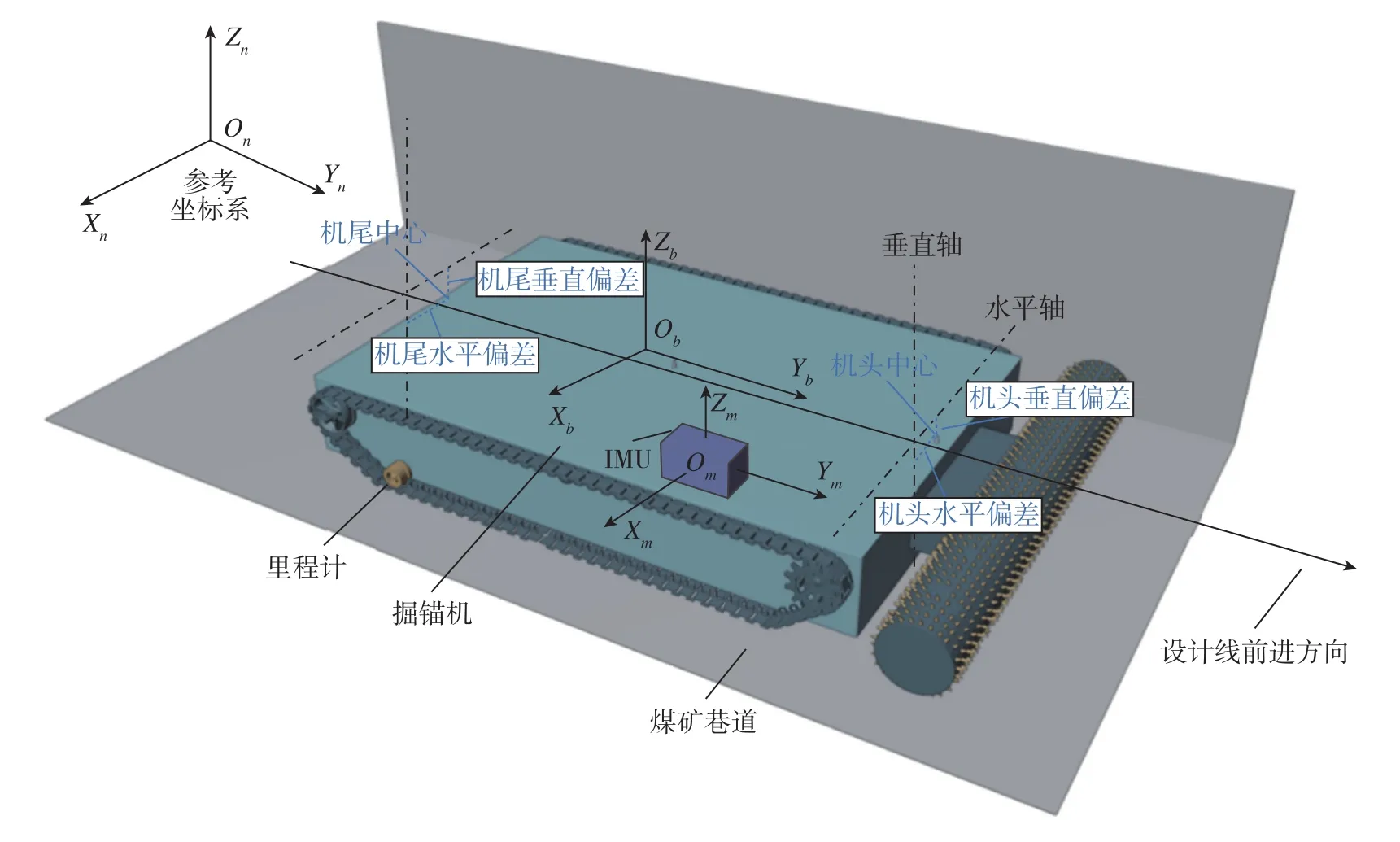
图1 测量系统坐标系定义及掘锚机与设计轴线空间位置关系Fig.1 Definition of the measurement system coordinate system and spatial position relationship between the roadheader and the design line

在掘锚机施工阶段，进行测量的主要任务是获取导向参数，即测量机体与计划线的偏差量，从而控制机器前进方向。图1描述了掘锚机与设计轴线在空间中的位置关系，过机头中心点和机尾中心点分别做垂线垂直于设计轴线，则垂线段在水平面上的投影为水平偏移量，在竖直面上的投影为垂直偏移量。始终将水平偏差和垂直偏差控制在规定的范围，就可以使掘锚机沿着计划线前进，获得良好的直线度。

为了求解掘锚机相对于计划轴线的绝对位置偏差，需要实时解算机头中心点和机尾中心点的坐标，然后根据点与直线的相对位置关系计算偏差量。解算的数据流程图如图2所示，主要分三步来实现偏差量计算：

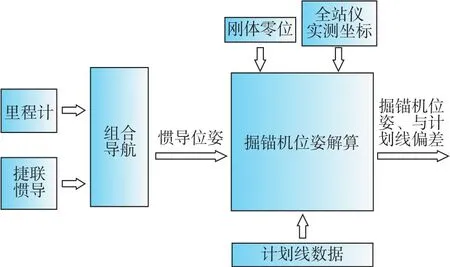
图2 数据流程示意图Fig.2 Flowchart of data

第一步为零位标定，即确定掘锚机与IMU之间的相对位置关系和姿态关系。其中，位置关系通过标定机头中心点和机尾中心点在n系下的坐标确定，姿态关系通过标定b系和m系的旋转矩阵确定。

第二步为坐标解算，即根据里程计和IMU获取机头中心点和机尾中心点在n系下的坐标。

第三步为偏差计算，即根据空间中点到直线最短距离原理计算水平和垂直偏差值。

1.2 零位标定

在零位处获取机尾、机头和IMU在n系下的坐标Pa0、Pb0和P0，由IMU解算出自身三个姿态角，即俯仰角α0、横滚角β0和航向角γ0。 则可得机尾、机头在m系下的坐标Qa0和Qb0，表达式如下

由于IMU与掘锚机是刚性连接的，所以在以后的机体运动过程中，Qa0、Qb0以及保持不变。

1.3 坐标解算

分两个步骤进行求解：1)基于里程计测量的位移数据和姿态信息计算IMU实时坐标；2)结合IMU实时姿态角数据和零位数据计算机头机尾实时坐标。

在掘锚机运动过程中，里程计输出空间位移数据，给定初始位置，可以推算实时位置信息。设里程计第i采样间隔的里程增量在b系下的矢量表示为ΔSbi， IMU姿态角构成的旋转矩阵为，根据航位推算原理，IMU实时坐标可表示为[19-20]

式(5)中，Pat为机尾中心在n系下的坐标，Pbt为机头中心在n系下的坐标。

1.4 偏差计算

机尾、机头偏差量求解原理如图3所示。将掘锚机机尾中心A和机头中心B在平面XnOnYn和平面ZnOnYn投影， 得到投影点A′、A″、B′和B″，将设计轴线起点C和终点D在平面XnOnYn和平面ZnOnYn投影， 得到投影点C′、C″、D′和D″， 平面A′AA″交线段CD、C′D′和C″D″于点E、E′和E″，平面B′BB″交线段CD、C′D′和C″D″于点F、F′和F″。则按照本文偏差量的定义，A′E′即为机尾中心点水平偏差量，A″E″为机尾中心点垂直偏差量，B′F′为机头中心点水平偏差量，B″F″为机头中心点垂直偏差量。

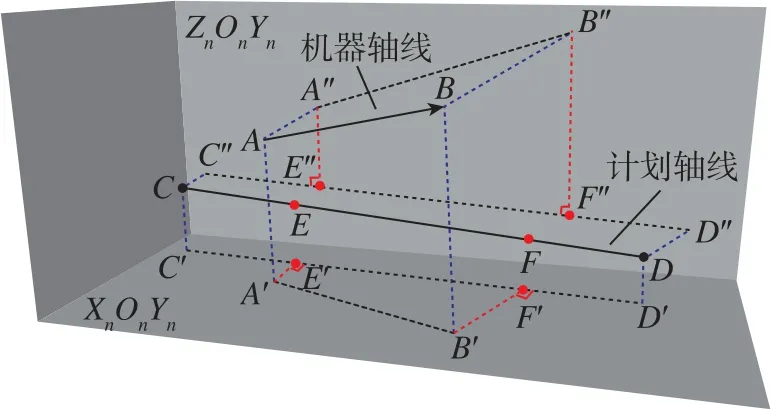
图3 机尾、机头偏差量求解原理Fig.3 Principle of solving the deviation of the tail and head

根据空间点与直线的位置关系[21]，容易得到

计划线起点和终点在n系下坐标已知，记为C(xc，yc，zc)和D(xd，yd，zd)， 则可得C′(xc，yc，0)、C″(0，yc，zc)、D′(xd，yd， 0)、D″(0，yd，zd)。掘锚机机头、 机尾坐标可由式求出，记为A(xa，ya，za) 和B(xb，yb，zb)，则可 得A′(xa，ya， 0)、A″(0，ya，za)、B′(xb，yb， 0)、B″(0，yb，zb)。 将上述点坐标带入式(6)，得到

2 导航系统实验

为了验证组合导航方法的准确性，将惯性测量单元(IMU)和里程计安装在移动小车上进行实验，实验原理如图4所示。

图4 实验原理Fig.4 Diagram of experiment principle

让测试小车沿着设定好的计划线前进，在小车运行到观察位置点时，用全站仪测量小车位置，同时记录惯导＋里程计组合导航系统的定位坐标。结合初始零位及计划线参数，计算机头、机尾在水平方向和竖直方向上的偏移量，通过比较解算值和实测值，获得系统测量误差。本次实验所用的设备如表1所示。

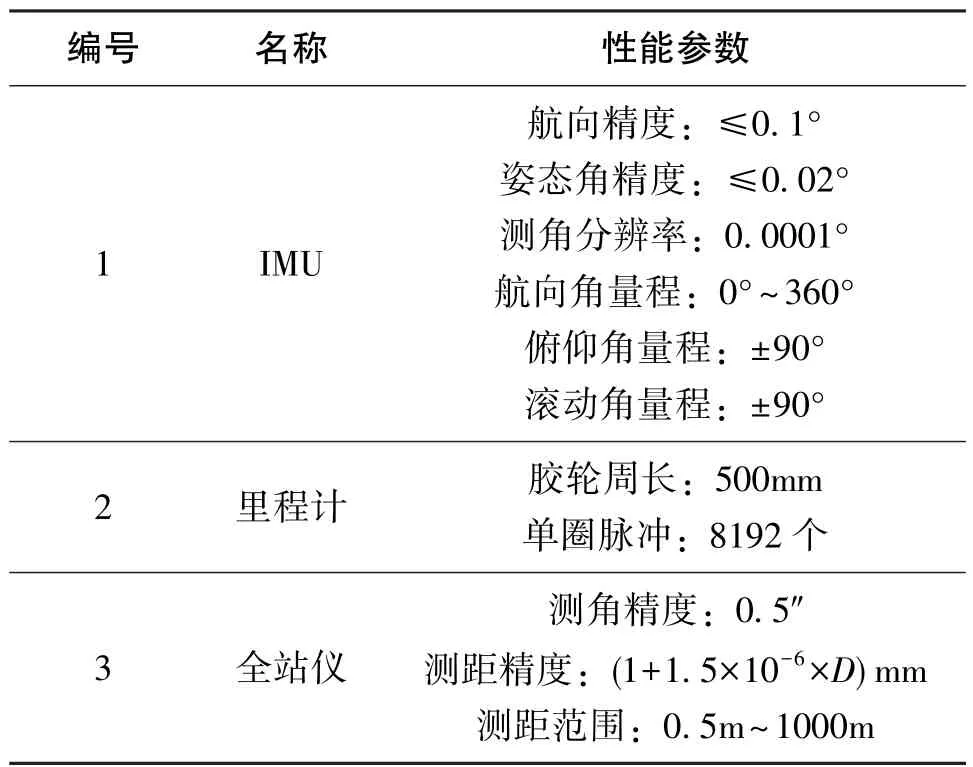
表1 实验设备Table 1 List of experiment apparatus

实验步骤如下：

1)组装实验装置和搭建实验环境。采用铝合金型材、行走轮组装成测试小车主体；在里程计上加装计米轮并通过安装支架固连到车体尾部，其中安装支架中带弹簧机构保证计米轮贴地；在IMU上加装反射棱镜，并通过螺丝固连到车体的右前部位；将全站仪架设在视野宽阔的位置，调平并设站定向。实验装置和实验环境如图5所示。

图5 实验装置与实验环境Fig.5 Diagram of experiment devices and experiment environment

2)标定刚体零位和初始化线路数据。通过全站仪测量小车上的特征点以及陀螺特征点坐标，得到零位坐标数据和零位姿态数据，如表2、表3所示。根据小车运动范围设定沿正北方向150m为前进轴线，得到计划线参数，如表4所示。

表2 零位坐标数据Table 2 Data of coordinate at zero-position

表3 零位姿态数据Table 3 Data of attitude angle at zero-position

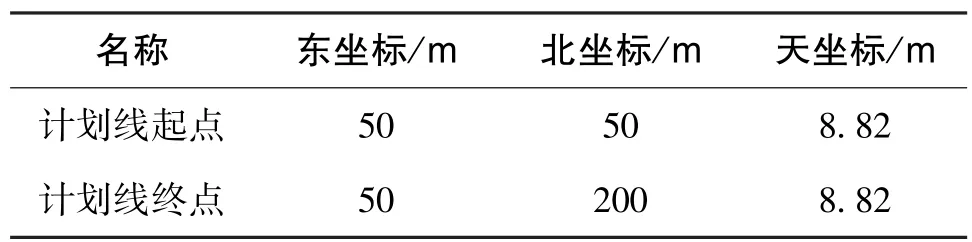
表4 计划线数据Table 4 Data of design line

3)根据安装偏差校准算法[19]获取补偿误差：航向角偏差为0.196°，俯仰角偏差为－0.002°，并补偿到零位的安装偏差中。

4)推动小车向前移动，每间隔约2m用全站仪测量惯导特征点坐标，同时记录惯导自身解算坐标，得到的IMU轨迹如图6所示。通过零位关系求解移动小车上机头、机尾点与计划线的偏差，结合全站仪测量得到的偏差计算误差，得到的偏差变化曲线和误差曲线如图7所示。

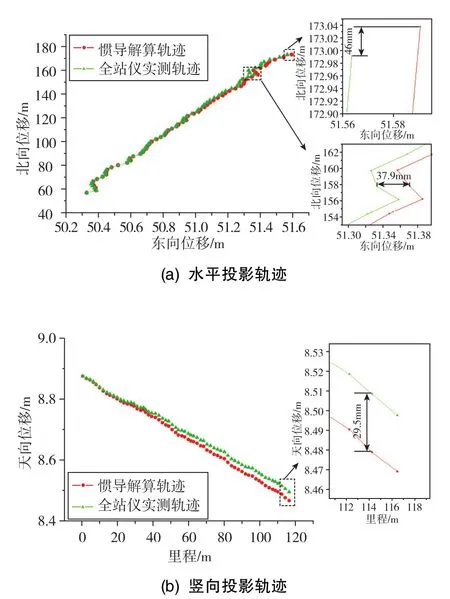
图6 惯导定位轨迹与全站仪定位轨迹比较Fig.6 Comparison between inertial navigation positioning track and total station positioning track

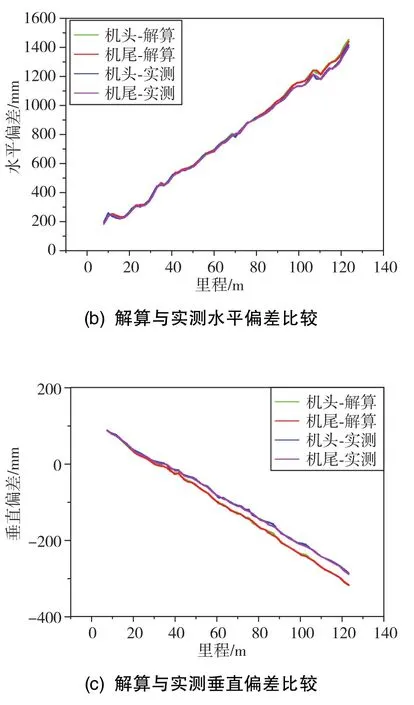
图7 解算与实测偏差对比及误差曲线Fig.7 Comparison of calculated and measured deviations and error curves

由图6可知，小车在前进过程中，北向和东向位移增大，天向位移逐渐减小，对比全站仪测量坐标和惯导解算坐标，两者的变化趋势一致。但随着时间和距离的变化，误差逐渐增大，在东北天方向的最大定位误差分别为37.9mm、46.0mm和29.5mm。在图7的解算与实测偏差比较曲线中，机头机尾中心与计划线偏移量随着里程变化逐渐增大，且头尾变化保持一致。从解算误差曲线图中可以发现，误差随着时间和距离变化累积，在里程108.6481m处，水平方向上机头中心和机尾中心的偏差量误差分别为－44mm和－44mm，在里程114.2266m处，竖直方向上机头中心和机尾中心的偏差量误差分别为32mm和30mm，如表5所示。

表5 实验小车与计划线偏差的最大测量误差Table 5 Maximum measurement error of the deviation between the experiment car and the design line

本次实验中，由于在组装时行走轮与机身轴线有偏角，加之推行小车的力位于小车左后方，小车并没有完全沿着预定的计划线前进，而是朝北偏东方向前进，所以小车在前进过程中东坐标和北坐标逐渐增大，且机头机尾中心向右偏离计划线；计划线设定在高程为8.82m的水平面上，而实际小车下坡前进，故机头机尾中心向下偏离计划线。此外，由于惯性系统存在累积误差，全站仪实测值与组合导航系统解算值之间存在误差，直接体现在惯导定位误差中，间接影响测试小车机头机尾偏离计划线的解算误差。

该组合导航系统的现场应用如图8所示，先在厂里做完零位标定，待掘进装备运到施工现场后做零位复测。某煤矿应用中，巷道长度约300m，掘进过程中对机头水平偏差解算误差进行验证，在同一掘进里程下使用全站仪人工测量机头与设计线的水平偏差，记录测量系统解算的机头水平偏差，并统一编号作对比。表6为掘进里程位于122m～127m区间内的三组人工复核数据和测量系统解算数据。可由表6知，比对误差在130mm以内，满足应用需求。

图8 测量系统现场应用Fig.8 Field application of measurement system

表6 机头中心水平偏差实测值与计算值比较Table 6 Comparison of measured value and calculated value of head center horizontal deviation

上述结果验证了本文提出的组合导航方法的可行性，在实验条件下，该方法定位精度达到46mm(116m前进距离)，最终计算的位置偏差精度为：偏差量误差／前进里程＝0.044／116.4287＝0.038%。在实践应用中，水平位置偏差精度约为：0.129／300＝0.043%。相信将该导航方法应用于掘锚机施工中，将为机器设备的导航定位工作提供有力保障。另一方面，为了减小惯性误差累积的影响，保证定位精度和位置偏差精度，通常在载体前进100m左右要做一次坐标修正。

3 结论

基于煤矿巷道施工现场掘进导向的迫切需求，本文提出了一种基于惯性导航和航迹推测的导航定位方法。该方法根据惯导姿态数据、里程计位移数据以及载体零位数据，解算机头／机尾相对于计划线在水平和竖直方向上的偏移量，实现了掘锚机的导向测量功能。在实验环境下进行了定位精度和偏差精度测试，同时进行了在现场施工环境下的应用测试。实验结果表明，该方法偏差解算精度为0.038D%(D为前进距离)，具有很好的工程推广和应用价值。在接下来的工作中，需要研究惯导、里程计的标定方法以及振动环境下的稳定性测试，以提高系统精度。