基于位置观测量的光纤陀螺惯导系泊条件自标定方法

饶国像， 周 元， 杨晓莺

(1.超精密航天控制仪器技术实验室，北京100039；2.北京航天控制仪器研究所，北京100039)

0 引言

光纤陀螺惯导系统通过安装在台体上的陀螺敏感外界角运动，控制台体处于空间稳定状态，是一种全天候、抗干扰、完全自主性的高精度导航系统。光纤陀螺(Fiber Optic Gyroscope，FOG)具有结构简单、动态范围宽、瞬时响应灵敏、可承受较大过载、寿命长等优点，正逐渐发展为高精度导航领域主要的惯性器件之一[1-2]。光纤陀螺惯导系统在导航过程中能够隔离外界角运动，相对惯性空间保持稳定，为惯性器件提供了一个良好的工作环境。惯导系统的导航精度主要取决于惯性测量单元(Inertial Measure Unit，IMU)，由于惯性器件的误差会随时间发生变化，因此需定期对相关误差参数重新标定。对IMU的标定是惯导系统的一项关键技术。

惯导系统的传统标定方法是将其拆卸下来，利用高精度转台，通过不同的位置编排对惯性器件相关误差参数进行标定[3]。为解决分立式标定对硬件设备要求高、操作过程繁琐的问题，出现了系统级在线自标定方法，避免了拆装的复杂性，并维持了长期的使用精度。此方法将IMU进行多位置自主转位，利用IMU敏感重力加速度和地球自转角速度，通过解析法可估计惯性器件的误差系数。如杨立溪[4]设计了一种十六位置的误差标定及自主对准的一体化方案，能够分离出包括方位角在内的42项误差。包为民等[5]从惯导系统误差模型入手，分析了不同位置对估计结果的影响，设计了一种十六位置的最优多位置标定方案。另一种方法是基于导航方式的自标定，在每个位置进行导航解算，导航结果中包含有IMU的误差信息，以导航结果为观测量可分离出误差系数。如翁海娜等[6]针对混合式光纤陀螺惯导系统设计了一种 “速度＋位置”匹配的自标定方法，能在线标定30项误差系数。为进一步提高标定精度与速度，出现了惯导系统连续旋转自标定的方法[7]。李魁等[8]针对混合式惯导系统的结构特点和旋转方式进行误差分析，给出了转位路径的设计原则和可观测性分析方法。上述方案均要求在静基座条件下进行，无法适用于系泊环境条件。杨玉孔等[9]提出了一种针对舰船在锚泊条件下激光陀螺捷联惯导全参数的标定方法，需用外部提供的高精度经纬度作为观测量。Jorgensen等[10]提出了针对捷联惯导在三种环境下的基于Kalman滤波的标定方法，需采用GPS提供精确的位置信息作为观测量。袁鹏等[11]提出了一种针对舰载激光陀螺惯导系统系泊状态的基于 “速度＋位置”匹配的自标定方法，该方法对速度误差进行滤波，会产生相位延迟，无法满足精度要求。以上几种适用于动基座条件的标定方法都需要引入外界参考信息。

在此基础上，本文针对舰船在系泊环境下受到海浪等因素干扰，研究了一种基于位置观测量的高精度惯导系统动基座自标定方法，能够在45min内准确估计出光纤陀螺惯导系统的18项误差系数，并针对不同的系泊环境运动学条件分析其对自标定结果精度的影响，得出了此标定方法的动基座适用条件。

1 惯导系统误差分析

1.1 惯性器件误差模型

以石英加速度计输入轴坐标系为参考基准建立台体坐标系p系(OXpYpZp)，如图1所示。OXp轴与X加速度计的敏感轴重合，OZp轴位于OXp轴与Z加速度计的敏感轴构成的平面内，并与OXp轴垂直，OYp轴由右手定则确定。

图1 台体坐标系示意图Fig.1 Schematic diagram of platform coordinate system

加速度计的误差模型为

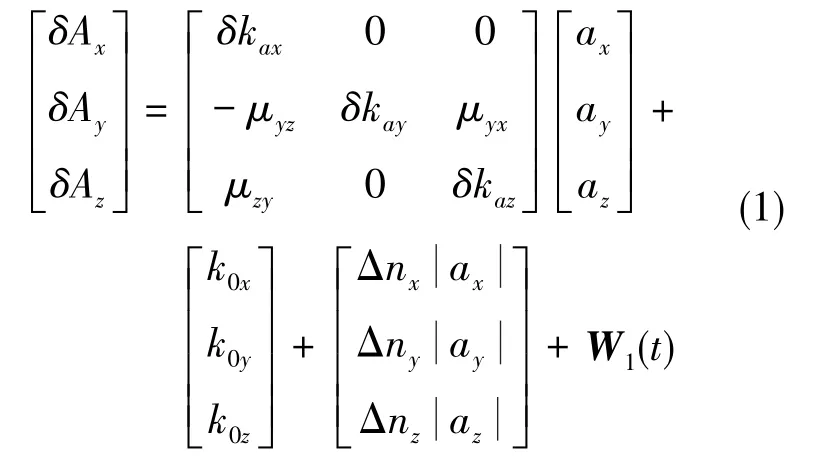
式(1)中，δAx、δAy、δAz分别为x轴、y轴、z轴加速度计的输出误差，k0x、k0y、k0z分别为3个加速度计的零偏，δkax、δkay、δkaz分别为3个加速度计的标度因数误差，μyz、μyx、μzy为加速度计的安装误差，Δnx、Δny、Δnz为加速度计的标度不对称误差，ax、ay、az为台体坐标系下的比力输入，W1(t)为加速度计的随机噪声。

光纤陀螺的误差模型为

式(2)中，δωx、δωy、δωz分别为x轴、y轴、z轴陀螺的输出误差，b0x、b0y、b0z分别为3个陀螺的零次项，δkgx、δkgy、δkgz分别为3个陀螺的标度因数误差，ωx、ωy、ωz为台体坐标系下的角速度输入，gxy、gxz、gyx、gyz、gzx、gzy为陀螺的安装误差，W2(t)为陀螺的随机噪声。

1.2 系统误差方程

选取东天南坐标系为导航坐标系(g系)，设加速度计的输出值为对应台体坐标系下加速度输出为

对应在导航坐标系下的加速度输出为

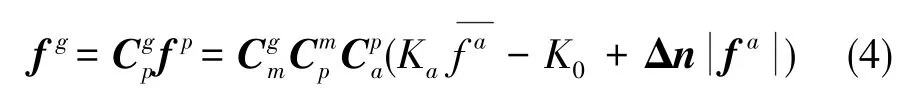
设Xe为包含基座初始对准误差角ϕx、ϕy、ϕz和所有加速度计误差在内的状态向量，有

将式(4)在每个角位置对误差项Xe进行一阶Taylor展开，有

式(7)左边为理想情况下的加速度在导航坐标系下的投影，右边为根据预设的Xe值计算得到的加速度计输出在导航坐标系下的投影。在第一次导航解算过程中，由于对惯导系统各误差系数的预设值不准确，故加速度计算误差在导航系的投影为

由于光纤陀螺惯导的台体能够隔离外界角运动，在导航过程中台体处于空间稳定状态，此时台体相对惯性空间没有角速度输入，陀螺的标度因数误差和安装误差对导航误差影响不显著，故不需要标定，只需考虑光纤陀螺的零偏。导航坐标系下，导航解算的漂移角速度误差主要是由于陀螺漂移和初始方位角不准确引起的地球自转角速度分量误差造成的，则在每个位置上的角速度综合误差为

式(9)中，由方位角误差产生的地球自转角速度在导航坐标系下的投影L为当地纬度。

2 标定方案设计

合理的转位路径可充分激励各项误差系数，利用惯导系统处于导航标定状态时导航解算的位置误差中包含有惯导系统的误差信息，分离出加速度综合误差和角速度综合误差在导航坐标系下的投影，然后根据系统误差方程辨识各误差系数。

在标定加速度计和陀螺误差系数的过程中，采用迭代最小二乘的方法，第一次迭代时默认各误差系数的预设值为零，以后每次迭代结束后，将得到的估计结果对误差系数的预设值修正代入下一次迭代计算中，直至本次迭代结果与上一次迭代结果误差达到预设范围内时迭代结束。

2.1 综合误差辨识

舰载惯导系统处于码头系泊状态时，惯导系统相对地理系的位置变化很小，在标定过程中可认为位置变化近似为零。水平方向上导航解算的位置误差由位置误差初值r0xg和r0zg、速度误差Vxg和Vzg、加速度综合误差Δxg和Δzg、角速度误差ωxg和ωzg引起，用多项式拟合位置误差可表示为

竖直方向的位置误差可表示为

在某一个位置时，第i个采样时刻能得到一个位置观测值rix、riz、riy，有

使用最小二乘的方法可以计算出Δxg、Δyg、Δzg。

当考虑陀螺漂移误差时，水平方向上导航解算的位置误差由位置误差初值、速度误差、水平偏角误差αxg和αzg以及角速度综合误差引起，有

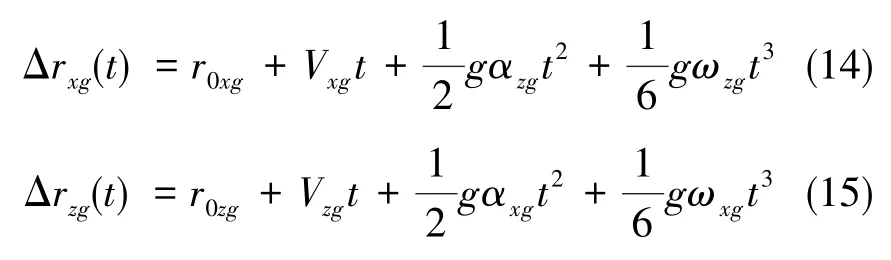
同理，用最小二乘的方法可以计算出ωxg、ωzg。

2.2 基于可观测性分析的转位路径设计

为使光纤陀螺惯导系统各误差系数充分体现在观测量中，需通过不同位置的指向有效激励所有误差源，以提高滤波收敛效果。根据标定要求设计了8位置的转位方案，如表1所示。

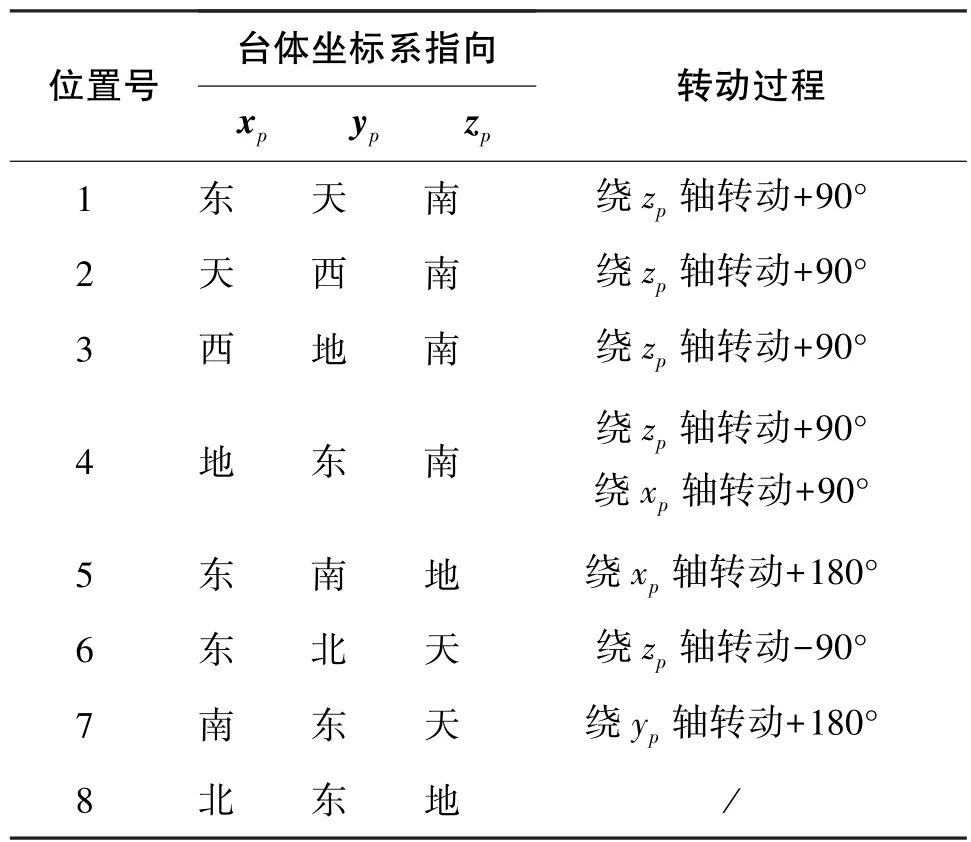
表1 自标定转位位置方案Table 1 Rotation position scheme of self-calibration

根据所设计的位置，可以推导出每个位置下的系统误差方程，由式(8)可得在每个位置的加速度综合误差

由式(9)可得在每个位置的角速度综合误差

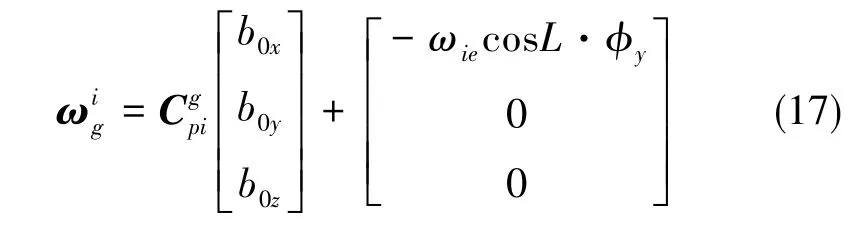
取水平失准角和加速度计误差系数为状态向量Xe1，光纤陀螺的零偏和方位失准角为状态向量Xe2＝[b0xb0yb0zϕy]T，以八个位置加速度综合误差和水平方向角速度综合误差为观测量可得标定过程的观测方程

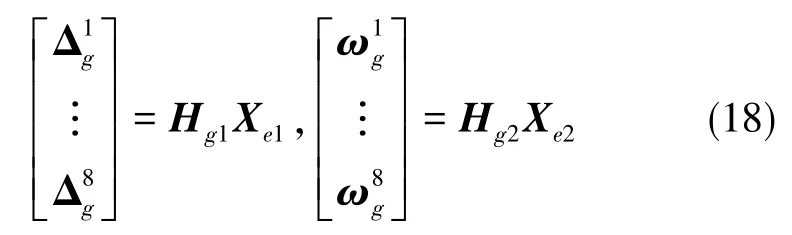
将观测矩阵Hg1、Hg2按位置写成分块形式，具体如下

通过计算可得：rank(Hg1)＝14、rank(Hg2)＝4，观测矩阵都是列满秩，说明系统是完全可观测的，可以估计出所有误差系数。

3 系泊环境运动学模型

通过对舰船在码头系泊环境下采集的运动数据进行分析，可知系泊环境包含纵摇、横摇、偏航3个方向的角运动和3个方向的线运动共6个自由度的运动学模型[12]，其角运动由多个不同幅值和频率的正弦信号叠加而成，在不同海况条件下，其幅值和频率构成有所不同。若通过晃动运动来模拟海浪运动，选取的典型海态环境的运动参数满足：规律性摇摆角运动和线运动的周期为6s～20s，绕方位轴的幅值不超过0.6°，绕水平轴的幅值不超过3.5°，线运动的最大幅值为0.5m。

模拟某典型海态环境的角运动模型

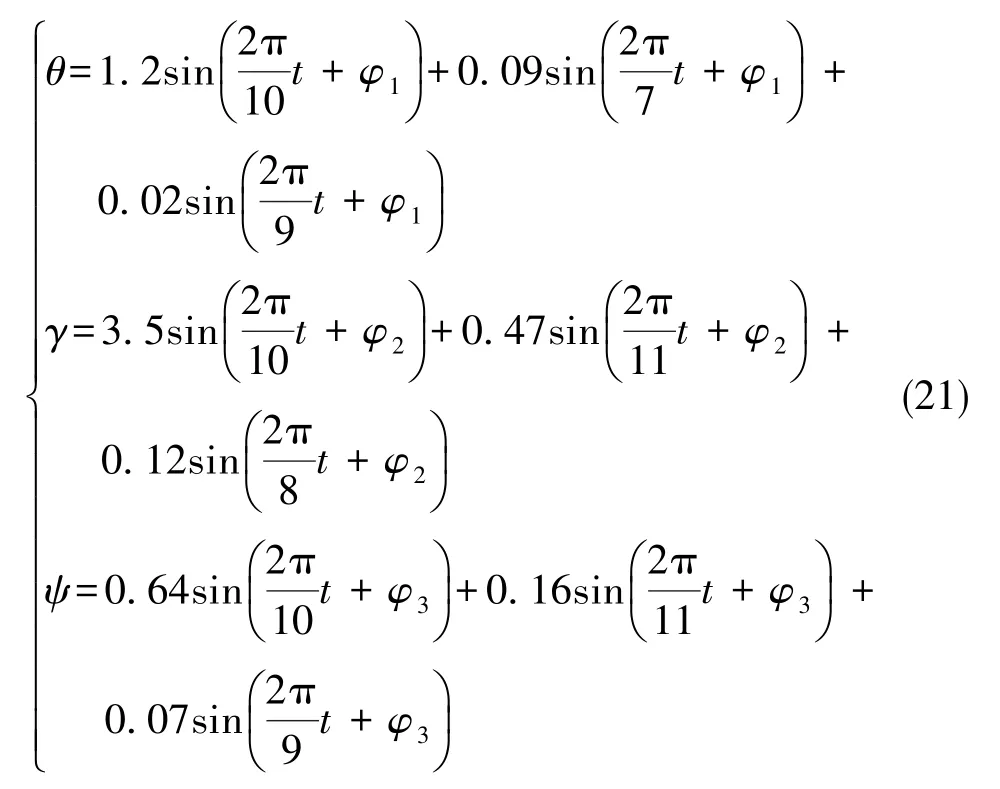
式(21)中，θ、γ、ψ、φ分别为纵摇角、横摇角、偏航角、相位角。角运动的变化曲线如图2～图4所示。

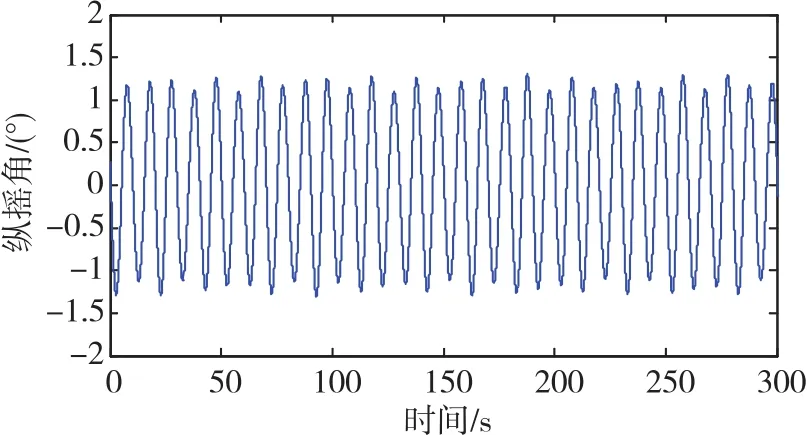
图2 纵摇角变化曲线Fig.2 Curve of pitch angle

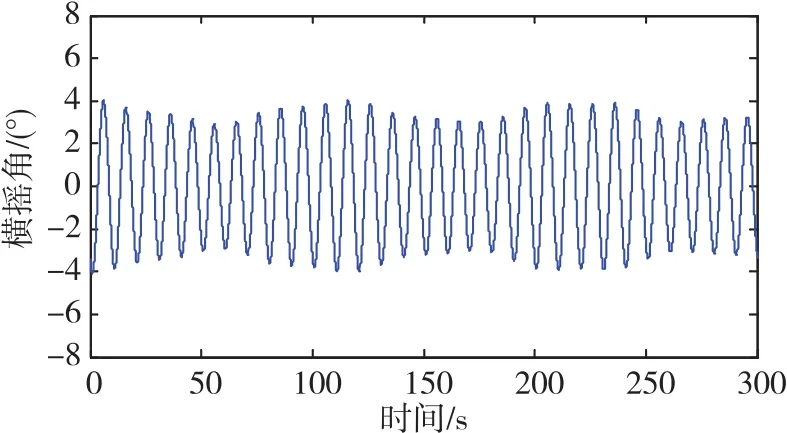
图3 横摇角变化曲线Fig.3 Curve of roll angle

图4 偏航角变化曲线Fig.4 Curve of heading angle

典型的线运动模型如下

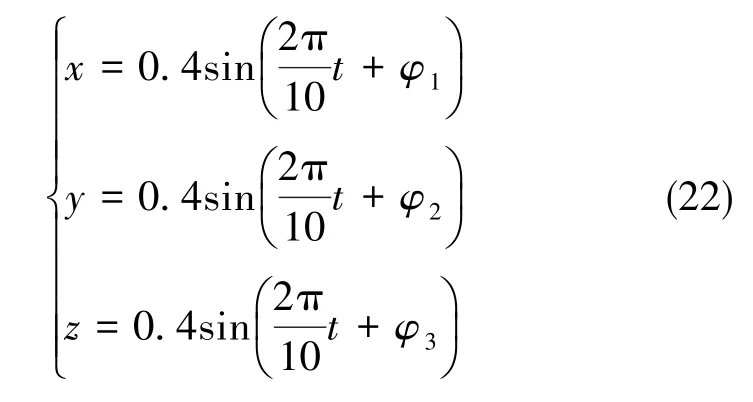
线运动的变化曲线如图5所示。

图5 线运动变化曲线Fig.5 Curve of linear motion

4 仿真结果分析

4.1 典型工况下的标定仿真结果

为了验证此方法在典型工况晃动条件下的标定效果，分别进行了静基座和动基座的仿真实验。利用Monte Carlo仿真方法，在静基座和典型工况晃动条件下根据惯性仪表的统计特性仿真100组数据，假设惯性仪表统计特性满足如下条件：加速度计零偏满足均值≤100μg、标准差为5μg的正态分布，加速度计标度不对称误差满足均值≤1×10－4、标准差为 5×10－6的正态分布， 陀螺零次项满足均值≤0.3(°)／h、标准差为 0.005(°)／h 的正态分布，加速度计和陀螺的标度因数误差满足均值≤5×10－4、标准差为 1×10－5的正态分布， 加速度计和陀螺的安装误差满足均值≤5′、标准差为5″的正态分布。根据3σ原则，可认为惯性仪表的均值统计特性满足以0为均值、最大值的1／3为标准差的正态分布。每个位置的导航标定时间为300s。

按照式(21)、式(22)的系泊环境运动学模型对角运动和线运动求导，可得到系泊环境对惯导基座作用产生的角速度和线加速度，利用Matlab仿真模拟不同环境下惯导系统在标定过程中的输出数据。

采用八位置自标定方法对输出数据进行处理，得到静基座和典型工况下的标定结果误差，如表2所示。表2中，取100次仿真结果中误差系数估计误差的最大值来评估参数标定的精度。由于篇幅有限，给出的典型工况条件下某次标定结果误差变化收敛趋势如图6、图7所示。

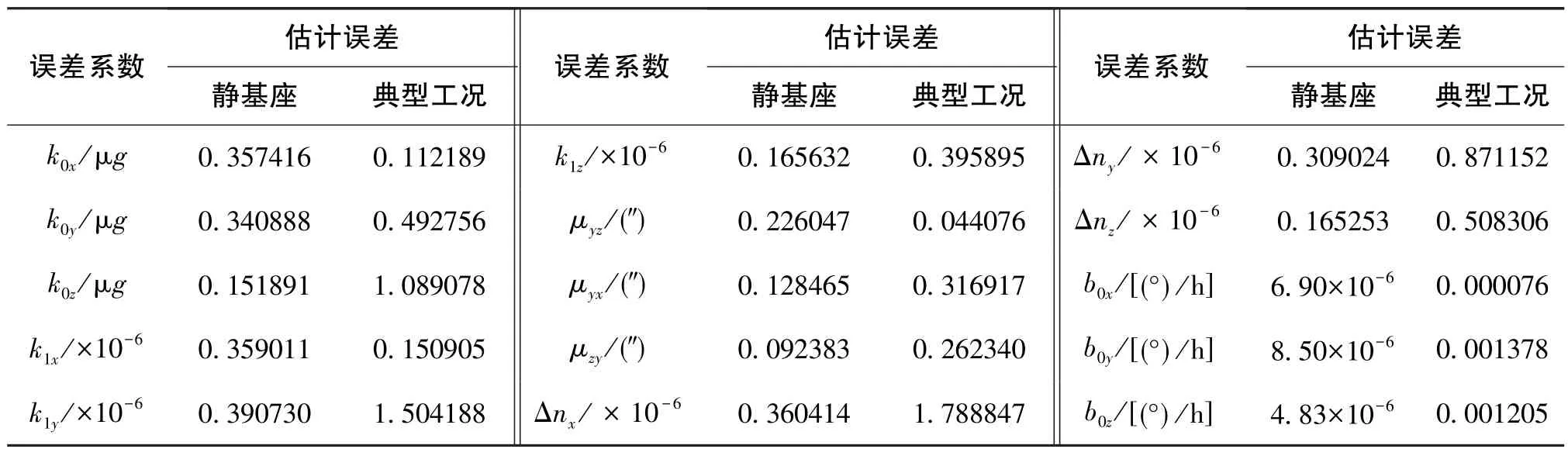
表2 标定误差仿真结果Table 2 Simulation results of calibration errors

图6 加速度计误差估计结果Fig.6 Estimation results of accelerometer errors

图7 陀螺漂移误差估计结果Fig.7 Estimation results of gyroscope bias errors

由表2可知，典型工况环境下，加速度计零偏估计精度优于1.1μg，加速度计标度因数误差估计精度优于1.5×10－6，加速度计标度不对称误差估计精度优于1.8×10－6，陀螺零次项估计精度优于0.0014(°)／h，加速度计和陀螺安装误差估计精度优于 0.4″。

图6、图7为迭代10次后估计误差的变化过程，第10次迭代估计结果与第9次迭代估计结果之差满足迭代收敛条件。由误差系数估计结果变化趋势可知，各项误差系数估计误差收敛于0附近。由多次仿真结果可知，一般迭代4次左右即可满足条件。

4.2 不同晃动条件下的标定仿真结果分析

为分析不同海况条件下光纤陀螺惯导标定的适应能力，针对系泊环境的运动学模型，以典型工况的运动学条件为基准，仿真设置了相位随机获得、不同频率和幅值的多种环境参数作用于惯导系统基座上，具体工况的运动学条件如表3所示。为了更直观地对比估计效果，将不同海况条件下的100组估计误差结果放在同一坐标系中，如图8～图11所示。由于篇幅有限，只给出加速度计零偏和标度因数、陀螺漂移的对比图。每项误差系数求100组估计误差的最大值得到不同海况条件下的标定结果，如表4所示。

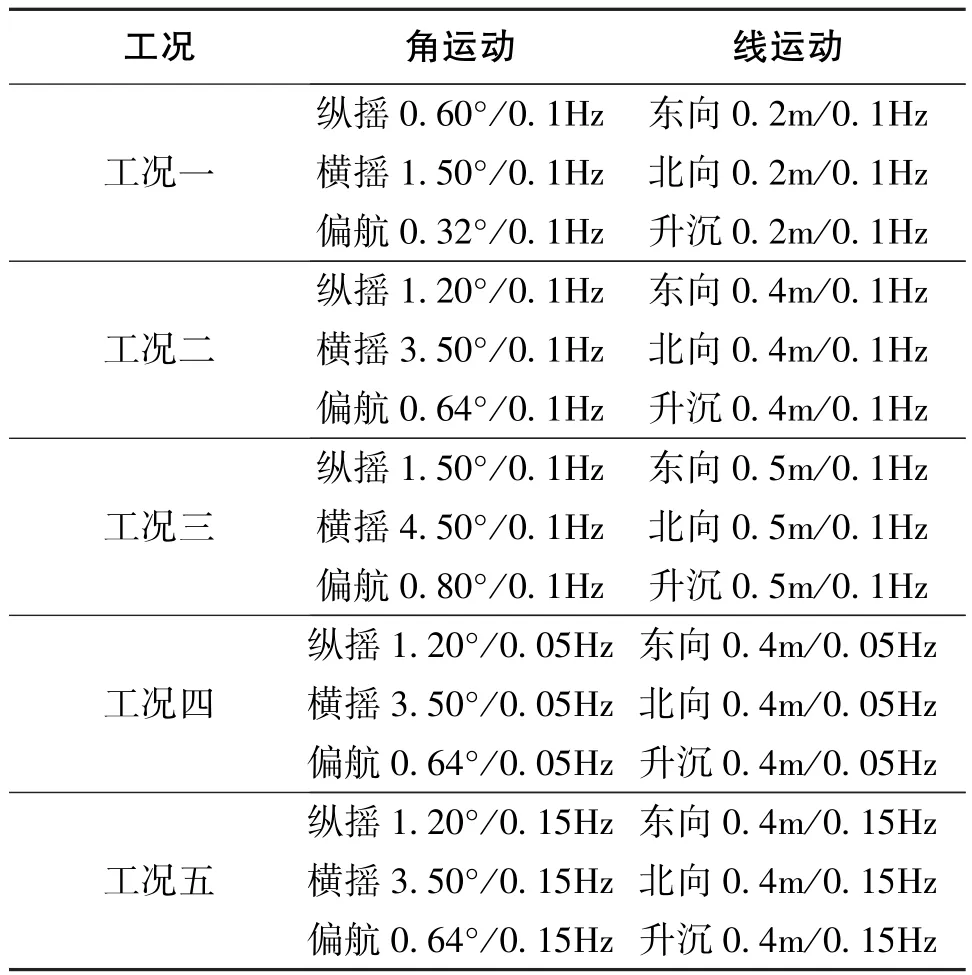
表3 不同海况条件的运动学参数Table 3 Kinematic parameters under different marine conditions

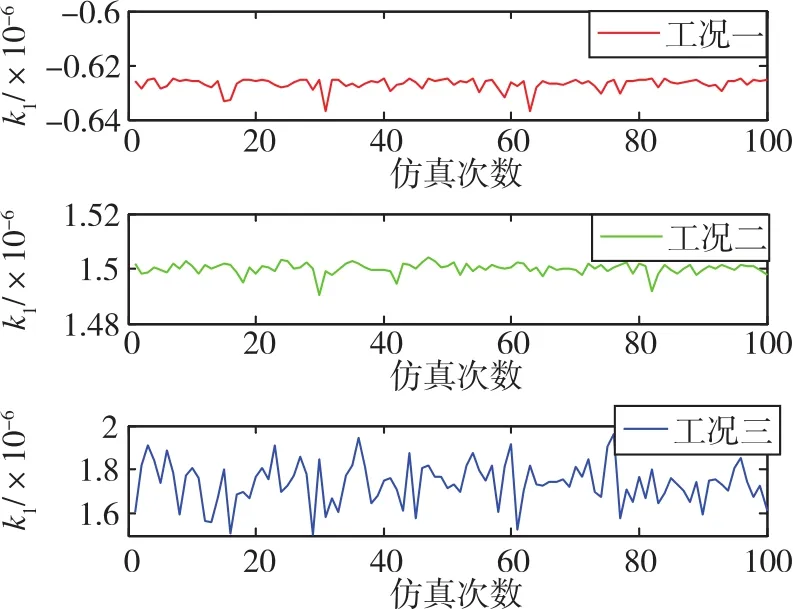
图8 不同幅值条件下加速度计标度因数估计误差对比Fig.8 Comparison of accelerometer scale factor estimation errors under different amplitude conditions

图9 不同幅值条件下陀螺零次项估计误差对比Fig.9 Comparison of gyroscope bias estimation errors under different amplitude conditions

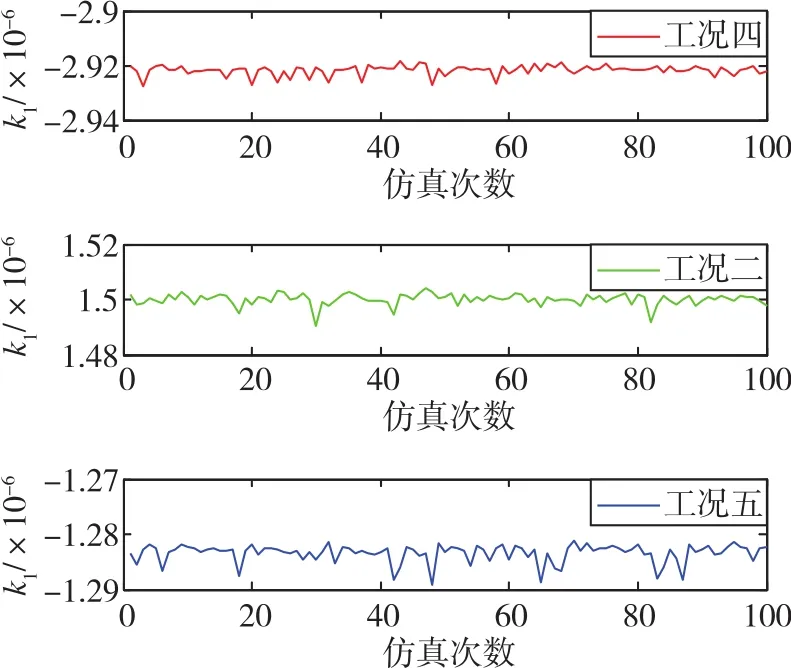
图10 不同频率条件下加速度计标度因数估计误差对比Fig.10 Comparison of accelerometer scale factor estimation errors under different frequency conditions

图11 不同频率条件下陀螺零次项估计误差对比Fig.11 Comparison of gyroscope bias estimation errors under different frequency conditions

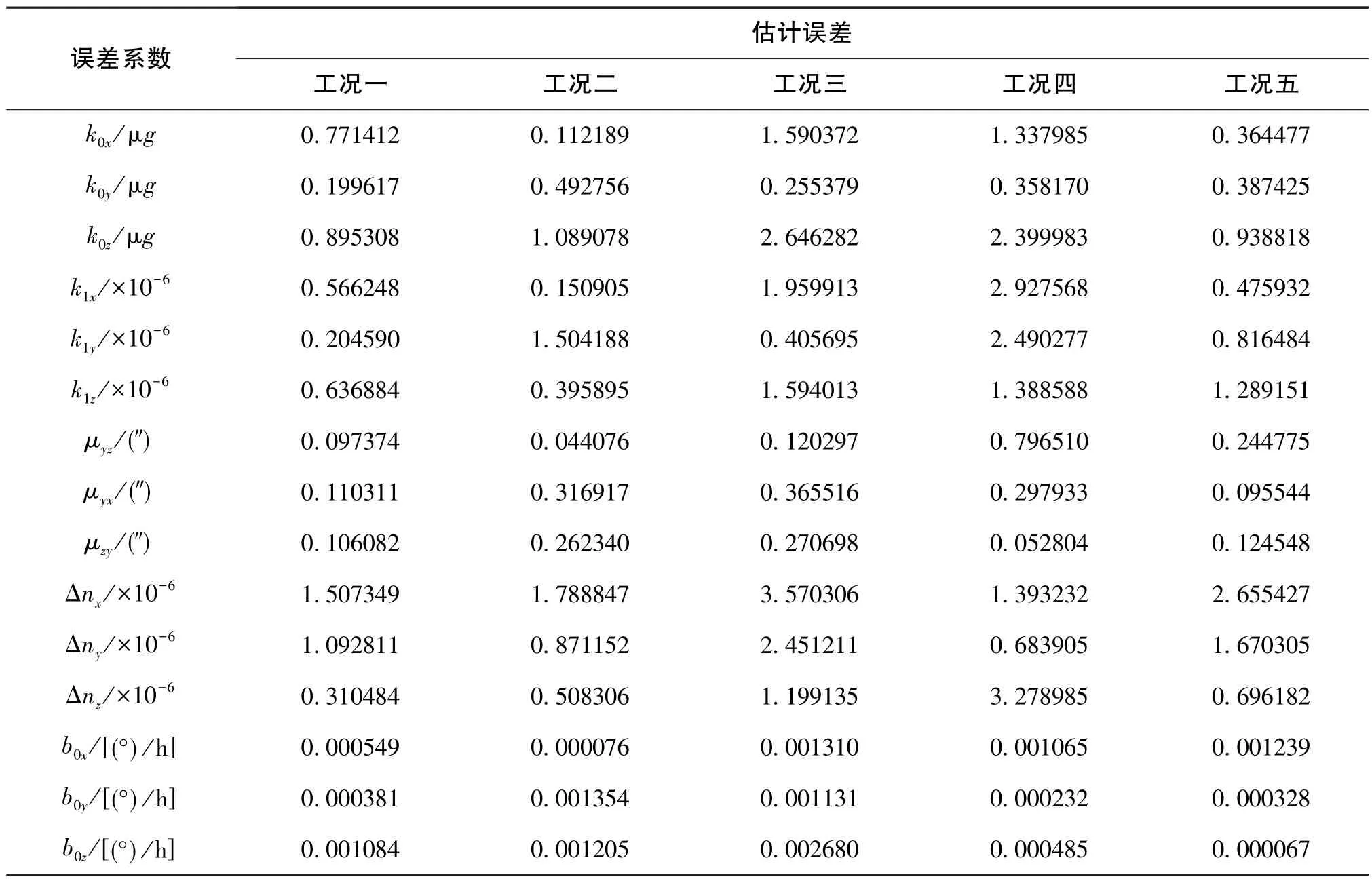
表4 不同系泊工况下的标定误差对比Table 4 Comparison of calibration errors under different mooring conditions

根据表4的估计误差结果，进行以下分析：

(1)海态干扰运动幅值对标定精度的影响

对比工况一、工况二和工况三条件下的估计结果可知，随着干扰运动幅值逐渐增大，加速度计零偏、标度因数、安装误差和标度不对称误差估计误差的最大值逐渐变大，表明加速度计的标定精度逐渐降低；由工况二到工况三的干扰运动幅值变化梯度比工况一到工况二的要小，但是加速度计误差系数估计精度变化更显著，说明在工况三系泊条件附近此标定方法对干扰运动幅值变化更为敏感。从陀螺零次项估计误差结果也可以看出，估计精度随干扰运动幅值变大而降低。

干扰运动的幅值直接影响标定结果的精度，同频率下幅值越大，作用在惯导上的角速度和线加速度越大，对惯性仪表输出的影响越大，导致导航标定过程中位置误差变大，将直接影响标定方法误差。

(2)干扰运动频率对标定精度的影响

对比工况四、工况二和工况五条件下加速度计零偏、标度因数、安装误差和标度不对称误差的估计结果，可知在工况四条件频率最低时(0.05Hz)估计精度最差。陀螺零次项估计误差最大值随着频率的逐渐提高变化不显著，表明在系泊环境频率范围内频率对陀螺零次项估计精度的影响不显著。

本文采用以位置误差为观测量的系统辨识方法估计误差系数，在利用最小二乘估计某位置综合误差的过程中对惯性仪表输出有一个平滑的过程，海态干扰环境的周期性正弦扰动作用会相互抵消一部分。在系泊环境频率范围内，频率越小抵消效果越弱，对标定方法误差影响越大；但是当干扰运动频率过大时(比如频率等于1.5Hz)，会造成作用在惯导上的角速度和线加速度极值过大，使估计结果发散。

5 结论

针对光纤陀螺惯导系统在晃动基座条件下的自标定问题，本文研究了一种基于最小二乘的滤波方法，以导航解算的位置误差为观测量，估计出惯导系统的18项误差系数。该方法不需要引入外界信息，易于工程实现。同时，最小二乘方法对外界扰动作用有平滑效果，可以避免现有Kalman滤波方法由于环境扰动而造成的滤波发散问题。根据仿真结果分析，可以得出如下结论：

1)此方法能够快速、准确估计出相关误差系数，典型工况干扰运动条件下，加速度计零偏估计精度优于1.1μg，加速度计标度因数误差估计精度优于1.5×10－6，加速度计标度不对称误差估计精度优于 1.8×10－6，陀螺零次项估计精度优于0.0014(°)／h，加速度计和陀螺安装误差估计精度优于 0.4″。

2)利用Monte Carlo仿真方法分析了不同海况条件运动的幅值和频率对标定精度的影响，总结出了此动基座标定方法适用的海态干扰环境，对不同海态环境下的惯导自标定工程应用具有参考价值。