情感、价值目标在初中数学教学中的设计浅析
2021-11-03胡媛蔡诗靓唐羽霞
胡媛 蔡诗靓 唐羽霞
摘要:“二期课改”强调教学模式与方法要为完善学生学习方式、促进学生创新精神、提高实践能力服务。现在教师的职责不再是简单的传递知识,而是引导学生自主探索与合作交流,为学生营造积极、和谐、快乐的学习氛围,向学生提供充分参与数学活动的机会。
关键词:情感;价值目标;初中数学
二期课改把课程目标定位在“知识与技能、过程与方法、情感态度与价值观”三个维度。教师在尊重学生人格、关注学生个体差异的同时如何处理好三维目标之间的关系,体现三维目标的多元化,并深刻挖掘隐含在教学内容中的情感、态度、价值观,在初中数学教学中我尝试着做到以下几点:
一、创设问题情景 提高学习兴趣
课堂教学是教师组织和引导学生进行有效学习的阵地,如果在课堂教学中只是简单照本宣科地讲解例题,很难实现预期的教学目标。我根据学生的年龄特征和心理特点,有针对性地选取素材,启迪学生的思维,同时在教学设计中突出一个“新”字,让学生有跃跃欲试的动力。为使学生理解并掌握一次函数计算及应用,我选取如下习题:星期天小鸣和妈妈乘坐出租车去公园,看到车上的标价为:3公里以内10元,超过3公里每公里收1.2元,出租车行驶6公里时,小鸣看到计价器上显示的价格,他们到达目的地后,司机叔叔收了20.8元。请问:(1)小鸣看到的价格是多少元?(2)出租车行驶了多少公里?由于问题环境学生比较熟悉,因此大家积极思考,不仅很快得出答案(1)13.6元(2)12公里。而且理解了k、 b虽然都是常量,但表示的实际意义不同。这样的效果,比单纯解这道题:若已知一次函数解析式y=1.2(X-3)+10.求(1)当x=6时,求y=? (2)当y=20.8时,求X=?教学效果要好。因此,精心设计教学情景,激发学生的求知欲,使学生掌握学习的主动权,产生积极、快乐的情绪体验,从而增强学习自信心,产生自我激励,享受到课堂学习带来的乐趣。
二、实施分层教学 引导自主学习
由于学生的知识积累、情感体验、思维模式等存在差异。因此教师要深入研究学生的学习基础和认知水平,做到因材施教,设计出符合学生实际的学习过程。教学过程还需重点把握一个“活”字。为了使学生理解掌握利用已知条件列出一元二次方程,我将一道习题改编为:公园准备在一块空地上临时搭建大小相等的三个长方形活动场地,总面积为800平方米,可以利用一面墙,现有120米长的隔离带,你能帮他们设计方案吗?学生通过寻找已知条件与未知之间的联系,得出此题的解题思路:1、设矩形与墙垂直的一边长为X米,另一边为(120-4X )米2 、利用矩形面积公式列得方程: X(120-4X)=800 。在此题的基础上,为激发学生的好奇心,培养学生综合解题能力,我对题目适当地进行延伸、变形。再设计以下几个问题让学生去讨论、思考:1)、若上题其他条件不变,但限定墙的长度为N米,则题目的解是否有变化?2)、若上题其他条件不变,但开一扇1米宽的门,则如何列出方程? 3)、若上题其他条件不变,改为两边靠墙围成矩形场地,则又如何列出方程?
本题根据分层教学原理,设计一组具有启发性的变式训练,由浅入深、层层递进,给学生充分的思考空间,使不同程度的学生在学习过程中,都有所收获,在启迪思维的同时真正成为课堂的主人。
三、改进教学方式 培养创新能力
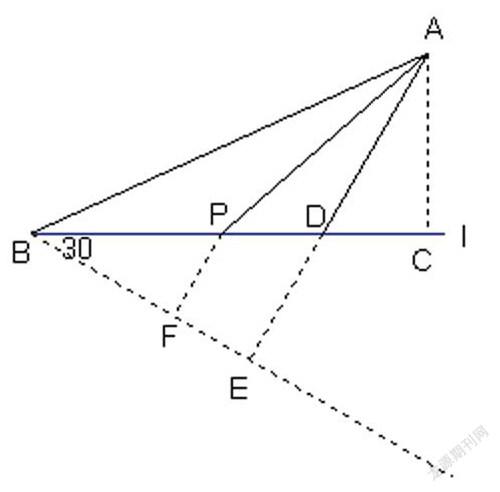
“二期课改”强调教学模式与方法要为完善学生学习方式、促进学生创新精神、提高实践能力服务。现在教师的职责不再是简单的传递知识,而是引导学生自主探索与合作交流,为学生营造积极、和谐、快乐的学习氛围,向学生提供充分参与数学活动的机会。美国数学家波利亚认为:数学教学方法的核心是学生的猜想活动,教师通过指导,借助“再创造”形式,让学生亲身体验、合作交流、创新理念、拓展思维。从而体现探究性学习的“特”字。所以我选择这样一道题目引导学生探究:一条笔直的公路L穿过草原,公路邊有一卫生站A,距离公路30千米的地方有一居民点B,A、B的直线距离是90千米。有一天,某司机驾车从卫生站送一批急救药品到居民点B,汽车在公路上最快速度是60千米/时,而在草地上最快速度是30千米/时。问(1)司机从卫生站A到居民点B的主要途径有几种?(2)司机应以怎样的线路行驶,所用的时间最短?(3)最短的时间是多少?
由于此题内容涉及到行程、解直角三角形的应用、轴对称等问题,有一定难度,所以我设计以下几个问题,进行简单提示:1)、A、B间的最短路线是哪条线段?2)、是否还有其它的路线?AC+BC是否时间最短?3)、设想把公路上行驶路程变成草地上的行驶路程。猜测汽车在何处离开公路行驶时间最短?在解题过程中我鼓励学生大胆质疑、发现问题、探究解决,把课堂还给学生,给学生充足的空间和时间进行探讨,达到师生间思维的碰撞与和谐共振。
情感目标贵在一个“情”, 教师要把自己对学生的感情融入到教学设计中,同时还要鼓励学生独立思考、自主探索、交流共赢。真正体现“以学生发展为本”的教学理念。
