一种基于多频外差的相位解包裹方法
2021-11-03杨延竹苏雪龙
韩 玉,杨延竹,苏雪龙
(1. 东华大学 机械工程学院,上海 201620;2. 上海船舶研究设计院,上海 201203)
相位测量轮廓术是一种基于光栅投影和相位测量的光学三维面形测量技术, 其可有效实现物体表面三维轮廓的自动测量[1]。该方法是将相位作为立体匹配的一个特征量[2],因此高精度的相位解算是准确获得被测物体三维坐标的关键因素之一。相移法是提取相位的常用方法,但是其采用反正切函数求得的相位为包裹相位,由于反正切函数特性所求得的相位包裹在[-π, π],不具有唯一性,所以必须进行相位展开得到连续分布的绝对相位[3]。
目前,相位解包裹方法主要可分为空间相位解包裹和时间相位解包裹两大类[4]。空间相位解包裹的本质是一种积分过程,任何一点的误差都会随展开过程演变成累积误差[5],因此空间相位展开方法一般不适用于高精度及复杂面形的测量[3]。时间相位解包裹算法是将每个像素点的相位值进行独立计算,再进行立体匹配,可以有效避免误差累积,在实际应用中有较高的实用性。多频外差解包裹方法是时间相位解包裹算法中常用的一种方法,但是直接利用多频外差解包裹后的相位会出现跳跃性误差,从而导致三维重建后存在离群点,所以需要进行误差校正[6-9]。雷志辉等[9]对多频外差解包裹进行改进以修正跳跃性误差,但是仅对双频有效,并且在其设定的参考相位的误差大于π时会出现漏判的情况。陈松林等[6]对文献[9]的修正方法进行了改进,但是约束条件较多且实现复杂。
本文针对多频外差解包裹后出现相位跳跃性误差的问题,在深入研究和分析相位误差出现原因的基础上,对现有解包裹方法进行改进,提出一种利用相邻像素点包裹相位获得的斜率和叠栅条纹的整数部分进行双重判断的解包裹修正方法。
1 多频外差解包裹方法
相位测量轮廓术的三维测量原理如图1所示,其中,D为摄像机与投影仪的中心连线距离,L为摄像机光心距参考平面的高度,h为待求被测点的高度。本文采用四步相移法来计算包含有被测物体表面三维信息的相位主值[10]。当向物体表面投影正弦光栅后,采集到的变形光栅图的光强分布如式(1)[11]所示。
Ii(x,y)=a(x,y)+b(x,y)cos[φ(x,y)+θ]
(1)
式中:Ii(x,y)为图像中(x,y)点处的灰度值;a(x,y)为平均灰度;b(x,y)为调制灰度;θ为图像相位移即初相位;φ(x,y)为经物体调制的待求相位值。采用四步相移法通过反正切函数求出相位值[12],如式(2)所示。
(2)
式中:I1、I2、I3、I4分别为4幅相移图像的光强分布。由于反正切函数的性质,由式(2)求出的相位主值φ(x,y)范围在[-π, π]内,但是使用的光栅图像存在多个周期数,除第一个周期内的相位外,后续所求的相位与实际相位相差若干个2π周期,所以必须对求得的相位主值进行相位展开以获得连续的绝对相位值。

图1 测量原理图Fig.1 Measurement schematic diagram
多频外差解相是指将多种不同频率的光栅图像叠加到一起进行解相的方法,最常用的是三频外差解相[4]。
多频外差原理如图2所示,p1、p2分别为两个投影光栅条纹的一个周期长度即节距,λ为频率,周期数为s,λ=1/s,一般p1 (3) 图2 多频外差解原理Fig.2 Principle of multifrequency heterodyne solution 对于物体上同一点,当投影光栅条纹的3种节距分别为p1、p2和p3时,对应的条纹级数分别为n1、n2和n3(包含小数部分),Ni为整数部分,Δni为小数部分,则有式(4)~(7)成立。 ψi=2πni (4) p1n1=p2n2=p3n3=p12n12=p23n23 (5) (6) ni=Ni+Δni,Ni∈Z (7) 式中:φi为相位主值;ψi为解相后的绝对相位值;Z为整数集。由式(4)~(7)可以得到: (8) (9) (10) 从式(8)~(10)可以看出,只需要N1-N2就可以求出n1和n2。根据叠栅条纹的特性可知,假设物体上的某一点位于叠栅条纹的第N12级与N12+1级内,x为其在X轴方向上距离O点的距离,O点相位为0,可以得到: (11) 代入式(10)可得: N1-N2∈(N12+Δn2-Δn1, (12) 又因为 Δn1, Δn2∈(0, 1)⟹Δn2-Δn1∈(-1, 1) (13) 结合式(12)和(13)式可得N1-N2的范围为 N1-N2∈(N12-1,N12+2) (14) 因为N1,N2∈Z,所以N1-N2∈Z,从而得到: N1-N2∈[N12,N12+1](15) 根据N1-N2的范围分析讨论式(12),这里分下列两种情况: (1)当(Δn2-Δn1)时,根据式(13)可得N1-N2>N12,那么由式(15)可知N1-N2=N12+1。 (2)当(Δn2-Δn1)≤0时,根据式(13)可得N1-N2 结合式(6),那么上述两种情况变为 (1)当φ2>φ1时, N1-N2=N12+1 (16) (2)当φ2≤φ1时, N1-N2=N12 (17) 将式(16)和(17)分别代入式(10)并结合式(4),可以求得相位展开后两种条纹的绝对相位ψ1和ψ2。 (1)当φ2>φ1时, (18) (2)当φ2≤φ1时, (19) 由式(18)和(19)可以看出,因为φ1-φ2乘以(p2/p2-p1)/(p1/p2-p1),使得φ1-φ2的误差被放大,又因为ψi又可以表示为ψi=2πNi+φi,采用该式进行求解,可以消除条纹级数小数部分带来的影响,避免误差放大现象的发生,可以通过对ni向下取整获得Ni,所以由式(16)和(17)可得: (1)当φ2>φ1时, (20) (2)当φ2≤φ1时, (21) 同理,结合式(5)可获得以下关系: (22) 将式(22)代入式(8)~(10)可得ψ12和ψ23的如下展开式: (1)当φ23>φ12时, (23) (2)当φ23≤φ12时, (24) 选择合适的p1、p2、p3可以使叠栅条纹的P123覆盖到整个视场中,一般选择p1 为了对基于多频外差的相位解包裹后的相位会出现的误差进行分析,本文在上述试验系统中利用分辨率为1 280像素×720像素的投影仪分别向被测物体投射节距为p1=21、p2=23、p3=25的光栅条纹,所形成的叠栅条纹为p12=241.5、p23=287.5、p123=1510,p123大于1 280,所以其条纹周期可以覆盖整个投影范围,满足测量条件。 本文取解包裹后的连续相位分布图中的第1 030行的790~990列的200个像素,并将这些位置的相位值分布进行绘制,如图3所示。 图3 未修正解包裹相位Fig.3 Uncorrected unwrapped phase 从图3可以看出,解包裹后的连续相位并不是平滑的,在某些位置会出现较大或者较小的跳跃性相位误差。由式(20)和(21)分析可以看出,解包裹算法中对条纹级数进行了向下取整操作,如果取整错误会造成相位的跳跃性误差。通过分析可知,取整的错误主要是因为叠栅条纹的整数部分的判断错误所造成的,取N12还是取(N12+1)是由Δn2-Δn1即Δn12的正负进行判断的,如果当Δn1和Δn2近似相等时,会很容易出现大小判断错误的情况,因为此时无论是Δn1还是Δn2出现小的误差便会引起0到1的跳跃性变化,虽然只是0到1的震荡变化,但是经过[p2/(p2-p1)]放大后,便会造成floor[p2/(p2-p1)]2π倍的误差,如图3中在915像素附近的误差。 除此之外还有其他位置会出现一些较小的跳跃性误差,从式(20)和(21)中可以看出,取整部分除了N12还包括Δn12,也就是Δn1-Δn2,其中Δn1和Δn2自身也会存在误差。由式(6)可知,这部分与相位主值φi的精度有关,通过计算验证发现在绝大部分的位置不会因为此部分误差产生跳变,但是在条纹级数改变处可能会由于取整操作使得条纹整数部分出现幅值为1的跳变,此时便会造成所求条纹的连续相位出现2π的跳跃性误差。 从以上分析可以看出,利用基于多频外差的相位解包裹方法得到的相位存在不同程度的跳跃性误差,从而影响三维重建的效果,因此需要对获得的相位进行修正。利用式(18)和(19)求得的相位误差被放大,但是并不会达到2π倍的误差,所以利用这一特点,雷志辉等[9]利用式(18)和(19)得到的相位作为参考相位ψ1,将利用式(20)和(21)求得的相位ψ2与其进行对比,两者之差绝对值在π以内则认为没有出现取整误差,否则便是出现了跳变。这种修正方法有一定的局限性,如果参考相位出现大于π的误差时,此时|ψ1-ψ2|<π,但是此时也出现2π的跳跃误差,所以将得到错误的ψ2。除此之外,此修正方法也无法消除大的跳跃性误差,效果并不理想。 为了解决上述问题,彻底消除相位解包裹中的跳跃性误差,对外差原理及外差条纹深入研究,发现两种频率的外差条纹图的斜率是不同的,可用利用此特性对包裹相位进行大小比较。此外,两种外差条纹在得到的叠栅条纹中整数部分是相同的,此特性便可以作为包裹相位判断的检验步骤。基于以上发现,本文提出一种新的相位解包裹修正方法,此方法不仅容易实现,而且可以很好地抑制跳跃性误差。该方法实现流程如下: (1)向被测物体透射光栅后,利用相移法求解出p1、p2条纹的包裹相位φ1、φ2。 (2)假设a点为待处理像素点,其中αφ1、αφ2为a点在两幅条纹中的包裹相位,选取在正方向上a点的下一点b点,其中βφ1、βφ2为b点在两幅条纹中的包裹相位。 (3)由图2可以看出,条纹节距小的斜率大,假设p1 (4)按照叠加条纹p12的增大方向,比较αN12和βN12,因为N12为p12条纹级数的整数部分,所以αN12=βN12,若出现αN12≠βN12,则认为a点处两包裹相位大小比较是错误的,取-(Δn2-Δn1)进行解包裹运算。 本文修正方法实现流程图如图4所示。 图4 修正方法流程图Fig.4 Flow chart of correction method 本文算法修正的解包裹相位结果如图5所示。从图5可以看出,在利用本文提出的相位解包裹的多重判定的修正措施后,大大抑制了跳跃性误差的发生,两种跳跃性误差均被消除,包裹相位被展开为连续平滑的绝对相位,且方法实现简单。 图5 本文算法解包裹相位Fig.5 The unwrapping phase of the algorithm in this paper 为了验证本文算法的有效性以及可靠性,选择高精度研磨块作为待测对象,测量其表面平面度(0.1 mm),被测物体高度由游标卡尺测量得到。本试验硬件选用DLP3010型光机模组(1 280×780)和海康MV-CA050-20UM型工业相机(2 592×2 048),算法在vs2017平台下编程实现,采用Intel i7-9700型处理器。 首先利用张正友标定法对系统进行标定获得内外参数,然后采用本文提出的基于多频外差解包裹修正方法对被测物体进行三维测量,本文进行多组试验来验证本文方法的有效性,取其中若干组如图6所示,其中,图6(a)和(b)为两组出现跳变误差的解包裹相位,图6(c)和(d)为使用本文修正方法后的解包裹相位。由图6可以看出,采用本文的解包裹修正方法可完全去除相位跳变误差。修正前后的三维重建效果图如图7所示。 (c) (a) 修正前 (b) 修正后 本文针对基于多频外差的相位解包裹方法进行相位展开后会出现跳跃性误差,通过多频外差解包裹的推导过程和相位分布图像分析误差的种类和来源,发现跳跃性误差主要来源于对整数部分Ni进行取整操作时φ1、φ2的大小比较和自身误差两部分。基于此分析,提出了利用不同频率的相位主值图的斜率不同以及叠栅条纹整数部分相同来对φ1、φ2的大小进行双重判断,试验分析表明,利用此修正方法可以有效去除跳跃性相位误差,得到平滑的展开相位分布图,从而验证了该方法的可靠性。
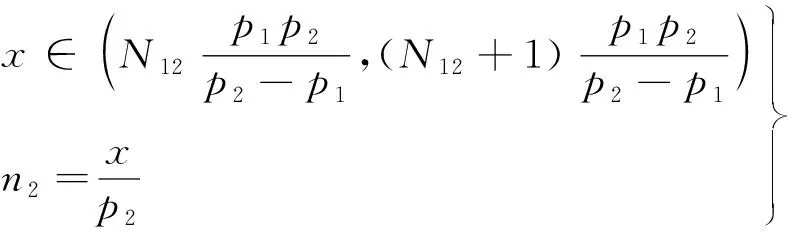
N12+1+Δn2-Δn1)2 相位误差分析及纠正



3 试验分析


4 结 语
