基于Bezier函数方法的球壳振动特性分析
2021-11-03池旭帆束永平
池旭帆,束永平
(东华大学 机械工程学院,上海 201620)
弹性开口球壳结构具有良好的物理特性,因此被广泛应用于航天返回舱、潜水器、管道封头、高压容器等装置。在实际工作环境中,由弹性球壳构成的机械结构需要面临复杂多变的外界环境对结构的振动冲击和负载,当激励频率接近球壳结构固有频率时,可能会导致结构发生共振甚至被破坏,因此研究弹性开口球壳结构的振动特性对保障相关结构的安全具有重要意义。
针对板壳类结构的振动特性,国内外学者分别采用Ritz法[1-3]、有限元法、区域能量分解法[4-6]、动力刚度法[7]等方法相继开展研究。Gautham等[8]采用半解析壳单元对层合球壳结构的轴对称和非轴对称自由振动特性进行了研究。Jin等[9]针对圆柱、圆锥、球壳类结构建立了基于一阶剪切变形理论的改进傅里叶解,采用Rayleigh-Ritz方法对经典约束和弹性约束下结构的频率和模态振型进行求解。Ye等[10-11]采用切比雪夫多项式作为位移容许函数,对任意边界条件下层合开口圆柱壳、锥壳和球壳结构的自由振动特性进行了研究。Qu等[12]采用区域能量分解法对回转锥壳、柱壳和球壳结构在任意边界条件下的振动特性进行了研究。高晟耀等[13]利用改进傅里叶级数表示位移函数以消除边界的不连续性,并利用弹簧参数法来模拟一般边界条件,采用Ritz法求解分析一般边界条件下中等厚度功能梯度球环结构的自由振动特性,探讨了相关参数的影响。李善倾等[14]采用准Green函数方法,将夹支任意形状底扁球壳自由振动问题化为第二类Fredholm积分方程,通过离散化方程对扁球壳的固有频率进行了求解。
现有文献针对壳体结构振动特性展开研究时,多采用引入辅助函数的方法来避免壳体端点位置的不连续问题,同时布置边界弹簧,通过对不同弹簧的适当赋值来实现一般边界条件的模拟[15],这种方式虽然保证了位移函数能够满足连续性要求,但是计算量较大,且在计算前必须先开展弹簧刚度值与一般边界条件的对应关系研究。为避免端点处的不连续问题,同时能够有效模拟一般边界条件,本文采用分段Bezier函数构建的位移函数进行开口球壳结构受迫振动特性分析,旨在为一般边界条件下开口球壳结构的振动问题提供一种新型有效的思路,进一步丰富球壳受迫振动的半解析求解方法。
1 理论方法
1.1 开口球壳结构几何模型
开口球壳的几何模型及坐标系如图1所示。以球壳中面为参考面建立坐标系,其中φ、θ、z分别表示母线方向、周向和法向坐标。设球壳中面曲率半径为R,开口角度为φ0,在z轴方向的厚度为h。

图1 开口球壳结构几何模型Fig.1 Geometric model of open spherical shell structure
1.2 运动学关系与应力合力
根据一阶剪切变形理论,开口球壳上任意一点的位移分量可表示为
(1)
式中:u、v和w分别为结构中面上任意点在φ、θ和z方向的位移;Ψφ和Ψθ分别为中面法线绕φ和θ方向的转角;t为时间。基于球壳中面应变-位移关系得到如下关系式:
(2)
式中:εφ、εθ为中面应变;γφθ、γφz、γθz为中面切应变;χφ、χθ、和χφθ为中面曲率变化;R1=Rsinφ。对于各向同性材料,球壳应变能UV可表示为
(3)
式中:E为材料弹性模量,μ为泊松比。球壳的动能TV可表示为
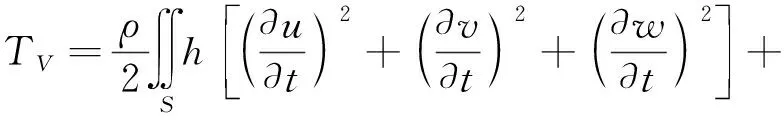
(4)
式中:ρ为材料密度。当球壳结构受简谐力作用时,假设外部载荷全部作用在球壳中面位置处,沿φ、θ、z方向的简谐力分别为Fφ、Fθ和Fz,此时外力做功We可表示为
(5)
1.3 位移函数
在利用能量变分法对结构的振动特性进行求解过程中,结构位移函数的构造对计算结果的精度具有重要意义。为便于适应不同边界条件的情况,选用Bezier曲线来构造位移函数。Bezier基函数的数学表达式如下:
(6)
式中:M为Bezier函数截断阶数,m=0, 1, …,M;x∈[0, 1]。Bezier曲线在端点处的n阶导数仅与相邻的n+1个控制点有关, 满足:
Bi, M(0)=Bi, M(1)=0,i=1, 2, …,M-1
B0, M(0)=BM, M(1)=1
B0, M(1)=BM, M(0)=0
B-1, M-1(x)=BM, M-1(x)=0
B′m, M(x)=M[Bm-1, M-1(x)-Bm, M-1(x)]
利用Bezier函数这种局部性质,在改变边界条件时,只需对个别控制点进行相应的条件约束就可以适应不同的情况,因此边界条件的设置较为方便,并且能有效避免球壳顶点处的不连续问题。相较于引入辅助函数来避免顶点不连续问题的方法而言,选用Bezier函数大大减小了计算量。同时,考虑高阶项需要耗费更多的计算时间,为了在控制点数量不变的情况下,降低函数的最高阶数,从而减少计算量。采用三段Bezier函数表示球壳位移分量沿母线方向的变化,用傅里叶级数表示球壳位移分量沿周向方向的变化。不同方向的位移可表示为
(7)
式中:k为球壳沿φ方向的分解子壳段;n为周向波数,当n=0时,可以得到轴对称模态;akmn、bkmn、ckmn、dkmn、ekmn为5项位移函数的展开系数;j为虚数单位。
如使三段Bezier函数满足应变位移关系式,位移曲线需满足一阶导数连续, 即令
(8)
式中:ι=a,b,c,d,e;k=0, 1。
1.4 振动特性方程的求解
球壳结构的整体能量泛函可表示为

(9)
将式(3)~(5)代入式(9)进行变分运算,并沿一个周期积分,可得到球壳的振动微分方程。当球壳自由振动时,We=0,球壳结构的自由振动微分方程可表示为
(K-ω2M)G=0
(10)
式中:K、M和G分别为刚度矩阵、质量矩阵及未知系数矩阵,G=[akmn,bkmn,ckmn,dkmn,ekmn]T;ω为圆频率。通过求解式(10)即可求得球壳结构的固有频率。
当球壳受简谐激励产生受迫振动时,强迫振动微分方程可表示为
(11)
式中:F为外界简谐激励经变分后得到的载荷向量;K*为阻尼力做功时的刚度矩阵,在考虑复阻尼影响的情况下,K*=(1+jη)K;ωc为激励圆频率。在激励频率给定时,可求得位移展开项的系数向量为
(12)
将位移展开项的系数向量代回各位移函数,即得到在给定激励下球壳上任一点的位移响应幅值。
1.5 边界条件
利用Bezier曲线的局部性,要控制曲线在端点处满足边界条件,只要对少数几个系数进行适当赋值即可。根据Bezier曲线特性可知:
球壳底端固支时,在φ=φ0处,u=v=w=Ψφ=Ψθ=0,可得:
a2Mn=b2Mn=c2Mn=d2Mn=e2Mn=0
球壳底端简支时,在φ=φ0处,u=v=w=Ψθ=Mφ=0,Mφ为φ方向的力矩,可得:
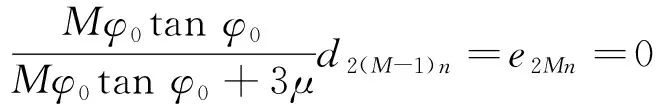
2 自由振动特性分析
2.1 收敛性和有效性验证

2.1.1 收敛性验证


图2 开口球壳轴对称模态的收敛性Fig.2 Convergence of axisymmetric modes of open spherical shell
2.1.2 有效性验证
开口球壳在不同边界条件下的轴对称无量纲频率的计算结果与已有计算结果的对比如表1所示,球壳几何尺寸同上文算例。由表1可知,前5阶轴对称无量纲频率计算结果与文献[16]吻合良好,最大相对误差为7.09%。由此说明本文所用方法适用性强,在不同边界条件下均具有良好的精度。
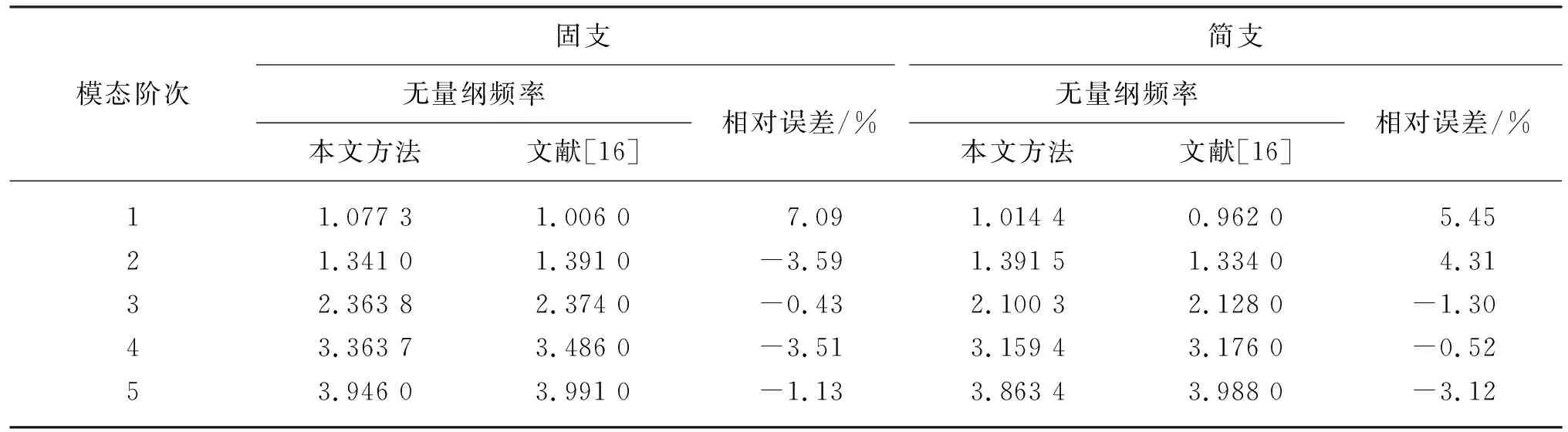
表1 不同边界条件下球壳轴对称无量纲频率对比
开口球壳除了轴对称模态以外还存在非轴对称模态,在承受非轴对称载荷情况下,非轴对称模态也可能被激发出来。底端固支条件下球壳的非轴对称(n≠0)第一阶频率参数对比如表2所示,其中球壳开口角度为φ0=15°,λ为球型扁壳的无量纲几何参数,λ4=12(1-μ2)R2φ04/h2。由表2可知,随着周向波数n的增加,无量纲频率增大,本文计算结果与文献[16]结果的最大相对误差为13.95%,与ABAQUS计算结果的最大相对误差为15.62%。随着球壳几何参数λ与周向波数n的增大,无量纲频率相对误差增大,这可能与周向波数增大后模态振型的复杂变化以及模型简化方式的不同有关。由表1和2可知,本文方法得到的开口球壳轴对称和非轴对称无量纲频率计算结果与参考数据均具有较高一致性,这说明基于Bezier曲线计算开口球壳结构的振动特性是有效的。
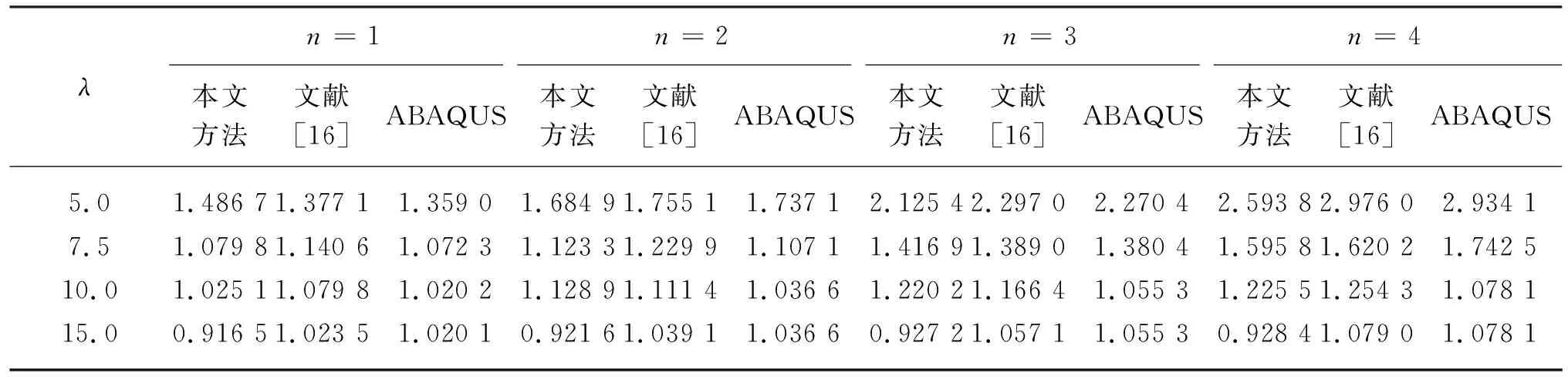
表2 底端固支条件下球壳非轴对称无量纲频率对比
2.2 结构参数对频率影响
固支边界条件下半球壳(φ0=90°)的前4阶轴对称模态对应的无量纲频率与厚度的关系如图3所示,其中,实线为本文方法计算数据,虚线为有限元计算得到的参考数值。由图3可知,固支边界条件下半球壳固有频率随厚度增加而增大,且球壳的高阶固有频率受厚度影响较大。

图3 半球壳前4阶频率随厚度变化曲线图 Fig.3 First four frequencies of hemispheric at different thickness
固支边界条件下开口球壳无量纲频率与开口角度的关系如图4所示,其中,实线为本文方法计算数据,虚线为有限元计算得到的参考数值。由图4可知,开口球壳固有频率随开口角度增大而减小,且固有频率在开口角度较小时变化较大。
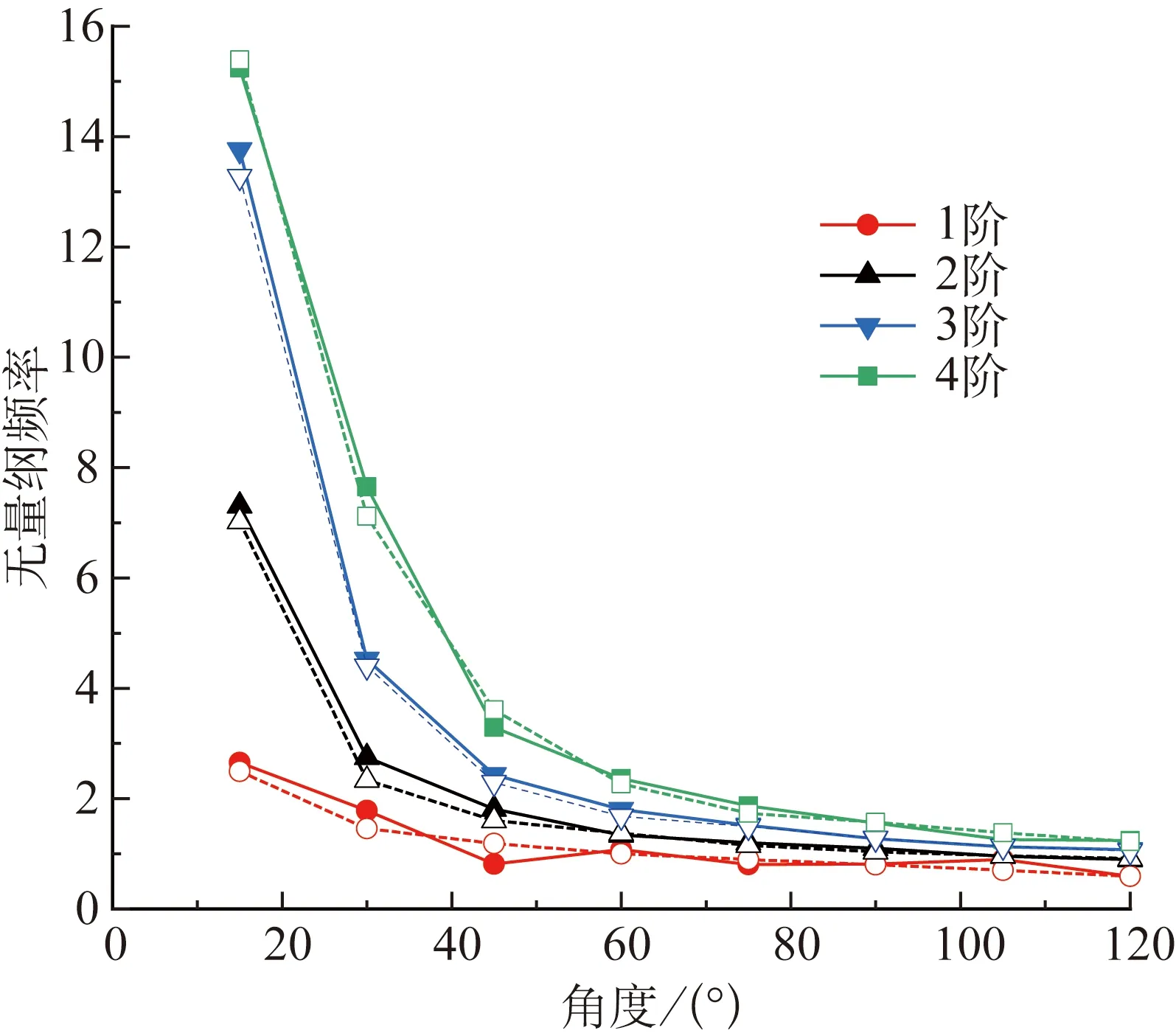
图4 开口球壳前4阶频率随角度变化曲线Fig.4 First four frequencies of open spherical shells at different angles
3 受迫振动响应
球壳的几何参数和材料性质同第2节算例,边界条件为周边固支,研究受简谐力作用下的球壳受迫振动。为研究结构内摩擦对于响应损耗的影响,本文基于复阻尼理论,采用复数弹性模量来表示阻尼力的大小以及阻尼力与应变之间的相位差,E*=(1+jη)E,其中η表示复阻尼,本小节取η=0.001,扫频范围f=10~2 000 Hz,步长Δf=10 Hz,响应点为球壳顶点。选取两种常见简谐激励形式,分别为作用在顶点处的法向点载荷以及作用在中面上的法向面载荷。
3.1 模型验证
在两种载荷作用下,本文方法和有限元方法的球壳结构顶点位置的法向位移响应曲线对比如图5所示。在考虑复阻尼影响时,球壳位移响应曲线在固有频率值附近出现多个大小不一的波峰,这是由复阻尼的特性所导致的,在研究球壳共振特性时,主要考虑峰值较大位置处的共振情况。由图5可以看出,当开口球壳受径向载荷时,两种方法计算得到的振动位移响应值峰值产生一定偏移,在面载荷作用下两者最大偏移相对误差小于5%,在点载荷作用下两者最大偏移相对误差小于2%,因此本文所用方法计算得到的振动位移响应值与有限元方法计算得到的振动位移响应值拟合良好。同时,从图5还可以看出,在低频段位移响应波峰较大,随着激励频率的增大,位移响应峰值逐渐减小,这也是在实际工程中总是关注结构基频的原因。

(a) 面载荷作用下
3.2 结构参数对受迫振动影响
在两种载荷作用下不同开口角度球壳结构顶点的法向位移响应曲线如图6所示。从图6可以看出:在结构参数不变的情况下,球壳受点载荷作用时顶点位置处产生的法向位移响应大于受面载荷作用时;随球壳开口角度的增大,球壳位移响应曲线向着低频方向发生移动;在面载荷作用下,随着开口角度的增大,最大共振峰值增大;而在点载荷作用下,开口角度小的球壳最大共振峰值较大。

(a) 面载荷作用下
在两种载荷作用下不同厚度半球壳结构顶点的法向位移响应曲线如图7所示。从图7可以看出:随着球壳结构厚度的减小,位移响应曲线向着低频方向发生移动,同时响应峰值增大;在低频段(10~1 000 Hz)响应波峰较分散,而在高频段(1 000~2 000 Hz)波峰较为密集。在两种载荷作用下,不同阻尼系数的半球壳结构顶点的法向位移响应曲线如图8所示。由图8可知,当结构阻尼增大时,其共振峰位置几乎不发生改变,而响应峰值明显降低。这是由于随着阻尼力的增大,结构内摩擦所损耗的能量更多,从而造成响应值的下降。

(a) 面载荷作用下
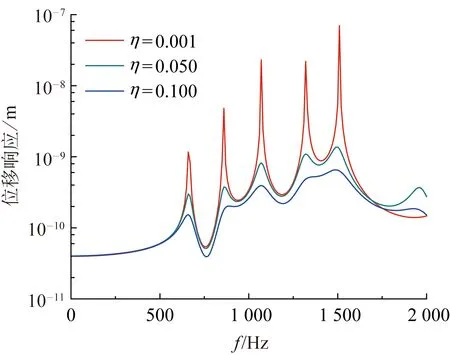
(a) 面载荷作用下
4 结 语
将Bezier函数作为开口球壳结构的位移试解函数建立了开口球壳振动分析模型,采用Ritz法研究了边界条件、结构参数的变化对开口球壳结构振动特性的影响,并通过与已有计算结果进行对比,验证了本文方法的正确性。研究主要得到的结论如下:
(1) 本文方法具有较好的收敛性和较高的计算精度。在收敛性方面,Bezier函数阶数M≥10 时,计算结果收敛,收敛速度快,且具有良好的稳定性。在计算精度方面,本文结果与已有公开发表的文献结果一致性较好。
(2) 球壳结构固有频率不仅与边界条件有关,而且与其自身结构属性有关。开口球壳不同阶次的频率参数均随着厚度的增加而增加,其中高阶频率受到厚度的显著影响。开口角度对球壳振动响应有显著影响,无量纲频率随着开口角度的增大而减小。
(3) 球壳结构受迫振动响应峰值位置受到结构参数和激励形式的影响,其中低频段的响应位置对球壳开口角度、厚度的变化更为敏感。
