碳纤维复合材料汽车传动轴材料结构及性能一体化设计

2021-11-03曹培欢彭梓尧岳晓丽陈慧敏张慧乐

东华大学学报（自然科学版） 2021年5期

曹培欢，彭梓尧，岳晓丽，陈慧敏，张慧乐, b

(东华大学 a. 机械工程学院；b. 上海市轻质结构复合材料重点实验室，上海 201620)

近年来，随着汽车行业的不断发展和人们环保意识的提升，汽车轻量化理念逐渐深入人心，常见的汽车轻量化措施包括汽车结构优化、轻量化材料以及先进制造工艺[1]，其中轻量化材料的使用对于汽车减重效果最为显著。碳纤维复合材料作为一种优异的轻量化材料被广泛应用于汽车轻量化设计[2-4]。

目前，针对碳纤维复合材料传动轴的研究大多对传动轴的结构进行设计。Talib等[5]利用有限元分析法，通过改变纤维缠绕角度研究复合材料传动轴的固有频率。Sriram等[6]设计一款复合材料传动轴，相比钢制传动轴质量大大减轻，同时提高了减振能力。马祥禹等[7]采用理论和仿真的方法对传动轴的扭转特性进行了分析，结果表明所设计的传动轴满足刚度使用要求。种海锋等[8]建立传动轴有限元模型，并对复合材料传动轴的铺层缠绕角度、层数以及厚度进行优化，优化后的传动轴实现了轻量化要求。

综上可知，目前研究人员大多在宏观层面对传动轴的结构以及铺层参数进行设计，以满足传动轴的设计要求，但这种研究方法并不能充分发挥出复合材料“材料可设计性”的特性，即通过设计组分材料的微观结构来进一步提高零件的服役性能。同时，复合材料在制造过程中需满足铺层工艺约束，而现有的研究多数没有考虑铺层工艺要求，这就使得优化结果往往出现不满足工艺约束的情况，难以直接应用于工程问题。

从材料-结构-性能一体化设计角度出发，通过编程实现复合材料传动轴微观结构的参数化建模，采用基于热应力法的均匀化理论预测复合材料单胞的弹性性能，考虑到复合材料的铺层工艺约束问题，对多目标粒子群优化(multi-objective particle swarm optimization，MOPSO)算法进行改进，最后将该一体化设计方法运用于碳纤维复合材料传动轴的优化设计。

1 复合材料多尺度建模及弹性性能预测

1.1 复合材料多尺度建模介绍

研究对象为单向纤维复合材料传动轴，其多尺度结构如图1所示。其中，微观尺度是由纤维单丝和树脂组成，层合板尺度是由多个单层板组成，宏观尺度则以传动轴为研究对象。选择单胞的半边长x1作为微观设计变量，选择每一层的铺层角度x2～x11作为铺层设计变量。在ABAQUS软件中建立微观单胞和传动轴有限元模型，并通过Python编程实现各尺度有限元模型的参数化建模。

图1 复合材料传动轴多尺度示意图Fig.1 Multi-scale schematic diagram of composite drive shaft

1.2 复合材料弹性性能预测

实现微观单胞弹性性能的预测是复合材料传动轴优化设计的基础，采用基于热应力法的均匀化理论[9]，并结合ABAQUS有限元软件求解单胞的弹性性能参数。单胞的等效刚度矩阵Dijmn可以表示为

(1)

ABAQUS软件中位移函数的求解可以通过施加热应力的方式来实现，其中应变与温度差的关系式如式(2)所示。

εmn=-pmn·Δt

(2)

式中：pmn为热膨胀系数；Δt为温度差。

整理式(1)可得：

Dijmn=

(3)

在式(3)中，保持m、n不变，改变i、j的值，可求出单胞的等效刚度矩阵Dijmn。

本文研究的是T700/5015环氧树脂单向纤维复合材料，单向纤维和树脂的材料属性如表1所示[10]。其中，单向纤维等效为横观各向同性材料[11]，树脂等效为各向同性材料。

表1 力学性能参数

在单向纤维复合材料微观单胞类型的选择过程中，首先根据电子显微镜(JSM-IT300LA型)观察T700/5015环氧树脂单向纤维复合材料的微观结构，获取真实微观模型，通过近似处理获得等效模型，再对等效模型进行单胞划分，最终得如图1中所示的正方形单胞[10]，单胞的几何结构参数如图2所示。其中：l为单胞的边长，l=1.5 mm；rf为纤维单丝半径，rf=0.38 mm；h为单胞厚度，h=0.5 mm。

在ABAQUS软件中调用Fortran子程序完成热应力的添加，通过对单胞中对应主从面施加多点约束(multi-point constraints，MPC)实现周期性边界条件的添加，并定义6种不同分析步用来施加不同热应力工况，计算不同热应力工况下等效应力Sij(ij=11、22、33、12、13、23)求解单胞的弹性参数。6种不同热应力工况下的单胞等效应力云图如图3所示。

图2 单胞几何参数示意图Fig.2 Schematic diagram of single-cell geometry parameters

(a) 等效应力S11

(d) 等效应力S12

通过Python编程读取计算结果文件中的应力与应变信息，计算单胞的等效刚度矩阵，并将弹性参数的计算结果与试验值[10]进行对比，如表2所示。从表2可以看出，基于热应力法的均匀化理论获得的弹性性能数值与试验值差异不大，最大误差(3.03%)出现在泊松比处，最小误差(0.59%)出现在剪切模量处。考虑到试验本身存在的误差，可认为采用基于热应力法的均匀化理论能较为准确地预测出单胞的弹性性能。

表2 热应力法所得计算值和试验值对比

2 碳纤维复合材料汽车传动轴性能分析

2.1 传动轴设计要求

研究对象为某公司的lzw6446jy型汽车传动轴的轴管部分，轴管的基本尺寸为长度1 040 mm、内径35 mm、厚度2.5 mm。传动轴所承受的最大扭矩为1 120 N·m，工作最高转速为6 000 r/min，一阶固有频率不小于150 Hz，原钢制传动轴质量为15.509 kg，轴管质量为5.651 kg。

在传动轴设计过程中：作为汽车中主要的传动部件，传动轴主要承受扭转工况，其扭转刚度必须要达到设计要求；而汽车在行驶的过程中，高速运转的传动轴会产生一定的振动，在传动轴对应转速频率下可能会出现共振的情况，这不仅会影响汽车整体的平稳性，也会降低传动轴的使用寿命。因此，在复合材料传动轴的设计过程中，要保证传动轴的扭转刚度和一阶固有频率在满足设计要求的情况下进行轻量化设计。

2.2 扭转刚度分析

衡量传动轴扭转刚度的指标是单位长度扭转角，计算公式如式(4)所示。

(4)

式中：φ为传动轴扭转角，(°)；L为传动轴长度，m；Tm为最大扭矩，N·m；G为剪切模量，MPa；IP为惯性矩，kg·m2。

在ABAQUS软件中建立传动轴的有限元模型，同时在传动轴一端施加扭矩T，另一端采用固支边界条件。图4为传动轴的有限元模型及约束示意图。

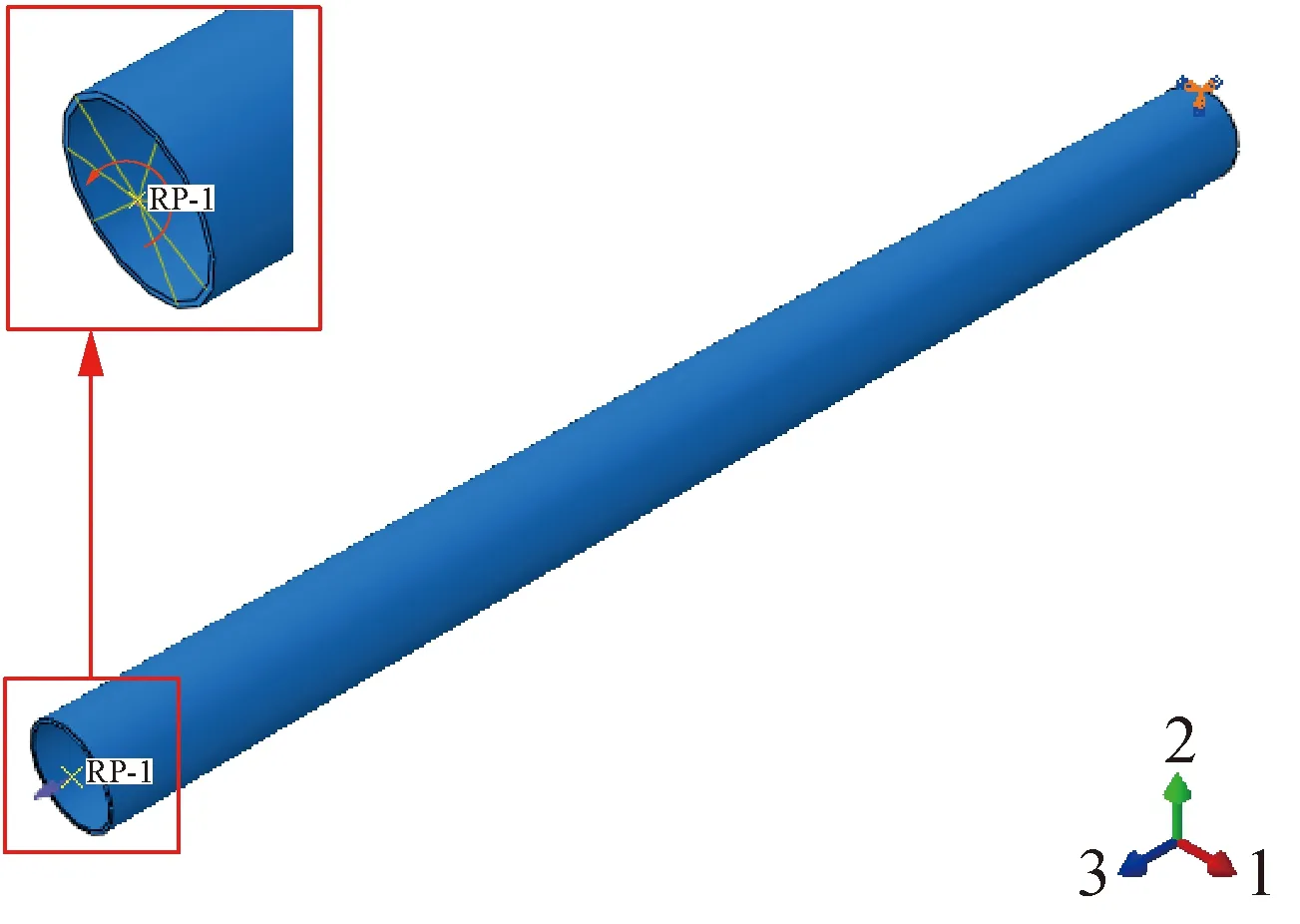
图4 传动轴有限元模型及约束示意图Fig.4 Finite element model and constraint diagram of drive shaft

为探究复合材料中纤维体积分数以及铺层缠绕角度对复合材料传动轴扭转性能的影响，在保证边界条件相同的情况下，分别改变纤维体积分数和铺层缠绕角度进行分析。其中，在探究纤维体积分数对传动轴扭转性能的影响时，建立单层厚度为0.25 mm的10层层合板，层合板铺层角度为[0° 45° 90° -45° 0° 45° 90° 0° 45° 90°]，通过改变设计变量x1的大小, 设计单胞的纤维体积分数分别为35%、40%、45%、50%、55%、60%、65%、70%、75%，进行9组仿真试验。传动轴的扭转刚度与传动轴质量和纤维体积分数的关系如图5所示。由图5可知：复合材料传动轴的单位长度扭转角与其质量是相互冲突的存在；当纤维体积分数增大时，传动轴的单位长度扭转角显著增大，即扭转刚度增大，但同时需要牺牲一定的轻量化目标作为代价。

图5 纤维体积分数对传动轴扭转角和质量的影响Fig.5 Effect of fiber volume fraction on twist angle and mass of drive shaft

在探究铺层缠绕角度对传动轴扭转性能的影响时，选择纤维体积分数为51%的单向纤维复合材料，铺层缠绕角度设计为[0°, 90°]内每隔5°取一组角度，选用10层的层合板进行19组仿真试验。传动轴的扭转刚度与铺层缠绕角度之间的关系如图6所示。由图6可知：随着铺层缠绕角度的增大，传动轴的单位长度扭转角呈“先增后减”的趋势，且当铺层角度为45°时，传动轴的单位长度扭转角最大，即扭转刚度最大。因此，在设计时需要适当提高45°铺层的比例。

图6 铺层缠绕角度对传动轴扭转角的影响Fig.6 Effect of ply winding angle on twist angle of drive shaft

2.3 模态分析

在模态分析理论中，根据有限元法可得传动轴的运动微分方程，如式(5)所示。

(5)

当外界激励为零时，式(5)可以写为

(6)

式(5)对应的特征方程为

(K-ω2M)x=0

(7)

式中：ω为传动轴的固有频率。

基于上述理论，在ABAQUS软件中对复合材料传动轴进行自由模态分析。采用与第2.2节中研究纤维体积分数与传动轴扭转刚度完全相同的分析方案，不同之处在于，在研究纤维体积分数及铺层参数对传动轴模态的影响时，需要先在有限元软件中对传动轴有限元模型的模态分析步骤进行设置，以探究纤维体积分数及铺层参数对复合材料传动轴一阶固有频率的影响。图7为传动轴一阶固有频率与纤维体积分数及铺层缠绕角度的关系。

(a) 纤维体积分数

(b) 铺层缠绕角度

由图7可知：纤维体积分数及铺层缠绕角度对复合材料传动轴的固有频率影响显著。随纤维体积分数的增大，传动轴固有频率随之增大；随铺层缠绕角度的增大，传动轴的固有频率呈下降趋势，当铺层角度超过50°时，传动轴的固有频率趋于稳定，且随铺层缠绕角度的持续增大，固有频率略有增大。

3 碳纤维复合材料汽车传动轴一体化优化设计

3.1 复合材料汽车传动轴优化问题定义

考虑复合材料传动轴的扭转刚度、模态以及轻量化等要求，以传动轴的质量m和单位长度扭转角θ为优化目标，以一阶固有频率f、蔡吴失效准则和铺层工艺为约束，以微观单胞半边长x1和铺层缠绕角度x2～x11为设计变量。各尺度设计变量示意图如图1所示，复合材料汽车传动轴数学优化模型见式(8)。

(8)

式中：X为设计变量向量，Xa、Xb分别为设计变量下、上限；M(X)为传动轴的质量函数；θ(X)为单位长度扭转角函数；f(X)为传动轴一阶固有频率函数。x1取值为5.5～8.0 mm；x2～x11每个变量有-45°、0°、45°和90°共4种铺设角度，分别用0、1、2、3进行编码；Nu为传动轴第u个铺层的缠绕角度。采用的铺层缠绕工艺[12]约束如下：

(1) 铺层定向原则，选择0°、90°和±45°作为铺层角度；

(2) 对称铺设原则；

(3) ±45°单层板对称铺设原则；

3.2 一体化优化设计过程

以传动轴为研究对象，开发一种单向纤维复合材料一体化优化设计方法，优化过程如图8所示。首先，在ABAQUS软件中建立单胞模型，利用Python编程实现微观单胞的参数化建模，并采用基于热应力法的均匀化理论预测单胞的弹性性能。然后，建立复合材料传动轴的有限元模型，利用编程实现微观单胞弹性参数-传动轴材料参数的传递。最后，使用基于改进的MOPSO算法对传动轴的纤维体积分数和铺层缠绕角度进行优化。

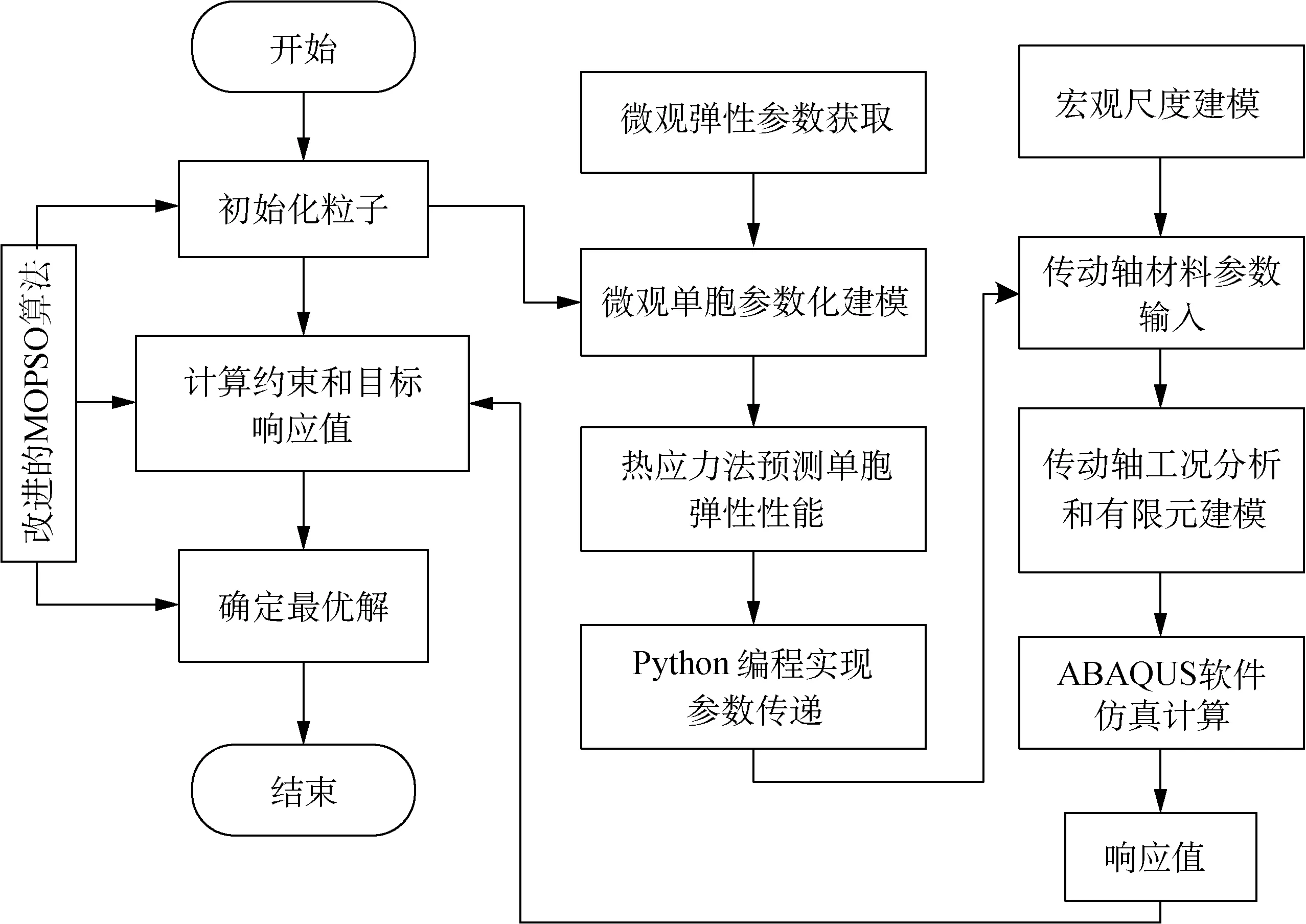
图8 复合材料传动轴一体化优化设计流程Fig.8 Flow chart of integrated optimization design for composite drive shaft

3.3 改进的MOPSO算法

粒子群算法中的每个粒子都对应于设计空间中的解，通过粒子的位置和速度更新找到全局最优解，其中粒子i的速度和位置更新公式为

vik=wvi(k-1)+c1r1(pi-xi(k-1))+
c2r2(gi-xi(k-1))

(9)

xik=xi(k-1)+vi(k-1)

(10)

式中：vik和xik分别为第k步迭代过程中粒子i的速度和位置；c1和c2分别为个体学习因子和全局学习因子；w为惯性常数；pi和gi为粒子i最优位置和全局最优位置；r1和r2为随机数。

传统的粒子群算法多用于解决连续变量的优化问题，本文的传动轴优化案例同时包含离散和连续设计变量，且在优化过程中需要考虑铺层缠绕工艺的约束，需要对算法中粒子的生成和更新策略进行改进。采用基于改进的MOPSO算法流程如图9所示。

图9 基于改进的MOPSO算法流程图Fig.9 Flow chart of improved MOPSO algorithm

3.4 优化结果

采用一体化优化设计方法对传动轴在有、无铺层缠绕工艺约束下进行优化设计，使用MOPSO算法收敛后的Pareto最优解集如图10所示。采用最短距离法[13]从Pareto最优解集中获取一个理想解(图中Knee Point)。

(a) 有铺层缠绕工艺约束

由图10可知：复合材料传动轴在有、无铺层缠绕工艺约束时优化得到的解集具有相似的变化规律。有铺层缠绕工艺约束得到的最优解集扭转刚度虽有一定程度下降，但最优解满足铺层缠绕工艺；无铺层缠绕工艺约束得到的最优解集的轻量化程度虽略有提高，但并不满足实际的工艺约束，不利于复合材料传动轴的批量化生产。

在复合材料传动轴一体化优化设计过程中，考虑铺层缠绕工艺约束时，最优解：纤维体积分数为68.4%，铺层角度为[45°，0°，90°，0°，-45°，45°，0°，90°，0°，-45°]。不考虑铺层缠绕工艺约束时，最优解：纤维体积分数为65.6%，铺层角度为[15°，-6°，-15°，48°，72°，-36°，45°，20°，-8°，-15°]。最优解下的传动轴扭转变形云图和一阶固有频率振型如图11和12所示。

将最优解下的复合材料传动轴性能与金属(钢制)传动轴进行对比，结果如表3所示。由表3可知：相比金属传动轴，单向纤维复合材料传动轴在满足刚度及模态性能指标的前提下，轻量化效果显著，其中，有、无铺层工艺约束最优解下的传动轴质量分别降低22.8%和29.4%。对比有、无铺层工艺约束最优解下的传动轴性能，前者轻量化效果虽不如后者，但固有频率更高，可有效避免共振现象的发生，同时有铺层工艺约束下的最优解可直接用于指导复合材料传动轴的批量化生产。

[3]靳相木等：《基于三维生态足迹模型扩展的土地承载力指数研究——以温州市为例》，《生态学报》2017年第9期。