复合材料周期结构数学均匀化方法的一种新型单胞边界条件

朱晓鹏， 陈 磊, 黄 俊

(1.安徽华电工程咨询设计有限公司，合肥 230022； 2.北京航空航天大学 航空科学与工程学院，北京 100191；3.北京航空航天大学合肥创新研究院，合肥 230012)

1 引 言

复合材料具有比强度高和比刚度大等优点，广泛应用于航天和航空工业领域。众所周知，对于很多复合材料的宏观解，如低阶频率和模态，可以使用等应变模型或等应力模型[1]以及其他均匀化方法[2]，但相对于宏观应力分析，细观分析要复杂很多。为了在计算精度和效率之间达到平衡，各种多尺度方法相继提出，如数学均匀化方法MHM[3,4]、广义有限单元方法GFEM[5,6]、多尺度有限单元方法MsFEM[7,8]、异类多尺度方法HMM[9,10]以及多尺度特征单元方法MEM[11,12]，在这些方法中，数学均匀化方法是具有代表性的方法，文献[13-21]都作了详细的阐述；文献[22-28]讨论了数学均匀化方法的摄动阶次和使用的单元阶次对计算精度的影响，在单胞上施加四边固支边界条件求解其影响函数控制方程，结果显示对于一维结构是精确的，但对于二维结构计算精度不尽人意。

本文在文献[22,24]的基础上详细研究了单胞影响函数控制方程在周期复合材料结构中的真实边界条件，并以此为标准检验数值计算中施加的周期边界条件计算精度，提出更为合理的二维结构单胞周期边界条件。

2 数学均匀化方法矩阵列式

基于微观周期性和单胞域的一致性假设，均匀化理论将异质边界值问题分解为单胞(微观)问题和结构问题(宏观)，二维周期性复合材料结构的控制方程为椭圆型偏微分方程：

(1)

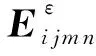
(2)

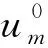
文献[22,24]强调了二阶摄动对数学均匀化方法计算精度的重要性，所以本文同样考虑了二阶摄动项的计算精度。

表1给出了一阶和二阶摄动位移的解耦形式以及影响函数的控制方程，其中EH为均匀化弹性模量，控制方程中的算子yj·和yn分别为散度和梯度。影响函数是单胞尺度(微观尺度)y的函数，而均匀化位移及其各阶导数只依赖于宏观尺度x。从解耦形式和影响函数控制方程可以得到很多信息，详见文献[24]。

表1 摄动位移和影响函数控制方程Tab.1 Perturbed displacements and governing equations of influence functions

数学均匀化方法一般是通过有限元方法得以实现，所以需要将包含二阶摄动项的数学均匀化方法的数学表达式通过加权残量方法转化为易于编程计算的矩阵列式，解耦的单胞影响函数控制方程矩阵列式为

(3)

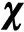
(4，5)

(6)

宏观均匀化位移控制方程为

KHu0=F0

(7)

(8)

式中D⊂Ω表示周期复合材料结构特定单胞区域，g为结构中单胞的数量。

求解结构宏观位移导数和各阶影响函数之后，宏观结构单元节点的真实位移计算公式为

(9)

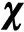
值得注意的是，对于周期复合材料结构，虚拟载荷和虚拟位移是以单胞为基本单位，且具有周期性，所以可以直接通过单胞结构计算其虚拟位移，然后复制到整个结构上，从而得到宏观结构的虚拟载荷和虚拟位移，进而计算真实位移，此举主要是减少计算量以提高计算效率，这也是数学均匀化方法在实际工程中得以广泛应用的关键优势所在。另一方面，为了求解方程(3)得到虚拟位移，需要施加周期性边界条件，所以虚拟位移的计算精度很大程度上取决于周期边界条件选择的合理性，最理想的情况是施加的周期边界条件能够反映单胞在结构中的真实边界变形情况，即可不因边界条件的施加而引入误差。

3 二维周期复合材料结构

为了更加详细地研究周期复合材料单胞边界条件问题，考虑一个四边固支的矩阵平面周期复合材料结构，其结构尺寸为45 mm×45 mm，如图1所示，每个单胞尺寸为9 mm×9 mm，内部包含一个矩阵夹杂，基体和夹杂的弹性模量分别为E1=2.97 GPa和E2=90.585 GPa，泊松比均为0.33。

图1 二维周期复合材料及其单胞结构

3.1 单胞真实位移边界条件

为了施加更为合理的单胞周期边界条件，首先必须弄清求解影响函数控制方程(3)时，单胞在宏观结构中真实的边界情况，有效的方法是将整个宏观结构作为一个大单胞来处理，即可避免额外施加单胞边界条件，直接使用结构边界条件求解虚拟位移(方法1)，这样得到的虚拟位移在结构内部每个单胞边界上的情况即为单胞真实位移边界条件。

一阶虚拟载荷F1由材料弹性参数矩阵决定，与单胞边界条件无关，如方程(6)所示，F1矩阵的 3列 作为3个相互独立的虚拟载荷作用在结构上，其矢量如图2所示，分别对应F1矩阵的第1至第3列。可以看出，与F1相关的 3个 独立虚拟载荷只有在基体和夹杂的交界线上具有非0的分段线性载荷。

图2 宏观结构F1矩阵矢量

(1) 宏观结构内部单胞的真实边界条件具有周期性。

(2) 宏观结构内部单胞边界的虚拟位移是非0的，图3(c)表现尤为明显。

图3 宏观结构真实边界条件一阶虚拟位1变形图

(3) 宏观结构单胞内部虚拟位移和边界虚拟位移相差较大。

图4 宏观结构F2矩阵矢量

(1) 宏观结构内部单胞的真实边界条件仍然具有周期性。

(2) 宏观结构内部单胞边界二阶虚拟位移相对一阶虚拟位移变形更为明显。

3.2 单胞影响函数控制方程边界条件

3.2.1 四边固支边界条件

尽管四边固支边界条件广泛应用于数学均匀化方法处理单胞边界问题，但其对各阶影响函数求解精度的影响尚未得到充分的研究。为了弄清该边界条件的合理性，从结构中取出一个单胞施加四边固支周期边界条件分别计算一阶和二阶影响函数，然后利用单胞结构的周期性复制到整个结构中去，得到结构的虚拟变形图(方法2)，与3.1节(方法1)得到的虚拟位移结构变形图进行对比。

结构的一阶和二阶虚拟位移结构变形图分别如图6和图7所示，分别与3.1节的图3和图5进行对比可以得到，

图6 使用单胞四边固支周期边界条件的一阶虚拟位移1结构变形图

图7 使用单胞四边固支周期边界条件的二阶虚拟位移2结构变形图

(1) 对于一阶虚拟位移，方法1和方法2的虚拟位移结构变形图的差别主要集中在单胞边界上，但并不明显。四边固支边界条件决定了单胞边界上节点虚拟位移为0，而真实单胞边界条件中边界虚拟位移较小，所以使用四边固支边界条件求解一阶虚拟位移是合理的。

(2) 对于二阶虚拟位移，方法1和方法2得到的虚拟位移结构变形图的差别十分明显，同时表现在单胞边界上的节点和单胞内部的节点，所以使用四边固支边界条件求解二阶虚拟位移是不合理的，会造成很大的计算误差。

3.2.2 超单胞周期边界条件

从3.2.1节可以看出，尽管使用四边固支周期边界条件求解单胞虚拟位移较为方便，但对于二阶虚拟位移的求解精度却难以接受。实际上，单胞作为结构基本周期单元包含了所有的微观信息，而且单胞的虚拟位移在边界上取决于其在结构内部周围单胞的相互作用，由此提出超单胞周期边界条件(方法3)，即在9个单胞(3×3)组成的一个超单胞上施加四边固支边界条件，如图8(a)所示，具体实现过程如下。

(1) 使用公式(3)计算超单胞的一阶和二阶虚拟位移。

(2) 将超单胞中9个单胞根据其在超单胞中的位置分为9种单胞，分别为A，B，C，D，E，F，G，H和I，如图8(b)所示，每个单胞均有独立的一阶和二阶虚拟位移。

(3) 将单胞E的一阶和二阶虚拟位移复制到结构内部的每一个单胞上，A，B，C，D，F，G，H和I共8个单胞的一阶和二阶虚拟位移根据其在超单胞中的位置分别对应复制到结构边界上的单胞，如图8(c)所示。

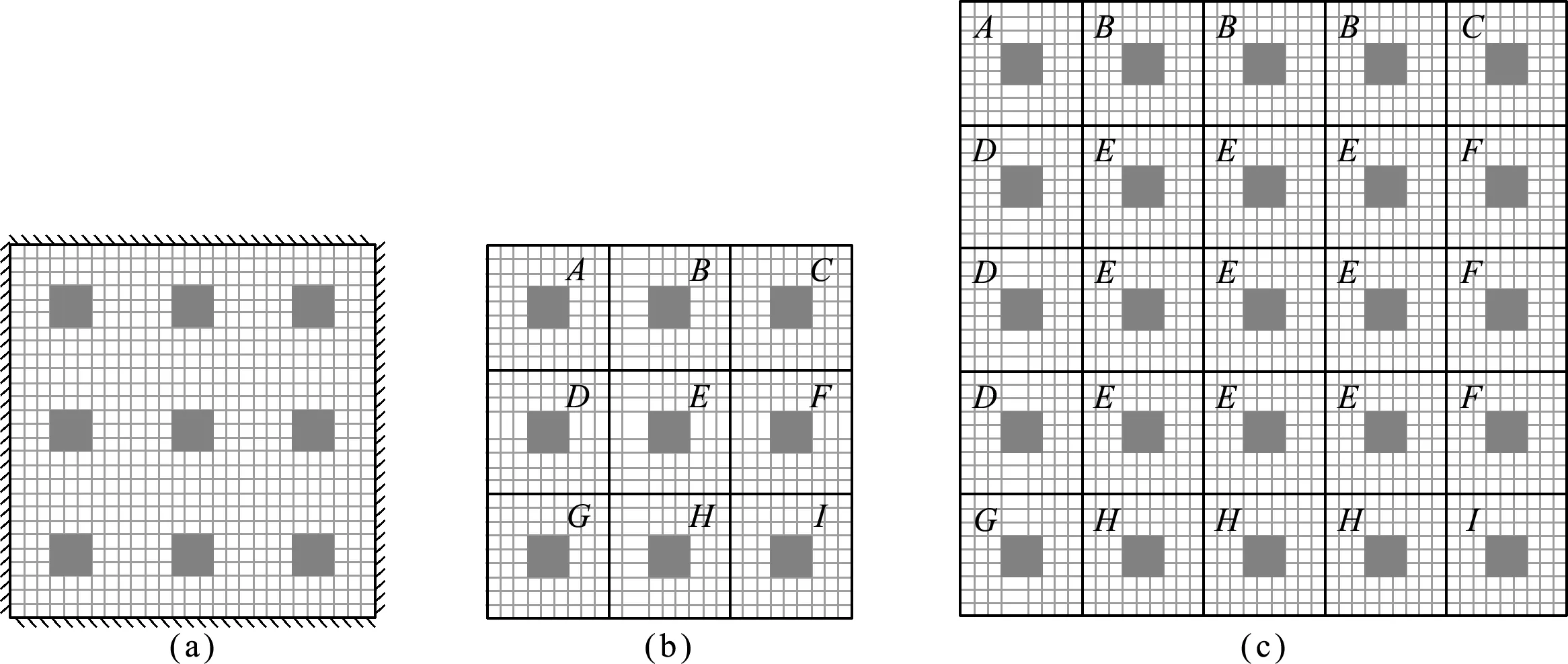
图8 超单胞边界条件实现过程

由超单胞周期边界条件计算得到的一阶和二阶虚拟位移结构变形分别如图9和图10所示，将其分别与图3和图5对比，可以得到，

图9 使用超单胞周期边界条件得到的一阶虚拟位移1结构变形

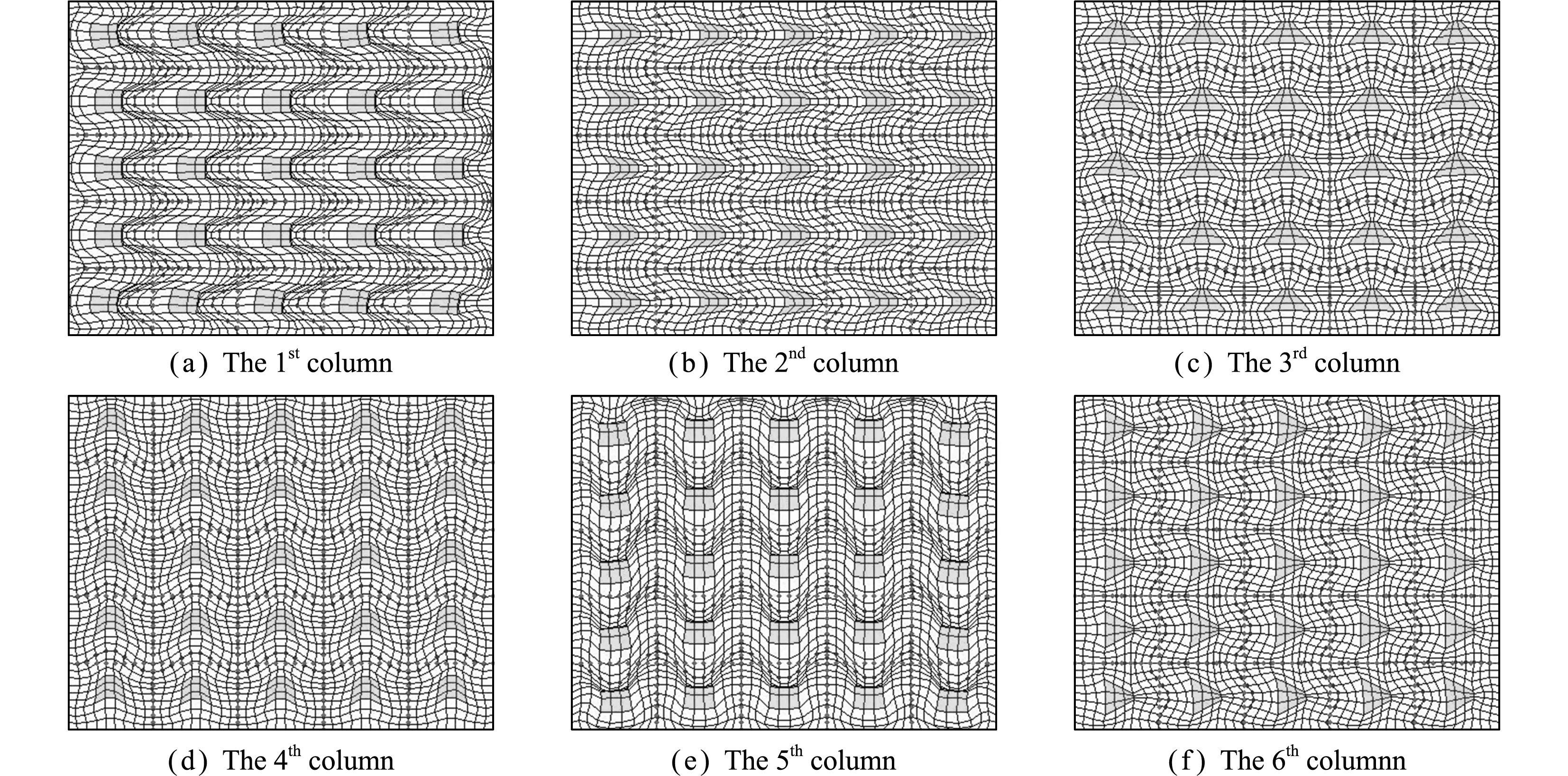
图10 使用超单胞周期边界条件得到的二阶虚拟位移2结构变形

(1) 使用超单胞周期边界条件得到的虚拟位移结构变形图和真实边界条件得到的虚拟位移结构变形图差异较小。

(2) 超单胞周期边界条件与真实单胞边界条件相似，可以有效处理数学均匀化方法单胞问题。

3.3 虚拟势能泛函

为了从数值上直观反映超单胞周期边界条件的计算精度，提出了与虚拟位移或虚拟载荷相对应的虚拟势能泛函Π的概念，其计算公式如下，

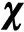
Πk l p=Uk l p+Wk l p

(10)

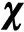
表2和表3分别给出一阶和二阶虚拟势能泛函的数值，其中ΠFEM表示使用真实单胞边界条件(方法1)计算得到的虚拟势能泛函，在此作为标准检验四边固支周期边界条件和超单胞周期边界条件的计算精度，Π1为使用四边固支周期边界条件(方法2)计算得到的虚拟势能泛函，Π2为使用超单胞周期边界条件(方法3)计算得到的虚拟势能泛函，从表2和表3的数值结果可以得到，

表2 对应一阶虚拟位移的虚拟势能泛函(107J)

表3 对应二阶虚拟位移/载荷的虚拟势能泛函(107J)

(1) 二阶虚拟位移计算误差要远大于一阶虚拟位移，即随着虚拟位移阶次的提高，无论施加何种单胞周期边界条件，计算误差都随之增大。

(2) 使用四边固支边界条件计算一阶虚拟位移的误差较小，而二阶虚拟位移计算误差过大。

(3) 使用超单胞周期边界计算虚拟位移的误差大幅降低，说明超单胞周期边界条件可以有效提高数学均匀化方法高阶虚拟位移的计算精度。

3.4 数值算例分析

为了验证上文分析结果的正确性，使用双线性平面单元，在图1结构中沿坐标x1方向施加面载荷f=0.1 MPa，每个单胞分为9×9个单元。为了方便研究单胞边界条件对数学均匀化方法计算精度的影响，均匀化宏观结构单元尺寸与单胞结构单元尺寸相同，均为1 mm×1 mm。

对四边固支的二维周期复合材料结构分别使用上文中的三种边界条件进行计算。

(1) 将整个结构作为一个大单胞进行处理，此时的单胞边界条件与结构边界条件相同，小参数ε=1，没有引入周期边界条件所带来的误差。

(2) 对单胞施加四边固支周期边界条件求解虚拟位移，值得注意的是，此时单胞单元的尺寸扩大5倍为5 mm×5 mm，小参数ε=1/5。

(3) 使用超单胞周期边界条件求解虚拟位移，此时超单胞内的单元尺寸仍然扩大5倍为5 mm×5 mm，小参数ε=1/5。

使用这三种方法计算分别得到图1中4条纵线A(穿过夹杂内部)、B(沿着单胞边界)、C(沿着基体和夹杂交界线)和D(穿过基体)上的节点真实位移曲线，结果列入表4，其中FEM为有限元细网格计算结果，作为标准检验三种单胞边界条件的计算精度，MsAEM1表示包含一阶摄动项的节点真实位移，MsAEM2表示包含二阶摄动项的节点真实位移，表5给出了势能泛函的计算结果，计算公式为

(11)

由表4和表5的数值计算结果对比可以得到,

表4 沿着纵线A，B，C和D节点的真实位移曲线Tab.4 Actual displacements comparisons of line A,B,C and D

(1) 使用方法2，即四边固支边界条件得到的节点宏观位移精度较差，根本原因在于四边固支导致单胞边界上的节点虚拟位移为0，即摄动位移为0，此时的节点宏观位移就是均匀化位移；MsAEM2的精度在单胞内部较低，主要是由于二阶虚拟位移计算精度较差。

(续表)

(2) 使用方法1和方法3得到的包含二阶摄动位移的节点宏观位移计算精度较高，也验证了文献[22]二阶摄动项必要性的结论。

(3) 方法1和方法3的计算结果十分相近，说明超单胞周期边界条件很好地反映了单胞在结构中的真实边界条件，可以有效地处理数学均匀化方法中的单胞边界问题。

4 结论

详细研究了数学均匀化方法单胞边界条件计算精度的问题，将影响函数作为虚拟位移得到了周期结构内单胞的真实边界条件，并提出了与之相应的虚拟载荷和虚拟势能泛函的概念，得到结论如下。

(1) 固支周期边界条件不适合作为二维结构单胞边界条件。

(2) 提出超单胞周期边界条件，大幅提高了二维周期复合材料结构数学均匀化方法的计算精度。

(3) 使用虚拟势能泛函验证了不同边界条件和摄动阶次对结构宏观位移计算精度的影响，进一步确定了二阶摄动项对数学均匀化方法计算精度的必要性。