基于冗余度与易损性的结构抗震能力提升方法研究

朱南海， 李杰明

(江西理工大学 土木与测绘工程学院，赣州 341000)

1 引 言

当前结构设计采用的是一种基于承载能力极限状态与正常使用极限状态的构件截面设计方法，基于此方法设计的结构未考虑各种因素影响导致的结构刚度下降。结构在非预期荷载作用下，某些构件产生初始损伤易使结构产生不成比例的破坏。文献[1]提出了结构构件在设计时应差别对待，构件承载力储备应具有层次性和差异性。重要构件在荷载作用下是结构关键构件的同时也可能是结构的薄弱易损部位所在，其破坏后对结构整体性能影响较大，故需重点关注此类构件，然而如何准确评估构件在结构中的重要性是当前急需解决的问题。冗余度是结构鲁棒性的重要组成部分，反映了结构在突发荷载作用下产生的局部损伤，其可形成备用传力路径的能力[2]；构件易损性则表明了在外荷载作用下，结构构件发生破坏的容易程度[3]。

目前，针对国内外对结构构件的重要性评价方法从多角度进行了研究。Frangopol等[4]早期提出将结构超静定次数即未知反力与已知平衡方程个数之差,作为冗余度的定义。Pandey等[5]基于结构对损伤杆件灵敏度的反比作为构件冗余度评价指标，在此基础上叶继红等[6-8]以结构构件应变敏感性响应作为构件冗余度评价指标，并以地震台试验验证其准确性。任伟新等[9]基于结构应变能变化提出了结构冗余度、鲁棒性及易损性评价指标。徐颖等[10]以构件内力灵敏度提出了单层球面网壳结构构件重要性评价指标。丁北斗等[11]以杆件内力变化与结构应变能响应作为结构构件重要性评价指标，并通过实验验证其准确性。蒋淑慧等[12]基于冗余度理论提出了杆系结构构件的重要性评价方法，并定量评价了结构的鲁棒性。柳承茂等[13]基于构件在结构中的刚度贡献作为重要性评价指标，并通过最小势能原理证明其准确性。文献[14]以损伤构件对其他构件及结构性能的影响作为结构构件冗余度及易损性的评价指标，并通过适当削弱结构高冗余-低易损构件，同时加强低冗余-高易损构件，实现了结构非重要构件先于重要构件发生破坏。文献[15,16]基于结构承载力变化量与原结构承载力比值作为结构构件重要性系数评价指标，并通过降低构件易损特性或构件的重要性，提升结构的鲁棒性。文献[17-18]基于广义结构刚度作为结构构件的重要性评价指标，实现了结构构件承载力安全储备的合理分布。

本文基于结构构件应变能对材料弹性模量的敏感性及其失效后结构应变能的变化量，建立了地震作用下结构构件冗余度及易损性评价指标。在此基础上将结构构件划分为四类，通过加强结构低冗余-高易损构件，同时适当削弱高冗余-低易损构件，调整结构构件截面面积，有效提升了结构的整体性能和抗震性能。

2 地震作用下的结构弹性响应敏感性

在地震作用下，结构的动力有限元方程可表示为

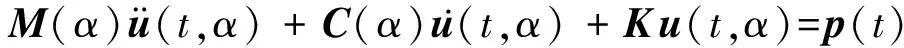
(1)

工程中采用的阻尼通常为Rayleigh阻尼模型，可表示为

C=w1M+w2K

(2)

式中w1和w2分别为质量阻尼系数和刚度阻尼系数。

式(1)等号两边分别对结构设计参数α求导并移项可得

(3)

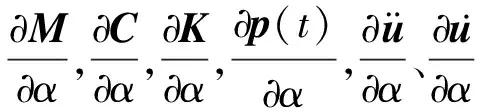
式(2)等号两边分别对结构设计参数α求导可得

(4)

将式(4)代入式(3)，可得

(5)

假设结构设计参数α为构件i的弹性模量Ei,则式(5)可写为

(6)

由于结构质量矩阵M及作用在结构上的外荷载p(t)与构件i的弹性模量Ei无关，则式(6)可写为

(7)

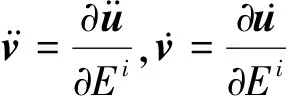
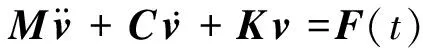
(8)

式中

(9)

F(t)为结构等效外荷载，∂K/∂Ei为结构刚度敏感性矩阵。式(9)与式(1)相似，以Newmark方法求解式(9)，可得到结构的加速度、速度和位移对构件i弹性模量Ei的响应敏感性。

根据应变能与节点位移的关系，t时刻构件j的应变能Sj i(t)可表示为

(10)

3 结构构件冗余度评价指标

根据Pandey等[5]提出的构件冗余度与其响应灵敏度成反比的定义，即

(11)

假设t时刻构件i产生初始损伤，则其对构件j的应变能影响可表示为Sj i(t)，综合考虑构件i的刚度发生扰动后对各构件的影响可表示为

(12)

式中ne为结构构件数，Sj i(t)表示t时刻构件i损伤时对构件j的应变能影响，αi越大则表明构件i产生初始损伤对结构整体性能的影响也越大。

构件破坏后，结构应变能变化量可直接体现其失效后对结构整体性能的影响，构件越重要，其破坏后结构应变能变化量越大，故可将构件i破坏后结构应变能变化量与原结构应变能的比值作为衡量其在结构的重要程度，可表示为

(13)

综合考虑构件i失效后对结构各个构件应变能及整体性能产生的影响，将构件i的冗余度定义为

(14)

式中ERi为构件i的冗余度指标，冗余度指标值越小，表明该构件i失效后对结构及其余构件产生的影响越大。

4 结构构件易损性评价指标

在荷载作用下，结构破坏过程实质是结构刚度退化累积的结果，而结构刚度下降是由于构件刚度不断退化导致的。在荷载作用下，结构各构件刚度退化程度有所不同，若构件r对自身或其余构件刚度变化比较敏感，则其刚度下降较快，当其累积到一定程度时，构件r必先破坏。

冗余度是鲁棒性的重要组成部分，而易损性是鲁棒性的相反概念，根据式(11)冗余度与敏感性成反比可知，易损性与敏感性成正比关系。本文以构件弹性模量作为刚度参数，当t时刻构件n产生初始损伤，构件r的灵敏度可由式(10)表示。综合考虑各构件及自身刚度发生变化时的敏感性，将构件易损性表示为

(n=1,2,3,…,ne)(15)

式中t时刻Sr n为构件r的应变能cr对构件n的弹性模量En的灵敏度。式(15)用于衡量结构各构件产生初始损伤时对构件r产生的影响，EVr越大表明构件r对结构刚度变化越灵敏，也越易损。

5 结构抗震能力的提升措施

根据式(14,15)计算得到结构构件冗余度和易损性指标，将结构构件划分为高易损-低冗余构件、高易损-高冗余构件、低易损-低冗余构件和低易损-高冗余构件四类[14]。高易损-低冗余构件是结构的关键构件也是结构中薄弱易损部位，其破坏后将对结构产生较大的影响甚至引起结构整体性倒塌破坏，而低易损-高冗余构件为结构的一般构件，其失效后对结构影响较小。因此,可加强高易损-低冗余构件，适当削弱低易损-高冗余构件，从而有效提升结构整体性能和抗震性能，其流程如图1所示。

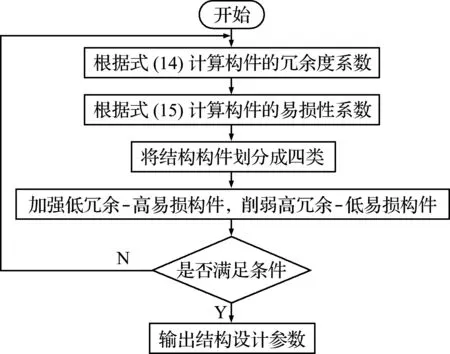
图1 结构抗震能力提升优化流程

6 算例分析

6.1 6层钢框架结构

如图2所示的一榀六层三跨平面钢框架，跨度均为6.0 m，层高均为3.6 m，钢材的弹性模量为210.0 GPa，密度为7.85×103kg/m3，屈服强度为235.0 MPa。框架为8度抗震设防，场地类别为第1组II类，结构每层重力荷载为梁均布荷载 40.7 kN/m。结构各层梁、柱均为H型截面，梁截面均采用400 mm×200 mm×9 mm×12 mm，柱截面均采用450 mm×450 mm×10 mm×14 mm。

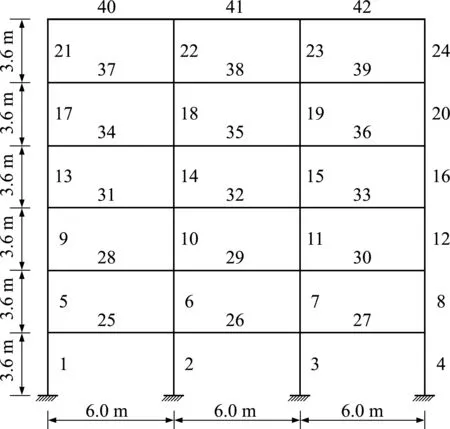
图2 钢框架平面布置

结构由重力荷载标准值及多遇地震标准值共同作用，而结构可能遭受向左水平地震作用或向右水平地震作用，故对结构分别施加向左水平地震及向右水平地震得到两组数据，将两组数据对比并取每根构件冗余度较小值或易损性较大值，结构各构件冗余度及易损性如图3和图4所示。可以看出，底层中柱(2号和3号构件)的易损性数值较大，其次是底部第2层中柱(6号和7号构件)，说明整个结构的薄弱部位为底层中柱。对于梁而言，边梁的冗余度要小于跨中梁，其原因是边梁对边柱的侧移有着极强的约束，其失效后边柱失去横向约束成为长柱，使柱的承载力严重降低，而跨中梁失效后，中柱有着边梁的约束，对柱的影响小一些，故其失效后对结构的影响小于边梁。总体而言，柱的冗余度较小，梁的冗余度远大于柱，中柱小于边柱。柱的易损性随着层高逐渐降低，而梁的易损性整体上远小于柱，底层柱的冗余度小于上层柱，且底层柱的易损性大于上层柱，因为在地震作用下，柱要抵抗侧力和竖向力作用，柱承担的竖向荷载与其所在楼层有关，所在楼层越小，其竖向荷载越大。直观上，柱失效后产生的影响大于梁，结构构件冗余度和易损性的分析结果也说明了在多遇地震作用下，柱的冗余度远小于梁，而易损性则远大于梁。因此，2号柱、3号柱、6号柱和7号柱为结构的薄弱易损部位，亦为结构的关键构件，而由于梁的冗余度普遍较大，易损性系数较小，为结构的一般构件。

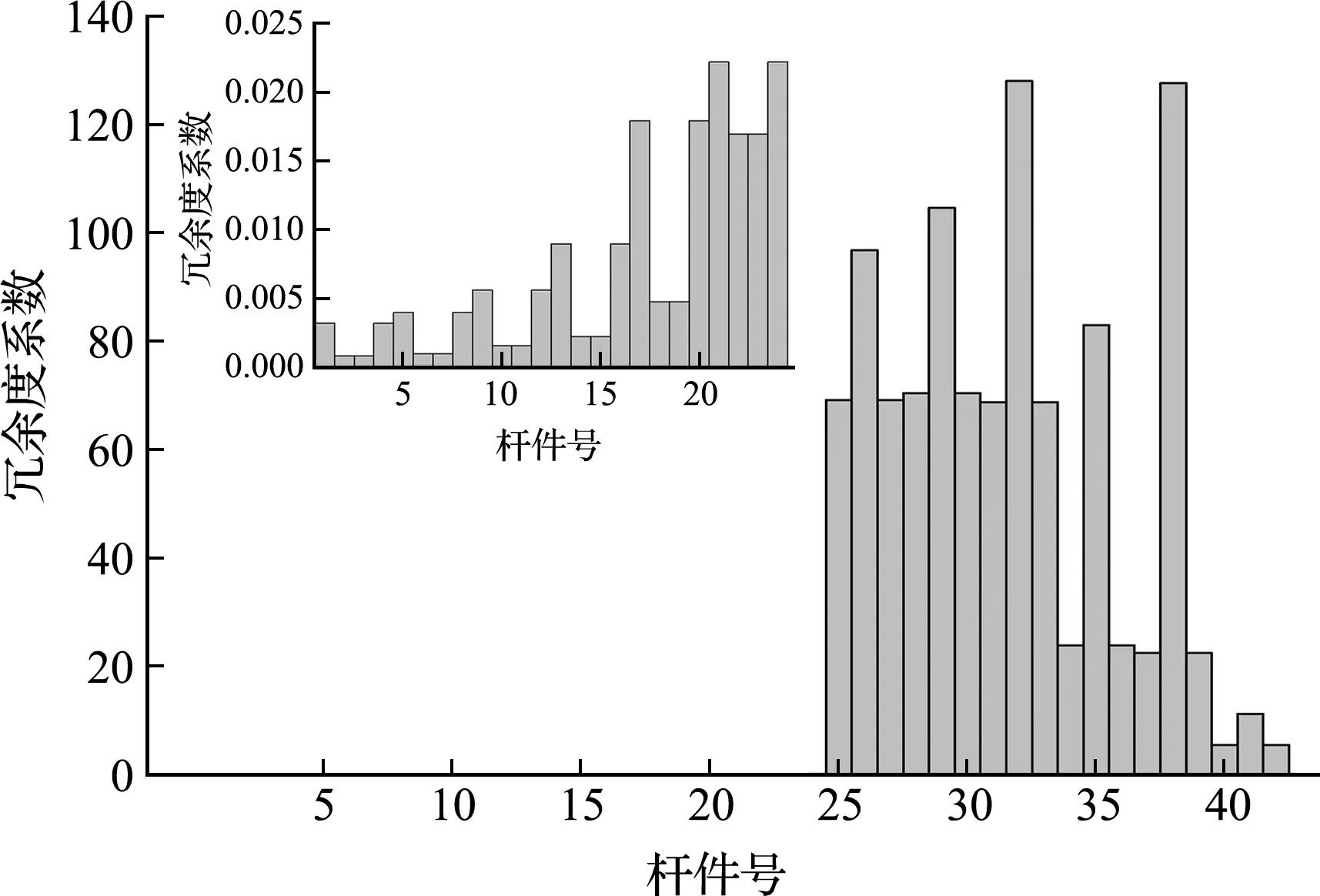
图3 钢框架各构件的冗余度系数分布

图4 钢框架各构件的易损性系数分布

为使结构在地震作用下的安全性能得到更好的保证，将结构中的关键构件进行适当加强，同时削弱一般构件。在控制结构材料用量的情况下，将构件2、构件3、构件6和构件7的截面调整为 450 mm×450 mm×11 mm×15 mm，而梁截面调整为450 mm×200 mm×7 mm×12 mm。图5和图6为杆件面积调整后各杆件的冗余度系数与易损性系数，由此可知结构柱的冗余度有所上升，梁的冗余度有所下降；杆件6和杆件7的易损性有所下降。图7为结构在8度罕遇地震作用下，结构构件截面调整前后的各层最大层间位移角。可以看出，面积调整后结构最大层间位移角明显下降，其最大层间位移角值由0.00154下降到0.00141，下降了8.4%，结构变形更加均衡。分析结果表明，根据结构构件的冗余度和易损性，加强结构薄弱易损部位，合理削弱一般构件，可以使结构的层间变形更加均匀，结构刚度、抗震性能及变形能力得到有效提升。

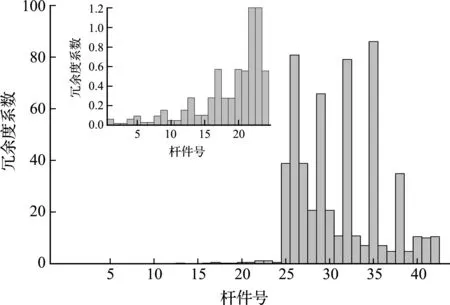
图5 截面调整后钢框架各构件的冗余度系数分布

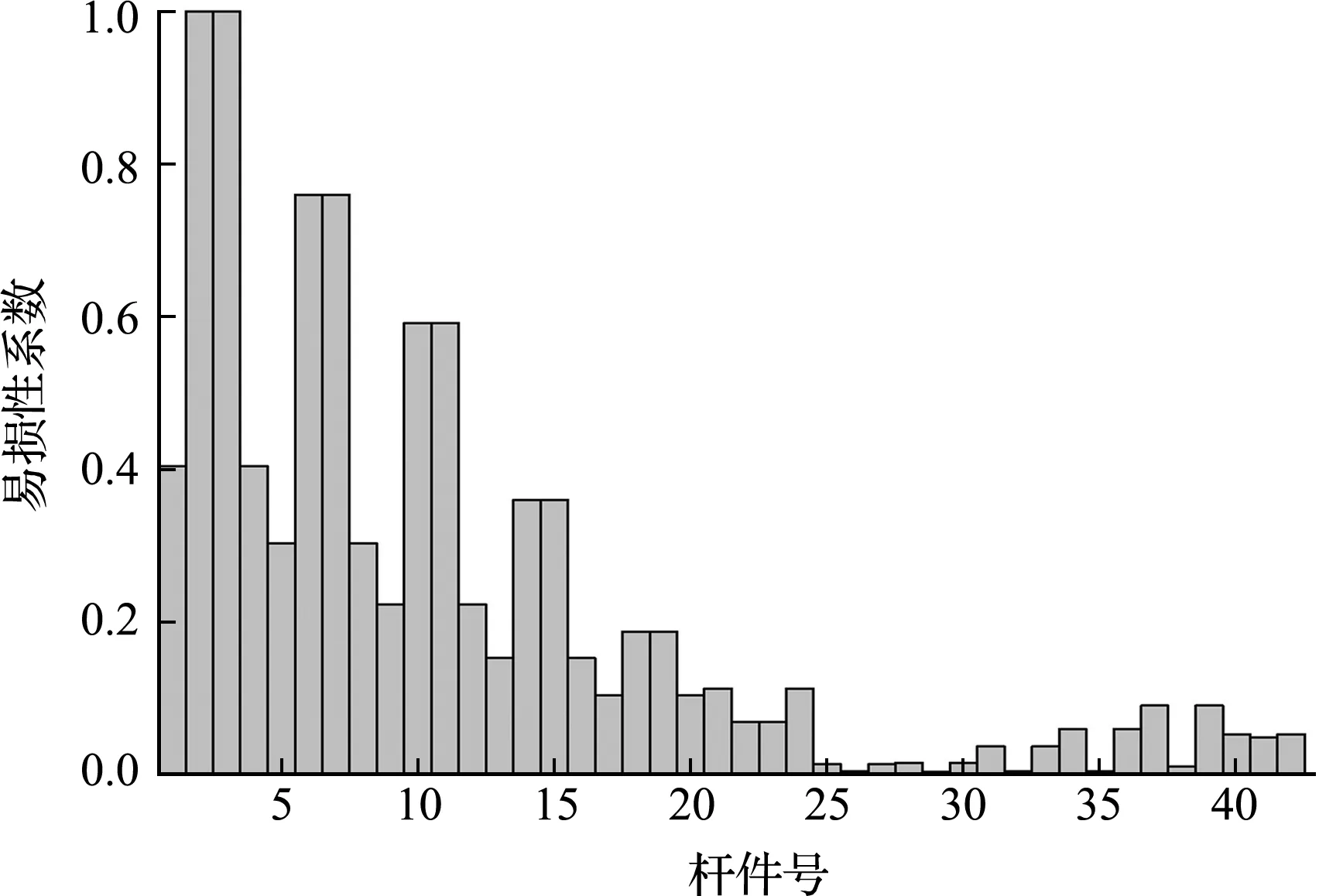
图6 截面调整后钢框架各构件的易损性系数分布

图7 结构层间位移角

6.2 K6N3单层球面网壳结构

如图8所示的K6型单层球面网壳结构，跨度为20.0 m，矢高为4.0 m，周边固定支座，节点为刚性连接，结构为8度抗震设防，场地类别为第1组II类，构件均采用Q235钢管，弹性模量为 210.0 GPa，密度为7.85×103kg/m3，泊松比为 0.3，杆件屈服强度为235.0 MPa，节点等效荷载为3.5 kN，各构件的应力和结构位移均满足设计要求。根据结构构件的空间位置，将构件分成5组如图9所示，各组杆件面积列入表1。

图8 K6N3单层球面网壳结构

图9 K6N3单层网壳结构构件分组

表1 截面调整前后K6N3单层球面网壳结构各分组构件的截面面积

根据式(14，15)得到结构各构件的冗余度和易损性系数分布分别如图10和图11所示。可以看出，底层构件的冗余度总体上小于上部杆件，下部结构构件易损性高于上部结构构件。其原因是在地震作用下，底层构件承受结构上部传递的竖向荷载及横向荷载，这些构件是结构的重要构件，其破坏后对结构有着重要的影响，甚至会使结构出现倒塌破坏，而顶部构件冗余度系数数值较大，易损性系数数值较小，其破坏后对结构影响较小，为结构的一般构件。

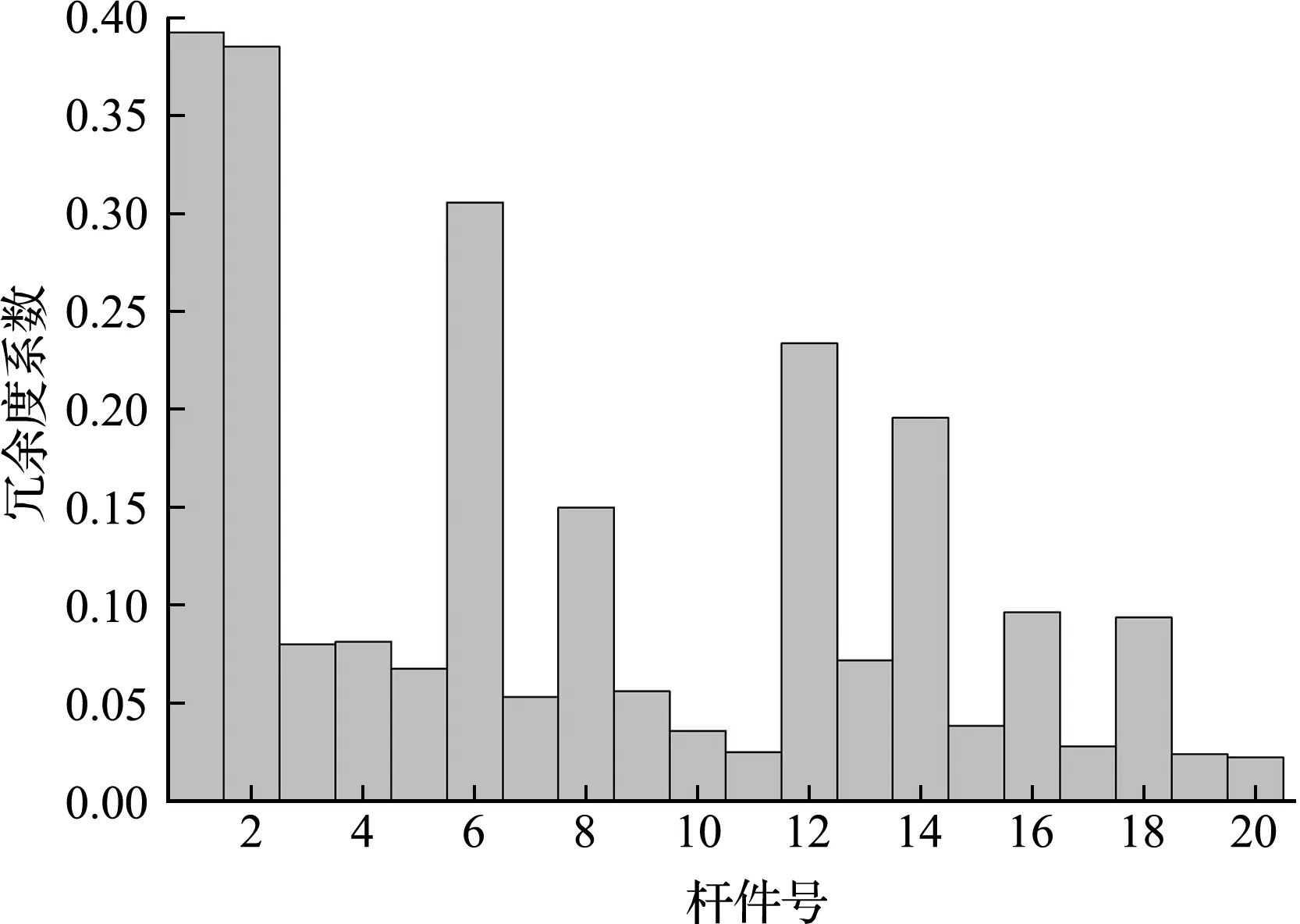
图10 K6N3单层球面网壳结构各构件的冗余度系数

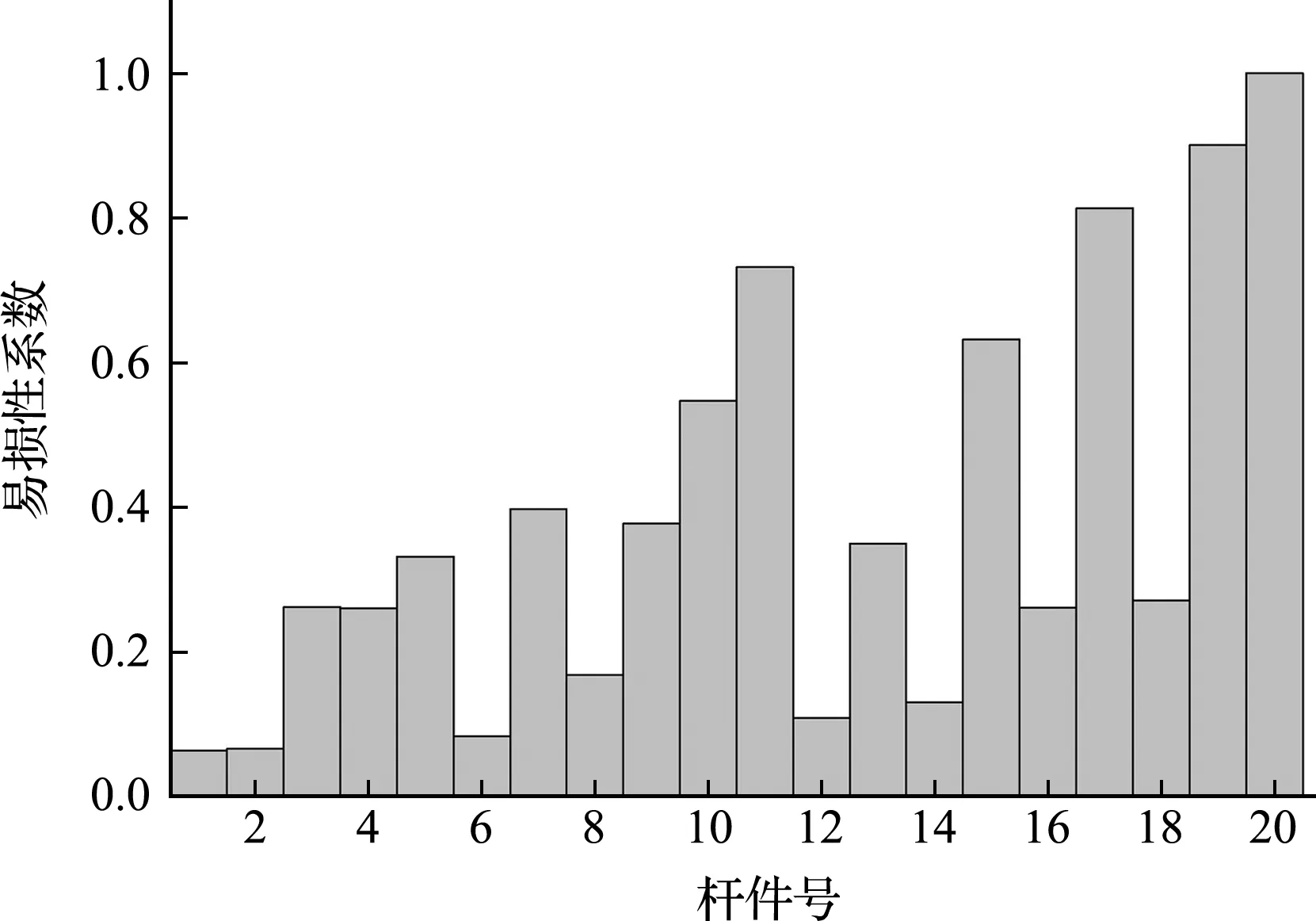
图11 K6N3单层球面网壳结构各构件的易损性系数

同理，控制结构材料用量，增强该网壳结构中的低冗余-高易损构件，削弱高冗余-低易损构件，截面调整后各组构件的截面面积列入表1，由此可知第5组构件面积从11.49 cm2增加到12.15 cm2，而第1组和第2组构件面积由11.49 cm2减小到 9.33 cm2，降低了13.84%。

图12和图13为杆件面积调整后各杆件的冗余度系数与易损性系数，可以看出，结构第1组和第2组的构件，即构件1～4的冗余度系数明显下降，而其易损性系数则有所提高。

图12 截面调整后K6N3单层球面网壳结构各构件的冗余度系数

图13 截面调整后K6N3单层球面网壳结构各构件的易损性系数

通过对结构输入El-Centro地震波，并逐级提升地震加速度峰值，得到结构地震加速度峰值-最大节点位移曲线(图14)以及地震加速度峰值-杆件屈服比例曲线(图15)。可以看出，随着地震加速度峰值的不断增大，原结构杆件屈服比例不断上升，结构位移不断增大，结构在地震加速度峰值为1020 gal时杆件屈服比例达到42.17%，节点最大位移为0.1317 m，网壳破坏模式为动力失稳破坏。截面调整后，结构抗震性能有明显提升，在地震加速度峰值1120 gal时网壳构件屈服比例达到47.39%，节点最大位移为0.1219 m。同理上述算例分析表明，根据构件冗余度和易损性评价指标，调整结构关键构件及一般构件的截面面积，可以充分发挥构件在结构中的作用，使得结构刚度退化过程有所延长，网壳结构抗震性能有明显提高。

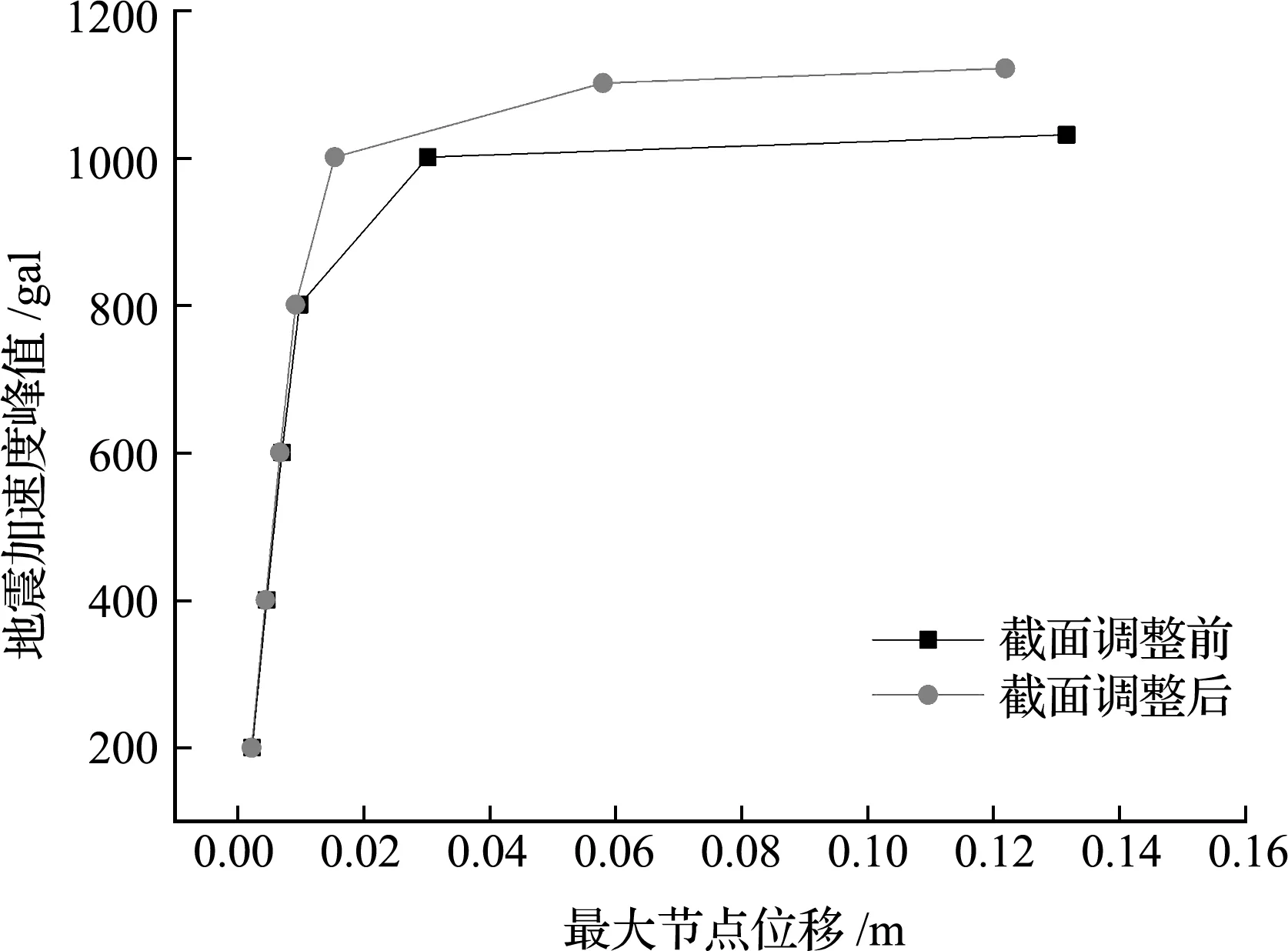
图14 地震加速度峰值-最大节点位移曲线

图15 地震加速度峰值-屈服杆件比例曲线

7 结 论

本文基于结构构件应变能对材料弹性模量的响应敏感性及其失效后结构的应变能变化量，建立了结构构件冗余度及易损性评价指标以反映其在地震作用下的冗余特性及易损属性。而后将结构构件分为四类，通过加强高易损-低冗余构件，同时适当削弱低易损-高冗余构件，调整构件截面面积，可有效提升结构的整体性能和抗震性能。主要结论如下。

(1) 基于结构构件应变能对材料弹性模量的响应敏感性及其失效后结构应变能变化量，建立了地震作用下结构冗余度及易损性评价指标，可以准确反映其在结构中的重要程度及其发生破坏的容易程度。

(2) 根据结构构件的冗余度及易损性将结构构件划分为四类，通过加强高易损-低冗余构件，同时适当削弱低易损-高冗余构件，可实现结构整体性能和抗震性能的有效提升。