单元主题教学下《圆的面积》教学设计与思考

文|郝晓鑫 宋美辰

部分教师习惯采用“课时教学”的形式进行备课上课，这样的形式，便于教师“吃透讲透”某一节课，发挥教学活动的最优化作用。但是，单一的课时教学割裂了单元知识的整体联系，使知识变得碎片化，不利于学生系统化知识框架的建立，容易导致学生相对狭隘的知识视野，不利于培养学生的整体思考能力。相比较于课时教学，单元教学有着显著的优势，它打破课时之间的界限，站在单元这一高层面上整合知识，借助各种探究手段，发挥知识迁移作用，促进学生理解知识，最终指向学生数学核心素养的培养和提升。

【教学过程】

环节1：开门见山，明确圆面积的概念。

师：圆将平面分成三部分，圆内、圆上和圆外。圆内区域的大小就是圆的面积。圆虽是一个曲边图形，但有精确计算其面积的公式——S=πr2。这节课我们来研究、探讨圆的面积公式，思考如何借助各种知识得到圆的面积公式。

【设计意图：帮助学生明确圆面积是圆内区域的大小，这是研究圆面积计算方法的前提。此外，课前的学情调研也表明，大多数学生知道圆的面积公式，能够说出S=πr2，但是，圆的面积公式是如何推导出来的，大多数学生是一知半解的。因此，在导入环节开门见山的将圆的面积公式告诉学生，引导学生关注如何借助学过的知识推导出圆的面积公式，突出本节课的重点。】

环节2：估算探路，确定圆面积的范围。

师：在推导圆面积公式前，我们通过估算圆面积来初步验证圆面积公式的合理性。

【设计意图：学生具备估算的意识和能力是课程教学的目标；同时会估计给定图形的面积是《数学课程标准（2011年版）》中的具体要求。在确定一个数学结论时往往先是通过估算进行初步判断其合理性，然后再进行严格推理。因此，在推导圆面积公式前，通过估算探路是理论要求和教学实际的需要。】

师：圆面积公式S=πr2，它是圆周率π 和r2的乘积。r2会让你联想到哪个图形的面积呢？你能在圆中画出来吗？

生：用圆规画圆，半径标注为r。在圆中画出正方形。（如图1）

图1

师：正方形面积和扇形面积的大小关系是什么？

生：扇形的面积小于正方形的面积。

师：你能构造一个已经学过的，并且其面积小于扇形面积的图形吗？请在图中画出来。

生：我在扇形中画出了直角三角形。（如图2）

图2

师：圆可以分成这样的4 组（如图3），请结合圆外切正方形和圆内接正方形计算圆面积的范围。

图3

生：直观看出圆外切正方形的面积＞圆的面积＞圆内接正方形的面积。通过计算得出4r2＞圆的面积＞2r2。

师：通过公式求出的圆面积是否在此范围中呢？

生：因为4＞π＞2，所以4r2＞πr2＞2r2，这与直观观察的结果是一致的，因此初步判断圆面积公式是合理的。

【设计意图：古代数学家曾用圆外切正多边形和圆内接正多边形的面积无限逼近圆的面积，而“方中圆”和“圆中方”是研究圆面积过程中化曲为直、无限逼近的雏形。将圆外切正方形和圆内接正方形生成的过程展现出来，能够加深学生对它们的理解，为后续进一步研究圆的面积打下基础。】

环节3：多措并举，无限逼近圆的面积。

师：六边形ABCDEF 是圆内接正六边形，分别取弧AB、BC、CD、DE、EF、FA 的中点，依次标记为A1、B1、C1、D1、E1、F1，依次连接这些顶点形成圆内接正12 边形。（如图4）

图4

师：圆内接正六边形的面积和正12 边形的面积相比较，大小关系如何？

生：圆内接正12 边形的面积大于正六边形的面积。

师：请你想象一下，通过这样不断地取弧的中点，构成圆内接正24 边形、圆内接正48 边形……它们的面积会有怎样的变化？与圆面积的大小关系如何？

生：当圆内接正多边形的边数增加时，正多边形的面积也随着增加，其面积也更加接近圆的面积。

师：古代刘徽的割圆术就是增加圆内接正多边形的边数，用正多边形的面积去逼近圆的面积。现在将圆内接正多边形逼近法用组图的形式展现给大家（如图5～7）。

图5 圆内接正六边形

图6 圆内接正12 边形

图7 圆内接正18 边形

师：下面请大家创造新的逼近方法，用组图形式表达自己的想法。

方法一：三角形逼近法（如图8～10）。

图8

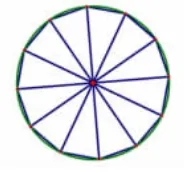
图9

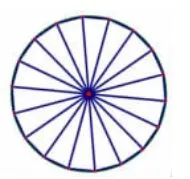
图10

方法二：正方形网格逼近法（如图11～13）。

图11

图12

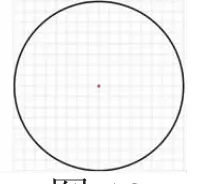
图13

方法三：增添法（如图14～16）。

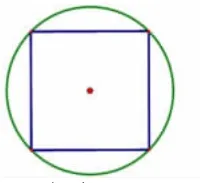
图14

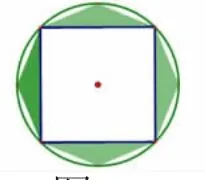
图15

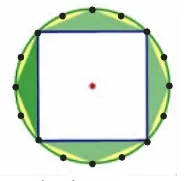
图16

师：刚才大家通过不同的方法逐步逼近圆的面积，逼近的过程一直持续下去就会得到圆面积的精确值。

【设计意图：直观展示出圆内接正多边形的面积随着边数的增加而增加，不断引导学生体会正多边形的边数越来越多时，它的面积也就越接近圆的面积，渗透极限思想。同时，展示多种不同的“割圆”方法，鼓励学生尝试不同方法进行分割，体现算法的多样化。此外，简单介绍我国数学家刘徽及其数学成就，渗透数学文化。】

环节4：新旧衔接，推导圆面积的公式。

师：圆面积公式S=πr2能帮助我们精确求出圆面积，我们除了知道圆面积公式是什么，还需要探索其推导过程。大家对于面积公式的推导有什么经验？

生：之前学习平行四边形和三角形面积时，是将新图形转化成已经学过的图形进行推导的。

师：那圆的面积能否转化成我们学过的图形呢？大家尝试利用以下两套学具将它们近似地转化成已经学过的图形。学具一是平均分成12 个扇形的圆形纸片（如图17）。学具二是用圆环拼成的圆面（如图19）。

图17

方法一：利用等分成12 个扇形的圆形纸片转化成平行四边形（如图18）。

图18

图19

师：怎么能让转化成的图形更像平行四边形呢？

生：当等分的份数越来越多时，扇形的曲边就越接近直边，拼出来的图形就越像平行四边形。

师：当等分的过程一直进行下去，拼出来的图形就会变成平行四边形。

方法二：沿着圆面的一条半径剪开，将圆环拼成的圆面转化成三角形（如图20）。

图20

环节5：举一反三，圆面积公式的运用。

题目一：如图21，有一个直径为20 米的圆形花坛，要在花坛内种植4 种花，每种花种植的面积是多少？（解答略）

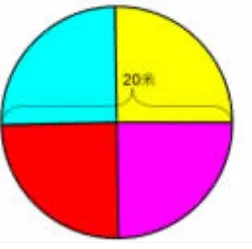
图21

题目二：如图22，一个半径为10 米的圆形草坪，准备在草坪中一个半径为8 米的圆形区域内种植鲜花，求剩余草坪的面积是多少？

图22

生：先计算出圆形草坪的面积S=πr2=3.14×10×10=314（平方米）；再计算出鲜花的占地面积S=πr2=3.14×8×8=200.96（平方米）；最后计算剩余草坪的面积314-200.96=113.04（平方米）。

【设计意图：巩固圆面积公式的同时，对接了扇形面积和圆环面积。】

【教学思考】

1.单元主题教学的优势在圆的面积中的两点体现。

其一，圆面积推导逻辑更合理。在圆面积的推导过程中，课本编排将圆分割成一些完全相同的扇形，但是学生在此之前并没有接触过扇形，扇形的学习被安排到了圆面积之后进行学习。而单元主题教学就是鼓励教师打破原有的知识顺序，重新构建知识体系。因此将扇形的认识放在了圆面积教学之前。

其二，圆面积推导方式更丰富。此外，课本中只安排了将圆分割成扇形这一种方式来推导圆面积公式，而将圆分割成圆环也是圆面积公式推导的一种方法，多种方式去探究圆面积公式的由来有助于加深学生的理解，拓展学生的思维。但是课本中圆环的学习安排在圆面积之后。因此，利用单元主题教学的思路，将圆环的初步认识提前学习。

2.如何在圆面积教学中为小学生渗透极限思想。

极限是一个固定的数，它是无限逼近的终点。利用圆面积公式求出的数是圆面积的精确值，也就是无限逼近的极限值。在环节一中就明确指出了这一点。

学生理解极限的前提是理解无限，而在圆面积公式的探索过程中，学生所做的操作都是有限的，将这个分割的过程无限地进行下去需要学生去想象，这正是极限思想的难点所在。要想让学生初步感受极限思想，就要让学生多次想象无限逼近的过程。环节3 通过不同的方法逼近圆的面积，每种方法后都提到当这样的操作过程一直持续下去时它们的面积就会等于圆的面积。在环节4中，圆要转化成平行四边形和三角形，由“像”到“是”的过程，就是从“有限”到“无限”的过程。

（“第十三届小学教学特色设计大赛”获奖作品选登）