连续时间下政企共同运作基建的博弈分析

中国农业银行福建省分行 余润堃

一、研究背景

PPP是近年来我国新兴的基础设施建设模式，该项目的特点是政府与企业通力合作，通过资源互补实现共同提供公共产品。该运作模式的主要优势在于政府的资金短缺问题可以得到有效解决，极大地减轻地方政府的财政压力。但是，政企共同运作基建时也存在资源浪费、偷工减料引发的巨大损失，最终都需要社会公众为损失买单。

在研究政企共同运作基建时，国外学者一致认为，政府在共同运作中要扮演好管理者的角色，尽到公共管理人的职责。萨瓦斯认为，PPP项目是政府通过合同承包、特许经营与补助等形式与企业共同参与公共服务的生产与安排过程。Samii认为PPP是政府和企业为实现可持续利益输出的创新型合作伙伴关系。Spielman 和 Von Grebmer指 出，PPP项目是政府与企业通过优势互补的手段，应用特定技术协同提供公共产品或服务以达到特定目标的一种合作制度。Ahmed认为，在PPP项目的实际分工当中，政府扮演维护公共利益并对企业进行监管的角色，企业负责提供公共产品与服务。Sabry的研究结果表明，PPP项目的绩效提高依赖于政府办事效率及监管水平的提高，在这种情况下，企业的投资水平也会随之增长。

二、模型假设

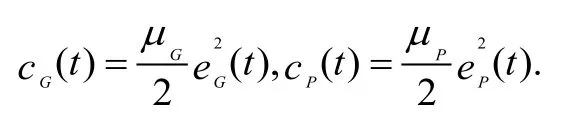
其中，μG和μP分别表示政府和企业在维护社会公众福利过程中付出成本的系数。在现实背景下，政府与企业的成本不为负数，故μG和μP的取值范围是(0,+∞)，则函数cG(t)和cP(t)都是关于各自努力水平的凸函数。

本文探讨的政府与企业的合作基础是社会公众福利W，其原因在于政府代表公众利益，其参与共同运作的出发点必然是社会福利，企业在参与共同运作时必须适当考虑社会公众福利，完全忽视社会福利将导致共同运作的失败[2]。故设变量W(t)∈(0,+∞)代表社会公众福利，采用随机微分方程刻画公众福利W(t)随时间变化的趋势：

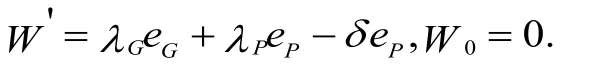
上述福利函数中，Gλ和Pλ分别表示政府和企业的努力水平对社会公众福利的贡献程度，Gλ和Pλ的取值范围是(-∞,+∞)。δ表示社会公众福利的衰减程度，其取值范围是(0,+∞)。在应用随机微分方程刻画公众福利变化趋势时，本文出于共同运作的实际情形，重点探讨政府与企业对社会福利的增益水平。考虑到实际政企的基建合作是以招投标的形式进行，且对企业的准入门槛要求较高，则资源过度竞争导致的社会公众福利衰减不适用本文所讨论的情景，因此将社会福利的损失一般归责于企业的不作为或者是投机行为。

假定πG(t)表示政府在t时刻的收益，πP(t)表示企业在t时刻的收益，π(t)表示政府与企业在t时刻创造的社会总收益：

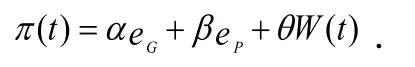
在上述函数中，α,,βθ均为大于0的常数，它们分别代表政府努力水平、企业努力水平、社会公众福利增益对整个PPP项目运营收益的影响水平。本文模型中的收益函数π(t)由eG、eP、W(t)三部分构成，是参考文献模型的演化。

TπG(t)表示政府在全部时间内的收益，TπP(t)表示企业在全部时间内的收益,PPP项目运营绩效在政府与企业之间分配，政府预先约定的分配比例为σ,其取值范围是(0,1)，则企业的分配比例为1-σ。η是控制变量，用来描述政府对企业的激励，其取值范围是(0,1)。政府与企业的贴现率r相同且为正。双方的意图都是在未来的无限时间内寻找使得自身利益实现最大化的最优努力策略，可将政府在无限时间内收益的目标函数表示为:

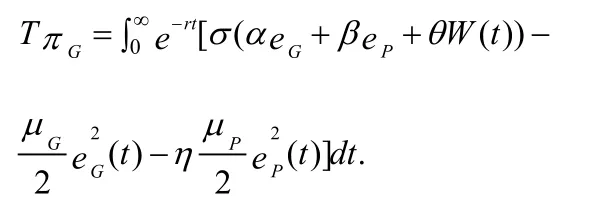
企业在无限时间内收益的目标函数表示为：

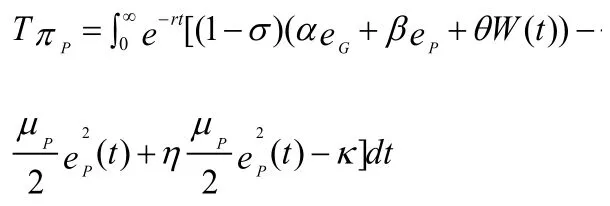
κ表示企业从金融机构拆借资金的成本，是结合本文背景考虑到企业在实际运作中可能出现的资金运作困难向金融机构拆借资金的情形，为本文对参考文献模型的改进。

在现行的政企共同运作基建的合作中，通常呈现以政府为主导的共同运作机制，政府一般在与企业的合作中扮演领导者的角色，企业也通常会根据政府的行动采取下一步策略。本文研究政府与企业由于地位不对等带来的决策次序不对等的情形，通过建立斯塔克尔伯格模型求解政府作为领导者情形下的双方最优努力水平与最佳收益。在得出最优努力水平与收益后进行算例仿真分析。

三、最优收益

子博弈是指在动态博弈中，所有参与人先后采取了一次行动后所构成的一组新的博弈，这组博弈中的每个策略组合都称为“子博弈”。当参与人在子博弈系列中的每一个子博弈都构成纳什均衡时，该情形称作子博弈精炼纳什均衡。在政府与企业的共同运作中，当政府采取对抗或是协作的策略时，企业会根据政府的行为作出相应的策略反应，此时双方的策略组合构成子博弈。为使每个子博弈都达成纳什均衡，需要进行策略的倒推演算。

政府将首先选择自有的努力付出水平及对企业的激励因子，企业在观察到政府的行为并且接收到其释放的讯号后，选择有利于自身的行为决策及资本结构。双方的博弈过程完全符合主从博弈的逻辑及过程。政府是博弈行为的领导者，企业是博弈行为的跟随者。为了得出斯塔克尔伯格模型的均衡结果，需要运用逆向分析法求解。

政府与企业的收益是关于时间的函数，且该函数与社会公众福利变量W(t)相关无法直接求解，结合参考文献用动态规划原理构造优化问题进行求解。

企业的连续有界微分最优收益函数对所有的W≥0满足优化问题：

政府的连续有界微分最优收益函数对所有的W≥0满足优化问题：

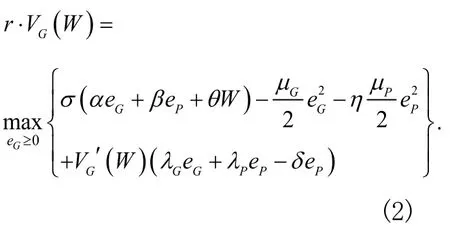
首先求解企业的最佳收益，对上述等式的右端部分求其对eP的一阶偏导数并令其为0，得如下结果：

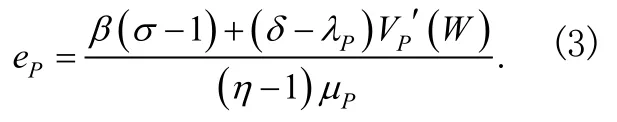
得到政府和企业最优收益函数，分别对W求导后得到的导数代入即可得政府和企业最优努力水平、政府最优激励系数如下：

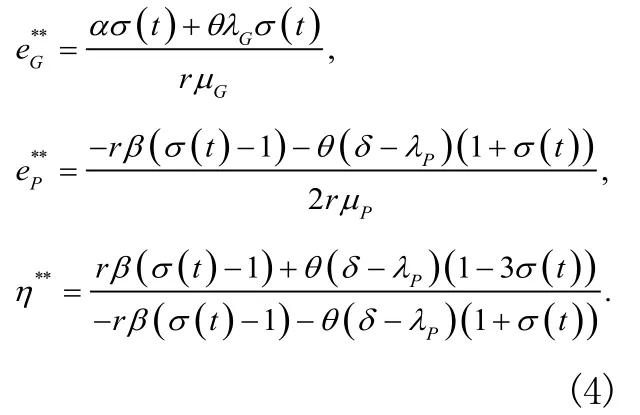
在实际的政企合作中，企业的收益显著受到政府对其好感程度的制约，同时也受到政府所关心的社会公众福利的制约。

四、数值仿真

以政府收益分配比例为自变量，最优收益为因变量，其他参数取定值作比较分析图。可设定时间t=1，衰减率δ=0.1，贴现率r=0.1，激励系数η=0.2，政府与企业付出的成本系数μG=1,μP=2，政府与企业的努力对社会公众福利的影响系数λG=1,λP=2，企业从金融机构拆借资金的成本κ=0.05，政企在时刻t=1组成的总收益系数θ=1,α=2,β=3。由上述参数设定值可以得到政企同时行动下政府最优收益、企业最优收益、社会最优收益关于政府收益分配比例的函数图像（见图1），其中σ∈(0,1)。

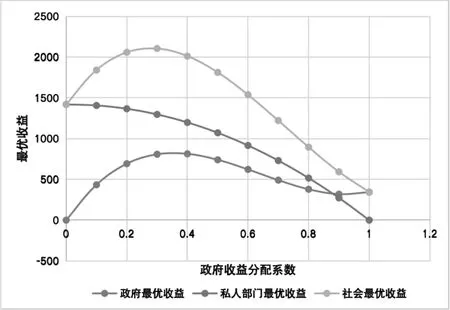
图1 最优收益关于政府收益分配比例函数图

以时间t为自变量，最优收益为因变量，其他参数取定值作比较分析图。可设定分配比例σ=0.4，衰减率δ=0.1，贴现率r=0.1，激励系数η=0.2，政府与企业付出的成本系数μG=1,μP=2，政府与企业的努力对社会公众福利的影响系数λG=1,λP=2，企业从金融机构拆借资金的成本κ=0.05，政企在t时刻组成的总收益系数θ=1,α=2,β=3。由上述参数设定值可以得到政企同时行动下政府最优收益、企业最优收益、社会最优收益关于时间t的函数（见图2），其中t∈(0,+∞)。

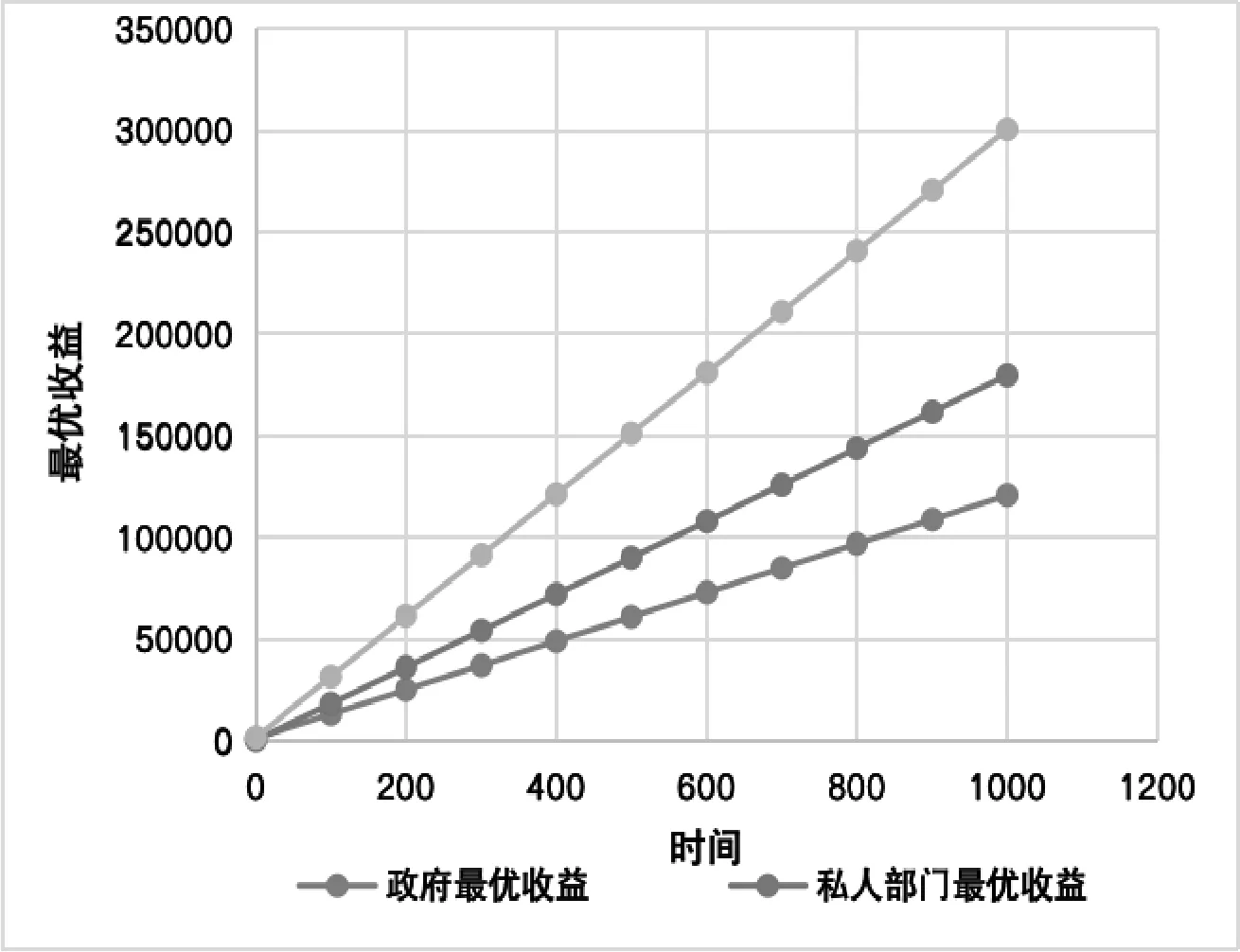
图2 最优收益关于时间函数图

五、管理启示

在主从博弈初期，政府的收益分配系数的高低与否对社会总体收益的增减几乎不产生影响，政府需要注意制定合理的收益分配系数，协调自身与企业的利益，使收益分配在遵循公平原则的同时能满足双方的需求。在项目长期运营的情况下，政府主导项目控制权的优势将显著显现出来，提示政府在实务中积极参与项目规则的制定，主动引导企业遵循规则并维护公众福利。企业在主从博弈下尽管在项目初期受到政府的管制较多，但从长期来看，与政府的关系将逐渐缓和，在长期共同运作下，企业要注意在遵守规则的同时适当发挥主观能动性，以创造更大的项目价值。