基于气味多物化特征的嗅感评价模型

苏仲端

（广东工业大学信息工程学院，广州 510006）

0 引言

嗅觉感知是嗅觉系统对气体分子进行加工编码的结果［1］，气味分子通过与嗅上皮不同的嗅觉受体进行特异性结合，将外界刺激转化为动作电位，经过神经网络传递给大脑。然而，生物嗅觉系统复杂的运行机制使嗅觉研究的进展缓慢，多年以来，我们无法通过一个给定的气味分子来预测该气味的味道。以洛克菲勒大学的Andreas Keller为领导的团队于2015年开展了一个名为“梦想嗅觉预测挑战赛”（The DREAM Olfaction Prediction Challenge）的比赛，其中官方给定了476种气味分子的4884种物理化学特征（简称物化）数据，49名志愿者提供的21种嗅觉感知（简称嗅感）评价，20多支参赛队伍运用各种机器学习算法对上述气味分子进行感知预测［1］。基于“梦想嗅觉预测挑战赛”，本文的思想是以476个单分子化合物的物化特征作为研究数据，以构建有效的气味物化特征空间和气味的嗅感评价模型为研究目的，通过特征选择和提取方法，确定适配不同嗅感评价的最佳特征空间，最终实现从气味特征空间到嗅感评价空间的映射，对实现理想的机器嗅觉感知系统具有重大理论指导作用。本文的研究内容如下：

（1）对获取的高维气味物化特征X进行降维，以21种嗅感评价作为目标y，采用特征选择方法（随机森林）和特征提取方法（PCA），形成不同的特征空间。

（2）基于岭回归（Ridge Regression）模型，对获取到的特征空间进行学习，得到嗅感评价结果。

（3）实验结果分析，对比回归模型应用于不同的气味特征空间的结果。

1 构建气味物化特征空间

1.1 数据预处理

本实验数据集分为两个，嗅感评价数据集和气味物化特征数据集，其关系如图1所示。

图1 数据集之间的关系

（1）嗅感评价数据集。嗅感评价是49位志愿者对有高低浓度的476种气味提供的21种给定的嗅觉感知评分，评分是0～100分，21种嗅觉感知评分的标签（简称嗅感描述符）为Intensity（强度）、Pleasantness（愉悦度）和其他19种等。考虑到个体差异性的因素，本文预处理该数据集的方法是：对没有评分的空值取0值代替，每种气味分子的嗅感评分取均值，高浓度和低浓度的评分合并一起，最后得到一个大小为476×21的嗅感评价数据集。

（2）物化特征数据集。本文使用的气味物化特征（即分子描述符）数据集来自本团队实验室的DRAGON 7软件，对比“梦想嗅觉预测挑战赛”官方通过DRAGON 6软件给定的分子描述符为4884个，而DRAGON 7涵盖了5270个分子描述符，包括组成描述符、分子性质描述符、拓扑描述符和几何描述符等。本文获取分子描述符的方法是，预先人工整理476种气味分子的CID编号，其中CID编号是国际生物学用来标识分子结构化合物的数字编号，然后把CID编号导入PubChem公开化学物质数据库种，以获取476种分子的Smile数据，最后将Smile导入DRAGON 7软件，即可获取到气味物化特征数据集，大小为476×5270。考虑到数据集维度较大，并且为了剔除过多的噪声，本文对该数据集的预处理方法是：①为了减少无效特征，故删除缺失值大于5%的列；②对剩余的缺失值用其所在列的平均值填补；③为了减少数据因量纲不同造成不良印象，故提前对数据进行标准归一化。最后得到一个大小为476×2779的物化特征数据集。

1.2 随机森林（Random Forest）

随机森林是采用分类树和回归树作为基模型的bagging集成学习方法，同时也是广泛使用的特征选择方法。大量实验结果表明，随机森林算法对存在异常值的数据和噪声数据具有很好的鲁棒性，适合处理高维数据，预测准确率很高，并能给出变量的重要度评分，其变量重要度度量能作为特征选择的一种工具，近年来已被广泛运用于分类、回归预测以及异常点检测等问题［1］。随机森林算法能计算变量重要度（variable importance），这也是作为特征选择的根本依据。假设一个数据集X的特征有m个，即X1,X2,X3,…,X i,…,X m，其中计算第i个特征的重要度评分为VI M i G in i，即第i个特征在所有决策树中节点分裂不纯度的平均改变量［2］。因此要计算变量重要度，需要使用基尼指数，它表示一个被随机选中的样本被误分的比例：

在节点m中类别k的概率是p mk。在节点m处前后的基尼指数变化量为

这里的G I l和G I r分支前后的基尼指数。若X i遇到的节点（第j棵树）为集合M，X i在该树的变量重要度评分为

假设一共有n棵树，则有

最后，对之前得到的重要度评分做归一化处理：

按照上述原理给2779个特征进行重要度排序，即可进行特征选择，这里设置一个特征重要性的阈值，大于该阈值的特征保留下来，其中阈值的大小为特征重要性的均值。随机森林的特征选择结果如表1所示。

表1 随机森林的特征选择结果

1.3 主成分分析（PCA）

主成分分析方法（PCA），是一种广泛且常用的降维算法，它是由卡尔·皮尔逊于1901年发明，用于分析数据及建立数理模型，在原理上与主轴定理相似。之后在1930年左右由哈罗德·霍特林独立发展并命名。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，简言之，新的维度是旧的维度的线性组合。主成分分析法只能识别出总体的变异，而不能区分组间和组内的变异，不能有效地利用数据中的非线性组合［3］。我们假设输入数据集X为m×n维，X=(x1,x2,x3,…,x m)，进行样本中心化，得

得到协方差矩阵：

分解协方差矩阵，从大到小进行排序得到的特征值，为λ=(λ1,λ2,…,λk)，其特征向量为w=(w1,w2,…,w k)，得到特征向量矩阵W，并将转置后的W乘以x(i)：

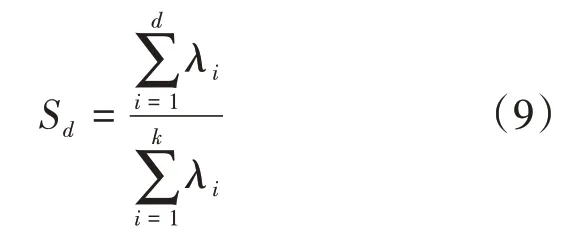
作为PCA重要评估指标，选择累计方差贡献率需要高于90%。本实验中所选取的维度为50，对应的累计方差贡献率为91.26%。

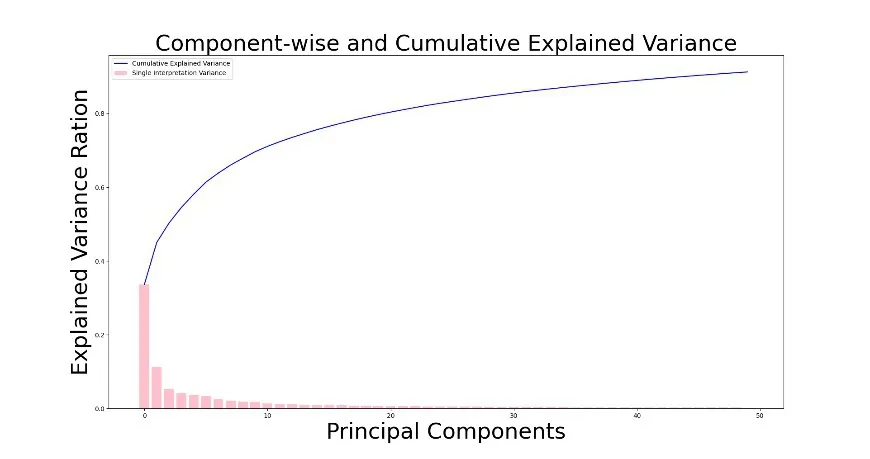
图2 PCA降维结果

2 基于Ridge Regression的嗅感评价模型

岭回归、吉洪诺夫正则化（Tikhonov Regularization）是专用于共线性数据分析的有偏估计回归方法，由Hoerl和Kennard于1970年提出的。岭回归实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法［4］。岭回归算法虽然存在一定的主观性，但针对自变量之间存在多重共线性、线性回归方差大等问题，人工去调控岭参数能较好地解决。

最小二乘法回归是一种无偏估计，而岭回归则在其基础上带了二范数惩罚。在最小二乘法中，矩阵X通常是列满秩的：

其中定义损失函数为Xθ和y两者残差的平方：

在损失函数基础上加上一个正则化项：

这里定义Γ=αI，I是单位矩阵，对上式求导得到最小化目标函数：

其中θ(α)随α变化的轨迹，称为岭迹［5］。在本文中引入相关指数R2和均方根误差RMSE来对模型拟合程度进行评估。R2的取值范围是0～1，越靠近1，拟合程度越高，反之拟合程度越低，RMSE的取值越靠近0，拟合程度越高。在本实验中，根据两种评估指标，采用5折循环交叉验证对结合3种特征空间的岭回归模型进行评估。

3 实验结果分析

在本文中，使用未经降维的物化特征数据集训练的Ridge Regression模型结果作为Baseline。其中观察到Ridge Regression模型中的参数α大于1000后，各个指标的变化甚小，故设置范围是0～1000，步长为10，经过调试确定了在每种特征空间模型下的最优参数α，如表2所示。

表2 岭回归模型α参数设定

将每个气味描述符（嗅感评价）都作为目标，输入随机森林和PCA得到的特征空间到学习器，其中训练集和测试集按照数据集的70%和30%的比例划分，修改参数调优后，在测试集上的结果如表3、表4所示（其中Random Forest简称RF），同时画出相对应的岭迹图，见图3、图4。

图3

图4

表3 RMSE评估比较

表4 R 2评估比较

将基于两种特征筛选方法的模型的预测结果与Baseline的预测结果进行对比，两种标准下的结果相差无几。以R2为标准，两种算法在对一些特定的嗅感描述符具有提升效果，基于随机森林算法的模型中有11个模型优于Baseline，基于PCA算法的模型中有6个模型优于Baseline，而在其他的嗅感评价模型上低于Baseline。

（1）首先仅取3种模型的21种嗅感描述符R2的平均值进行比较：PCA（0.159）＜Baseline（0.169）＜随机森林（0.179）。运用PCA算法进行特征提取减少特征维度数98.20%，但是在求21种嗅感描述符的综合性能效果较差；运用随机森林算法进行特征选择将平均提升模型性能5.78%，平均减少特征维度数88.38%。

（2）在Baseline的基础上，将随机森林算法优选出的11个模型和PCA算法优选出的6个模型，取代Baseline上原有的模型，得出的R2的平均值比较为：Baseline（0.169）＜改进PCA（0.170）＜改进随机森林（0.227）。可以看到改进后的PCA算法模型综合性能有所提升，而改进后的随机森林算法的模型性能提升明显，平均提升模型性能33.04%。

4 结语

本文主要是通过两种不同的特征筛选方法挖掘数据集更深层的关系，形成较为合适的特征空间，利用不同方法得到气味的物化特征空间作为输入，嗅感评价作为输出，使用机器学习方法构建从气味的物化特征空间到嗅感评价的映射模型。由实验结果可知，基于特征选择的Ridge Regression模型比基于特征提取的Ridge Regression模型预测效果更好，为对气味物质嗅感的自动评定做出了一定的贡献，为构建更好的嗅感评价模型奠定基础。