基于汽车价值链业务协同资源的配件销量预测模型

孙磊，任春华，高雪芹，王波

（1.西南交通大学，制造业产业链协同与信息化支撑技术四川省重点实验室，成都 611756；2.北京机械工业自动化研究所有限公司，北京 100120；3.成都国龙信息工程有限责任公司，成都 610036）

0 引言

随着中国汽车工业的迅速发展，汽车销售市场需求日趋饱和，市场竞争更加激烈。尽管在2020年新冠疫情的影响下，人们的消费需求有所降低，全球汽车产业链受到了巨大冲击，但我国克服重重困难，其中汽车行业率先恢复生产。据公开资料显示，2020年中国汽车销量为2531.1万辆，同比仅下降1.9%，降幅比上年大幅收窄了6.3%［1］。为了提高市场占有率，配件代理商必须向客户提供优质的服务。这就要求代理商要有足够的库存以满足及时发货的需求，然而为了减少库存成本，代理商又必须适当降低库存。为了缓和这两者之间的矛盾，通过汽车配件市场销量预测，建立合理库存管控机制显得尤为重要。本文依托汽车价值链业务协同平台［2］，面向产业链上的配件代理商，整理配件销售业务数据，分析该企业在一段时间内的销售情况，提出了一种BPGRU组合模型进行配件销量预测，为配件代理商下一阶段的配件进货与库存管控提供决策支持。

1 相关工作

随着人工智能、机器学习等领域的高速发展，BP、GRU、ARIMA、LSTM等网络模型广泛应用于预测场景中，取得了一些丰硕的成果。冯晨等［3］提出了一种ARIMA、XGBoost和LSTM进行加权组合的预测模型，以提高多变量商品销售的预测精度。邓青等［4］在研究微博转发行为时，采用BP神经网络对突发事件的转发量进行预测，获得了极具参考意义的实验结果。为更好地预测产品销量短期及长期的变化趋势，葛娜等［5］将Prophet与LSTM进行结合提出了一种新型组合预测模型。李祚敏等［6］引入鲸鱼优化算法，提出了一个优化网络权重的GRU神经网络用于预测防晒用品的销售情况。Wang等［7］收集了从2008年起至2017年台湾出口经济的关键指标数据，并通过相关分析选择重要的变量，采用人工神经网络对注塑机的销售情况进行预测。

针对汽车零配件销售及需求情况的预测，在近年来也成为一项热点研究。荆园园等［8］通过研究影响汽车零配件需求量的各种因素，提出了一种基于BP神经网络的预测模型。吕鹏飞等［9］构建了一个基于回声状态网络的配件库存预测模型，并将其应用于汽车配件的需求预测问题。Gong等［10］将季节变化指数引入到GM（1,1）中，以提高模型在预测非线性汽车零部件销售情况时的准确性。方瑜等［11］对二手汽车售后配件销售规律进行了分析，并提出了一个可有效解决二手汽车配件预测问题的ARIMA模型。此外，方瑜等［12］还提出了一种结合ARIMA与BP神经网络的组合模型对二手汽车配件需求进行预测，进一步通过真实数据集证实了该模型的有效性。

2 组合预测相关模型构建

2.1 模型相关理论

本节主要介绍BP神经网络和GRU网络模型，分别从其内部结构和核心原理进行阐述，方便进行两个模型的有效组合。

2.1.1 BP神经网络

BP神经网络是由Rumelhart等［13］提出的，它是一种误差逆传播的多层前馈网络。通过反向传播的方式来调优网络的权值和阈值，使得其误差平方和最小。BP神经网络的拓扑结构包括输入层（Input Layer）、隐藏层（Hide Layer）和输出层（Output Layer）。其网络拓扑结构如图1所示。

图1 BP神经网络拓扑结构

BP算法的核心为信息的正向传播与误差的反向传播［14］。

（1）信息的正向传播。在信息的正向传播过程中，数据经由输入层进入，经过隐藏层的处理之后再次进入输出层。当输出层的输出结果与期望的输出结果不同时，便会进入误差的反向传播过程［15］。

BP神经网络的输入层与隐藏层节点之间以权重连接。正向传播时，隐藏层的第一个神经元从输入层的每一个神经元处得到输出值，加权求和，阈值，激发函数f1，得到该神经元的输出值如公式（1）所示：

输出层第一个神经元a1得到隐藏层每一个神经元输出值，加权求和，阈值，激发函数f2，得到该神经元的输出值如公式（2）所示：

（2）误差的反向传播。向输入层输入n个I维数据样本，正向经隐藏层处理后，传入输出层，得到实际输出a。在输出层把实际输出a和期望输出t进行比较，计算均方误差如公式（3）所示：

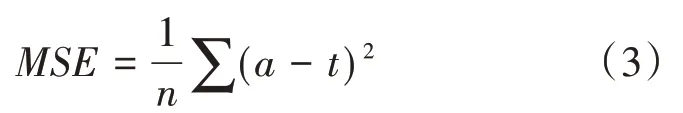
若M S E没有达到预设的误差精度ε，算法进入误差的反向传播过程。M SE以梯度形式按原来正向传播的通路逐层反向传回。同时，反向传回的MSE被分摊给各层所有神经元以获得各层神经元的误差信号M SE j（j=1，2，3）。MSE j作为修正各连接权值和阈值的依据，对其进行修改。

BP算法反复运行信息的正向传播和误差的反向传播两个过程，直至误差信号MSE收敛于预设的精度ε或达到预设的最大训练次数［16］。

2.1.2 GRU网络模型

LSTM模型广泛应用于时间序列数据的预测，但由于其内部结构复杂，导致LSTM模型在进行数据训练时需要花费很长时间，所以出现了许多LSTM变体。Cho［17］于2014年提出了GRU网络模型。GRU通过将遗忘门和输入门结合在一起形成了更新门（Update Gate），并且将细胞状态和隐藏层状态合并在一起，使得模型结构比LSMT模型更加简单。GRU内部结构如图2所示。

图2 GRU内部结构

GRU的计算公式如式（4）—式（7）所示。

其中W r、W z和W表示需要训练的权重矩阵。当R t越接近于0，则表明前一时刻贡献的有效信息越少，而Z t越小，则表明前一时刻贡献的有效信息越多。

2.2 组合模型构建

BP网络是目前应用最多的一种神经网络，它具备神经网络的普遍优点，能够有效处理回归问题，但对长时序列数据的感知能力有所欠缺。而GRU能够有效地处理长时预测问题，且结构相比LSTM更简单。因此，本文将基于BP和GRU网络构建一种BP-GRU组合预测模型，用于汽车零配件销售预测。BP-GRU模型的结构如图3所示。

由图3可知，BP-GRU模型首先利用BP网络对数据的特征进行初步提取，接着利用GRU捕获时间长期依赖性，最后将BP和GRU的预测结果进行加权融合，得到最终的预测结果。

图3 BP-GRU模型结构

3 实验分析

3.1 实验环境及数据

本文实验环境如表1所示。

表1 实验环境

为验证BP-GRU预测模型的准确性与高效性，本实验采用3种数据集，分别是PRSA_Data_Wanshouxigong_20130301-20170228数据集（以下简称PRSA_Data_A）、PRSA_Data_2020.1.1-2014.12.31数据集（以下简称为PRSA_Data_B），和汽车价值链业务协同平台上的某代理商平台的2018—2020年的某配件的销售数据。其中配件销售数据的特征维度选择整车保有量、使用时长、配件故障率。3种数据集分别对模型进行训练与测试。

为避免原始数据在模型预测过程中由于数据不规范、缺失值和脏数据等对结果产生影响，首先要对采集的数据进行预处理。

（1）数据填充。在数据采集或者是记录过程中出现了样本数据为空或者是缺失的情况，采用数据填充的办法，采用缺失位置前后数据的平均值来填充。

（2）数据归一化处理。由于数据上下界存在较大波动，因此将数据进行归一化处理如公式（8）所示，减少数据本身对预测结果的影响。

其中xnorm表示归一化后的值，x i为归一化前的值，xmin为最小的样本值，xmax为最大的样本值。

3.2 实验方案及参数选择

本文提出的组合预测模型采用M S E作为损失函数，使用Ad am作为优化参数。实验中选用RMSE和M AE作为评测指标，以评估模型预测精度，两个评价指标值越小，表明模型的性能越优。相关参数的取值情况如表2所示。评价指标计算如式（9）、式（10）所示。

表2 参数取值

其中n表示样本数量，y i表示数据的值，表示预测值。

3.3 实验结果分析

本文选取BP模型、GRU模型、CNN模型、LSTM模型和RNN模型作为对比实验模型，与本文提出的BP-GRU模型进行性能对比，通过RMSE与MAE值进行比较。

PRSA_Data_A数据集的实验结果如表3所示。BP-GRU模型的RMSE和MAE取值分别为24.87和12.35，均低于其他5个对比模型，说明本文提出的模型预测精度更高。

表3 PRSA_Data_A数据集实验结果

PRSA_Data_B数据集的实验结果如表4所示，在RMSE的比较中，LSTM的评价函数值是23.73排名第一，而我们的BP-GRU模型排名第二，但均比单独的BP与GRU模型的效果更好。在M A E的比较中，BP-GRU取值是12.81，排名第一，而LSTM的M AE值是12.82。BP-GRU与LSTM模型性能相近，但BP-GRU优于BP、GRU、CNN和RNN。

表4 PRSA_data_B数据集实验结果

配件销售数据集的实验结果如表5所示，在R M S E的比较中，BP-GRU模型取值最低。在M A E上，LSTM的取值最低，BP-GRU模型排第二，但均比单独的BP与GRU模型的效果更好。说明BP-GRU模型优于BP、GRU、CNN、和RNN。

表5 配件销售数据的实验结果

4 结语

本文以配件代理商的配件销售数据为研究对象，提出了一种BP-GRU组合预测模型，用于预测配件的销售情况，与此同时采用其他数据集与模型进行对比实验。实验结果表明，该组合模型在3种数据集上的预测效果比起其他单一的模型效果更好。该模型可应用于汽车价值链中售后服务时配件销售预测情况，对代理商下一阶段的采购提供决策支持。本文目前探索了BP-GRU模型的组合情况，下一步的工作可在此模型的基础上进一步组合或是对该组合模型进行参数调优，以提高预测精度。