高速列车模糊RBF神经网络速度跟踪控制

莫晓婷，王雪奇，梁新荣，董超俊

（五邑大学智能制造学部交通工程系，江门 529020）

0 引言

在人工智能的推动下，各国专家学者开始对基于智能控制方法的列车速度跟踪控制产生了浓厚的研究兴趣。对动车组来说，如果要对其速度进行跟踪控制，就要有合适的高速列车动力学模型作为基础。综观现有的文献，高速列车动力学建模根据是否将一辆列车看作一个整体可以分为单质点建模和多质点建模。蔡鹏翔等人利用单质点列车模型建立了相应的随机离散方程，然后运用两种辨识算法验证其有效性［1］。何之煜等人将高速列车看作一个质点，采用自适应模糊滑模算法消除原有速度跟踪曲线的振荡现象，对列车速度进行控制［2］。杨罡等人提出一种在非线性模型基础上的预测控制，通过微分方程建立单质点列车模型，提高了列车速度控制的精度［3］。单质点模型应用很多，建模过程简单，但其存在着忽略车间内力故而计算精度不高的缺点。贾超等人建立了多质点模型，利用非线性的预测控制实现了对动车组轨迹的追踪［4］。HOU T等人将每个车厢看作一个质点对象，利用模糊自适应PID控制器来跟踪列车的速度［5］。王龙生对一辆列车的动态特性用非线性方程进行描述，将列车的运行状态作为参考变量建立了混杂的多质点列车模型［6］。多质点模型虽然考虑了车厢之间的相互作用力，但其存在计算过程复杂不利于列车在线控制运行的缺点。综上，本文建立了单位移多质点模型。

再者，列车速度控制方法的研究也开始变得多种多样。GUO X等人研究了动车组在输入过大时的动态追踪问题，研制了CNN与滑模控制相结合的列车速度控制器，实现了对列车目标速度曲线的跟踪处理［7］。侯涛等人采用预测模糊控制器并用多点模型控制列车的速度，使列车以期望的速度运行，满足快速响应和高控制精度的要求［8］。孟建军等人利用多个控制方法对列车的速度-距离目标曲线进行跟踪控制与仿真比较［9］。FU P等人采用PID控制对高速列车速度进行控制，并提出了基于速度跟踪误差和速率驱动的事件触发反馈控制方法［10］。李中奇等人采用双自适应广义预测控制方法使列车速度跟踪的精度更高、性能更稳定［11］。刘开伟基于遗传算法提出了一种全新的文化基因算法建立了列车模型，运用动态矩阵控制设计列车速度跟踪控制器，使得列车实际速度可以完美地跟踪期望速度曲线［12］。上述列车速度控制研究已经包含了一些通用的控制算法，例如，滑模控制、预测控制等，这说明智能控制是列车速度控制的一个研究热点，人工智能是未来发展的方向。

本文建立一种单位移多质点的高速列车动态模型，并设计一种基于模糊RBF神经网络的高速列车速度跟踪控制，最后提供数值仿真来证明所提出方案的有效性。

1 高速列车动态模型

如图1所示是一辆由n节车厢通过耦合器相连接的高速列车示意图。

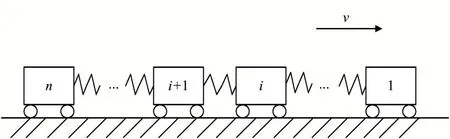
图1 n节车厢连接的列车示意图

设xi为第i节车厢的位移，xi-1为第i-1节车厢的位移，Δxi-1表示第i节车厢和第i-1节车厢之间的距离，则它们之间的关系可表示为：

根据式（1），可以得出相邻两车厢之间的位移、速度和加速度的关系式为：

式中，˙和分别表示第i节车厢的速度和加速度，和分别表示第i-1节车厢的速度和加速度，和分别表示第i节车厢和第i-1节车厢之间的相对速度和相对加速度。

选择第1节车厢作为参考点，则第1节车厢和第i节车厢之间的位移、速度和加速度可描述为：

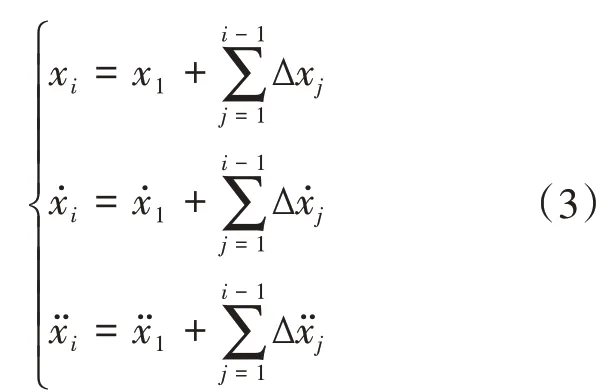
式中，x1、和分别表示首节车厢的位移、速度和加速度。

选取上述列车第i节车厢作为一个质点进行受力分析，如图2所示，可知该车厢受到牵引力和制动力、车厢与车厢之间的作用力以及运行阻力的影响，其中运行阻力包含了基本阻力和附加阻力。

图2 一个车厢的受力分析

图2中，ui表示第i节车厢的牵引力和制动力；fr i表示第i节车厢的附加阻力，由于运行线路的不同，附加阻力可以是弯道阻力、坡道阻力以及隧道阻力等；fhi表示第i节车厢的基本阻力，其表达式为

f hi=a+b v+cv2，其中a、b和c是基本阻力参数；fi-1表示该车厢受到的前节车厢的作用力，fi表示该车厢受到的后节车厢的作用力，第i节车厢与前后相邻车厢之间的作用力fci可表示为：

然后，根据牛顿第二定律有:

式中，mi表示第i节车厢的质量。

将式（4）中车厢之间的作用力关系代入到式（5）中可以得到：

将式（3）中的加速度关系式代入到式（6）中得：

因为第一节车厢只受到了第二节车厢给的作用力，故f0=0，最后一节车厢只受到了前面一节车厢给的作用力，故f n=0，将其代入式（7）并将式（7）两边相加，会发现车间力fi都相互抵消了，但相邻车厢间存在由于车厢之间相对加速度引起的车间作用力，于是便得到单位移多质点列车模型，即：

式中，等式左边只存在首节车厢的加速度x¨1，x¨1对应首节车厢的位移x1，因此该模型称为单位移多质点列车模型，它不仅考虑了车厢之间的相互作用力，而且还解决了以往多质点模型计算量过大的问题，因此，能更好地描述列车的动态特性。

2 高速列车模糊RBF神经网络PID速度跟踪控制

2.1 模糊RBF神经网络

图3是FRNN结构图，各层含义解释如下：

图3 FRNN结构

第一层：每个神经元节点都与对应的输入变量连接，从而将输入传递给下一层，故节点i的表达式为：

式中，xi是输入；f1（i）是该层的输出。

第二层：其输出为：

式中，f2（i,j）为模糊化层的输出；cij表示该层激活函数的中心；b ij表示该层激活函数的宽度。

第三层：将第二层输出的信息作为这一层的输入量，传到该层各个神经元节点。该层输出为：

式中，f3（j）是输出；n表示输入层输入量的个数。

第四层：将第三层的输出进行加权组合，即：

其中，l是节点数，因为输出层的输出对应PID的三个参数，因此，l=1，2，3，且f4（1）、f4（2）和f4（3）分别对应kp、ki和kd，w（l，j）即wl j，表示第三层节点j与第四层节点l相连接的权值；N表示模糊推理层的节点数。

2.2 模糊RBF神经网络PID控制

图4是FRNN PID控制图，它将期望输出与实际输出的差值e和差值变化量作为神经网络的输入量，而其输出为PID的三个参数，然后通过整定后的PID求出控制变量u。

图4 FRNN PID控制

首先，根据式（12）可以得到上述FRNN PID控制器的输出增量，即：

式中，Δu（k）表示k时刻系统的控制输出增量，kp、ki、kd和xc（1）、xc（2）、xc（3）由式（14）和式（15）确定：

式中，e（k）是k时刻的误差。

则有：

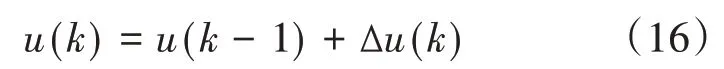
式中，u（k）表示k时刻系统的控制输出，u（k-1）表示k-1时刻系统的控制输出。

接着，选择有监督的Delta学习规则来调整参数，令目标函数为：

式中，yd（k）表示系统的期望输出，y（k）表示系统的实际输出，且e（k）=yd（k）-y（k）。

则FRNN PID控制器的权值修正学习算法为：

式中，η是学习速率，α是学习因子，且0＜η＜1,0＜α＜1。

2.3 基于模糊RBF神经网络PID的高速列车速度跟踪控制器

高速列车的运行环境十分复杂，为了确保在不同线路上任意给定列车一期望速度，列车都可以在允许误差范围内跟踪它且安全运行，需要设计与之对应的速度跟踪控制器。如图5所示的控制器是本章设计的速度控制器，这里采用第1节建立的单位移多质点列车模型，该模型考虑了基本阻力、附加阻力和车厢之间的作用力，系统的输入是列车期望速度vd，这里对应图4中的yd，系统的输出是列车实际速度va，这里对应图4中的y，系统的误差信号error是列车期望速度与实际速度之差，这里对应图4的e，单位牵引力和制动力是控制变量u，通过选择合适的牵引力和制动力使列车实际速度跟踪列车期望速度。

图5 FRNN PID速度跟踪控制器

下面介绍具体的学习算法步骤：

（1）输入高速列车的期望速度vd，根据列车型号和运行线路设置基本参数和运行参数；

（2）设置FRNN的四层节点数，将kp、k i、kd三个参数作为FRNN的输出，设置bij、cij和wlj的初值；

（3）选取学习速率η，学习因子α，将列车期望速度vd（k）与实际速度va（k）的差值作为系统的误差信号，即error（k）=vd（k）-va（k）；

（4）根据式（9）至式（12）计算出FRNN每一层的输出值，再通过式（13）至式（16）计算系统的控制量u（k），也就是列车的单位牵引力和制动力；

（5）由式（17）至式（19）通过更新神经网络的权值来调整PID控制器的三个参数，产生新的控制量u（k），就有新的牵引力和制动力作用于列车上，从而使列车获得新的实际速度，即完成一次速度跟踪过程。

图5是一个非线性反馈闭环控制系统，与开环控制相比较，这种非线性反馈可使系统具有好的稳定性和强的抑制干扰的能力。

3 仿真实验与结果分析

采用CRH380动车组列车的基本参数，即，该列车由四节拖车和四节动车组成，列车重量为840 t，基本阻力公式为a+b v+cv2，其中参数a、b、c的选取数值分别为0.53、0.0039、0.000114，且列车的牵引和制动特性如表1所示。

表1 列车的牵引和制动特性

对图5所示的列车速度跟踪控制器进行仿真实验验证，采用京沈客运专线辽宁段的实际运行线路，即从阜新站到新民北站，作为仿真运行线路，列车的最高运行速度为350 km/h，自动防护限速是360 km/h，该数据来源于中国铁道科学研究院［13］。在一台配置为CORE i7内存配置为8 GB的电脑上进行Matlab仿真调试，仿真过程中FRNN学习算法的参数设定情况为：设置FRNN的四层节点数分别为2、5、5、3，选取学习速率η=0.2，学习因子α=0.02。在这台电脑上1 320个期望速度样本点的仿真时间为0.11 s，可见仿真时间极短，该算法可以应用于列车速度跟踪控制系统中去。得到图6—图9的效果图分别为速度跟踪曲线、距离跟踪曲线、速度跟踪误差曲线和距离跟踪误差曲线。

图6 速度跟踪

从图6和图7可以看出，虚线的实际速度曲线与实线的期望速度曲线几乎完全重合，虚线的实际距离曲线与实线的期望距离曲线几乎完全重合，该仿真算法实现了实际速度-时间曲线对期望速度-时间曲线地跟踪控制，同样也实现了实际距离-时间曲线对期望距离-时间曲线地跟踪控制，且追踪效果良好。由图8和图9可知，速度跟踪平均误差为0.1833 km/h，速度跟踪误差控制在-3.6148～4.0263 km/h的范围内，距离跟踪平均误差为0.7805 m。

图7 距离跟踪

图8 速度跟踪误差

图9 距离跟踪误差

为了说明本文提出的FRNN PID控制的性能，我们仍然选取CRH380型动车组参数以及第1节建立的单位移多质点高速列车动态模型，并采用相同的期望速度-时间曲线，分别用90条规则的模糊控制和单纯的PID控制编写应用程序来进行速度跟踪控制实验。实验表明三种方法都能实现对列车速度和距离的跟踪控制，但是控制效果大有不同，单纯的PID整体控制跟踪性能较差，90条规则的模糊控制的速度跟踪性能虽然较好，但其距离跟踪效果很差，且仿真时间很长，相比之下，FRNN PID控制的跟踪效果最好。表2比较了三种方法的控制性能。

表2 三种方法的性能比较

为了进一步说明本文设计的高速列车速度跟踪控制器具有良好的跟踪性能和抗噪声性能，下面对该控制器增加随机噪声干扰并进行仿真验证。仿真效果图如图10—图12所示，这三个图分别表示加上随机噪声干扰时的速度跟踪曲线、加上随机噪声干扰时的速度跟踪误差曲线和加上随机噪声干扰时的距离跟踪误差曲线。

图10 随机噪声干扰时的速度跟踪

图11 随机噪声干扰时的速度跟踪误差

图12 随机噪声干扰时的距离跟踪误差

从图10—图12中可以看到，在加上随机噪声干扰后，该高速列车速度跟踪控制器仍然有很好的跟踪性能，速度跟踪误差保持在-3.6946～3.7741 km/h的范围之内，这说明了本文设计的控制器具有很好的抗噪声干扰的能力。

4 结语

本文建立了高速列车单位移多质点模型，并利用模糊RBF神经网络PID控制设计了非线性反馈闭环控制器对高速列车速度实施跟踪控制。相对于单质点模型，多质点模型提高了建模精度。同时模糊神经网络PID控制使系统的学习速度变快、自适应能力增强，这也提高了系统的实用性，且非线性反馈闭环控制的加入使系统的控制性能进一步提高。在实际列车参数和国内高速铁路线路上真实运行数据的基础上，通过仿真验证了本文的算法在很大程度上减少了速度跟踪误差和距离跟踪误差且具有好的抗噪声能力，该算法极大地提高了速度跟踪精度，对提高列车运行效率和保证乘客的舒适度具有重要的意义。