主观题客观化的思考与实践——以《微积分学》课程为例

韩淑霞， 吴 洁， 黄永忠

(华中科技大学 数学与统计学院，武汉430074)

1 引 言

传统的高等数学课程测试中，一般有两种题型，一种是客观题，包括单项选择题、多项选择题和判断题等，另一种是主观题，包括计算题、应用题、证明题等.客观题在在线测试平台上可以直接使用，测试结果能够即时反馈给学生和老师，方便学生对自己学习中的问题进行反思、方便教师对学生的学习状况进行评判和答疑解析，促进课程的在线学习.但是主观题却不方便应用于在线平台测试.在2017年高等教育出版社组织的高等数学评测系统的在线题库启动会上，国防科技大学的朱键民教授提出了主观题客观化的思想.主观题客观化就是将主观题设计成客观题的形式，让主观题也能像客观题一样进行在线测试.

斯金纳的新行为主义理论[1]认为及时反馈是强化学习的关键，所以主观题能否客观化，怎样客观化，能否让主观题像客观题一样在在线平台上进行测试是值得探索和实践的问题.

关于测试题的设计相关文献包含两类，一类是怎么利用各类软件技术实现在线测试如文献[2-4]，另一类从教学角度对某种客观题型的设计给出了原则性建议如[5-7]，其中邹增家[7]给出了高等数学的单项选择题的设计规则和设计方法.

作者[8-9]从2016年开始在微助教平台进行了微积分大班的翻转混合式课堂实践，由于课堂教学在线测试的需要，做了主观题客观化的大量实践.本文下面将给出主观题客观化的原则，并以《微积分学》课程为例给出在线测试题主观题客观化的四种思想方法及教学案例.

2 主观题客观化规则

主观题客观化过程中应该遵循以下规则：

(i) 题目的正确性与科学上的可解性；

(ii) 以教学目标为目标. 确保通过对主观题客观化后的测试题作答，能够帮助学生理解相关知识，培养学生分析问题解决问题的能力，激发学生对相关知识点的兴趣，增进学生进一步研究性学习的可能；

(iii) 搭建起课程基础内容与课堂重难点的桥梁.主观题基本上课堂教学的重难点内容，客观化过程就是将重难点内容与相关知识点的基础内容衔接起来，测试过程就是将基础内容深化到重难点内容的思维成长过程；

(iv) 符合程序教学法原则.比如斯金纳[10]提出的小步子原则、积极反应原则、即时强化原则、自定步调原则、低错误率原则.

3 主观题客观化的四种思想方法

3.1 顶层逆向设计方法

顶层逆向设计法的具体做法：

(i) 将重难点问题利用数学分析和逻辑思维方法将其解答过程一层一层向下分解，一直分解到和学生预习的基本内容正好接轨为止；

(ii) 从基本内容或基本题目出发，以小步走的科学学习方法，一层一层逆势向上，设计出体现基本解题过程中的每一小步和及其拓展的基础命题，这样就可以得到一组正确的基础命题；

(iii) 根据往届学生常犯的错误，对上述正确的基础命题进行错误分析法，相应得到一组错误的基础命题. 这样从一道重难点题目出发，就设计出一个重难点题目的正确命题模块和错误命题模块，设计方案如图1；

图1 重难点题目的顶层逆向设计法

(iv) 从这两个模块中任意抽取一个命题就可做为判断题，抽出3-5个命题进行有机组合就可设计出多个多项选择题或者单项选择题，而这种组合功能可以利用一些学习软件辅助实现，这些选择题就形成了重难点题目对应的复合测试题模块. 具体班级的课堂上根据学生的具体情况从目标题目模块中进行选择使用.

比如《微积分学》课程在极限四则运算和复合运算部分，有一道这样的重难点题目：

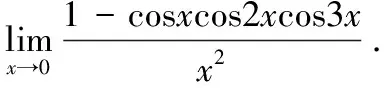
图2 重难点题目的析错设计方法

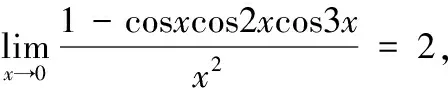
将上面(i)～(vii)进行组合，可以设计多个复合型测试题，比如结合(v)和(vii)，可以设计下面的单项选择题：

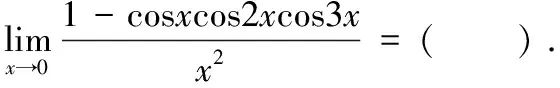
(A) 1/2 (B) 2 (C) 9/2 (D) 7

结合(ii)，(iii)，(vi)，(vii)设计下面的多项选择题：

题目内容：下面选项正确的是( ).

3.2 析错设计法

对于某一个知识点，依据平时学生作业中所犯的各种错误析取出来，用每一种错误的解法就会得到错误命题，这就是析错设计法，如图2. 将错误命题作为选择题的干扰项，可以设计出更多的单项选择题或者多项选择题. 析错法设计法的好处在于精准击中学生所犯错误，教师只需要画龙点睛做一些解释就会做到药到病除，比起传统课堂上教师费破了口舌讲解的效果要好.

比如在第二型曲线积分这部分内容的计算题目，在掌握了二重积分的基础上学生计算常犯的有两种类型的方向错误：

错误1：忽略二型曲线积分的积分曲线的方向；

错误2：使用格林公式时忽视封闭曲线的正向(逆时针方向为正)条件.

针对上面两种错误类型，相应的题目可以设计出三种的错误解法，第一种犯错误1，第二种犯错误2，第三种犯错误1和错误2. 正确解法答案唯一. 这四种解答的答案作为选择支得到的单项选择题. 作者采用这种析错设计法在微助教平台上在测试了一道第二型曲线积分的题目，并将测试题目的内容以及两个微积分大课堂的学生答题情况截屏如图3所示.

图3 第二型曲线积分的一道选择题及学生答题情况

(A) -4π+e2-1 (B) 4π+e2-1

(C) 4π-e2+1 (D) -4π-e2+1

微助教平台在测试完成后，立刻将学生答题情况显示如图3的直方图，完全区分了学生所犯三种错误的情况. 忽视了格林公式的封闭曲线方向的答案为(A)选项，弄错了曲线积分中曲线的方向的答案为选项(C)，两个方向都错误的对应答案是选项(D)，选项(B)是正确答案，错误率占到了约1/3，正确率约2/3. 每个答错学生根据在线测试平台的反馈就明白了自己所犯错误，达到了最初设计此测试题的教学目的.

3.3 强化书写步骤方法

在《微积分学》的课程教学中，不管是学生的作业还是学生的考试卷，经常会发现学生解答过程出现逻辑混乱的问题. 其实一个题目的解答书写过程恰好体现了答题者的思维逻辑是否严密有序，数学分析是否正确清楚，而且好的数学表达也会为学生后期进行专业课的学习和科学研究打下良好的基础，所以在数学课程教学过程中，无论怎么强调书写过程的正确性也不过分. 其次书写过程的步骤恰巧体现了教学中需要强调的教学内容，也可将每个步骤所对应的小知识点分离出来单独强化，所以可将同类型重难点题目的同一步骤剥离出来点单独考察，有助于整体上更好地掌握这个知识点. 在分解重难点题目的解答步骤时仍然需要强调小步子原则，不怕步骤多，一定要分解到和学生学过的基本公式、定理或者方法技巧相联通，让学生在解答强调书写步骤法的测试题时能体会出数学思维的逻辑过程和数学分析的方法，达到培养学生形成正确逻辑思维和严谨数学表达的效果. 强化书写步骤法的测试题设计方法如图4.

图4 重难点题目的强化书写步骤设计方法

这里以球面坐标系下三重积分的计算题目入手来探讨这部分题目的设计.

从例2的解答可分为四个步骤：重积分的对称性质，怎么利用对称性将积分转化为适合球面坐标系下的积分；怎样将三重积分转化为球面坐标系下的三次积分，如何计算三次积分. 在解决球面坐标系下的三重积分计算之前，先让学生逐一掌握四个基本的知识点，然后再来强调三重积分的步骤书写. 只需要将四个步骤按顺序组成一个阅读题，或者将学生常犯的错误加入某一步骤，然后按顺序(不能用梅花序)得到一个选择题，最好设计成多选题. 在微助教上，作者曾将最后一步的计算结果改成错误结论得到一个多选题，现将微助教上的测试题以及两个大班学生的测试结果截屏如图5.

图5 球面坐标积分的一个计算题及解答情况

从图5中的微助教反馈的直方图可以看出，学生经过前期基本知识点的训练，对此类题目的解答过程已经熟悉，但其中一个班对于球面坐标系下重积分化为累次积分还有所欠缺，所以这个班就需要在球面坐标系下重积分化为累次积分方面多加练习，另一个班只需对个别同学提出建议即可.

3.4 一题多解设计法

在培养学生数学分析和多角度逻辑思维能力方面，一题多解有无可挑剔的优越性. 一题多解通常在方法总结、以及不同方法之间的关联等起到不可替代的作用. 但一题多解应该是主观题客观化中最难的一种情形，计算题有一题多解，证明题也有一题多解，怎么针对一题多解设计客观题呢？首先将题目的各种解法(包括错误解法)依次整理出来不同的思路以及不同的结论，从思路和结论中挑选出3～5种为选择支即可得到选择题. 此时每个选择支尽可能体现不同的解题思路，这样得到的选择题不一定有完整的解题或证明过程，但充分体现了一题多解的解题思路. 一题多解设计法归纳为图6.

图6 一题多解测试题设计方法

下面给出一道证明题和一道计算题的一题多解的客观题设计方法.

例3设f(x)在[a,b]上连续，在(a,b)内可导(a>0)，试证在(a,b)内至少存在一点ξ满足2ξ[f(b)-f(a)]=(b2-a2)f′(ξ). 则下面证明思路正确的是( ) .

(A) 做辅助函数F(x)=f(x),G(x)=x2,利用柯西中值定理可得结论

(B) 构造F(x)=x2[f(b)-f(a)]-(b2-a2)f(x),可由罗尔定理证明结论

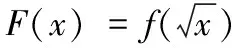
这道题的正确答案为(A)、(B)、(D)，而(C)是一种错误解答. 这里三种正确解法(A)、(B)、(D)分别给出了用柯西中值定理、罗尔定理及拉格朗日定理证明同一道题的思路，从而反映出三个中值定理在一定条件下是等价的，而(C)这个错误选项也体现了学生对微分中值定理中的中值理解不到位常犯的一种错误. 所以这道证明题的客观化设计充分体现了微分中值定理的总结和其相互关联，也是一种思考和总结.

例4求xy′=x-y的通解.

此题可用三种不同思路，一种是化为一阶线性非齐次方程，另外两种是分别以x，y为自变量可分离变量的方程求解，这三种解题思路和正确答案作为四个选择支就设计了如下一道多项选择题.

题目内容 对于方程xy′=x-y,下列说法正确的是( ).

4 结 论

主观题客观化问题是很多课程，尤其是理工类课程开展混合式教学中一个棘手的问题. 如果解决了主观题客观化问题，就等于消灭了这些课程开展混合式教学的拦路虎. 本文以《微积分学》课程为例创造性地提出了四种主观题客观化方法，并进行了举例说明，这些思路和方法同样适用于其它理工类课程. 如果主观题客观化问题解决好了，理工类课程的课程考试就可以加大客观题所占的比例，甚至完全采用客观题线上考试，这样也可以减少主观题在人为批改时所产生的误差，也减轻了教师批改试卷的工作量. 主观题客观化主要是用于线上线下的混合式教学中，这些思想方法对这方面的教学改革一定也会起到不可估量的重要作用. 同时会提升高校教师的教学技能和教学研究，进一步促进学生的自主学习、逻辑思维、数学分析等方面的能力.

主观题客观化方面，目前还有一些不足之处，还需要大量的客观实践和实验研究去比较此方法与传统课堂讲授方法谁更有效，还需进一步给出主观题客观化方法是否能够在在线平台上完全取代或者部分取代传统课堂的重难点讲授的结论.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.