线性代数课程思政教学案例的设计与实践
2021-10-30陈建龙
何 薇, 陈建龙
(东南大学 数学学院,南京211189)
1 引 言
线性代数是高等学校理、工、经、管、医、文等多个学科学生必修的公共基础课,在学生的知识构筑中发挥着极其重要的奠基作用.如何在受众面如此广泛的基础课程中融入思政元素,使学生在打牢基础知识的同时,提高思想修养、树立家国情怀是一个值得深入研究和探讨的问题.
习近平总书记在全国高校思想政治工作会议讲话中指出:“要用好课堂教学这个主渠道,思想政治理论课要坚持在改进中加强,提升思想政治教育亲和力和针对性,满足学生成长发展需求和期待,其他各门课都要守好一段渠、种好责任田,使各类课程与思想政治理论课同向同行,形成协同效应,推动‘思政课程’向‘课程思政’的立体化育人转型,实现全程育人、全员育人、全方位育人.” 习近平总书记的重要论述是课程思政建设的科学指南,赋予课程思政建设理论认知、方法认知和精髓要义,给我们指明了前进的方向.
在习近平总书记关于课程思政总的指导方针下,全国高校各门类课程的思政建设正如火如荼的进行.就线性代数课程思政建设而言,在课程思政教学体系建设[1]、教学案例设计[2-3]、教师素质培养[4]等方面都积累了一些有益经验.经过前期的建设和发展,课程思政建设已进入高质量发展阶段,需要总结前期建设中的经验和不足,并加以改进和提高.例如在教学案例的设计方面,仍存在思政教育与专业教育“两张皮”的现象,思政内容的加入给人以牵强附会,生搬硬套之感;另一方面,课程思政教学案例的数量和质量均需要进一步充实和提高.本文作者在借鉴兄弟院校已有经验的基础之上,结合作者以及东南大学线性代数教学团队的教学实践[5-6],谈谈如何将课程思政内容有机的融入到线性代数教学案例的设计之中.
2 线性代数课程思政教学案例的设计
线性代数课程思政教学案例设计的总体原则在于以课程内容[7]为源头,综合运用三个课堂,即学习的课堂、文化的课堂、实践的课堂,多方面、多层次地将思政内容融入到课程当中,培养学生的数学思维与科学素养,帮助学生树立文化自信与激发爱国情怀,引导学生学以致用,报效祖国,从而达到“立德树人”的根本目的.基于上述原则,我们把线性代数课程思政的教学案例设计分成以下三类来分别阐述.
2.1 “思想引领”类——体现在“学习的课堂”
线性代数课程的诸多内容蕴含了深刻的数学思想方法,也是马克思主义哲学思想的具体体现[8].例如n维空间的构建过程,是从3维空间的几何直观出发,抽象出代数的刻画,再将这种代数刻画推广到n维空间,从而建立起n维空间几何学.从3维到n维,从特殊到一般,这一过程很好的体现了马克思主义哲学中认识事物的一般规律,也反映了近现代数学“抽象”的特点.在教学过程中,通过对相关知识点的讲解,引领学生感受与学习抽象化的思维方式,体会马克思主义哲学观在线性代数学科发展中所起的作用.
从马克思主义哲学思想出发,还可以在线性代数多个知识点中深挖思政元素,使学生理解丰富的辩证思想[2].例如在学习矩阵初等变换、矩阵相似变换及矩阵的合同变换时,可以引出“变与不变”的辩证关系.在变化中寻求不变量,这就是“形变质不变”的辩证思想.在判断矩阵是否可逆、方程组是否有解、二次型是否正定时,可以引出“以量定质”的辩证思想.在学习矩阵的可逆与不可逆、向量组的相关与不相关、方程组的有解和无解时,可以引出“对立和统一”的辩证关系,等等.
线性代数的发展历程和知识体系,深刻体现了人们认识事物的一般规律,从多角度探寻事物本质的过程.正如爱因斯坦所说:“问题不能在发生的同一层面得到解答”.正是这样的过程使得线性代数的知识体系不断完备,并发展出了更多深刻的理论,而这些理论由于其抽象性和深入性在分析与解决问题的过程中具有无与伦比的威力.由此,鼓励学生用马克思主义哲学观武装头脑,探索问题的本质,而不仅仅满足于某个特定的解决方法.这不仅是自然科学如今繁荣昌盛的主观动因之一,也是人类社会发展的原始动力.
2.2 “文化自信”类——体现在“文化的课堂”
线性代数这一学科的理论基础来源于线性方程组的求解.我国古代数学家在线性方程组的求解问题中取得了辉煌的成就,最早可见于我国古代数学著作《九章算术》中关于“直除法”的论述.《九章算术》成书于公元一世纪左右,彼时我国古代数学家已对较为复杂的线性方程组问题展开了研究,并且得到了行之有效的求解方法,而西方在线性方程组的研究上直到17世纪才由莱布尼兹建立了完整的理论体系.我国古代数学家在这一问题上的研究早于西方一千余年,这是非常值得骄傲的伟大成就.
在教学中,通过回顾历史,使学生认识到,中国古代的数学研究不仅开展的较早,在一段时间内处于世界领先地位,并由于其注重实用的特点,将丰硕的研究成果直接服务于生产实际,在一定程度上造就了中国古代文化与经济的辉煌.同时也使学生体会到,在我国的传统文化中也有数学科学浓墨重彩的一笔,以此增强学生的文化自信与民族自豪感,鼓励学生探寻我国传统文化中的瑰宝遗珠.
当然,也需要引导学生辩证的看问题.我国古代数学的发展尽管受到生产实际问题的大力推动,但也掣肘于实用至上的研究特点,导致古代数学家未能实现从具体到抽象的突破,在数学研究上还是停留在了“术”的层面,因此错失了发展出现代自然科学体系的良机.提高这方面的认识能够促使学生在学习过程中理论与实践并重.
2.3 “实际应用”类——体现在“实践的课堂”
数学不是无源之水,无本之木.线性代数产生于实际问题,发展出成熟的理论后出现了更为意义深远的应用.在教学中,通过设置实践作业,分享阅读材料等多种形式,使学生了解学科的应用和发展,并鼓励学生学以致用,报效祖国.
在学习矩阵的特征值和特征向量理论时,将“The $25,000,000,000 Eigenvector: The Linear Algebra behind Google”[9]这篇文章推荐给学生阅读.文中对Google搜索引擎的PageRank排序算法进行了详尽的介绍,很有启发性.该算法是诸多搜索引擎的算法基础,深刻影响着互联网时代每一个人的生活.而发明这种算法的拉里.佩奇与谢盖尔.布林当时仅是斯坦福大学的研究生.这是非常贴近学生的应用实例,在讲解理论的同时适当引导,激励学生打好理论基础,并大胆实践,勇于创新.
在讲解矩阵乘法时,向学生推荐了“希尔密码算法原理分析”[10]这篇文章.通过阅读希尔密码的相关知识,学生深刻认识到,简单的矩阵乘法也可以成为深入理论和方法的源泉,从而大大增强了学习兴趣,也了解到应用所学知识解决实际问题的方法和途径.
线性代数也广泛应用于力学、化学、大数据科学、系统分析、图像处理等多个方面[11].通过推荐阅读相关的科普文章,使学生体会到,在实际应用中,人们未必采用的都是十分高深的数学工具,而往往是抓住了某个问题的痛点与盲点,并巧妙的将代数知识应用其中,这正是我们希望学生所具备的善于发现问题的能力与敢于学以致用的精神.对于广大理工科学生而言,学习数学课程并非仅仅为满足专业所需,而更多的是通过对数学思维的培养和锻炼,使其成为受益终身的个人素养,在分析处理问题时去粗取精,把握核心矛盾,将数学知识运用在抽象而本质的框架中,从而成就自我,实现理想.
3 教学效果
文中所述的具体案例和实施办法,笔者已经在东南大学线性代数思政示范课教学班进行了两轮实践,取得了很好的效果.从问卷调查的结果来看,同学们对课程思政持欢迎和肯定的态度,并促进了专业知识的学习和理解.

图1 课程思政问卷调查结果
在课程接近尾声的时候,同学们就自己感兴趣的内容撰写了思政小论文,积极反馈了他们在课程思政中的收获和体会.有的同学从线性代数的学习中感悟到人类认识自然的一般方法:“人类的知识积累就像是一个圆圈在一个更大的闭合圆圈中不断扩张的过程,我们由目之所及,出于好奇心的引领,思考其本质,探究其内涵,就像是在人类知识的圆圈的边界不断试探,当你发现事物的本质时,人类的认知范围也就随之扩大.”有的同学查阅了古今中外数学家在线性代数中所取得的成就,备受鼓舞,从中学习到刻苦钻研和锐意创新的精神.有的同学以思辨的思维看待历史上已取得的数学成就,对当代数学的发展做了一些思考.也有的同学深入挖掘了线性代数在生产实际中的应用,例如结合自己在高中化学竞赛的经历,深入探讨了线性代数在分子对称性中的应用;又如通过向量夹角的几何含义,挖掘出向量夹角在公司筛选简历上的应用,等等.
课程思政与专业知识的有机融合,极大地提高了同学们的学习兴趣.课堂上低头玩手机的同学变少了,课后在QQ群里参与讨论的同学变多了.正所谓“兴趣是最好的老师”,同学们的期末成绩也从一个侧面体现了课程思政对学习的促进作用.从2020年秋季学期笔者的思政示范课教学班(两个班共222人)与全校(共1903人)期末成绩的对比图可以看出,思政示范课教学班的成绩明显优于全校平均成绩.
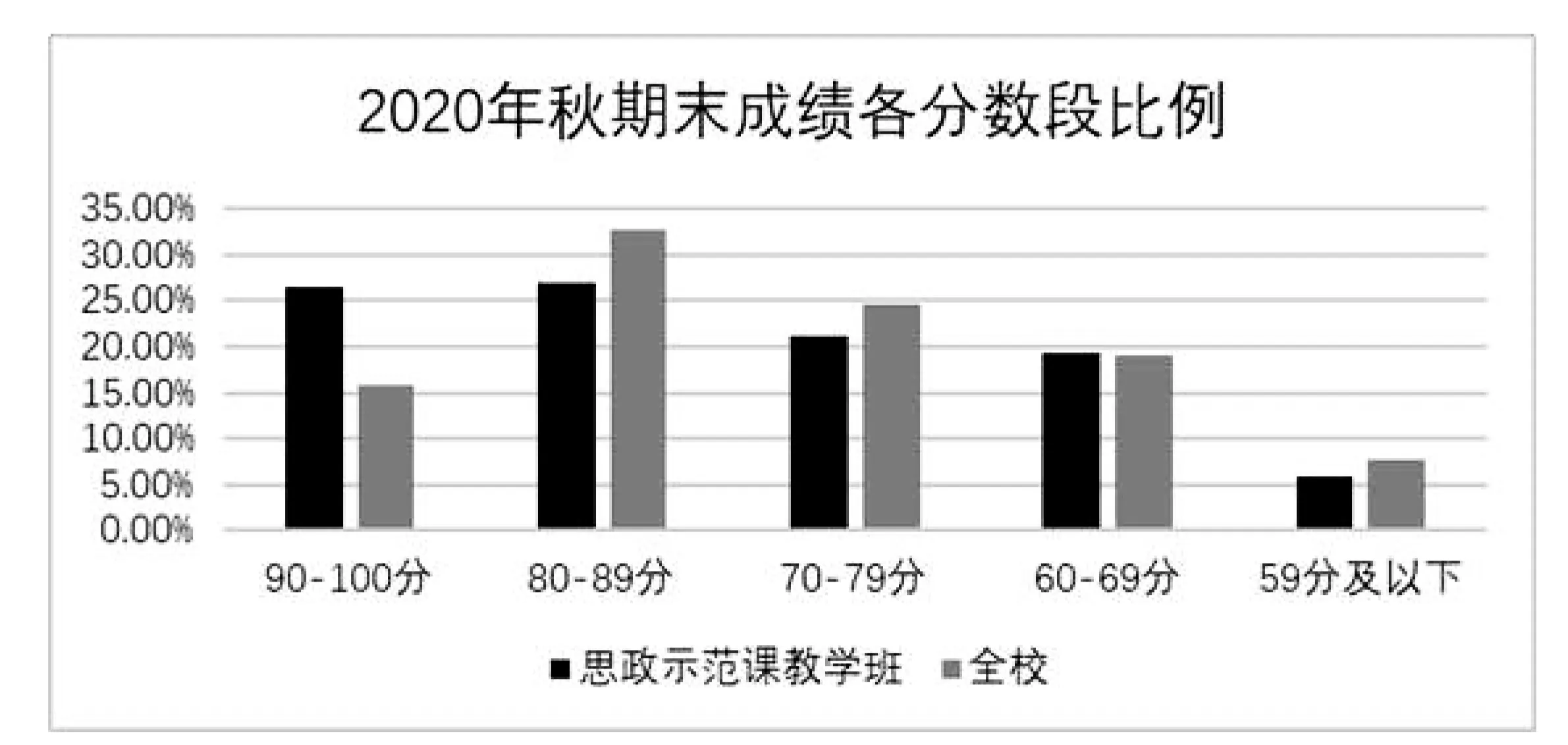
图2 思政示范课教学班与全校成绩对比
4 结 论
古人云:“为学须先立志.志既立,则学问可次第着力.立志不定,终不济事.”线性代数课程思政正是通过具体的思政教学案例,帮助学生树立远大的理想目标,将个人发展与国家命运紧密结合,并培养学生实现理想目标的能力.课程思政对同学们的影响是潜移默化的,但随之带来的改变可能会使他们终生受益.
尽管已取得了初步成效,但线性代数课程思政建设仍然任重道远.“大学之道,在明明德,在亲民,在止于至善.”我们将继续融会创新,不断拓展线性代数课程思政建设的方法和途径,捕捉学科知识和德育教育元素的最佳结合点,不断总结完善教学案例和教学方法,与学生在“思政”中共同成长,共同进步.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
