基于smoothL1改进的边框回归损失函数
2021-10-30陈孝聪
陈孝聪
(合肥工业大学 数学学院,合肥230601)
1 引 言
目标检测一直是计算机视觉领域内一个基础而又重要的方向,它由目标定位和目标识别两个任务组成.当前主流的目标检测算法可以分为两个方向,两步法和一步法.两步法的经典算法有基于区域建议的Faster R-CNN[1-3]等,一步法的经典算法有基于回归的YOLO[4-5],SSD[6]等.
目标检测任务的损失函数由分类损失和定位损失两部分组成.以Faster R-CNN[3]中定义的多任务损失函数为例,如式(1)
Lp,u,tu,v=Lcls(p,u)+λ[u≥1]Lloc(tu,v).
(1)
Lcls和Lloc分别对应分类损失函数和定位损失函数.Lcls中的p和u分别对应类别预测值和真实值.tu对应类别u的边框预测值,v对应类别u的边框真实值.λ是一个超参数,用来平衡分类损失和定位损失的权重.真实值u只能是0或者1,所以u≥1表示1或者0,这表明定位损失函数只对正样本负责.通常称预测值与目标值差的绝对值大于或等于1的点为离散点,小于1的点为非离散点.平衡上述损失的一个常用方法是,调节两个任务损失的权重λ.但是这会增大离散点的梯度,导致模型对离散点非常敏感,不利于训练.[7]中指出,平均每个离散点对整体的梯度贡献达70%,而平均每个非离散点对整体的梯度贡献仅30%.
目标检测中,通常采用交叉熵作为分类损失函数.常见的定位损失函数采用n范数(n=1,2)形式[8-9].L1有固定的梯度,可以让模型稳定收敛,但需要手动的调整学习率,否则后期很难收敛在极值点;L2在训练初期容易产生梯度爆炸.[2]综合了n范数的优势,提出了smoothL1损失函数(式(6)),该损失函数对离散点采用L1,对非离散点采用L2,有效地避免了L1的不稳定性和L2梯度爆炸的情况.
本文提出一种基于smoothL1的新型边框回归损失函数.在不改变离散点梯度的前提下,自适应地增大定位损失函数中非离散点的梯度,缓解了反向传播中对离散点和非离散点的梯度分布不平衡问题.在PASCAL VOC2007数据集上的实验表明,改进后的smoothL1在Faster R-CNN上精度达到70.8%.
2 基于smoothL1改进的边框回归损失函数
2.1 n范数与smoothL1
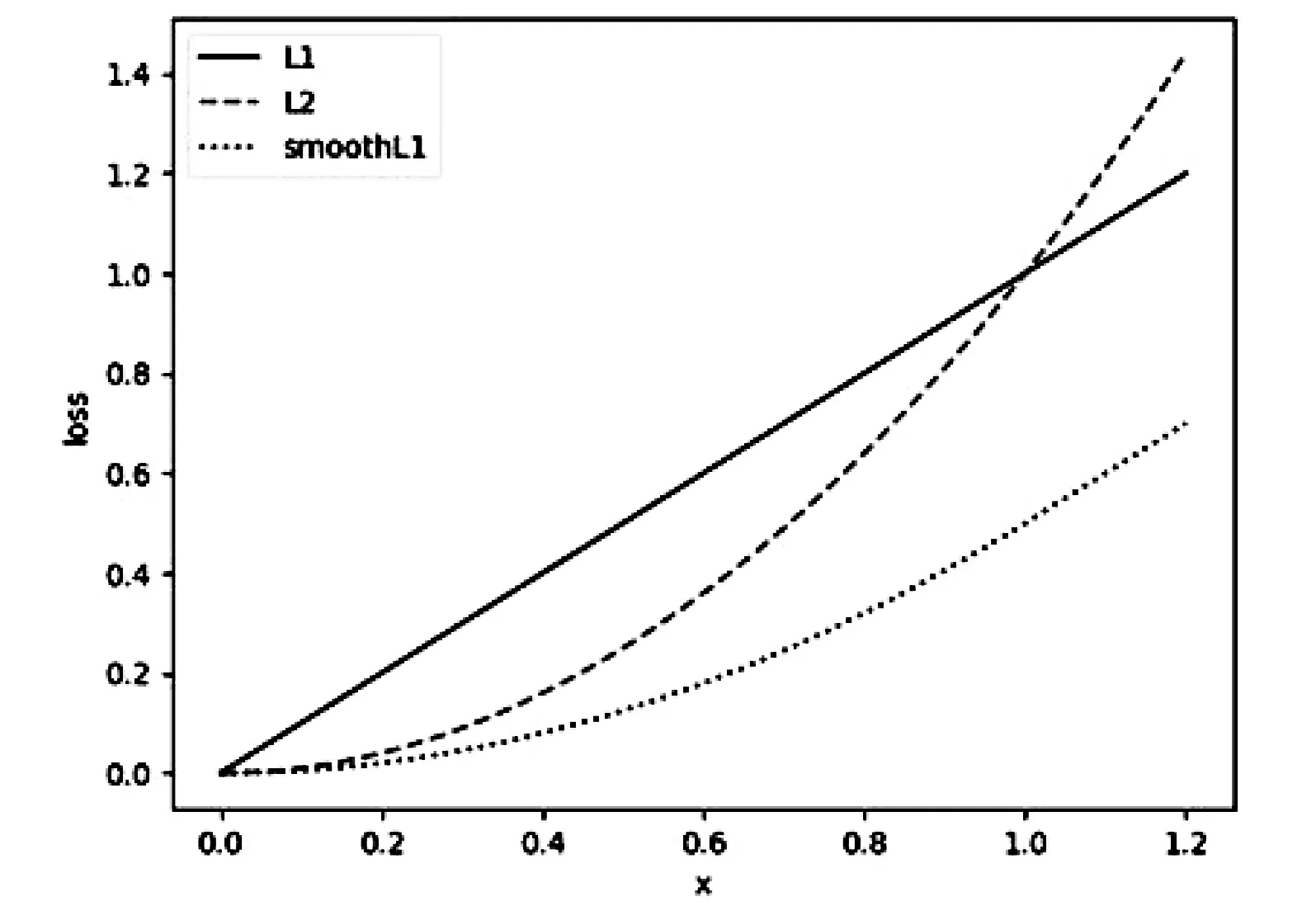
图1 实线表示L1函数图象,虚线表示L2 图象,点虚线表示smoothL1函数图象
L1的表达式如式(2),函数图象如图1,梯度函数表达式如式(3),L1是用来统计预测值与真实值之间差的绝对值之和.可以看到,L1的梯度是一个常量,可以保证模型训练前期稳定收敛,但训练到后期时,需要手动地逐步调低学习率,否则模型将难以收敛.
(2)
(3)
L2的表达式如式(4),函数图像如图1,梯度函数表达式如式(5),L2是用来统计预测值与真实值之间差的平方和.可以看到,L2的梯度随着x的变小而减小,起到逐步降低学习率的效果.但是,训练初期,当x很大时,x的梯度也会成倍的增长,这导致模型难以收敛,并且对离散点非常敏感.
(4)
(5)
smoothL1的表达式如式(6),函数图象如图1,梯度函数表达式如式(7).可以看到,smoothL1对离散点采用L1,可以减少模型对离散点的敏感程度;对非离散点,采用L2,可以起到逐步降低学习率的效果,使模型能够稳定在极小值点处.
(6)
(7)
2.2 改进的smoothL1
为了缓解离散点与非离散点之间的梯度不平衡,提出了改进的smoothL1,表达式如式(8),梯度函数表达式如式(9).可以看到,L1保持不变,L2采用了其等价无穷小的自然指数形式.这样做有两个好处,(i)当|x|趋向0时,smoothL1趋近L2,保证模型训练后期可以稳定在极小值点处;(ii)当|x|较大时,可以自适应地增大梯度.图2(a)展示了smoothL1和改进后的smoothL1的损失函数图象,可以看到,改进后的smoothL1有更大的损失.改进后的smoothL1损失函数的分段点设置在0.65,这样做是为了保证梯度函数的单调性(0.65e0.652≈0.9918),使梯度函数符合这样一个规则,非离散点越靠近真实值,梯度就不增或者越小.图2(b)展示了smoothL1和改进后的smoothL1梯度函数图象,可以看到,改进后的smoothL1自适应地增大了非离散点的梯度.综上所述,改进后的smoothL1相较smoothL1,在不增大离散点梯度的情况下,增大了非离散点的梯度.非离散点越靠近真实值,梯度增加的幅度就越小.
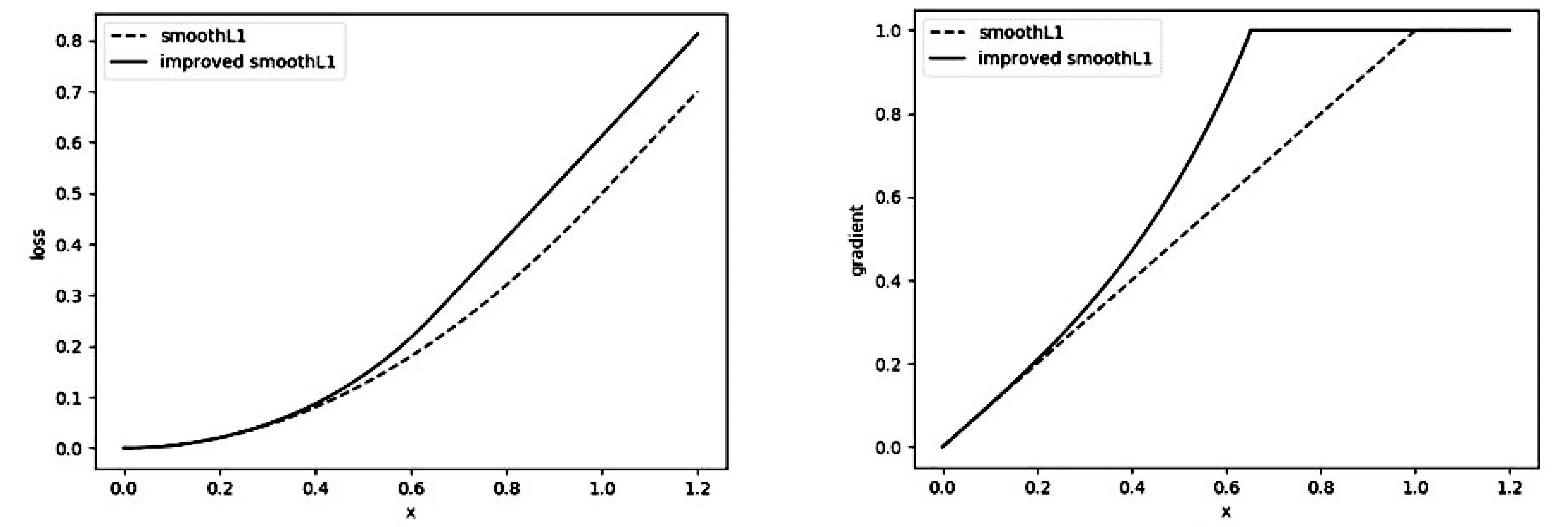
(a) (b)图2 (a) 虚线表示smoothL1的损失函数曲线,实线表示改进后的smoothL1的损失函数曲线; (b) 虚线表示smoothL1的梯度函数曲线,实线表示改进后的smoothL1的梯度函数曲线.
(8)
(9)
3 实验结果与分析
3.1 实验设置
本文在目标检测模型Faster R-CNN上对比基于改进的smoothL1,smoothL1和n范数(n=1,2)的边框回归损失函数的实验,数据集为PASCAL VOC2007,评价指标为平均精度均值(mAP),是目标检测领域最主要的评价指标,mAP越大,表示模型的表现越好.Faster R-CNN采用近似联合训练的方式,训练总共迭代7轮,初始学习率设置为0.001,训练到第5轮时,将学习率缩小10倍,批量大小设置为1.训练前对每张图片水平翻转,达到数据增强的作用.
Faster R-CNN是一个经典的基于区域建议的两步法目标检测模型,模型结构如图3.实验设置的基础特征提取网络为VGG16,通过区域候选网络(RPN)得到候选区域(RoIs),进一步通过候选区域池化(RoI Pooling)得到最终检测结果.
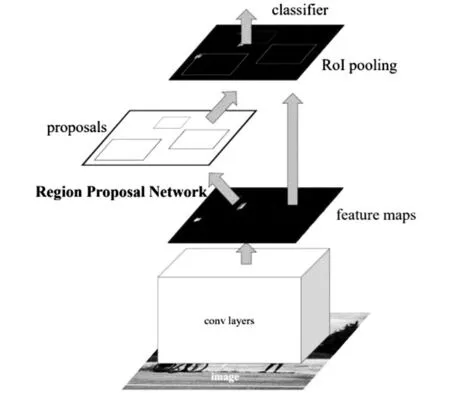
图3 Faster R-CNN模型结构图
PASCAL VOC2007是目标检测领域内最通用的数据集之一,该数据集由5011张训练集和4952张测试集组成,总计9963张图,共包含20个类别物体.
实验环境:深度学习框架PyTorch,GPU为NVIDIA GeForce GTX 1650,显存4G.
3.2 实验结果
3.2.1 模型精度对比
表1展示了不同边框回归损失函数在PASCAL VOC2007数据集上的测试结果.从表中数据可以看出,改进后的smoothL1的mAP达到了70.8%,相较smoothL1,提高了0.2%,基于L1和L2的边框回归损失函数的mAP分别为70.1%和70.2%.对于VOC中的20类不同物体,基于改进后的smoothL1,大部分物体的精度都有所上升.改进后的smoothL1只影响训练期间的梯度大小,没有增加模型的推算时间.

表1 不同边框回归损失函数精度对比
3.2.2 可视化结果对比
图4挑选了PASCAL VOC2007测试集上的一些图片,通过可视化结果对比基于改进的smoothL1和smoothL1的模型检测结果.对比(a),(b),(a)只检测出了一只猫,并且猫的边框还很不准确,(b)检测到了猫和桌子,同时回归框十分准确;对比(c),(d),(c)检测到的两艘船的边框都不准确,(d)准确地检测到了两艘船;对比(e),(f),(e)漏检了一头牛,(f)检测到了所有牛.通过这些可视化结果发现,改进后的smoothL1相较smoothL1,回归框更加准确,回归精度更高.
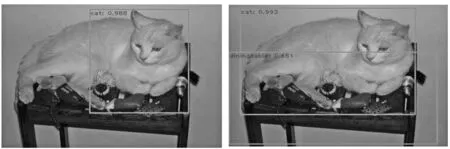
(a) (b)

(c) (d)

(e) (f)图4 PASCAL VOC2007测试集上的运行结果,图片(a),(c),(e)基于smoothL1,图片(b),(d),(f)基于改进的smoothL1
4 结 论
本文提出一种基于smoothL1改进的边框回归损失函数,在不改变离散点梯度的情况下,自适应地增大非离散点梯度,缓解了离散点与非离散点间梯度分布不平衡问题.在PASCAL VOC2007上的实验表明,改进后的smoothL1相较原算法,在精度上有所提升.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
