基于低维流形模型的图拉普拉斯正则化的点云去噪算法

梁 宏

(江西理工大学 土木与测绘工程学院, 江西 赣州 341000)

三维激光扫描技术是获取物体空间点云数据信息的重要手段之一,并在多个领域发挥着重要的作用[1-3]。但是受仪器测量误差、物体反射、遮挡、光照以及环境变化等因素的影响,扫描获取的初始点云数据模型中往往含有大量的噪声点，这些噪声点的数量越多，密度越大，对点云的影响也越大，因此需要采取合适的去噪算法将其去除。

近年来，国内外学者对点云去噪算法进行了较为深入的研究。Rosman等提出了一种通过斑块协同频谱分析对点云去噪的新方法[4]，该方法可以处理高水平的噪声，同时保留清晰的表面特征；Mattei等提出了移动鲁棒主成分分析算法[5]，该方法通过加权最小化保留锐利特征；Sun等提出了L0范数最小化的各向异性化点云去噪方法[6]，该方法可以在大量噪声时恢复清晰的特征；Polat等提出一种LiDAR数据去噪算法[7]，该算法性能可以根据地区地形特征的变化而变化,可以有效滤除非地面点,是一种有效的点云去噪算法。Ma提出一种基于曲面拟合的去噪算法[8]，具有较好的去噪效果和较低的时间复杂度；Wang 等提出一种基于 Laplace 分布的去噪算法[9]，可以有效保留原始数据中有用细节信息；Cruz 等提出一种基于非局域增强卷积神经网络的去噪算法[10]，通过结合卷积神经网络和非局部滤波器实现了图像的有效去噪；Centin 等提出一种几何保真的 Signoroni 网格去噪算法[11]，对目标应用领域具有挑战性的情况去噪效果良好；Zheng 等提出一种基于锐利特征骨架的点云去噪算法[12]，可以有效保持尖锐区域内的几何特征；郭进等[13]提出了一种基于噪声分类算法，可以去除小片噪声；戴士杰等[14]提出了一种各向异性去噪算法，解决了去噪时模型失真问题；苏本跃等[15]基于K-means聚类对点云进行去噪；冯东恒等[16]提出用共面法向量特征去除离群面的RANSAC 算法；许龙等[17]提出了基于模糊C均值和均值滤波的点云去噪算法；林洪彬等[18]提出基于参数自适应各向异性高斯核的散乱点云保特征去噪算法。

为了有效保留点云显著的特征结构信息，进一步提高点云去噪的精度，本文提出了一种基于低维流形模型的图拉普拉斯正则化的点云去噪算法， 通过采用低维流形模型，利用表面斑块的自相似特性，同时对相似的斑块进行去噪，以便更好地保留清晰特征；对流形的大小的计算是通过离散图拉普拉斯正则化器来进行近似的，这大大降低了计算复杂度；针对离散的斑块，设计了一种有效的相似性度量，用于噪声的图形构造。另外本文的图拉普拉斯正则化器具有较好的稳定性。

1 基于低维流形的图拉普拉斯正则化去噪算法

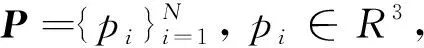
P=U+E

(1)

式中：U,E∈RN×3；U为点云的真实位置；E为噪声(在本文实验中假设为高斯噪声)。为了消除噪声，构建图拉普拉斯低维流形来表示物体在空间域上的几何结构，并提出基于流形的图拉普拉斯正则化下的点云去噪模型。

1.1 低维流形表示

wmn=(ρmρn)-1/γφ(dmn)

(2)

式中，φ(dmn)为高斯核函数，即

(3)

式中，dmn为斑块pm和pn之间的欧氏距离，即

(4)

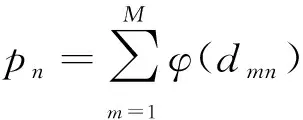
1.2 图拉普拉斯正则化

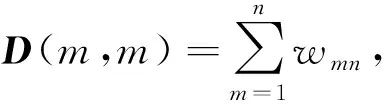
αi(p)=pi, ∀p=[p1,…,p3k]T∈M

(5)

根据文献[13]，流形λ在p点维度计算公式为

(6)

式中,∇αi(p)表示函数αi在流行M上p点的梯度，所以得出

(7)

(8)

(9)

(10)

这样得到了一个逐点收敛的正则化函数，相比较于对整个流形收敛来说，这样更容易收敛。

(11)

(12)

从式(12)可以看出拉普拉斯正则化可以不需要αi函数，因此绕过了对斑块进行排序的问题。根据式(2)可知wmn也是距离dmn的函数，所以最后问题简化成了求解斑块之间的距离。

1.3 计算距离

为了计算第m和第n个斑块的距离，在理想情况下可以把两个斑块内差到两个连续的曲面上，那么斑块的距离就是曲面函数局部区域上的积分。为了方便计算，定义一个参考平面，该平面与斑块的中心相切并且与该点法线垂直。由于不同斑块的法线方向不一样，为了精确计算，在两个斑块上各自计算一次距离，它们的平均值即为所求。

图1 连续表面距离的测量

(13)

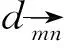
(14)

得到距离为

(15)

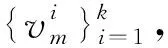
(16)

图2 离散斑块的距离测量

(17)

(18)

但有时，在该点附近找不到最近邻点，这时为了找到与投影点对应的点，采用平面插值方法。对于点v，在另一个斑块上找其对应的插值，找到3个投影距离最近的点形成一个平面，并找出点v沿法线方向在平面上的投影v′，此时计算距离就变得比较容易了。使用投影来找对应关系而不是通过点位置，是因为投影对噪声具有良好的鲁棒性。例如在图3中，两个斑块的表面都是平面，通过投影计算的是垂直的直线距离，如果直接根据点位置计算距离就是水平的连线距离，这样计算会导致去燥效果不佳。

图3 平面插值法

基于上面的斑块测量方法，在不涉及插值时，第m和第n个斑块连接取决于它们在参考平面上的投影，通过求出最小距离的方式找出了两个斑块的最近邻点，但在边上是加权无向的。

涉及插值后，v和a的权重wva定义为

(19)

式中：v为斑块m上的点；点a、b、c为斑块n上的点；dva为点v到a的距离；同理dvb、dvc也是v到点b、c的距离。

为了简化实现过程，设置一个以k为最近邻的窗口，计算出k最近邻斑块之间的距离，而不是直接计算点云中所有斑块的距离。计算完成之后，构造出了一个点域图，给出了图拉普拉斯算子Lp∈RkM×kM，kM为所有斑块的总点数。因此优化可以写为

(20)

(21)

由于拉普拉斯算子依赖于斑块坐标，采用交替优化的方法，在每次迭代中，修复Lp并求解U，然后在给定U的情况下更新Lp，然后重复进行直到收敛。在每一次迭代中，都可以根据之前的方法更新Lp，为了固定Lp优化U，每个点坐标(x,y,z)由下式给出：

(STLpS+μIq)Uq=μVq+STLpCq

(22)

式中：q∈{x,y,z}为坐标索引；Iq为与Lp大小相同的单位矩阵。迭代化求解，直到结果收敛。

2 实验结果与分析

为了验证本文点云去噪算法的有效性，对Anchor、Gargoyle、Lordquas、Dc、Daratech等模型进行测试。采用MATLAB程序编写算法，在meshlab程序上的poisson重建算法对模型进行三维重建，验证了本文算法有助于对边缘特征的保留，不会导致过度平滑。为了加快实现速度，将50%的点当作斑块中心，并使用最远的点采样来确保空间中的均匀采样。将搜索窗口设置为16，将斑块大小设置为30。在图4中使用Anchor模型显示迭代结果，标准偏差为0.01的高斯噪声被添加到点云中。前3次迭代中的结果的表面重建如图4(c)和(d)所示。迭代3次之后的结果收敛，因此只显示前面3次迭代。参数μ=25exp(iteration)-1随迭代增加。与其他方法的比较在图5和图6中，图5中APSS的结果和RIMLS的结果在折叠区域和拐角处过度平滑。另外为了保证本文方法的准确性，对更多的模型进行了测试，将标准差为0.02、0.03、0.04的高斯噪声添加到测试点云中，数值结果显示在表1～表3中，其中本文算法具有最低的MSE。这些模型的参数μ=25exp(iteration/r)-1，其中对于σ=0.02、0.03、0.04的高斯噪声，r=4、7、12。

图4 Anchor模型在σ=0.01的去噪后表面重建结果

图5 Anchor模型在σ=0.02的去噪后表面重建结果

图6 Gargoyle模型在σ=0.03的去噪后表面重建结果

表1 具有高斯噪声不同模型下的MSE(σ=0.02)

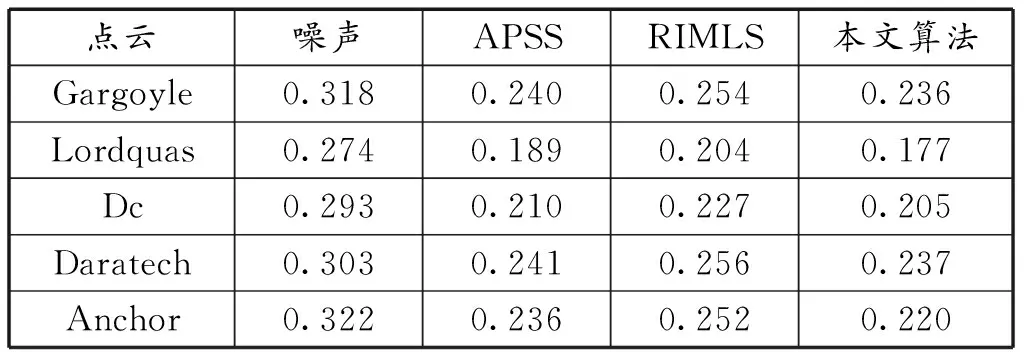
表2 具有高斯噪声不同模型下的MSE(σ=0.03)

3 结论

提出了一种基于图拉普拉斯正则化的3D点云去噪算法。得出以下结论：

1)提出的算法能普遍适用于有显著几何特征的噪声点云，因为该方法针对的不是具体的形状的点云，而是具有这个空间结构的所有的点云。

2)本文算法对比其他算法，在确保去噪精度的同时，能够把物体的边缘特征和显著特征清晰地保留下来，同时不会在表面产生过度平滑。