基于粗糙集-层次分析法的航材供应商选择模型
2021-10-29袁福帅崔崇立王启同
袁福帅, 崔崇立, 程 成, 王启同
(1.空军勤务学院 研究生大队, 江苏 徐州 221000; 2.空军勤务学院 航材四站系, 江苏 徐州 221000;3.空军装备部驻北京地区军事代表局, 北京 100000; 4.空军大兴综合仓库, 北京 100000)
航材部门购置的航材是保障飞机遂行飞行任务的物质基础,而对飞行安全性的要求,航材质量则是最重要因素,质量优良的航材能够保证航材装机使用时发挥其正常效能功用。航材的多样性以及专业性使场站机务人员不可能精通每一种航材的维护修理,因此需要供应商提供优质的售后服务,跟踪航材的使用情况并及时解决在使用过程中出现的问题。对于航材的来源,一种方式是通过修理返回,另一种则是向供应商订货。航材供应商的供应能力能够直接影响场站航材的保障工作效率以及能力,要保证航材部门在急需航材供应时保证采购的航材能够及时补充到达。交货时间越快,越能减少因缺航材飞机停飞的现象。最后,航材筹措工作还要考虑航材费用的高低,要求以最低的成本费用完成筹措任务,从而体现航材保障经济效益[1-2]。
1 层次分析法简介
层次分析法(analytic hierarchy process,AHP)是Saaty于20世纪80年代中期提出的一种系统分析方法,这种方法模仿人对于复杂决策问题的思考、判断过程,构建层次矩阵,量化决策者的思维过程,把人的主观判断用数量的形式表达和处理[3]。它的一般步骤为:①分析提取待评价对象权重因素,构建递阶层次评价指标模型;②在多级递阶层次模型中,同一级要素按照重要性标度准则两两比较确定各要素重要度并构造判断矩阵;③计算评价各因素指标权重并得出对应判断矩阵最大特征值λmax;④进行层次排序以及一致性检验。
2 基于粗糙集理论的知识粒度计算相关概念
粗糙集理论由波兰数学家Pawlak提出,是一种应用于挖掘数据信息的理论。该理论能在不附加任何信息的情况下分析隐藏在数据中的规律,并认为知识由分类决定、知识是有粒度的,这种粒度能够通过等价类表示,而知识的不精确性则是由于知识粒度太大引起的[4]。
2.1 知识库
知识库可以定义为序对K=(U,R),其中R为一族等价关系,对于∀X⊆R,其不可分辨关系为IND(X),表式知识X认知程度所能达到的峰值,而IND(R)则表示知识库K=(U,R)的最高的分辨率、表示程度[5]。
2.2 知识的粒度及计算
在知识库K=(U,R)中,知识R∈R为一等价关系,则有R⊆U×U,知识R∈R的粒度GD(R)为
GD(R)=|R|/|U2|=|R|/|U|2
(1)
式中,|R|表示R⊆U×U的基数。
Rmin=

Dis(R)=1-GD(R)
(2)
同样,有0≤Dis(R)≤1-1/|U|,表示在U中随机两个对象的可分辨能力强弱。Dis(R)越大,表明R的分辨能力越强,否则越弱[6-7]。
若R为知识库K=(U,R)中的知识,U/R={X1,X2,…,Xn},则

(3)
2.3 重要度
在信息系统I=(U,A)中,X⊆A为一属性子集,x∈X为一属性,x对于X的重要度即在X中移除属性x之后可分辨度的降低程度,程度越大,则x对于X越重要。故x对于X的重要度为
Sig(x)=Dis(X)-Dis(X-{x})
(4)
3 基于组合评价的航材供应商综合评价模型
基于粗糙集和层次分析法的组合权重航材供应商评价模型简称为航材供应商评价模型,其步骤如下:
1)依据层次分析法构建航材供应商综合评价指标体系。
2)构建主观判断矩阵S、计算各因素权重值并进行一致性检验。
3)构建客观判断矩阵P并计算各因素权重值。
4)选取μ值并计算各因素的组合权重值。
5)计算得到各个航材供应商的综合评价得分。
3.1 航材供应商综合评价指标体系的构建
通过文献查阅以及广泛调研[8-9],结合航材保障工作实际与经济、军事效益要求,筛选出供应能力、航材质量、航材价格、售后服务、交货时间作为评价航材供应商的5个指标,并依此建立航材供应商评价指标体系模型,如图1所示。
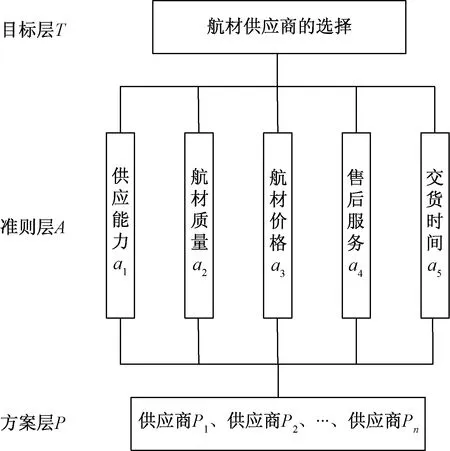
图1 航材供应商评价指标体系层次结构模型
3.2 主观判断矩阵S的构建、权重值的计算以及一致性检验
结合专家打分权重,得出矩阵中的对比标度,在确定评价层次结构模型后,对同一层次的权重指标进行两两比较,其比较结果以重要性标度法表示,各级标度的含义见表1[10]。

表1 判断矩阵标度及其含义
在层次排序步骤使用方根法计算评价指标权重。
1)计算判断矩阵每一行元素的乘积Wi,即

(5)
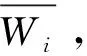
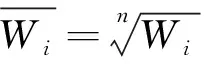
(6)


(7)
则B=(ω1,ω2,…,ωn)T为所求的特征向量,表示为该层次因素对上一层次对应因素的影响程度。
4)计算最大特征值:
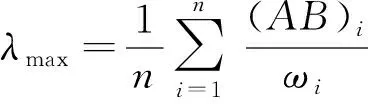
(8)
式中,(AB)i表示向量AB的第i个元素。
5)计算一致性指标CI,即

(9)
6)计算判断矩阵一致性比率为

(10)
判断矩阵平均一致性指标RI可通过查表获得,见表2。

表2 RI取值
二阶矩阵符合一致性要求,二阶以上矩阵若CR<0.1,则符合一致性要求。
3.3 客观判断矩阵P的构建以及各因素权重值的计算
首先,将航材供应商评价体系看作信息系统,图1中的5个指标则为属性集合,即A={a1,a2,…,a5},待评价的各个航材供应商形成系统中的对象集合,对每一个指标进行相应评价并划分为“优”“良”“差”3个评价等级来衡量,分别用3、2、1来表示。
其次,对信息表进行简约,若属性a1、a2∈A对应的评价对象的属性值相同,则认为二者具有相同的分辨能力,只需要保留一个即可。
最后,集合A中属性将样本划分为知识粒,结合评价样本,计算可分辨程度Dis(A)。然后计算各个属性ai的重要度Sig(ai),即将属性ai移除后的知识粒的可分辨程度。
可得准则层中因素ai在航材供应商选择的重要度Sig(ai),即
Sig(ai)=Dis(A)-Dis(A-{ai})
(11)
然后,采用两两比较法,借鉴层次分析法原理,构造出客观判断矩阵P,其元素pij为
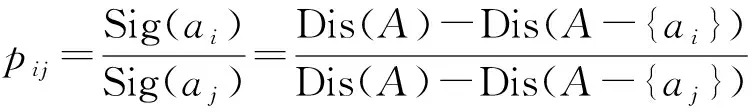
(12)
由于事先对信息系统进行了约简,故任意属性ai的重要度均大于零,因此客观判断矩阵P的各元素pij同样大于零。
同样,依次方法对各指标权重进行计算并进行一致性检验。
3.4 μ值的计算以及组合权重的确定

ωoi≤1,0≤ωi≤1,i=1,2,…,n,建立组合权重模型:
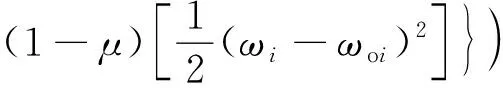
(13)
式中0≤μ≤1。
由求导法可确定组合权重模型有且只有一个解,即
ωi=μωsi+(1-μ)ωoi,i=1,2,…,n。
μ的取值与航材供应商的选取标准比重有关,当专家经验的选取比重高于客观数据时,应有0.5≤μ≤1,当专家经验的选取比重低于客观数据时,应有0≤μ≤0.5。
3.5 航材供应商综合评价得分的计算
结合计算出的权重得到各个航材供应商的综合评价得分S。
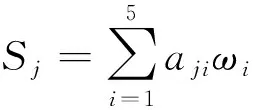
(14)
式中:aji为第j个航材供应商在属性ai的得分;ωi为第i个因素对应的权重;Sj为第j个航材供应商的综合评价得分。
4 实例分析
以下应用粗糙集与层次分析法组合评价航材供应商模型解决实例。
假设Pi(1≤i≤12)是具有竞争力的候选航材供应商的集合,按照层次分析法确定的评价指标体系模型,a1、a2、a3、a4、a5可视为信息系统中的属性,即属性集合A={a1,a2,a3,a4,a5}。候选航材供应商的集合视为信息系统的论域,即U={P1,P2,P3,P4,P5,P6,P7,P8,P9,P10,P11,P12},通过供应商数据样本采集,得到表3。
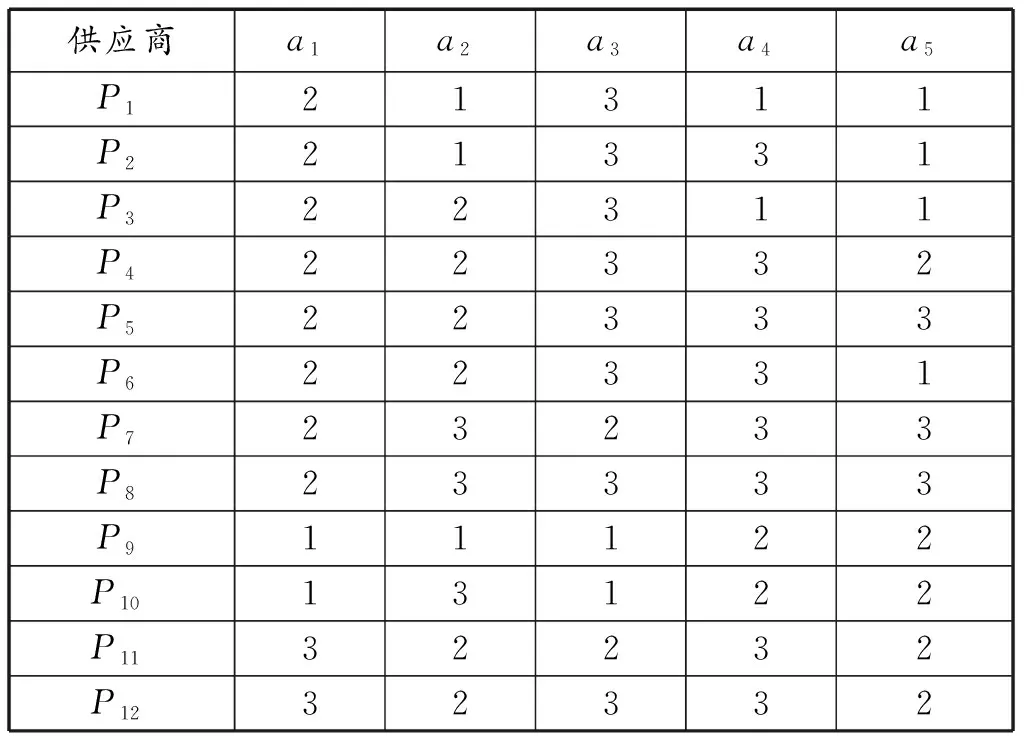
表3 航材供应商指标评价
首先,按照专家打分法得到主观判断矩阵S。

通过方根法计算可以得到主观判断矩阵S的指标权重ωs,即
ωs=[0.174 3 0.373 2 0.121 8 0.081 4 0.087 2 0.249 4]。
此时判断矩阵S的最大特征值λmax=5.165 5,一致性指标CI=0.414,一致性比率CR=0.036 9,符合一致性要求。
其次,计算各属性的重要度并构建客观判断矩阵P。
属性A中所有属性将样本划分成的知识粒的可分辨程度:Dis(A)=11/12。
在属性A中去除属性ai(1≤i≤6)后,A-{ai}将样本划分成的知识粒的可分辨程度Dis(A-{ai}),有
Dis(A-{a1})=65/72;Dis(A-{a2})=62/72;Dis(A-{a3})=64/72;Dis(A-{a4})=64/72;Dis(A-{a5})=63/72。
然后通过公式:Sig(ai)=Dis(A)-Dis(A-{ai})算出属性ai(1≤i≤5)的重要度分别为
Sig(a1)=1/72;Sig(a2)=4/72;Sig(a3)=2/72;Sig(a4)=2/72;Sig(a5)=3/72。
从而通过两两比较法构建客观判断矩阵P。

通过方根法计算可以得到主观判断矩阵P的指标权重ωo,即
ωo=[0.083 3 0.333 3 0.166 7 0.166 7 0.087 2 0.250 0]。
此时判断矩阵S的最大特征值λmax=5,一致性指标CI=0,一致性比率CR=0,符合一致性要求。

最后计算得到论域U中12个航材供应商的综合评价得分,见表4。

表4 航材供应商综合评分
由表4可以得到12个航材供应商的评价得分大小排序为P8、P7、P5、P12、P4、P11、P10、P6、P3、P2、P1、P9。由此可以得出最佳航材供应商为P8。选择结果与客观事实相符,供应商P8除了供应能力稍逊色外,其余指标均优秀,而在供应商指标权重排序中供应能力是最后要考虑的影响因素。
5 结语
综上所示,粗糙集与层次分析法组合权重评价模型适用于实际航材工作中,结合供应商评分数据的客观性以及专家打分的主观性,对二者得到的权重进行组合,得到综合评价权重,最后对各个航材供应商进行综合评分。实例表明此方法是切实可行的,有效地提高了航材供应商选择方面的准确度,弥补了粗糙集方法以及层次分析法两种方法过于偏向主、客观的不足。
