基于神经网络的建筑业碳排放强度预测——以京津冀为例

张广泰， 彭 瑞， 倪平安， 邓舒文

(新疆大学 建筑工程学院， 乌鲁木齐 830049)

碳排放是影响温室效应的重要因素，根据CEIC(China Entrepreneur Investment Club)的数据显示，中国碳排放量一直处于世界髙位[1]。建筑业是国计民生的支柱产业，其全过程能耗总量为全国能耗总量的46.5%[2]。碳排放强度既能代表节能减排目标的实现程度和边际成本，又能简单直观地测算碳排放效率和表示低碳发展的趋势[3]。建立可靠的模型预测碳排放的增长，可指导政府制定环保政策，利于实现节能减排的目标。

目前，学者们多研究碳排放强度的核算和影响因素。 Shahbaz等[4]基于STIRPAT模型，引入技术、人口等变量，分析城镇化对碳排放的作用机理，得出城镇化和碳排放呈“U”形关系。宋金昭等[5]运用LMDI模型，构建了建筑业碳排放强度测算模型，表明能源结构和能源强度效应对碳排放强度贡献较小。武敏[6]借鉴GTWR模型，揭示建筑业碳排放强度的发展机制，并确定能源强度、劳动效率、城镇化水平等因素的作用效果。Bhattachary等[7]通过俱乐部收敛效应，研究了70个国家的碳排放强度，结果显示增加生产率、城镇化率等能提高加入低碳排放强度俱乐部的概率。

然而，上述模拟碳排放强度的变量是非平稳、非线性的，研究者多采用传统的统计学方法和计量经济学模拟这种复杂的行为，如STIRPAT、LMDI模型等，存在精确度不高、变量数目较多、采用公式难以统一等问题[8]。鉴于此，为减少碳排放强度影响数目和提高精确度，有效预测碳排放的未来发展趋势，制定适当的环保政策和战略。本文依托京津冀建筑业相关数据，建立了神经网络模型来预测碳排放未来发展趋势，为实现2035年远景目标提供有效措施和合理建议。

1 神经网络模型建立

神经网络是一种将样本原空间的特征逐层迭代变换到新特征空间，求出符合误差要求结果的模型[9]。兼顾检测精度和检测效率，如图1所示，选择ReLU函数f1(v)=max(0,v)为输入层的激活函数，Softmax函数f2(v)=vg/∑hvh为隐含层的激活函数，均方根误差RMSE为模型的损失函数，构建神经网络模型。其中：

(1)

(2)

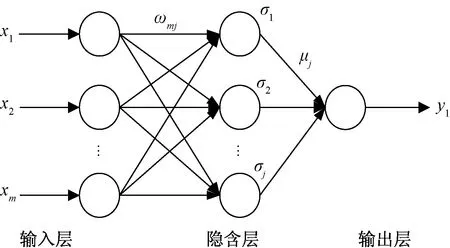
xm为输入变量即碳排放强度影响因素；ωmj为权重；σj为加权输入；μj为活动阈值；y1为输出变量即碳排放强度图1 BP神经网络结构

1.1 参数识别

根据现有研究[6,10]，综合考虑因素的随机性和差异性，筛选易于量化的变量，最终得到13个影响因素：地区生产总值、建筑业总产值、建筑业资产合计、建筑业碳排放总量、年末常住人口、建筑业企业从业人员、城镇化率、建筑业企业技术装配率、建筑业劳动生产率、建筑业企业单位数、建筑业国有企业单位数、建筑业房屋施工面积、建筑业房屋竣工面积。

为避免影响因素过多造成多重共线性，降低预测精度，故应用逐步回归分析与神经网络相互结合的方法，使用最少的合适因素，最大化得出最优的回归模型[11]。加入1个偏置常数，保障充分考虑影响因素间的相互性和独立性。对每次引入的变量都逐个进行赤池信息准则AIC(Akaike information criterion)和贝叶斯信息准则BIC(Bayesian information criterion)检验，确保模型拟合较好。

如图2所示，构建405组模型，最终筛选出地区生产总值A、年末常住人口B、城镇化率C、建筑业总产值D、建筑业企业单位数E和建筑业碳排放总量F等6个影响因素作为输入变量，此时AIC和BIC绝对值不大于15，拟合优度R2≥0.95，具体数据见表1。

表1 预测京津冀建筑业碳排放强度的相关数据

续表1

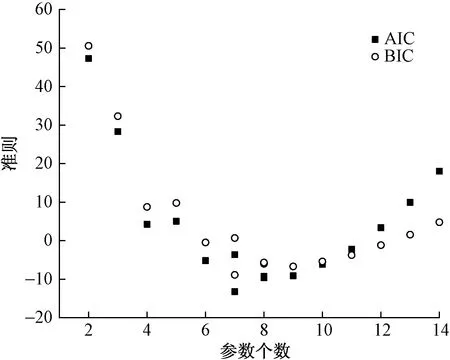
图2 不同参数个数时AIC和BIC的值

fAIC(m)=2m-lnL

(3)

fBIC(m)=mlnn-2lnL

(4)

(5)

式中：0≤m≤13为模型参数个数；L为似然函数；n=30为样本数量。

应用逐步回归分析得到下列公式，可精确计算碳排放强度。

ypredict=α1A+α2B+α3C+α4D+α5E+α6F+K

(6)

式中：α1=5.95×10-5；α2=-1.06×10-3；α3=-16.39；α4=-9.49×10-5；α5=7.23×10-4；α6=5.91×10-5；K=13.63。

1.2 模型训练与验证

为充分利用训练样本，得出最优解的同时，避免欠拟合和过拟合的现象，采用五折交叉验证训练模型[12]，利用网格搜索策略，降低复杂度，提高模型可靠性和稳定性。

将表1中30组数据平均分为5份，借助随机产生的4个折叠子样本数据进行训练和学习，最后剩下的数据用于验证和测试。计算得出的5次结果的均值用于有效估计神经网络模型的精确度，若结果均值较好，则表明此模型在一定程度上有泛化能力，可简化模型为最佳模型，具体流程如图3所示。不断调整神经元个数，由表2可知，选择12个神经元个数时，R2较高，RMSE较低，其精确度可达99%左右，训练和验证的残差绝对值不高于0.12。如图4所示，此时是相对最佳预测模型。

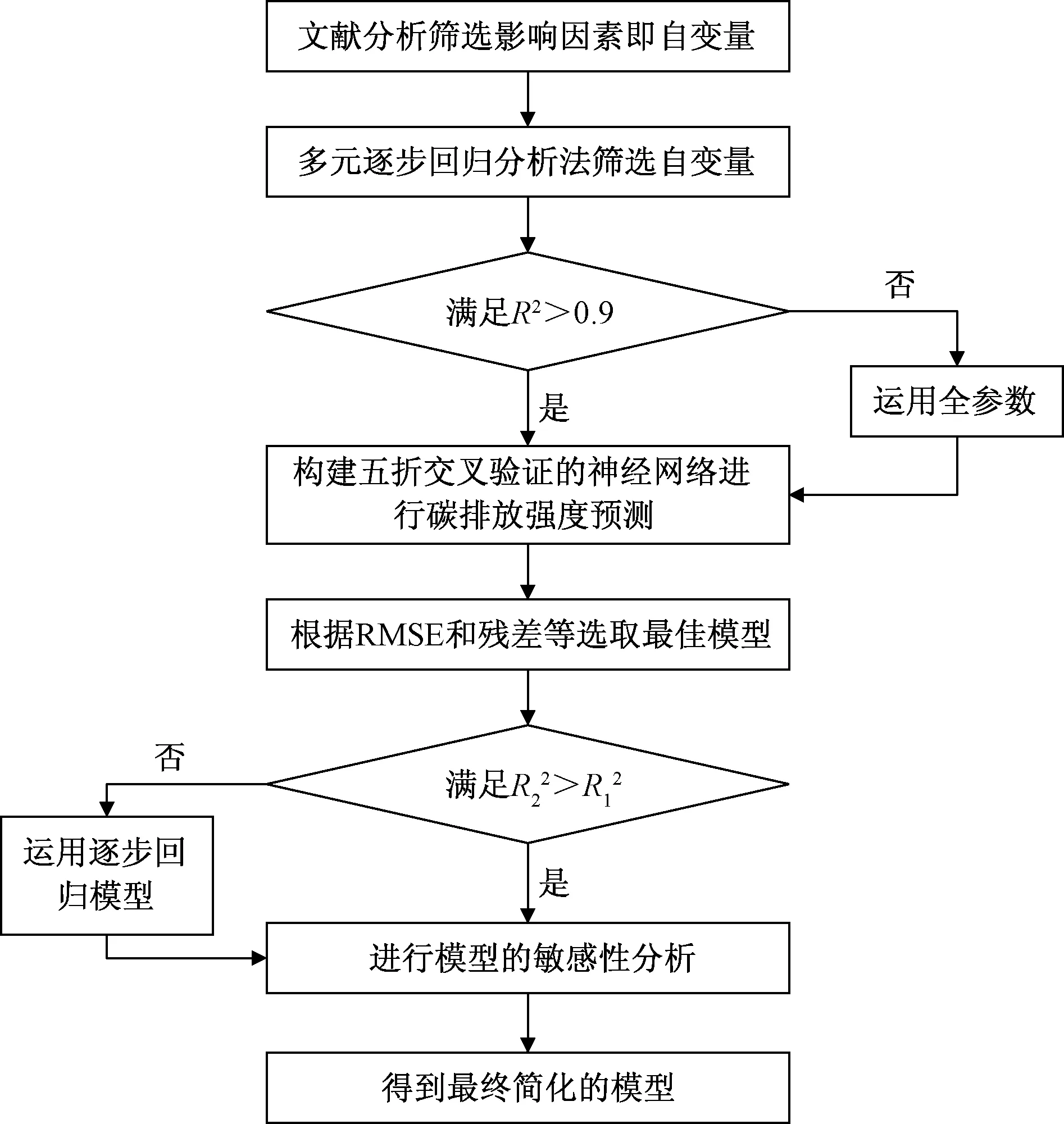
图3 最优模型选择流程

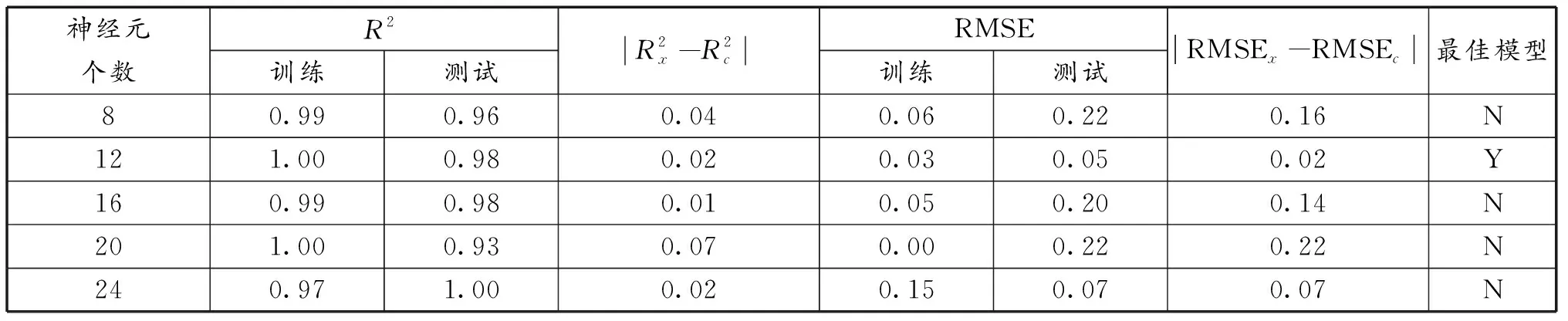
表2 不同神经元数量构建模型对比

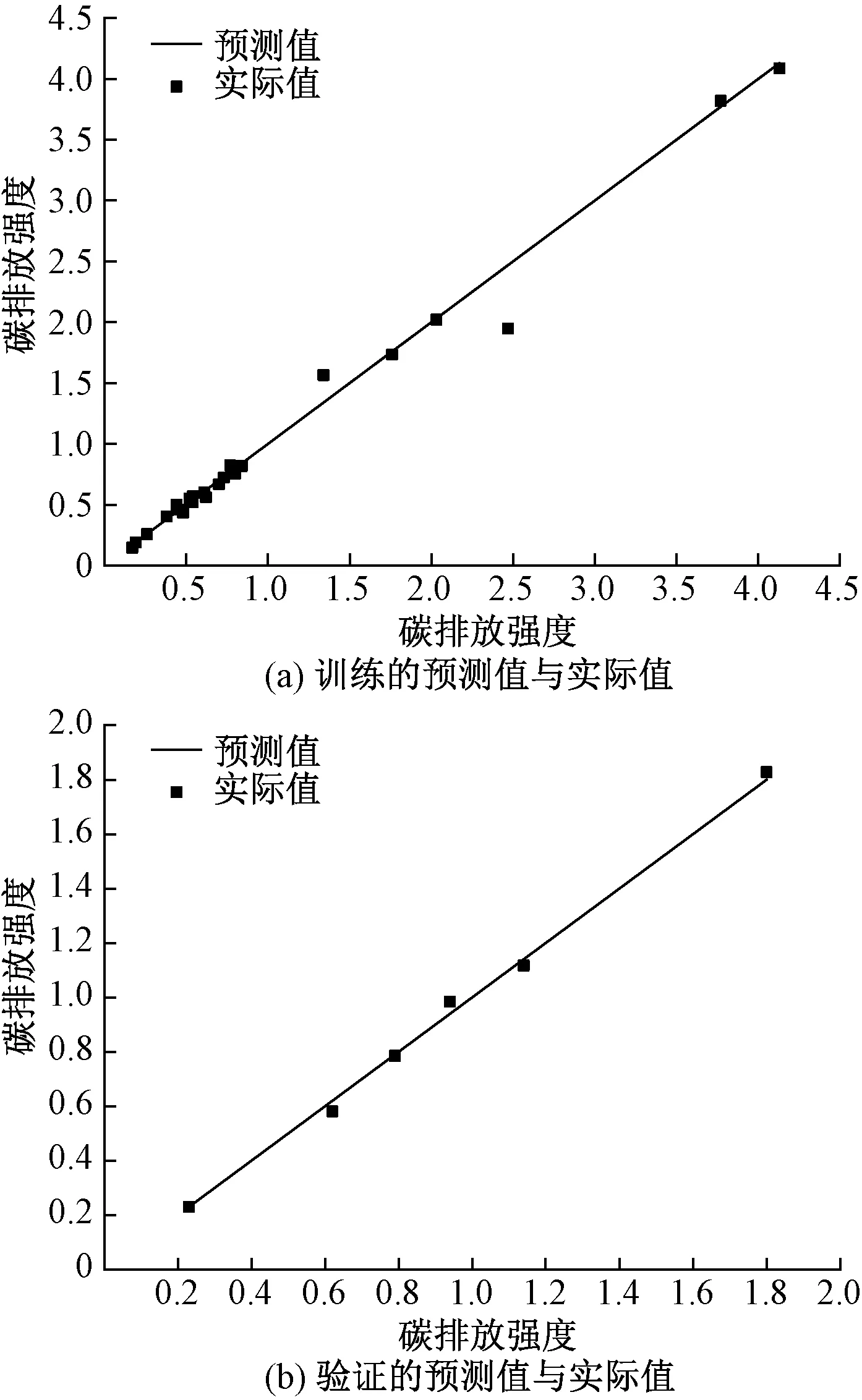
图4 最佳神经网络预测值与实际值的分布

2 数据结果与分析

2.1 敏感性分析

由于神经网络模型有黑箱属性，往往使研究者陷入精确度虚高的风险中。利用敏感性分析，定量分析模型中每个输入信息对输出结果的重要程度，实现模型的审核[13]。其核心思想为分析模型输入变量的属性，求出各属性敏感性系数的大小，令每个属性都在合理的可能的范围内浮动，压缩工作量。

考虑到变量间的相互作用对结果的影响程度，为增强各输入变量对输出变量敏感性系数的稳定性，提高计算速度，简化操作流程，减少模型不可行的风险，故应用DMIM(Delta Moment-Independent Measure)的计算方法，观测一阶敏感性指标和全局敏感性指标，评估出相应变量的敏感性程度。其中，一阶敏感性指标表示输入变量对输出变量的直接贡献率[14]。全局敏感性指标能较好地反映出多个输入变量共同的变化下，变量间交互作用对输出变量的重要程度[14]。

如图5所示，一阶敏感性和全局敏感性大小排序为：建筑业碳排放总量F>建筑业总产值D>城镇化率C>年末常住人口B>地区生产总值A>建筑业企业单位E。

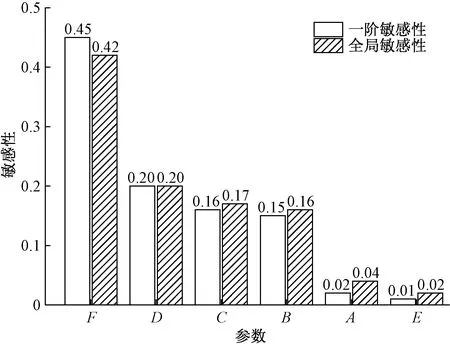
对于影响因素D而言，一阶敏感性为0.198，全局敏感性为0.204图5 一阶敏感性与全局敏感性分析

结果表明，对于京津冀，最核心影响因素有4个。其中，建筑业碳排放量最能直接影响此模型的准确性，对碳排放强度的贡献最多，建筑业总产值、城镇化率和年末常住人口贡献依次减少。设计决策和制定政策时，应优先考虑敏感性较大的这些变量。作为碳排放强度强有力的驱动力，用于驱动京津冀建筑业的发展，有效降低碳排放强度，即以更低的成本获得更高的收益，从而实现节能减排的目标。

2.2 影响因素趋势分析

根据所构建的京津冀建筑业碳排放强度模型预测显示，呈现出最重要的6个变量与碳排放强度之间的相互影响关系。各变量和碳排放强度间的变化趋势如图6所示。

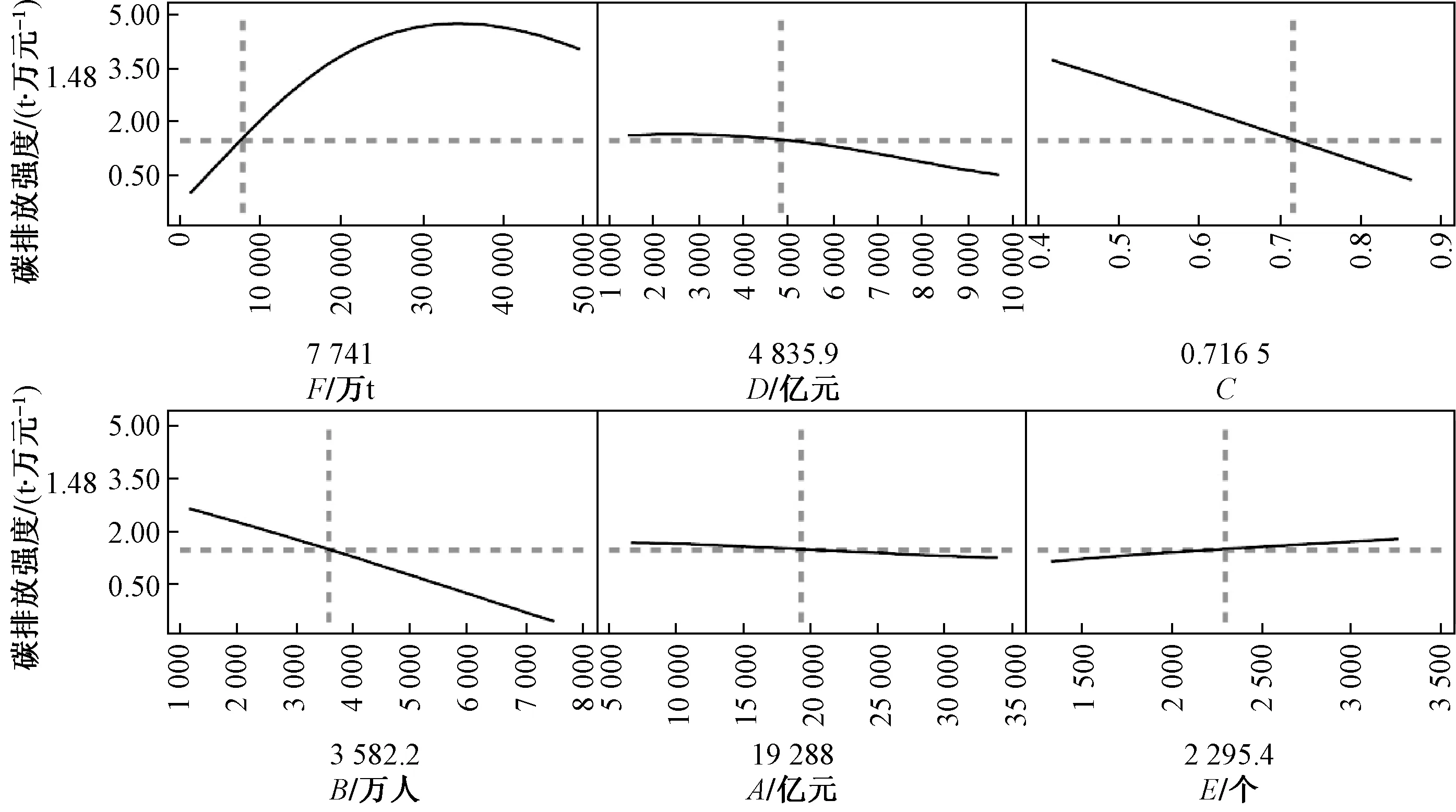
图6 各变量和碳排放强度间的变化趋势

结果表明：

1)能源消耗即建筑业碳排放量F是对碳排放强度影响幅度最大的因素之一，也是为数不多会增加碳排放强度的变量，需要着重关注。随着建筑业碳排放量的增加，碳排放强度的值会先增加后减小。在现有条件下，可通过控制建筑业碳排放量来降低碳排放强度。

2)经济发展是驱动建筑业碳排放强度的重要影响因素，需要加大对建筑业总产值D和地区生产总值A的投入。由D可知，此为一个轻微的弧线，前期影响不显著，后期影响较为明显，可长期投入用于降低碳排放强度。由A可知，此为一条直线，整体变化相对平缓，随着地区生产总值的增多，碳排放强度会逐渐降低，但变化较缓。

3)整体而言，城镇化率对碳排放强度的影响程度较大，稍微提升，就能大幅度影响碳排放强度，需着重考虑城镇化率C，可长期关注并制定一系列政策，以实现节能减排。

4)年末常住人口B是最重要的影响因素，虽然人口增多会产生更多的CO2，但建筑业碳排放强度却逐渐降低，且较为显著。通过综合考虑容积率、资源配比等其他因素，不建议利用人口驱动来降低建筑业碳排放强度。

5)对于建筑业企业单位E而言，是最不能影响碳排放强度的因素。随着逐渐增多建筑业企业单位，碳排放强度也在相应增加，但其浮动范围相对较小。

具体而言，建议通过减少建筑业碳排放量、加速城镇化建设等方面，制定设计规范和规章制度等，从而降低碳排放强度，最终有效减少碳排放。

3 结论

引入神经网络预测建筑业碳排放强度，提出了一种克服统计方法局限性的实用性新方法，为建筑行业碳排放强度的测算提供了思路。借助逐步回归分析筛选关键影响因素，确定了地区生产总值、年末常住人口、城镇化率、建筑业总产值、建筑业企业单位数和建筑业碳排放总量等6个因素。通过五折交叉验证，选取最优的模型，训练并验证近年京津冀建筑业碳排放强度，最终利用敏感性分析简化模型，指出建筑业碳排放总量、建筑业总产值、城镇化率、年末常住人口、地区生产总值、建筑业企业单位和建筑业碳排放强度间的变化趋势。结果表明，此神经网络模型，在预测以京津冀为例的建筑业碳排放强度方面是有效和可靠的，预测误差较小。同时，建筑业碳排放总量的敏感性权重最高，地区生产总值敏感性权重最低，在制定建筑业相关政策法规时要注重影响较大的因素，才能更好地控制建筑业碳排放问题，保护环境。