浅谈培养学生几何直观能力的策略

冯建青

【摘 要】数学学习的知识点既有“数的特征”，又有“形的特点”。高年级学生对数学产生畏难情绪，是因为解题时无法像低年级时期对题目产生直接判断。这种对题目直接判断的能力是不经过逻辑分析的，需要学生具有直观能力，直观能力的养成不是一蹴而就的，需要在各年级的学习中重点

培养。

【關键词】数学学习 几何直观能力 培养策略

关于几何直观，在《义务教育数学课程标准（2011年版）》中强调的是利用图形描述和分析问题，具体内容如下：借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要的作用。笔者认为，几何直观能力强的学生可以对题目产生直接预判，这种直接判断的能力是不经过逻辑分析的，而几何直观能力是一种经验的积累，应在各年级中重点培养。本文基于笔者的课堂经验，阐述了在小学各年级的数学学习中培养学生几何直观能力的重要性，以及培养几何直观能力的策略。

二、以形助教，发展低年级学生识图能力

数学学习是学生思维从直观走向抽象的过程，学生在低年级时应该牢牢打下把数学信息符号化、抽象化的基础。在低年级的教学过程中，教师应着重培养学生观察图片的能力。

1.用数学的眼光观察图片

低年级学生在观察图片时随意性大，识图时没有重点和方向，随着自己的兴趣来看图，得出的看图结果往往是片面的，容易遗漏重要的数学信息。例如，苏教版数学二年级上册第三单元《表内乘法》第1课时，学生在看教材中的相关图时能直接看出有鸡和兔两种动物，要是问学生“兔有多少只”“鸡有多少只”学生往往会用已有经验一只一只地数，如此就没有达到教学目的了。

教师应先让学生充分观察图片，在学生第一次观察图片得到图中“有2种小动物”的前提下，还要深入识图得到“小鸡3只一堆”“小兔2只一堆”的结果，让学生在图中对应位置标记上“3只鸡”“2只兔”，渗透图片表达的“几个几”的含义，让学生能够列出算式：

鸡：3+3+3+3=12（只）。

兔：2+2+2=6（只）。

学生在总结学习过程时，不仅是根据算式说出有“4个3、3个2”，而且有图片作为依托。学生通过看一看、标一标，才能有效地理解图片表达的信息，在以后识图时，能够用数学的眼光、数学的思维观察图片。

2.用图画代替实物演示

爱动、爱玩是学生的天性，低年级学生注意力持续时间短，在低年级课堂上教师经常会借助实物演示、准备教具学具，让学生在实践中获得数学知识、在操作中发展数学思维。这样将理论和操作相结合是以学生为主体的教学，是新课程标准所提倡的以人为本的课堂。然而许多课堂教学中，教具繁复难以在日常课堂中准备，需要学生拥有几何直观能力，对图片进行简单的加工。例如，苏教版数学二年级上册第四单元《表内除法》第1课时，除了课件演示如何将8个桃子每2个一份平均分，让学生理解平均分的概念，还要让学生动手在图上每2个桃圈一份，一共圈出了4份，就是可以分给4个小朋友。

用图画代替实物，从具体的实物演绎到抽象的几何标记，是学生思维能够达到的水平，也是发展几何直观能力的重要契机。教师只有重视在低年级时培养学生的识图能力，学生才能发展相应的几何直观能力，为中高年级将复杂的题目简单化、将抽象的知识形象化打下坚实的基础。

三、以数解形，发展中年级学生画图能力

在计算时，如果数字大、方法复杂，我们要提倡学生用竖式计算。那么在数量关系越来越复杂、接受的数学知识在生活中不常见时，我们也可以要求学生用画图的方法来梳理数量关系，借助简明、形象的几何图，延伸解题思路，促进学生逻辑思维能力的提升。

1.从简单开始，实现数向形转化

小学生处在形象思维为主的阶段，强迫学生掌握抽象的知识体系，只能让学生对数学学习敬而远之，无法让学生真正成为学习的主人。利用图形几何解析题目，能把复杂的题目简单化、把抽象的题目形象化。不同类型的题目可以画不同的几何图形，比如线段图、立体图、示意图、路程图、思维导图。但是不能为了画图而画图，要让学生用图画、符号来表达自己的意思，比如，苏教版数学五年级上册第一单元《负数的初步认识》中，抽象的负数概念不如正数概念清晰，学生生活中接触得比较少。在建立负数的概念时，教师可以让学生画一画电梯中的楼层示意图，地面为0，地上就是用正数表示、地下就是用负数表示。而把这个示意图放平，那就是数学家所说的数轴了。

学生利用有限的生活经验，画出了电梯楼层的示意图，再在示意图的基础上加以演绎推理得到了正数和负数的概念。这项概念是在学生已有的知识基础上演绎得来的，学生容易接受也容易理解透彻。用几何图形来帮助理解题目，能把抽象的知识跃然纸上，让人一目了然，实现数向形的转化。

2.向复杂过渡，透析数量关系

中年级的数学题目中的量未必庞大，但是数量之间的关系开始复杂化了。这种复杂就像是计算数字较大的乘除法时要用竖式计算，对于较为复杂的数量关系，我们则需要利用线段图来解析，在用线段图来表示时应做到以下两点：

（1）在用线段图时要让学生厘清线段图之间的关系，也就是看图说话、厘清题意。

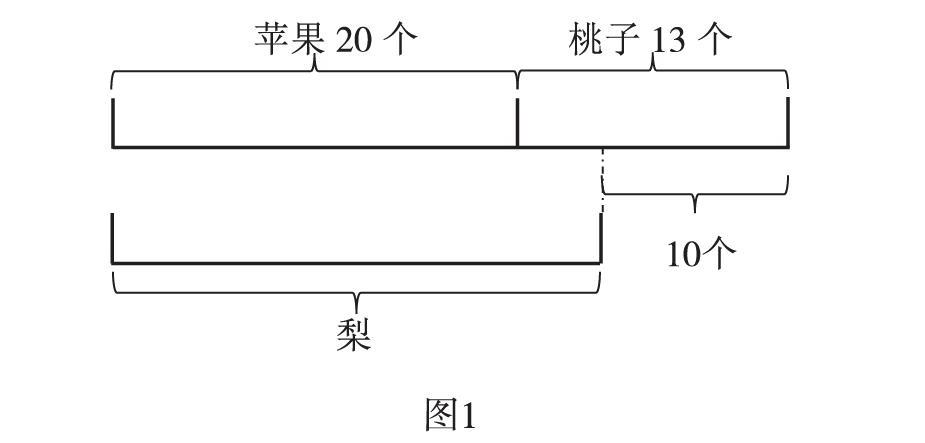
像图1这样关系稍复杂的线段图，要让学生先看懂图，知道“苹果有20个，桃子有13个”，还要能说出数量之间的关系“梨比苹果和桃子的总数少10个”。在线段图中看懂了关键的数量关系之后，再提出问题。有的学生提出问题“梨有多少个”，根据图意解题可以拓宽学生的解题思路。线段图等几何图可以帮助学生梳理数量之间的关系，对结果产生预判，是学生应掌握的解题技巧。

（2）教师要加强中年级学生对于线段图的比较，能在不同的线段图中找到相同点。

数学是抽象的，数学知识点既有“数的特征”，又有“形的特点”，教师要用几何图在直观与抽象之间架起桥梁。例如，当问题“两堆煤共有1440吨，第一堆煤比第二堆多120吨，问两堆煤原来各有多少吨”和“两堆煤共有1440吨，如果从第一堆运送120吨到第二堆，那么两堆煤的吨数一样多，问两堆煤原来各有多少吨”一起出现时，学生总是厘不清思路，不知道这两题的区别。这时需要用线段图来解析，把复杂的数量关系先梳理清楚。第一个问题中，第一堆煤多，比第二堆多120吨;第二个问题中，第一堆煤多，多了两个120吨。第二个问题中“多了两个120吨”比较抽象，需要借助画线段图的方法帮助学生分析题意、增强析图能力。

在中高年级中，由于数量关系的复杂化，学生对题目进行预判越来越难，借助几何图形剖析题意，是学生必须掌握的数学技巧。在中年级应加强学生的画图能力，简单的题目学生能在脑海中直接列出几何图，复杂的题目能落于纸上，再抽丝剥茧进行解答。

四、数形互助，发展高年级学生析图能力

“数缺形时少直觉，形少数时难入微。”代数知识容易计算，但缺乏形象性;几何知识具体且形象，能够便于理解。

1.用几何图梳理思路，在几何图中明确数量关系

苏教版数学五年级上册便开启了代数的新領域，许多教师发现学生难以掌握这个单元的知识点。这论证了代数的抽象性，学生应结合几何图的形象性，从而将代数向几何转化。从几何中抽取数量关系，灵活地将代数与几何互相转换能加深学生对题目的理解。高年级学生能依托几何，灵活进行数形结合，在低中年级识图、画图的基础上水到渠成的养成析图能力。

例如，在苏教版数学六年级上册第五单元《分数四则运算》中，有问题“六年级一班有48人，其中2— 3喜欢跳舞，3— 4喜欢唱歌，没有人既不喜欢跳舞又不喜欢唱歌。既喜欢跳舞又喜欢唱歌的有多少人？”题中总人数已知，学生要学会从分数的角度出发找到分数的“单位1”，喜欢跳舞的人占了全班的2— 3，喜欢唱歌的人占了全班的3— 4。根据这一理解，喜欢唱歌和跳舞的分数“单位1”都是全班人数，即把全班人数看作“1”。于是可以将代数向线段图转换，全班可以分为喜欢跳舞的人和喜欢唱歌的人，但是有一部分重合了，这部分便是题目中所求的“既喜欢跳舞又喜欢唱歌的人”。对线段图再次进行分析，如果把喜欢跳舞和唱歌的人都合起来，总人数是大于全班人数的，得出第二个线段图。利用线段图可以清晰地看出关系式，2— 3+3— 4>1，多出的部分便是“既喜欢跳舞又喜欢唱歌的人数”。（详见图2）

2.借助几何图形理解，用几何图形记忆概念

在苏教版数学五年级上册第八单元的综合活动课程中，学生通过观察、猜测、实验、分析和得出结论，积累宝贵的研究经验。最后在得出结论时，能从语言表达向字母表达转换，赋予字母意义。字母便作为一种概念，印在了学生的脑海中。

像这样根据题目画出几何草图，再根据几何图剖析数量关系式，是高年级常用的解题技巧，也是为学生将来学习更抽象的代数知识打下基础。学生通过识图、画图、析图，能充分理解问题、发现问题的本质，展开直观思维的羽翼。有了良好的几何直观思维能力，学生在将来的学习中一定能够有目标、有顺序地思考问题。

数学学科毫无疑问是一门抽象的学科。学生从入学开始便在学习把知识符号化，将形象的事物抽象化。几何直观能力是学生数学学习必备的数学能力和解题技巧。在提倡学生为主体的课堂教学中，教师要把几何直观能力渗透在日常的数学教学中，把培养学生的几何直观能力作为一种课堂意识，在小学各阶段加以培养。