倍的认识:用“几个几”的视角看世界
2021-10-28周晓林
周晓林


【摘 要】“倍的认识”是学生构建乘法结构的关键课,具有重要的研究意义和研究价值。本文基于关键问题进行教材研读,通过教材脉络的梳理和分析比较,确定了以“倍的认识”构建乘法结构的关键问题是“如何用‘几个几的视角去构建两个量之间的倍数关系”,并设计了相应的学生学习活动对关键问题进行破解,构建课堂教学的基本框架。
【关键词】倍的认识 几个几 关键问题
“倍的认识”作为一节典型课,小学数学教师都很熟悉。这节课之所以重要,是因为它是学生构建乘法结构的关键节点和关键课。在学习“倍”之前,学生头脑中建构的是加法结构,是数量的合并与分解、多与少的比较,未曾学习两个量之间的比例关系。学生在二年级学习“乘法初步认识”时,所学内容本质上还是数量的合并,是同一类量的“等合”,也就是“等量组的聚”,并没有涉及兩个量之间的比例关系的研究。
对两个量或多个量之间的比例关系问题的真正理解需要在学生头脑中建构起乘法结构,而“倍”的学习正是建构乘法结构的伊始,因此“倍的认识”这节课具有非常重要的研究意义和研究价值。
一、教材研读,理脉络
教材首先出示的是一幅主题图(如图1),让学生用数学的眼光去观察,可以看到图中有兔子和萝卜,再进一步,可以观察到兔子中有不同数量的灰兔、白兔和黑兔,萝卜中也有不同数量的白萝卜、胡萝卜和红萝卜。
根据已有的数学活动经验,学生可以进行梳理和归类,把兔子和萝卜进行分门别类,记录各自品类的数量:
萝卜:胡萝卜2根、红萝卜6根、白萝卜10根。
兔子:小黑兔1只,小灰兔2只,小白兔3只。
从这份材料里,学生可以进行合计,计算出萝卜和兔子的总数量,或者进行比较,计算彼此之间的数量差,这些都是学生已有的关于“加法结构”的知识经验。
乘法结构则是一个概念体系,涉及乘法与除法,以及与之相关的倍、最大公因数、最小公倍数、运算律,甚至面积、体积、表面积、速度等概念和定律。学生已经具备了乘法和除法的相关知识,有了比较两个量的比例关系的知识和能力基础。教材随之出现的学习材料(如图2)就是在引导学生探究用“乘法结构”来构建两个量之间的倍数关系。
“胡萝卜有2根,红萝卜有3个2根,我们说红萝卜的根数是胡萝卜的3倍。”教材以举例的方式让学生明白“3个2根”就是3倍。然后让学生自己照样子去描述白萝卜和胡萝卜的关系(如图3)。
从上面两份材料,我们可以看出“倍的认识”作为学生构建“乘法结构”的起始课,其知识和经验的基础是“几个几”。学生在学习“乘法的初步认识”时,已经感受到了“几个几”这样的结构。
图4是“乘法的初步认识”一课,教材中的一幅配图,对比图2与图4我们可以很清楚地发现两者的不同:“乘法的初步认识”是基于同一类东西的“等合”;“倍的认识”是两个量之间的比例关系。我们在计算小火车上小朋友的总数和比较胡萝卜、红萝卜两者关系时,视角都是“几个几”。但是计算小朋友的总数时,“几个几”可以随着数数方式的不同而有变化;比较胡萝卜、红萝卜两者关系时,“几个几”则相对固定,以胡萝卜的数量2根为标准去度量红萝卜的数量,得出有几个2根。
二、厘清脉络,找关键
从前面教材脉络的梳理和分析比较中,我们发现构建乘法结构的关键是用“几个几”的视角去对比两个量之间的关系。因此,这节课的关键问题是“如何用‘几个几的视角去构建两个量之间的倍数关系”。
用“几个几”的视角去观察两个量,构建两个量之间的倍数关系,就需要找到标准量,也就是以什么量为标准去刻画和度量另一个量,这本质上和度量物体是一致的,具有相同的结构。
有了这种度量的意识和视角,除了整数倍之外,相应的几倍多几和几倍少几都可以蕴含其中,与学生已有的度量经验和思想方法沟通融合。
梳理相关“倍的认识”的课例,笔者发现很多教师在上课的时候,着重让学生观察两个量,思考两个量之间有怎样的关系。当学生说出了“甲是乙的2倍”后,立刻设置学习活动,让学生用自己的方式去表达为什么是2倍,描述2倍在哪里。例如,“画一幅图表示:△的个数是□的2倍。”
这样的学习活动可以让学生体会到两个量之间的倍数关系,但是缺乏生长性,会局限于具体的两个量,难以将知识迁移,难以去理解其他的各种各样的量的关系,这也是学生出现学习困难的根源所在。
我们都知道,要建立“倍”的概念,其关键是让学生体会“关系”与“标准”的意义。那么如何让学生体会这种标准的构建呢?如何基于关键问题引导学生建立和体会标准呢?
三、基于关键,研学情
那么,基于这样的关键问题,学生自主构建两个量之间的关系时可能会出现怎样的情况呢?我们就此展开了学生的学情研究,设计了如图5所示的学情研究单。
胡萝卜的根数可以直接用数2来表示,红萝卜的根数当然也可以用数6来表示,学习活动提出的要求是不直接用数来表示,你会怎么说红萝卜的根数呢?那么学生可能会出现怎样的描述呢?我们来看学生的表现:
(1)用乘法:3×2=6,2×3=6,或1×6=6。
(2)用描述:2根分一组,2×3=6;左边3根,右边3根。
(3)画图表达:和画的图一样多○○○○○○、△△△△△△。
(4)圈一圈:两个圈一组,圈3组。
(5)加法表示:3+3=6,2+2+2=6。
(6)和胡萝卜联系:比胡萝卜多4根。
(7)用倍表达:红萝卜的根数是胡萝卜的3倍,胡萝卜=1包,红萝卜=3包,1包=2根,2+2+2=6根。
下面是学生的两份学习作品(如图6和图7):
可以看出,上面的两个学生都能基于“2根”的视角去看红萝卜的数量,图6所示的作品是加法结构的呈现:2+4=6(根)。当然也有2+2+2=6(根)和1+1+1+1+1+1=6(根)两种形式,凸显了“等量组的聚”的特征。
图7所示的作品呈现了乘法结构的特征:2个一组圈在一起,圈了3组,恰好是2×3=6;他还画图表示出3个一组和2个一组的不同方式来描述红萝卜的根数。
通过学情研究,我们发现学生能够用加法、乘法、圈一圈、画一画等方式来描述红萝卜的根数,但是没有凸显基于胡萝卜的根数去表达红萝卜的根数。学习活动的任务不能很好地驱动学生去自主构建两个量之间的内在的乘法结构。
四、基于关键,设活动
基于关键问题“如何用‘几个几的视角去构建两个量之间的倍数关系”和前面的学情研究,为了凸显学生学习活动中要基于一个量去构建和另一个量之间的倍数关系,我们设计了如图8所示的学习活动单。
学习活动采用了度量的形式,驱动学生用“□□”去度量○的个数。两个□在这个学习活动中组成了一把尺子,一把用来度量○个数的尺子。那么,学生对于度量结果会有怎样的表达和描述呢?我们来看看学生的作品。
第一类作品(如图9和图10):
图9清楚地表示出从量2块,到4块,再到6块的过程,用分隔线和类似线段图的方式表示量了3次,所以就有了对应的算式:2×3=6(块)和2+2+2=6(块)。
图10则有所区别,它更突出地表达了度量的次数“一次、二次、三次”,所以就会得到度量结果“3个2”。
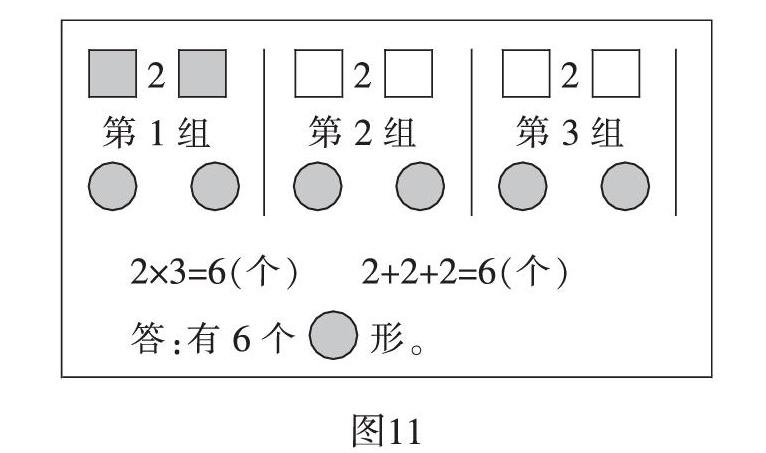
第二类作品(如图11和12):
上面两幅图生动地再现了用2个□去度量6个○的过程,2个2个地量,量了3次,所以有这样的3组,有2×3=6。
第三类作品(如图13和图14):
和前面的有所不同,这两幅图用对应的方式表示○里有“3组相应的2”,把2个□和2个○一一对应去描述。
第四类作品(如图15和图16):
这两幅图相对更为简洁,图15用箭头的方式表示量了3次,所以下面的○被圈成了3组。图16则省略了这一过程,直接用圈一圈的方式表示度量的结果。
从学生的这些作品来看,因为“度量”的任务驱动,量了3次,分了3组,有三个一一对应的量,给学生留下了深刻的印象,他们都在用自己的方式去表达和描述“3个2”,这为接下来“倍的意义”的学习做好了充分的准备。
五、梳理素材,设教学
根据基于关键问题的教材研读和学生研究,在充分解读学生学习活动成果的基础上,我们可以设计基于关键问题破解的教学方案,构建课堂教学的框架。
面对学生在学习活动中展示的素材,我们在进行梳理和分析后,可以借助这些素材,组织学生分类、辨析和评价,在分析和比较中感受“你能用‘□□去‘量一量○的个数吗”这一数学活动的价值。
(一)问题引入
1.出示:□□
看到了什么?你能用一个数来表示□的个数吗?
2.出示:○○○○○○
看到了什么?我们不直接用数来表示○的个数,如果把“□□”看成一把尺,你能用它来“量一量”○的个数吗?
(二)学生活动
1.出示学习活动单(见图8):用你自己喜欢的方式表示你的度量结果。
2.学习活动作品的分享和交流:思考他人是怎么度量的,是怎么表示度量结果的。
3.小结:这些作品度量的结果有什么共同特点?
(都表示出了○中有3个2)
(三)揭示概念
1.引出概念:通过刚才的学习活动,我们知道了□有2个,○有这样的3组2个,我们就可以说○的个数是2个的3倍。
2.想一想,“2个的3倍”还可以怎么说?
引出:正方形的3倍;圆形是正方形的3倍。
3.你能照样子说一说□和△的关系吗?
□ □
△ △ △ △ △ △ △ △ △ △
引导得出:5组2个;2个的5倍,正方形的5倍,三角形是正方形的5倍。
4.概括总结:像这样的圆形有3个2,三角形有5个2,我们就说圆形是正方形的3倍,三角形是正方形的5倍。我们一起来说一说。
引出:这就是我们今天要学习的内容——倍的认识。
(四)练一练
1.圈一圈,填一填。
第二行的個数是第一行个数的( )倍。
第三行的个数是第一行个数的( )倍。
2.把原来的2个□变成3个□。
现在圆形是正方形的( )倍。
3.画一画,填一填。
在学生以“几个几”的视角去观察数学现象的基础上,引导学生用数学的语言来描述世界,用数学模型来构建2个□和6个○之间的关系,凸显2×3的乘法结构和“3个2”的图示形式。当学生明晰了概念,我们就可以让学生用“倍”的结构和方式去观察学习素材,去表达自己看到的数学世界。至于如何用算式来描述和表达两者的关系,这就是下一节课需要研究的内容了。
总之,我们在对教材的梳理和研读中寻找构建乘法结构的关键点,基于“倍”的概念的建立设计相应的学习活动,以关键问题为切入口引领和组织学生展开自主探索、互动交流和汇报讨论,在经历数学学习活动的过程中感受用数学的语言描述生活中的数学现象,学会用数学的眼光观察世界和思考世界。
