基于门控循环单元的铁路客票业务流量数据预测

谢 泽，朱建生，李 雯

(1.中国铁道科学研究院，北京 100081； 2.中国铁道科学研究院电子计算技术研究所，北京 100081)

0 引 言

中国铁路客票系统作为国内唯一的官方火车票销售渠道，自2011年应用互联网售票模式以来，用户数已达5.4亿。在节假日旅客出行高峰期，中国铁路客票系统日售票量可达1 000万张。当系统运行出现异常时不仅会影响乘客的出行体验，还会给社会造成巨大损失。因此，对国内铁路客票系统的异常状态监测显得尤为重要。当前铁路客票系统已实现了全链路监控，其中关键指标阈值监测是最常用的方法。如周期时间内互联网用户登录人数的阈值监控，周期时间内用户支付购票数的阈值监控，以及服务器集群关键性能指标的阈值监控等。但是，在一些异常情况下，如某些服务器响应超时导致的集群崩溃、网络流量激增等，以上独立的关键指标监控可能产生滞后效应，导致预警监测不及时。铁路客票系统业务流量数据能够较为实时地反映系统整体运行状态，为了从整体上对铁路客票系统进行监控，业务流量数据的时间序列预测和趋势预测成为加强异常预警的主要手段。

中国铁路客票系统的业务流量数据主要由用户登录服务数据、车次余票信息查询服务数据、购票服务数据等组成，不同的业务在实现方案中具有一定的串行和并行关系。除此之外，由于售票规则规定小时整点或半点开始售票，业务流量数据在时间维度上具有长短相关性和自相似性。因此，铁路客票系统业务流量数据的预测不同于传统的流量数据预测，如何通过挖掘具有特殊相关性的网络流量数据来提高预测精度成为一个亟待解决的问题。

1 相关工作

流量数据拟合算法已在交通行业[1-2]、互联网金融[3-4]以及临床医学[5-6]等领域广泛使用。基于回归方程的传统统计算法在以上领域很难通过复杂模型实现时序数据的高精度拟合，虽然机器学习算法通过反复训练可以得到比传统统计模型更加精确的预测结果[7-9]，但是当其被用于分析输入变量之间具备强序列依赖关系数据时，性能下降[10]。而具备特殊“重置门”和更新门的GRU神经网络可以通过设定不同的时间步长挖掘滑动窗口内的序列依赖，且该算法易于解构，可依据不同条件改良为适于实际的预测模型，并有高拟合准确度[11-13]。与以上领域建模任务不同，由于铁路客票在售票时刻上存在整点、半点等起售的业务特点，流量数据呈现出历史规律性及突变性。因此选择一个适用于具有复杂、随机特点的铁路客票业务流量数据预测模型，充分解析序列间依赖关系是至关重要的。

文中针对铁路售票时刻特点，选用GRU对铁路客票业务流量数据进行拟合，当该算法时间步长在1至100范围内，步长值分别为1、30、60、90时，对应流量数据拟合结果为局部最优。局部最优的规律与客票售票时间规则形成数据依赖规律相一致，证明GRU适于解析铁路客票业务流量数据。

2 流量数据特性

铁路客票业务流量数据主要由余票查询、用户登录、购票等业务形成的网络流量构成，其中余票查询业务量占全部业务量的60%以上，在单日内其余业务在风控层请求总数都具备明显且规律的凹凸性。如图1所示，该规律与在铁路售票时刻前后有大量用户进行登录、购票等操作的社会行为一致。由于余票查询不需要用户登录，因此余票查询业务在铁路客运业务每日的服务时间内都被用户大量访问，图中展现出余票查询业务对于流量数据总量的变化会有减弱规律特征的作用。

图1 风控层客票业务请求次数统计

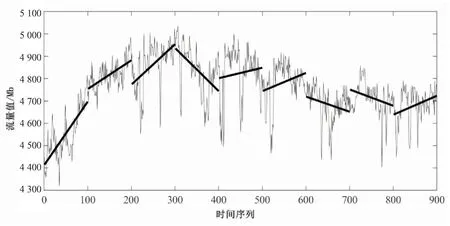
图2为多日流量数据统计，从中可以看出售票规则导致流量数据在数理结构上具有直观的长短相关性、自相似性，短相关性取决于铁路售票时刻规则，长相关性取决于售票规则在长时间段内保持不变。文中选用的GRU神经网络可以通过设定不同的时间步长挖掘滑动窗口内的序列依赖，适于挖掘铁路客票业务流量数据内含的长短相关性及自相似性。

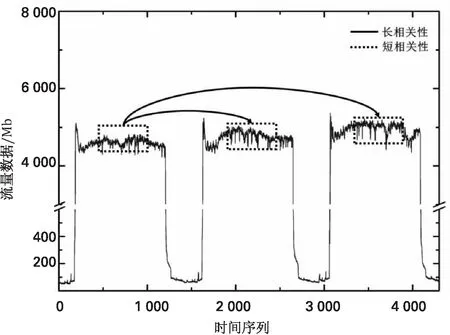
图2 流量数据长短相关性

3 流量数据预测

3.1 GRU算法简介

GRU基于循环神经网络模型(RNN)，解决了RNN求导过程链中连乘导致的梯度消失问题，并且该模型由长短时记忆神经网络进化。图3所示为GRU隐藏层细胞单元的具体展开，Rt、Zt、Ut、Xt、ht分别为重置门、更新门、候选隐藏状态、输入以及隐藏状态，虚线边框GRU重置门模块的结构特性决定该算法适于解决长跨度依赖。由于铁路客票起售规则，所以每30分钟整数倍时间内统计的流量数据之间存在较强依赖关系，GRU时间步长的调节可以改变解析数据间依赖跨度的大小[14]。

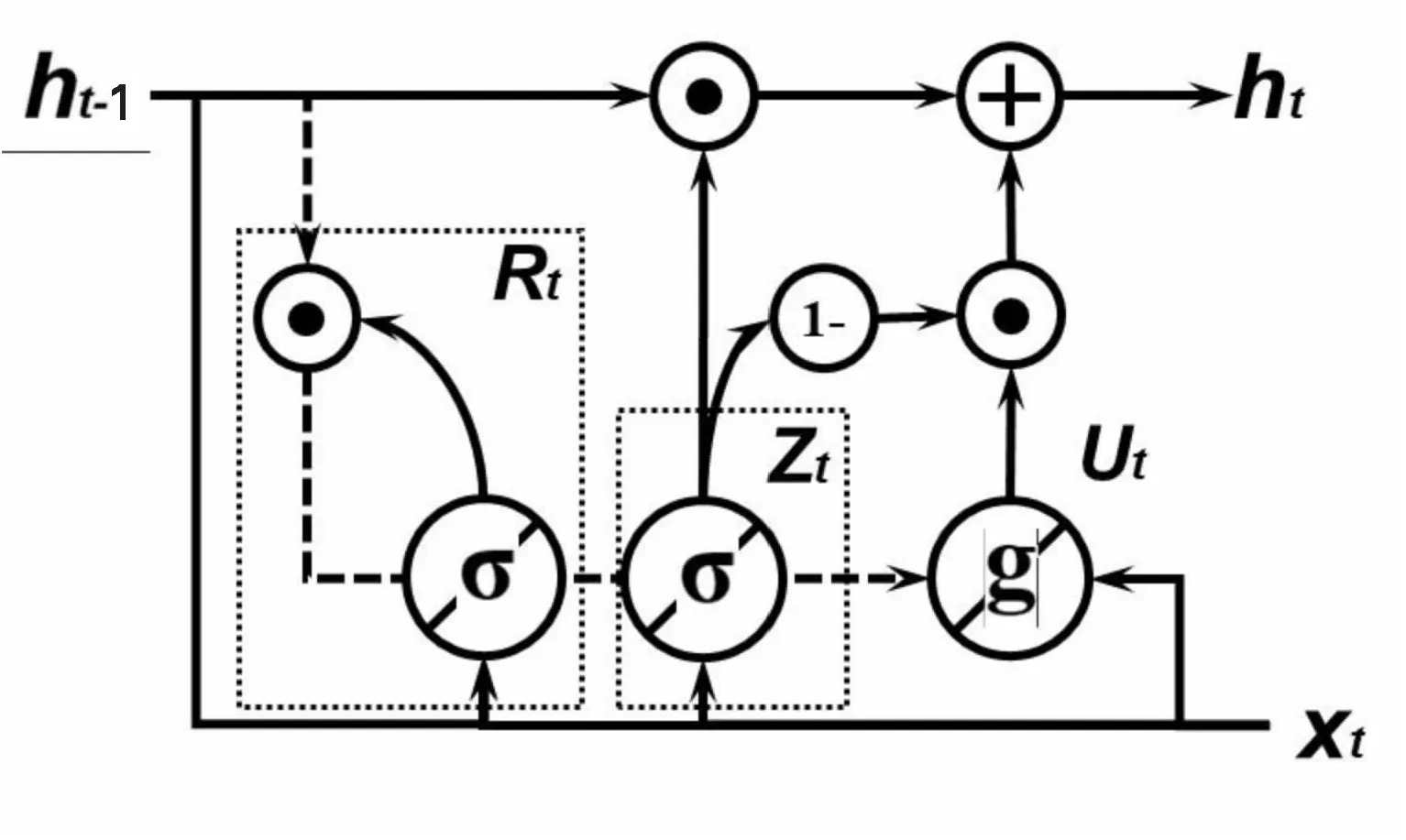
图3 GRU隐藏层细胞单元

GRU隐藏层细胞单元模型的前向计算如下，W和b分别为相应的权重系数矩阵和偏置项，σ为sigmod激活函数，在重置门模块中决定了对之前序列数据的记忆程度，g为tanh双曲正切函数：

Rt=σ(WxiXt+Whiht-1+bi)

(1)

zt=σ(WxfXt+Whiht-1+bf)

(2)

dt=σ(WxcXt+Whc(ht-1⊙Rt)+bc)

(3)

Ut=g(dt)

(4)

ht=zt⊙ht-1+(1-zt)⊙Ut

(5)

GRU模型训练步骤如下：

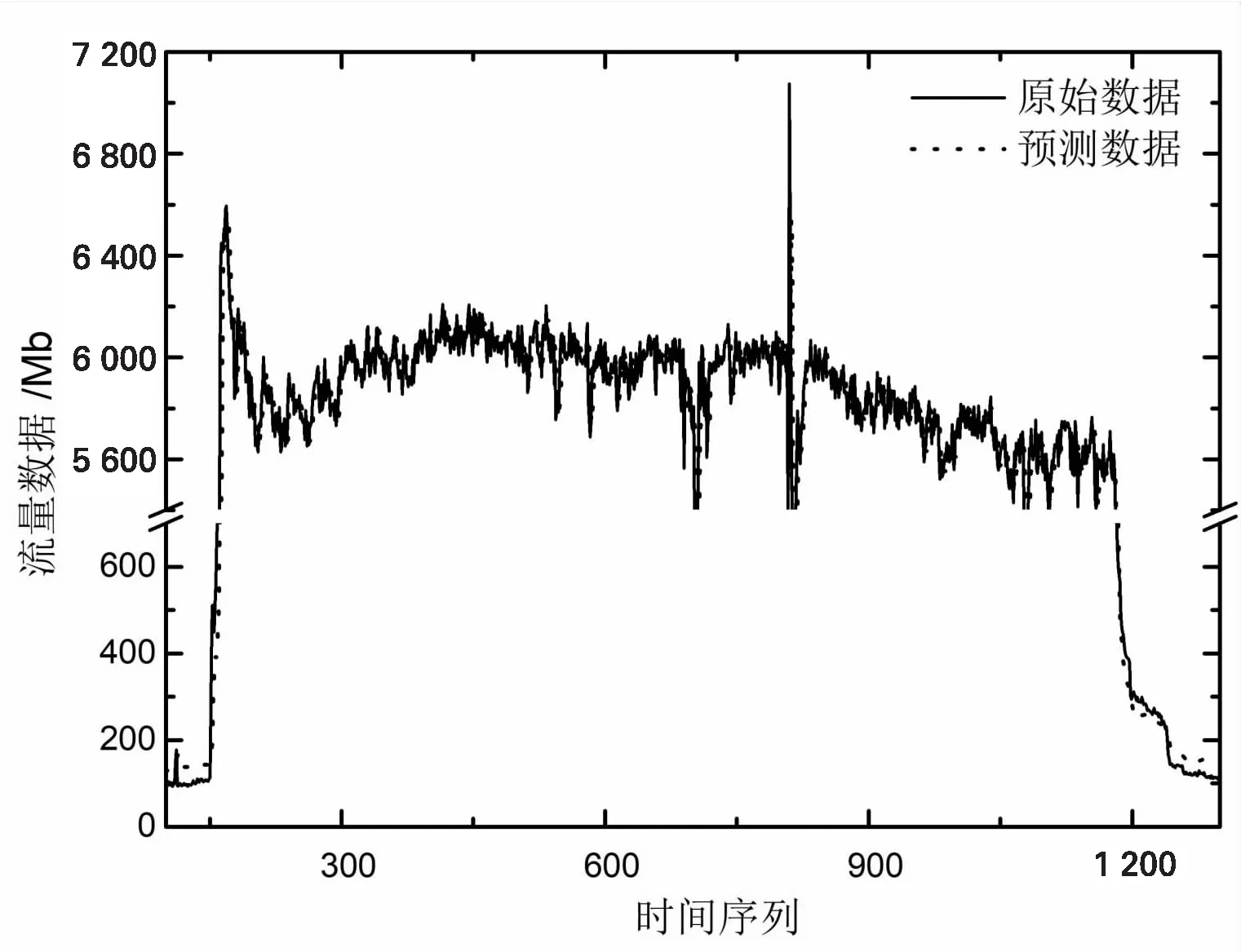
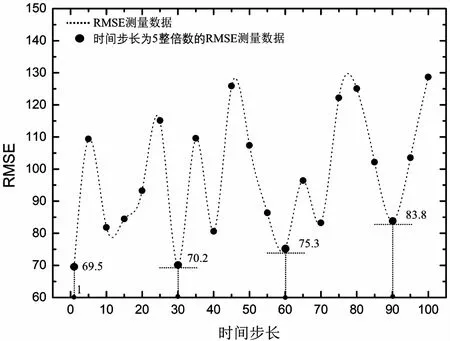
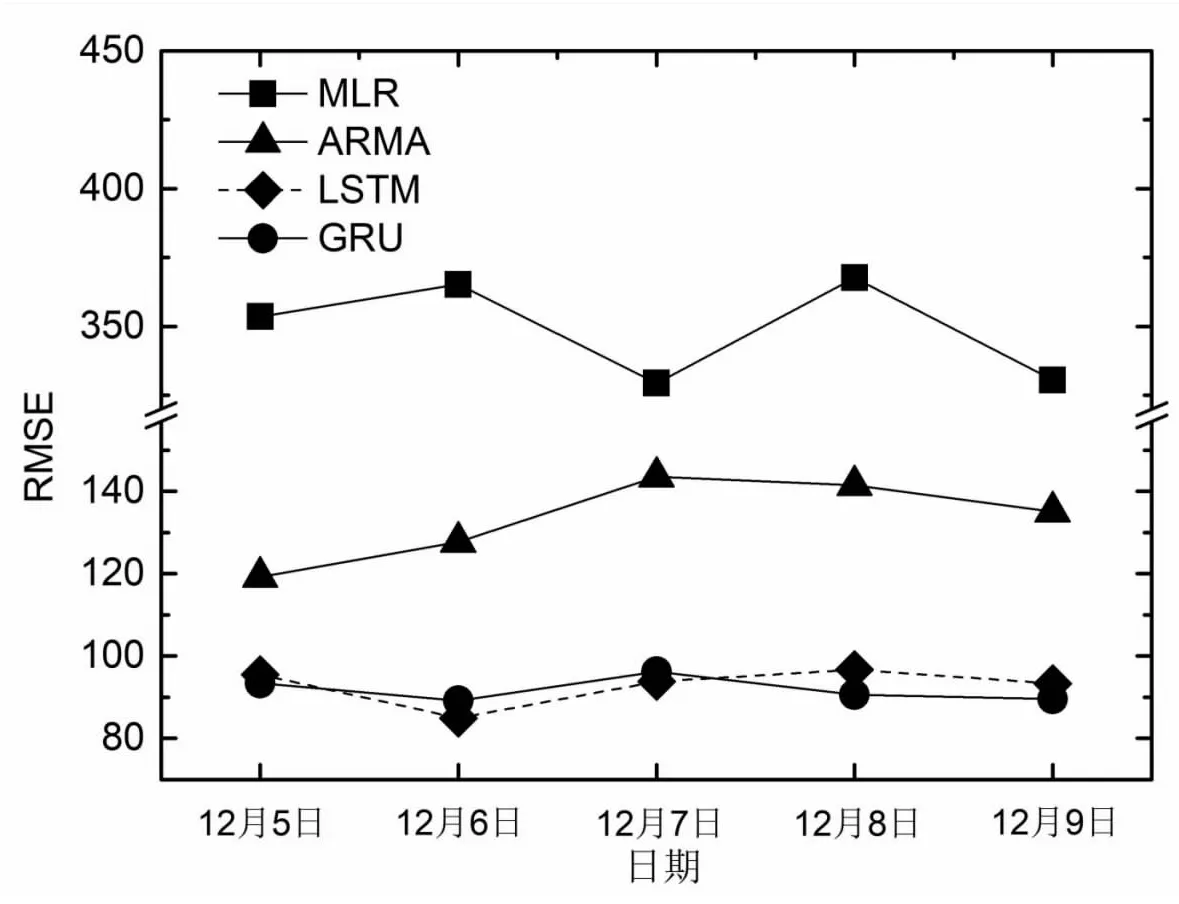
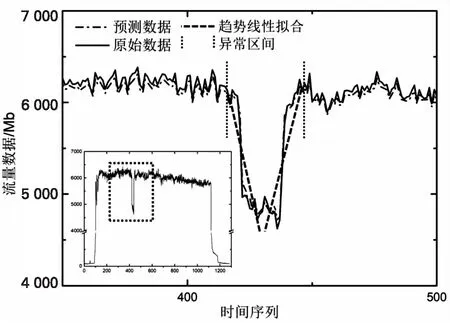
Step1 处理样本集：假设经过小波前置分析后得到近似信号的时间序列为F={f1,f2,…,fn}，那么可以将该序列划分为GRU模型训练集与测试集，分别用Ftr={f1,f2,…,fv}，Fte={fv+1,fv+2,…,fn}表示，其中v

Step2 设定GRU参数进行训练：通过设定时间步长L对序列进行窗口分割，分割后模型输入为X={X1,X2,…,Xv-L}，Xq={fq',fq'+1,…,fv-L+q'}。该输入经过隐藏层后形成的输出为P={P1,P2,…,Pv-L}，对应的理论输出为Y={Y1,Y2,…,YL}。选择公式(6)损失函数最小化作为优化目标，遍历学习率及训练步数范围，使用adam作为优化算法不断更新网络权重，得到在训练集范围及相关参数范围内最优神经网络。

(6)

3.2 数据拟合准确度选择

平均绝对误差mean absolute error (MAE)、平均绝对百分误差mean absolute percentage error (MAPE)和均方根误差root mean square error (RMSE)是最常用的数据拟合准确度预测评价指标。MAE主要用于测量实验数据集的预测值与实际值之间的平均绝对误差。MAE定义为：

(7)

MAPE主要用于测量拟合数据与真实数据的百分比误差，MAPE数学定义为：

(8)

RMSE主要用于衡量拟合数据与真实数据的均方根差，RMSE数学定义为：

(9)

式(7)、(8)、(9)中，a(t)表示第t个时间序列真实数据，f(t)表示第t个时间序列拟合数据，n为时间序列总数。从数理角度分析，MAE和MAPE在数学形式上都属于L1范数，而RMSE在数学形式上属于L2范数，数学表达式的幂级数约高，那么这个表达式的输出结果则对异常值越敏感。这也代表当拟合数据集合中出现一个异常大或异常小的数据值时，RMSE的计算结果将比MAE和MAPE大。假设有如下两个数据集合：

set1=[5,10,5,10,5,10,5,10,5,10, 5,10,5,10,5,10,10]

set2=[5,10,5,10,5,10,5,10,5,10,5,10,5,10,5,10,1 000]

集合set1和set2的区别为末尾数据分别是10和1 000，集合set2的末尾数据1 000可以看作为拟合数据的异常大值。将set1集合作为真实数据，set2集合作为拟合数据，由此计算MAE为58.2，RMSE为240.1，MAPE作为MAE的数学变换，敏感幅度低于MAE。由此可证明，对于时间序列拟合结果的异常值，RMSE比MAE和MAPE更加敏感，因此选择RMSE作为拟合准确度的定义表达。

图4 流量数据与拟合结果对比

对2017年7月10日流量数据进行GRU拟合，GRU优化算法为adam函数，时间步长为30，学习率η=0.05。使用7月8、9日两天数据作为训练集，拟合结果与测试集数据对比如图4所示，数据拟合准确度定义为RMSE，拟合结果与测试集数据基本一致，拟合准确度的值为88.23。

3.3 不同时间步长拟合结果对比及趋势预测

GRU模型中的时间步长L决定了在流量数据拟合中使用L个序列来预测第L+1个序列值。图5展示了L为1至100时，GRU模型对2017年8月8日流量数据的拟合准确度变化，黑色标点代表L为5的整倍数拟合均方根误差，当L分别为1、30、60、90时均方根误差处于局部极小，该结果证明GRU在解析流量数据过程中，对1分钟、30分钟、60分钟以及90分钟内流量数据间依赖敏感，验证了由铁路整点或半点售票时刻规则所决定的数据结构特性适于使用GRU算法解析。

流量数据趋势预测也是异常预警的常用手段，文中采取的趋势预测基于GRU算法拟合数据。假设拟合数据长度为L，通过设定窗口大小U，滚动遍历L，并且对窗口范围内拟合数据P使用最小二乘法得到线性拟合，P={Pn+1,Pn+2,…,Pn+U}，n∈(1,L-U)。

图5 不同时间步长RMSE拟合统计

对2018年6月18日去除服务开启与关闭时刻前后的流量数据进行GRU分析，如图6所示，在GRU拟合结果的基础上，实施滑动窗口大小为100的趋势预测，其他任意的窗口大小的预测趋势都与拟合结果基本吻合。

图6 流量数据趋势预测

4 算法验证

4.1 对比模型

为了验证GRU算法的有效性，文中将GRU算法与以下3种时间序列预测模型进行对比。

(1)多元线性回归。

多元线性回归MLR是传统的统计学方法用于对多变量、多影响因素进行分析从而实现预测[15]。该模型函数如下：

yt=a0+a1yt-1+a2yt-2+…+akyt-k+b

(10)

其中，yt为t时序点预测目标，yt-1,yt-2,…,yt-k为t时刻前k个历史数据，a为模型系数，b为固定偏差。多元线性回归将不同时刻的历史数据作为不同的自变量，k也称为数据窗口长度，在对比模型中选取k与测试集样本个数相同。

(2)自回归移动平均。

ARIMA差分整合移动平均回归模型是自回归模型的经典算法，利用历史时序数据对当前时刻进行预测，模型本身采用不同时刻数据差分的原理解决对样本数据平稳性要求高的问题[16]。该模型函数可用ARIMA(p,d,q)表示，p,d,q分别为自回归项数、差分阶数及移动平均项数。差分1阶或2阶即可满足模型需求，p,q需要自相关函数及偏自相关函数来确定。

(3)LSTM长短时记忆神经网络模型。

LSTM长短时记忆神经网络模型利用“遗忘门”结构实现了序列数据间依赖解析，并通过遗忘门决定历史时刻状态信息保留至当前状态的信息量大小[17-18]。GRU作为LSTM神经网络模型的改进，在保证高拟合精度的情况下，降低了模型训练耗时。文中使用相同时间步长及训练批次对LSTM与GRU算法进行对比。

4.2 对比结果

使用以上四种算法分别对2017年12月5日至12月9日5天流量数据进行拟合，10月23日至10月27日流量数据作为训练集。文中所有计算结果使用计算机的配置相同:处理器为Intel i5-7300；内存为8 GB；显卡为GTX 1050Ti；操作系统为Windows 10( 64位)；实现计算机开发环境为PyCharm 2018.2.4；实现语言为Python 3.6.9；程序开发GRU框架使用Python Tensorflow程序包。图7为5天流量数据拟合准确度变化，GRU的平均拟合准确度最优91.8，虽然LSTM拟合准确度与GRU接近，但是在时间步长与训练批次相同的训练过程中，GRU耗时相对于LSTM具备极大优势。

图7 多种算法拟合对比统计

表1 算法拟合对比RMSE数值统计

4.3 异常数据检测

为了进一步验证GRU在铁路客票业务中异常预警的可行性，选取了2018年1月7日、2月11日的流量数据进行验证，该2日内的流量数据分别在当天有大范围波动，与实际部分业务故障相符。选取以上测试集前2天流量数据作为训练集样本，故障点附近范围的趋势预测及流量数据拟合结果如图8所示。两日流量数据拟合RMSE分别为114.5和99.3，GRU拟合结果与实际流量数据的近似且线性趋势预测的准确。

(a)1月7日流量数据

(b)2月11日流量数据

5 结束语

文中提出了基于GRU神经网络的流量数据时间序列预测方法，不同时间步长的拟合结果与铁路售票规则形成的数据依赖规律相一致，体现了GRU在长跨度客票业务流量数据依赖解析方面的优势。通过3种不同时间序列预测模型与GRU流量数据拟合对比，GRU的最优拟合准确度证明了该算法具备较高的准确性。经过GRU对异常流量数据分析，在故障点处的拟合近似以及趋势预测准确，使得预测差值与趋势线性拟合斜率具备成为铁路客票业务流量数据预警监控指标的可能。