基于梯度优化的多任务混合学习方法

郭 辉，郭静纯，张 甜

(宁夏大学 信息工程学院，宁夏 银川 750021)

0 引 言

传统的机器学习、深度学习方法通常将注意力集中在单个任务上，在部分领域甚至能取得超越人类行为的优异性能；但却无法做到像人类一样，利用不同任务之间的关联信息，触类旁通地掌握更多的知识技能。或者说，通过共享相关任务之间的表征，可以使模型更好地概括原始任务，这被称为多任务学习。它是一种模仿人类泛化能力的方法，让多个相关任务并行学习，在学习过程中，每个任务都会提供属于自己特定领域但同时也有助于学习其他任务的信息，这可以有效提高网络的泛化能力。因此，多任务学习方法的关键是在所有任务的联合假设空间中引入归纳偏置，这种归纳偏置反映了网络对任务相关性结构的先验认知[1]。如何更好地利用网络结构实现共享是目前多任务学习面临的主要挑战之一[2]。

作为多任务学习最常用的一种深度神经网络结构，硬参数共享通过让多个任务共享一些隐藏层来学习任务之间的联合表示，而在输出端根据每个任务的不同特性划分出各自的分类器预测输出层[3]。硬参数共享神经网络在设计共享层结构时，不需要对任务之间的关系进行精确建模，这虽然简化了网络结构设计，但是也导致网络在训练的过程中无法根据任务的实际相关性调节共享量。此外，每个任务的分类器预测输出层是相互独立的，这会阻断共享信息在该层的自适应传播，因此网络也无法利用输出层建立任务之间的相关关系。当任务之间联系不紧密时，这种结构会增加负迁移的风险；而且Yosinski J等学者指出，即使任务之间联系紧密，负迁移的现象也会随着网络层数的增加而愈加明显[4]。由此可知，硬参数共享神经网络的结构设计虽然简单，但是只能建立在任务具有较高相关性约束条件的基础上。

为了解决硬参数共享机制存在的问题，文献[5-7]提出了不指定共享结构的软参数共享。该方法为每个任务设计了同样的网络结构，在各层上通过范数约束表征任务的相似性，并取得了较好的结果。但是，随着任务数量的增加，软参数共享网络结构和参数都会变得非常复杂；而且，与硬参数共享神经网络一样，它也无法根据任务的实际相关性调节共享层的共享量，以及对任务的分类器预测输出层进行关系建模。

在上述参数共享机制研究的基础上，为了实现对输出分类层的关系建模，文献[8]提出了一种可以加强各个任务分类层之间联系的深度关系网络。该网络在全连接层和分类层之间额外增加了用于描述多个任务之间相关关系的全连接层；并通过引入张量正态分布学习网络深层的共享特征以及任务之间的相关关系[9]，从而避免了硬参数共享和软参数共享在共享层和分类层之间引起的负迁移现象。但是，张量的引入仍然建立在假定大多数任务之间存在整体相似度的基础上[10]，因此这并没有从根本上解决硬参数共享的问题。

在这之后，文献[11-13]开始尝试拆分任务之间的共享特征和各自特定特征，并调节共享层的共享量。据此先后设计了拆分缝合网络、水闸网络、自适应层分堆网络等结构。其中，拆分缝合网络和水闸网络是自适应层连接的两种表现形式。拆分缝合网络通过多个任务对应层之间的连接单元控制特征参数信息的传递。在此基础上，水闸网络进一步扩展了这种结构，在每个任务网络输出的末端整合了所有的连接单元，从而完整地描述了各个网络层之间可能的信息传递。自适应层分堆网络是一种没有连接单元的学习方法，自顶向下逐层扩展，自动寻求各层之间可能的参数共享结构。上述三种方法都是依据各个任务在每层特征网络上共享信息与特定信息的不同逐层改变网络结构。虽然它们在一定程度上缓解了任务高相似度的约束，但是结构复杂，学习形式由一般的层参数共享演变到具体层之间的连接和切换，从简单的整体相似性建模演变到共享和私有特征子空间的划分[10,14]，使其失去了硬参数共享网络结构的简洁性。

多任务学习网络通常采用交替训练和联合训练两种训练方式，如图1所示。当所有任务的训练集相互独立时，网络采用交替训练：先在输入层为不同任务输入各自的训练样本，然后交替收敛每个任务的损失函数；这就要求每个任务的训练样本数量基本均衡，否则网络会偏向数据量较大的任务。当所有任务共用一个带有不同标签的训练集时，网络采用联合训练：在输出层将每个任务的损失函数相加，让所有任务共用一个优化函数进行训练；在这种训练方式下，网络需要合理地进行损失函数加权，使得所有任务的学习具有同等作用。

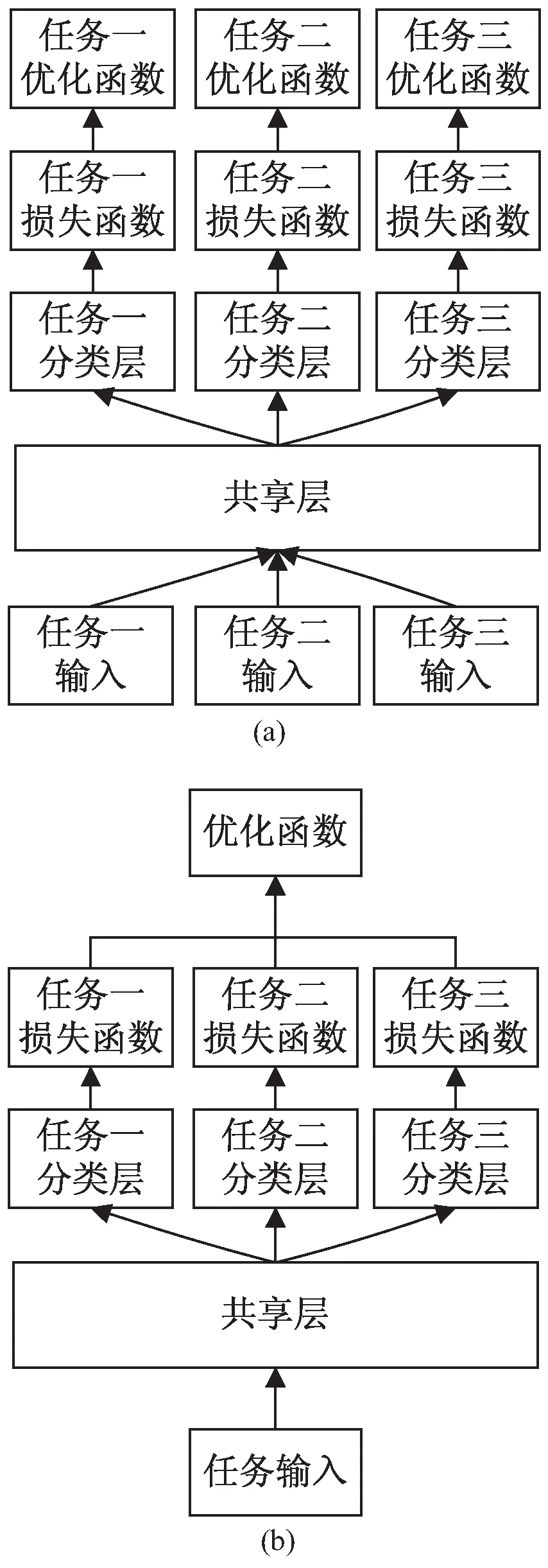
图1 交替训练(a)与联合训练(b)

这两种训练方式都需要网络将不同任务区分开，并给每个任务设定各自的损失函数。但由于目前对任务的相似性、关系、层次性等的理解非常有限，使得区分任务并不是一件能轻松完成的事情[15]；而且，即使实现了任务的区分与各自损失函数的设定，这仍然会出现让网络在所有任务的联合假设空间中偏向某个任务的问题，进而导致网络参数无法对全部任务等效收敛。

针对上述问题，提出了无需进行任务区分、不同任务数据一同参与的混合训练方法；并结合不同层次特征作用的差异，基于深层特征梯度变化进一步优化网络参数，提升网络性能，并保持了硬参数共享网络结构的简洁性。通过在UCI公开数据集中鸢尾花和天平秤数据上的实际应用，以及与传统的硬参数共享神经网络的纵向对比，验证了基于梯度优化的多任务混合学习方法的有效性。

1 多任务混合学习方法

多任务混合学习方法具体实现过程可以分为混合训练与梯度优化两个步骤，如图2所示。首先进行混合训练，根据多任务混合数据依次训练调节共享层到各个特定任务分支层的网络参数；其次进行梯度优化，根据不同任务在共享层梯度变化的不同优化该层网络参数，加快网络训练速度。

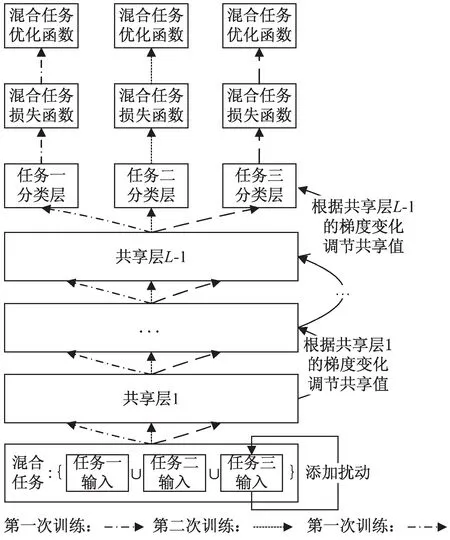
图2 多任务混合学习方法

1.1 混合训练

设硬参数共享神经网络从输入层l=0、共享层l=1,…,L-1到输出层l=L，共L+1层，Wl表示每层的连接权参数矩阵，bl表示每层的偏置或阈值，其中l=0,1,…,L。

若每个任务的训练数据集为Zn={(xni,yni)}，其中n=1,2,…,N，表示二分类任务的种类数，i=1,2,…,S，表示每类任务的正样本和负样本数，则由N个二分类问题组成的多任务训练数据集为Z=Z1∪Z2∪…∪Zn。对于第n个任务而言，所有属于这个任务的样本为正样本，而其他样本则为负样本。通过混合训练，实现将第n个任务的样本从其他任务类型中正确地分离出来。为了避免区分不同任务的难题，在随机初始化网络参数之后，可以将N个任务的数据无差别地混合在一起，即训练数据集Z。将训练数据集Z通过输入层W0直接送入硬参数共享神经网络中进行训练。输入数据在神经网络的前向传播过程中，若每层激活值为al,l=0,1,…,L，则其计算公式如下：

al=g(WlTal-1+bl)

(1)

其中,g(·)是激活函数。

多个任务进行混合训练时，网络可以将它们看作一个任务进行学习，因此，无需为每个任务设定各自的损失函数。则此时的多任务混合学习网络的损失函数计算公式为:

L(aL,y)=-(ylog(aL)+(1-y)log(1-aL))

(2)

其中，y表示混合任务的期望误差。

在混合训练过程中，基于训练数据Z在网络的共享层与第一个分支输出层的反向误差传播调节相应的网络参数，当第一个分支网络输出的损失函数L(aL,y)收敛到最小值时，结束本次网络训练；并把此分支输出层设定为第一个任务的特定分类层，同时将此时共享层的网络参数作为第二次训练，即从共享层到第二个分支输出层网络结构中共享层的初始化参数，而第二个分支输出层仍为随机初始化参数。采用同样的训练调节策略，当第二个分支网络输出的损失函数收敛到最小值时，结束第二次网络训练。此时，第二个分支输出层设定为第二个任务的特定分类层，同样将共享层参数作为第三次训练中相应网络部分的初始化参数。依次类推展开后续网络训练，直至所有任务在特定分类层上收敛到最小值时，混合训练结束。该网络混合训练算法流程总结如下：

算法1：混合训练。

输入：多任务混合训练数据集Z与相关参数(迭代次数Total，学习速率α，损失函数收敛阈值β)

输出：N个任务的分类性能

1.硬参数共享网络参数θ随机初始化

2.for episode←1 to Total do//迭代

3.单个分支输出层(即特定任务分类层)上计算相应的混合任务损失误差

4.if前后两次混合损失误差<βthen 收敛，且

N←N-1

5.else then返回步骤3

6.end if

7.ifN≠0 then当前共享层参数作为下一次训练共享层的初始化参数，返回步骤2

8.else

9.end if

10.end for

由上述混合训练流程可知，它在输入端混合了所有任务的训练集，并依次在每个任务的特定分类层上收敛混合任务的损失函数，从而避免了区分任务的难题。与此同时，所有任务共用一个损失函数可以平衡每个任务的训练，并通过前一次训练的共享层参数作为后一次训练的共享层初始化参数，可以让全部任务的分类性能在损失函数误差收敛的过程中逐渐趋于优化。

1.2 梯度优化

通过前面的混合训练可以得到较好的网络参数，但由于在此训练过程中任务与参数之间的相互协调，使得对特征提取和任务分类影响非常显著的部分关键参数并未达到最优值，为此需要进一步调整与优化。将硬参数共享神经网络的每一个学习任务的训练样本作为自变量，共享层梯度变化作为因变量，根据影响因子权重分析方法，定量评价各个自变量对于因变量影响的重要性程度差异：当训练样本数据变化相同幅度时，共享层每一列梯度变化越大，则表明该列梯度在特征提取中越重要，也是影响任务分类性能的关键，据此选出需要进一步调节的相关重要参数。而且，从网络训练速度的角度来看，当这部分网络参数对应的梯度值相对最优值过大时，表明训练速度过快；反之，则训练速度过慢。在反向传播过程中的梯度值过大或过小时，都需要对相应的网络参数进行惩罚，只有当它们以近似的速度进行训练时，才能使得网络训练达到整体均衡或最优[16]。

基于BP算法，网络输出层的反向传播过程可表示为：

(3)

(4)

(5)

对网络共享层第l=L-1层，当输出层向该层反向传播时，其梯度计算公式为：

(6)

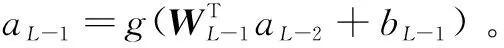
梯度优化的主要操作步骤如下：首先，根据数据集Z混合训练的网络参数和超参数，提取每个共享层的相应梯度Δl,l=1,2,…,L-1；其次，按照影响因子权重分析方法，依次将每个任务的每个特征增加或减少自身数值的10%～20%，据此得到新数据集Z'进行混合训练，进而提取每个共享层相应的梯度(Δl)'；再次，根据梯度Δl与(Δl)'计算两者的差值矩阵(Δg)l，其中行为样本个数，列为该层神经元个数，表示随着训练样本特征值的变化每个网络共享层的梯度变化大小；最后，按列计算每个任务的共享层梯度变化均值，并依据其绝对值大小排序，依次调节每个任务在各个共享层上梯度变化最大的所对应位置的激活值，即该层激活值点乘调节系数矩阵[δn1,δn2,…,δnq]l，实现网络参数的进一步优化，提升所有任务的分类性能。其中n表示任务编号，q表示列数，l(l=1,2,…,L-1)表示共享层数。

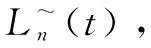
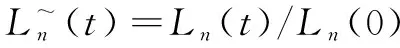
(7)

其中，n=1,2,…,N。它可以衡量影响任务分类性能的关键参数的训练速度：损失率越低，则训练速度越快；反之则越慢。

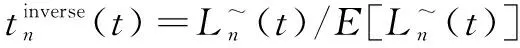
(8)

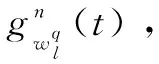
(9)

(10)

根据上式调节系数矩阵δ。

由深度学习神经网络的学习过程可知，靠近输入层一侧的浅层网络通常提取局部、具体的一般特征，而随着网络层数的增加，深层网络提取全局、抽象的本质特征[17]。并且，与前者的浅层特征相比，后者的深层特征对于任务分类的作用更重要。据此，可以简化网络梯度优化过程，只调节共享层部分最后一层神经元梯度变化最大所对应的激活值，加强深层特征的关键作用，从而进一步提升网络整体性能。与此同时，这种有针对性地忽略浅层特征、关注深层特征的简化处理方法，不仅有助于保持硬参数共享网络结构的简洁性特点；而且在一定程度上可以有效解决多任务学习中的非平衡问题，即在误差反向传播训练过程中，如果数据集中某个任务占据主导地位，必然会通过诱导具有较大的梯度来表达这种主导地位，从而使得整个网络具有某种任务的偏好，导致其余任务的分类性能无法达到整体最优[17]。因为它是根据每个任务在共享层的最大梯度变化所在位置调节相应的激活值大小，所以具有明确的指向性，可以避免训练数据集中任务数量不均衡所带来的影响。

在第一步混合训练的基础上，根据梯度变化不同与层次特征作用差异进行第二步梯度优化，其处理过程总结为算法2，如下所示：

算法2：梯度优化。

输入：多任务混合训练数据集Z与相关参数(迭代次数Total，学习速率α，损失函数收敛阈值β)

输出 ：N个任务的分类性能

1.基于训练数据集Z，按照算法1进行混合训练，计算此时各个共享层的梯度Δl(l=1,2,…,L-1)

2.选取某个任务，逐一增加或减少训练样本特征值的10%～20%，生成新的训练数据集Z'，同样按照算法1计算相应的各个共享层的梯度(Δl)'

3.计算梯度变化(Δg)l

4.if未改变所有任务训练样本的特征值 then返回步骤2

5.else then//已改变所有任务训练样本的特征值

6.end if

7.根据改变每个任务训练样本特征值后的梯度变化，依次调节每个任务在各个共享层上梯度变化最大的一列对应位置的激活值

8.测试网络分类性能，if 所有任务分类准确度提高 then 结束

9.else then//任务分类准确度没有全部提高

10.返回步骤7

11.end if

2 实验研究

为了检验基于梯度优化的多任务混合学习方法的实际效果，选取UCI公开数据集中的鸢尾花和天平秤数据为对象，进行具体的应用实验。

2.1 实验设置

实验数据中的鸢尾花数据分为三类，依次为Setosa、Versicolor和Virginica；每类共有50个正样本，包含叶瓣长度、叶瓣宽度、花瓣长度和花瓣宽度四个特征。而其余的天平秤数据也包含四个特征，分别是左权重、左距离、右权重以及右距离。通过比较左右两边的权重与距离的乘积，可以将这部分数据集分为天平秤平衡、天平秤偏左和天平秤偏右三类。其中天平秤平衡类共有49个正样本，其余两类都有288个正样本。

根据上述两个公开数据集的实际情况，文中新建了三个任务进行实验。第一个任务是判断天平秤是否偏向左边，第二个任务是判断天平秤是否偏向右边，而第三个任务是判断鸢尾花是否属于Versicolor或Virginica。每个任务的样本总数为150个，按7∶3的比例随机初始化各个任务的训练集和测试集。

文中采用的硬参数共享神经网络共四层，即一个输入层、两个共享层和一个特定任务分类输出层。其中两个共享层的神经元个数分别为4和5，且每层选用的激活函数都为Sigmoid函数。

2.2 实验结果与分析

将设定的三个任务的混合训练集通过输入层送入该神经网络进行基于梯度优化的多任务混合学习实验。

实验结果发现，当依次改变任务一、任务二和任务三的训练样本的特征值时，相应地对最后一个共享层的第二列、第一列和第三列的梯度影响最大。这表明不同任务在最后共享层的关键特征响应不同。因此，对于任务一，可令第二列的激活值乘上一个调节系数，则任务一的准确率会随着调节系数的增大而提高。需要注意的是，调节系数存在一个上限，一旦超过这个上限，任务一的准确率在达到最高值后下降。当δ12=3时，任务一的准确率能达到98%。同样，当δ21=2.3时，任务二的准确率可以达到99%；当δ33=2.4时，任务三的准确率也能达到99%。而任务特征值的改变对其余列的梯度变化影响相对不大，为简化处理，可以无需调节这部分激活函数。

在硬参数共享多任务学习网络中，当一个任务的准确率显著提高时，由于任务之间的密切相关性和网络自身结构的约束，其余任务的准确率通常会下降。因此，在不降低任何一个任务准确率的前提下，采用基于梯度优化的多任务混合学习方法所得到的多任务学习神经网络，其在测试集上的实验结果如表1所示。

表1 多任务混合学习测试结果

为了与传统训练方法对比，可以将上述三个任务的数据集分别送入同样的硬参数共享多任务学习神经网络中，按照交替训练方法调节网络参数，与文中提出的混合学习方法在测试集上进行实验对比，结果如表2所示。

表2 传统交替训练学习与混合学习测试结果对比

除此之外，在传统的硬参数共享神经网络训练结果中，也可以根据特征层次差异与梯度变化不同进一步优化网络参数。优化前后的实验对比结果如表3所示。梯度优化后，在任务三准确率保持不变的基础上，准确率最低的任务一从47%提升到69%。由于任务之间的密切相关性和网络自身结构的约束，任务二的准确率只下降了0.01。梯度优化后的整体效果较好。

表3 交替训练后是否梯度优化参数实验结果对比

3 结束语

文中提出的基于梯度优化的多任务混合学习方法，首先通过混合多任务训练数据、一同送入网络进行学习，避免了硬参数共享网络训练过程中需要区分不同任务的难题；其次，根据共享层部分深层网络所提取的全局本质特征对于后续分类任务更重要的特点，以及响应任务变化的梯度变化量不同，在保持硬参数共享网络结构简洁性的基础上，有针对性地优化共享层网络参数，提升网络整体性能，同时还不受训练数据集中任务不均衡的影响，在一定程度上有效解决了硬参数共享网络在训练过程中的非平衡问题。而且，该方法也可应用于其他的多任务学习方法中。最后，通过在UCI公开数据集中鸢尾花和天平秤样本上的应用实验，验证了该方法的有效性。

基于梯度优化的多任务混合学习方法在应用过程中，如果不同类型的任务之间差别非常显著、关联较少，且某些任务的训练数据严重不足，会对硬参数共享多任务学习提出严峻挑战，这些还有待后续研究工作的持续改进与完善。