分布式抗干扰时间协同制导律的研究

朱豪坤，鱼小军，罗艳伟，刘 闯，张 婷

(湖南云箭集团有限公司，长沙 410100)

0 引言

为了实现协同突防、饱和打击，多弹同时弹着制导律在近几年得到了广泛的研究[1-12]，根据飞行过程中各弹是否进行数据交互将同时弹着制导律分为时间控制制导律[1-4]和时间协同制导律[5-12]。相对时间控制制导律，时间协同制导律发射前无需装订指定弹着时间，弹群在数据链的支持下，通过协同实现同时弹着，属于整体闭环控制。在时间协同制导律中，若参与作战的导弹需要接收弹群中所有导弹的数据才能实现同时着靶，则称为集中式强连接协同，若导弹只需部分导弹的数据即可实现协同，则称为分布式弱连接协同。在工程实践中，分布式弱连接协同方法具有更高的研究价值。

目前研究中，赵世钰等提出了一种基于协同变量的双层结构时间协同制导律[5-6]，实现了多弹基于通讯网络的时间协同控制；王青等考虑存在通信时间延迟和通讯网络不确定性问题，设计了一种分布式时间协同制导律[7]；张友安等基于领弹-从弹策略，通过动态逆控制方法，提出了一种多弹协同时间控制制导律，实现了领弹-从弹策略在多弹协同[8]的应用；Zhang等通过用矩阵图论的形式表示通讯网络拓扑，考虑复杂战场情况下引起的通讯不稳定对弹群协同的影响，提出了一种通讯拓扑时变的时间协同制导律，实现了分布式结构的多弹协同同时着靶[9]；邹丽等考虑多异构导弹的协同问题，提出了一种分布式协同制导方法，实现了异构多导弹的协同问题[10]。

然而，面对复杂的战场环境，弹群受到敌方反导系统的干扰时，部分导弹会因干扰而无法正常工作，使协同制导变得更加困难。现有文献中很少考虑到弹群中某些导弹受扰后无法正常工作的抗干扰问题。针对该问题，在时间协同制导律的基础上集成在线滤波算法，提出了一种分布式抗干扰时间协同制导律，在弹群中某些导弹受到干扰时，将受扰导弹数据从协同网络数据链中滤除，使正常弹群依然能够在制导律的导引下实现同时着靶。

1 问题描述

如图1所示协同制导示意图，在二维平面中，考虑n枚导弹协同攻击同一目标的场景，导弹之间通过通讯网络进行数据交互，各枚导弹实时获取导弹群中附近导弹的状态信息，同时对弹着时间进行协商与控制。

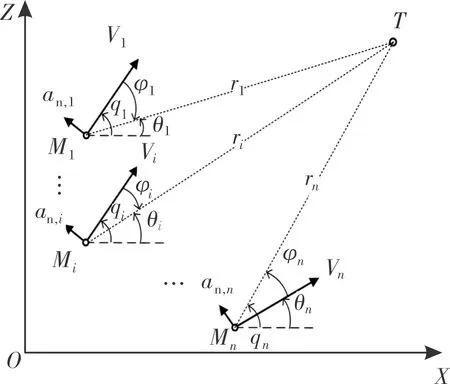
图1 协同制导示意图

设Ω={1,2，…,n}为参加饱和打击的导弹索引编号的集合，则对于第i(i∈Ω)枚导弹，ri,qi,φi,θi分别为第i枚导弹的弹目相对运动距离、视线角、视场角、飞行前置角；Vi为第i枚导弹的速度模值，在作战中假设恒为定值，但各枚导弹的速度不一定相同；an,i为第i枚导弹的法向加速度模值，即系统中的控制输入指令，始终与导弹的速度方向垂直。可以得出该系统的二维平面数学模型为：

(1)

其中i=1,2，…,n。

假定弹群均使用比例导引法作为制导律：

(2)

式中N为制导比例系数，第i枚导弹的剩余飞行时间可以近似表示为[4]：

(3)

在此基础上，进一步考虑如图2 所示的抗干扰时间协同制导问题。弹群集合Ω={1,2，…,n}由正常导弹子集N={i=1,2,…,m}(m≤n)和受扰导弹子集F={i=1,2,…,f}(f≤n)构成，有Ω=N∪F。受扰导弹的数量最多为f个。在实现中，f可以根据通讯网络的可靠性、导弹的抗干扰能力、制导律的鲁棒性等因素来确定，只要弹群的相关方案确定了，就可以计算出f的具体数值。

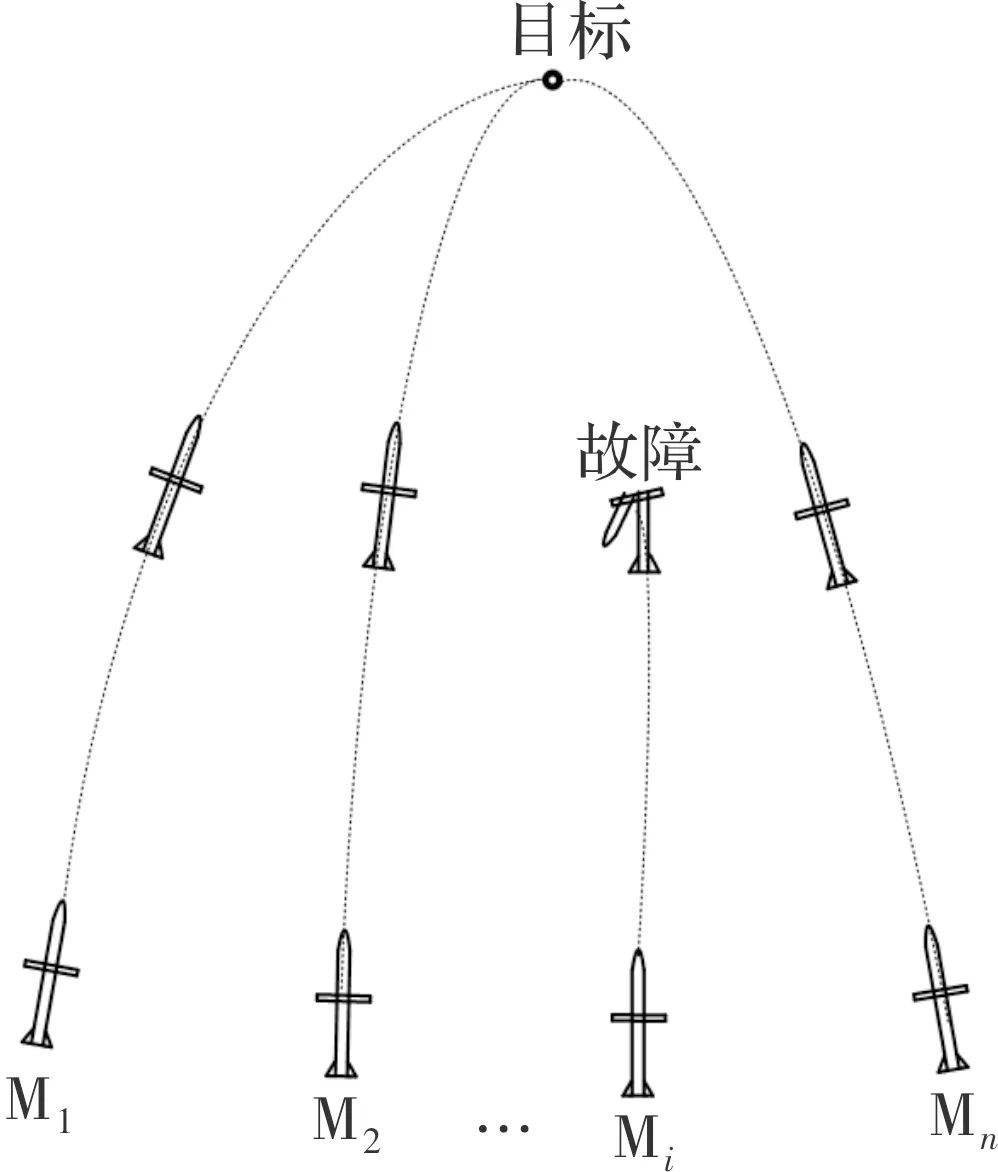
图2 抗干扰协同制导

以矩阵的形式来描述通讯关系，参与作战的导弹的集合定义为Λ={1,2,…,n}，则相应的通讯矩阵定义为A=[eij]∈R(n-1)×(n-1)，如果第i枚导弹能够从第j枚导弹中获取数据，则称第j枚导弹为第i枚导弹的内邻，eij=1，否则eij=0，第i枚导弹的所有内邻可以用集合Ii={j∈Ii∶eij=1}表示，Ii为第i枚导弹的实时内邻子集。如果第j枚导弹可以从第i枚导弹中获得数据，则称第j枚导弹为第i枚导弹的外邻，第i枚导弹的所有外邻集合为Oi。

综上，文中还需作出以下两点假设：

1)假设最大受扰导弹数f是已知的；

2)假设导弹受扰后每次通讯给其所有外邻发送同样的数据(也即各外邻导弹从受扰导弹收到的数据是恒定不变的)。

2 分布式抗干扰时间协同制导律的设计

考虑导弹组网的灵活性，基于时间协同制导律集成滤波器的思路，来解决多弹分布式抗干扰时间协同制导问题。通过滤波器滤除受扰导弹数据，然后将滤波后的数据进行协同制导，设计的分布式抗干扰时间协同制导律为：

(4)

其中ξi为第i枚导弹滤波后的协同制导时间，具体如(5)式所示：

(5)

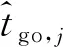
(6)

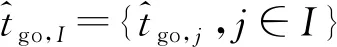
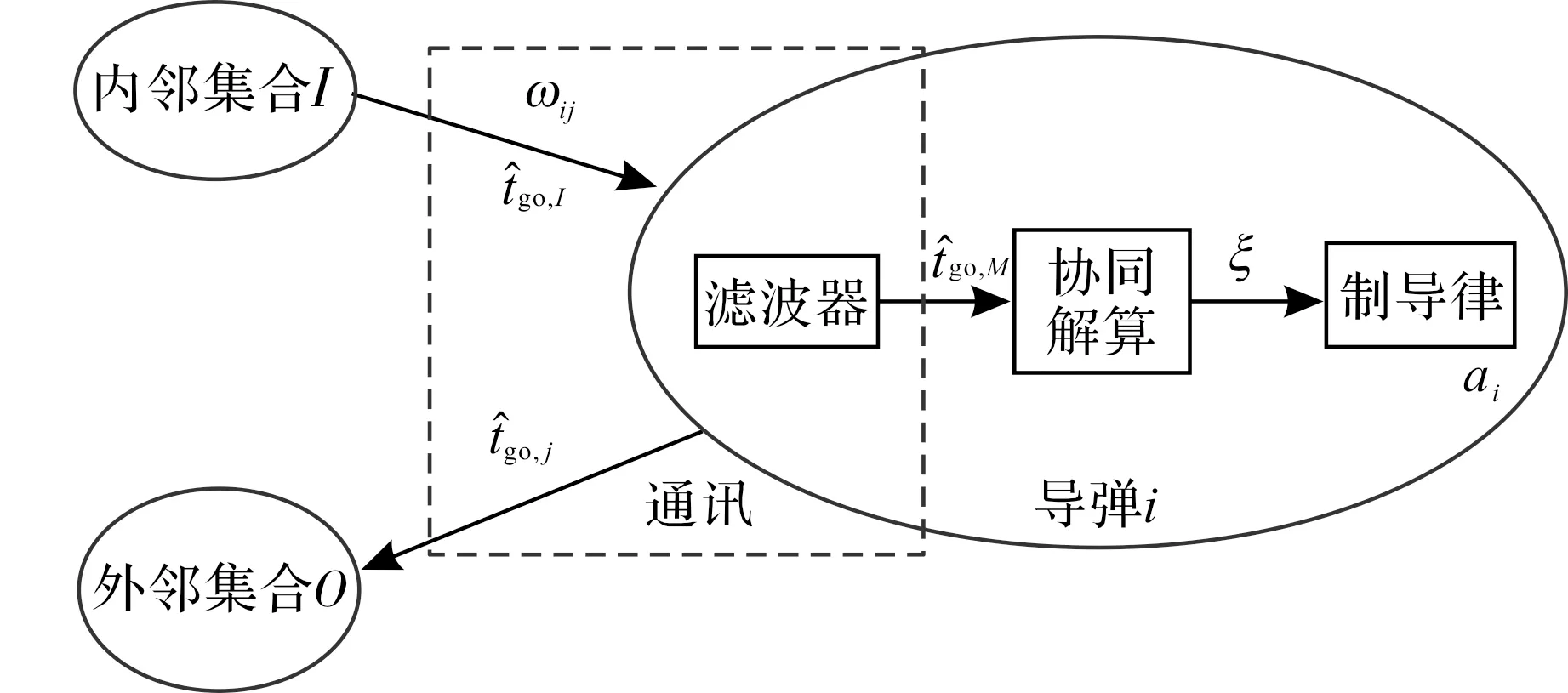
图3 制导结构

下面对该抗干扰性时间协同制导律的实施步骤进行阐述，从第i枚导弹的视角进行分析：

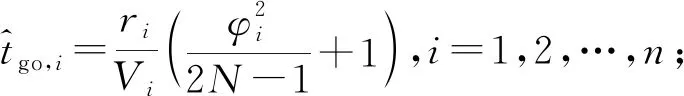
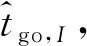
3)第i枚导弹将收到的所有剩余飞行时间按从小到大排列成一个数列；

4)如果有不超过f个收到的剩余飞行时间估计值大于第i枚导弹自身的剩余飞行时间估计值,则第i枚导弹丢弃所有大于其剩余飞行时间估计值的数据,否则第i枚导弹丢弃f个大于其剩余飞行时间估计值的数据;

5)按照式(5)解算调整时间ξi；

6)按照式(4)解算控制指令an,i。

在每个解算周期，第i枚导弹与其相邻导弹通信，同时计算自身剩余飞行时间，并根据算法规则滤除故障导弹的剩余飞行时间估计数据，再进入下一步协同解算与制导指令生成。

3 仿真验证

为验证所设计的分布式抗干扰时间协同制导律的可行性及其性能，通过协同作战算例对该制导律进行仿真验证。算例使用5枚导弹对位于坐标原点的目标进行协同打击，弹群采用如图4所示分布式通讯网络拓扑，其中单向箭头表示数据只能单向传输，双向箭头表示数据可以在两弹之间双向传输。参与协同作战的各弹的相关飞行参数如表1所示。

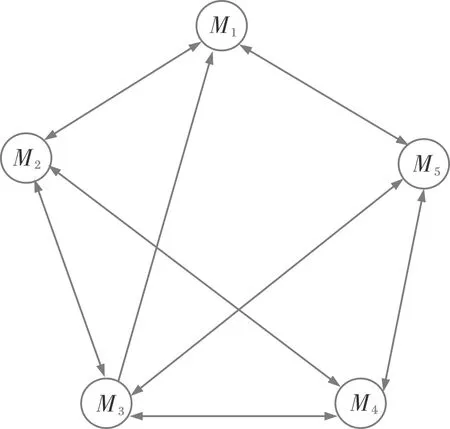
图4 通讯网络拓扑

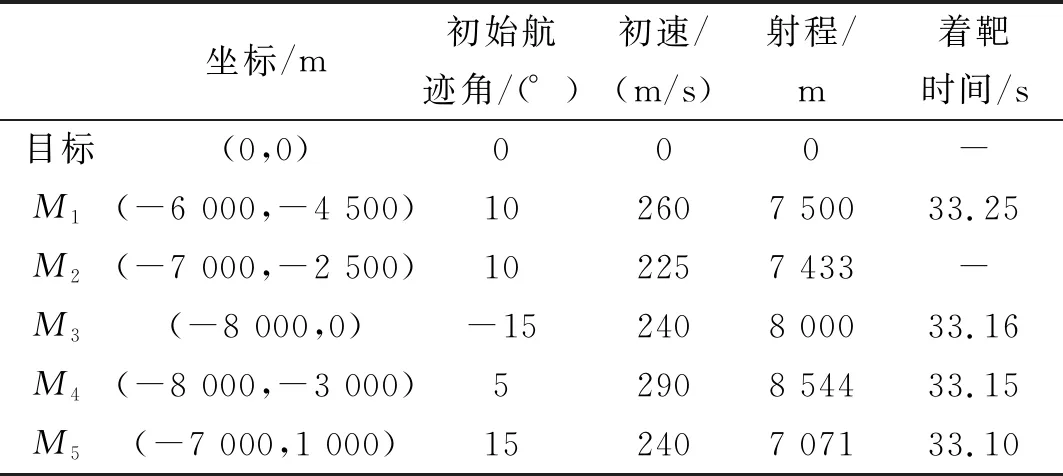
表1 协同作战导弹参数

5枚导弹组成协同作战弹群，其制导律参数设定为：k1=k2=…=k5=-0.2，N=3，导弹重力加速度g=9.8 m/s2，最大可用过载amax=5g，导弹2(M2)为故障导弹，设定其在仿真开始后的第3 s发生故障，弹群中最大故障导弹数目f=1。目标静止，仿真步长设定为0.05 s，当弹目距离小于3 m时结束仿真。仿真结果如图5所示。

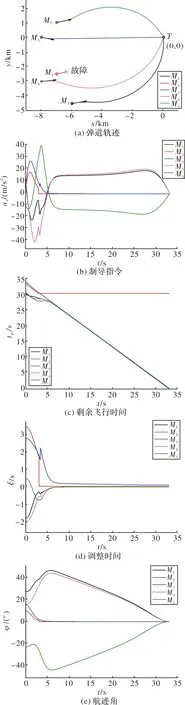
图5 仿真结果

从图5可以看出，当导弹2在第3 s受到干扰后，其剩余飞行时间保持不变，但是弹群中正常导弹的剩余时间估计值依然协同达成一致，得到收敛，同时各导弹在该制导律的导引下不断改变航迹，最终同时着靶，验证了该制导律的可行性。从细节处进行分析，从图5(b)、图5(d)可以看出，在导弹2受到干扰后，正常导弹的调整时间和制导指令发生了一定的波动，很快又得到了稳定收敛，这是滤波器的作用效果，制导指令在弹道末端最终收敛至0，保证了导弹在导弹末端的稳定性。从图5(c)导弹的剩余飞行时间图可以看出，在故障发生后，正常导弹的剩余飞行时间在制导指令的改变下得到了迅速调整，大约在仿真开始后的第8 s左右收敛一致。从图5(a)、图5(e)可以看出，导弹3(M3)的前置角迅速收敛至0，以最快的速度飞向目标，弹道近乎于一条直线，而其余导弹的前置角均先增大，进行相应的机动绕远以消耗剩余飞行时间等待导弹3的到来，最终各导弹的前置角均收敛至0，命中目标。

4 结论

针对时间协同作战弹群中，某些导弹受到复杂战场干扰，从而影响协同制导性能的问题，通过在制导律上整合模拟滤波器，提出了一种分布式抗干扰时间协同制导律，该制导律无需获取弹群中所有导弹的信息即可完成协同制导。通过仿真算例对该方法进行了仿真验证，仿真结果表明，在某些导弹受到干扰，无法正常工作时，该制导律可以快速滤除受扰导弹数据，导引其余正常导弹实现同时着靶，具备一定抗干扰能力。该方法可为后续抗干扰协同制导律的研究提供一定的参考。