基于匈牙利算法的多导弹阵地拦截指派规划

周洪喜，张 进，彭晨远,黎克波

(1 国防科技大学空天科学学院，长沙 410073；2 空天任务智能规划与仿真湖南省重点实验室，长沙 410073；3 63757部队，黑龙江佳木斯 154002)

0 引言

陆基导弹防御系统能够拦截敌方多种来袭目标，降低敌方军事威胁和战略威慑，有效保护己方重要价值目标。在实际运用中，采取多阵地协同防御拦截策略，可以提升拦截效果，在更短的时间内完成拦截任务，提升作战效能。安炳合等基于改进烟花算法对多导弹目标分配问题进行了求解[1]；柴华、刘鑫等将导弹可达域概念应用于拦截问题分析中，并用降维分析方法计算了导弹拦截窗口[2-3]；徐品高、任仙海等分别从防御策略和整数规划角度对排序问题进行了分析[4-5]。文中基于多导弹阵地协同拦截多目标问题，提出了一种基于匈牙利算法考虑多拦截窗口与发射时间间隔约束的拦截任务快速规划方法。

1 拦截窗口建模分析

1.1 拦截弹空间可达域建模

对于给定的拦截弹阵地，在建立拦截弹空间可达域模型时，仅考虑拦截弹的助推段控制，忽略中段与末段控制，以标称轨迹来建立空间可达域。在计算拦截弹的助推段飞行轨迹时，可供调节的参数有两个，一是拦截弹的发射方位角，决定拦截弹的纵向射面；二是拦截弹的助推段控制策略，即最终程序角，调节拦截弹助推段的飞行轨迹，给定发射方位角与最终程序角可唯一地确定拦截弹弹道，所有弹道的集合构成拦截弹的空间可达域。

考虑拦截弹的拦截效能，分析时仅考虑拦截弹上升段，即弹道最高点之前的部分，图1给出了发射方位角0°～360°，程序角分别为0°，25°，80°时的弹道轨迹。

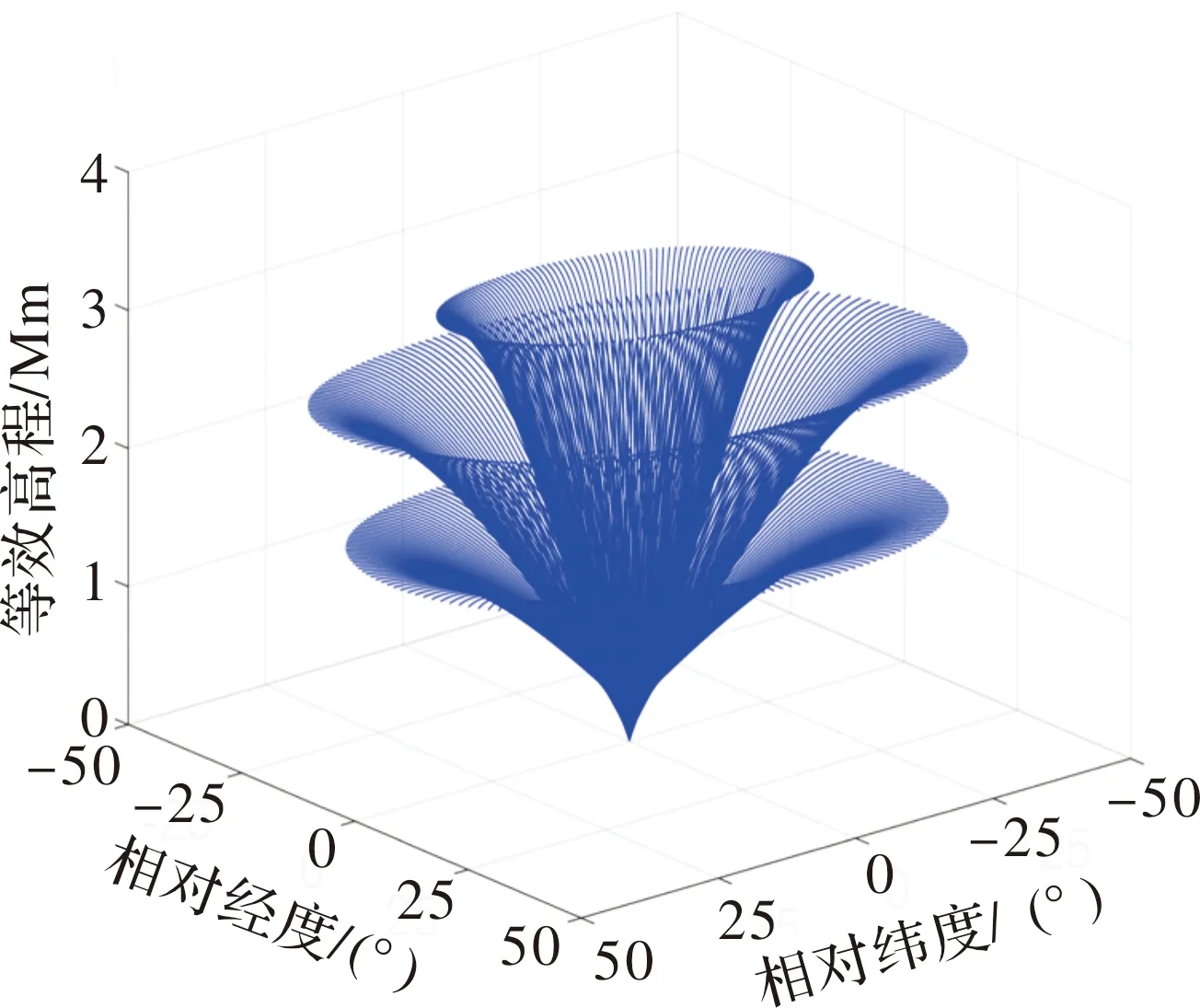
图1 不同程序角弹道覆盖范围

图1中最下层和最上层弹道分别为程序角0°和80°的弹道轨迹，程序角越大弹道越陡峭，由于拦截弹性能限制，程序角无法达到90°，所以拦截弹阵地正上方区域无法覆盖。拦截弹可达域就是由最下层和最上层弹道及中间弹道最高点所围成区域，如图2所示。

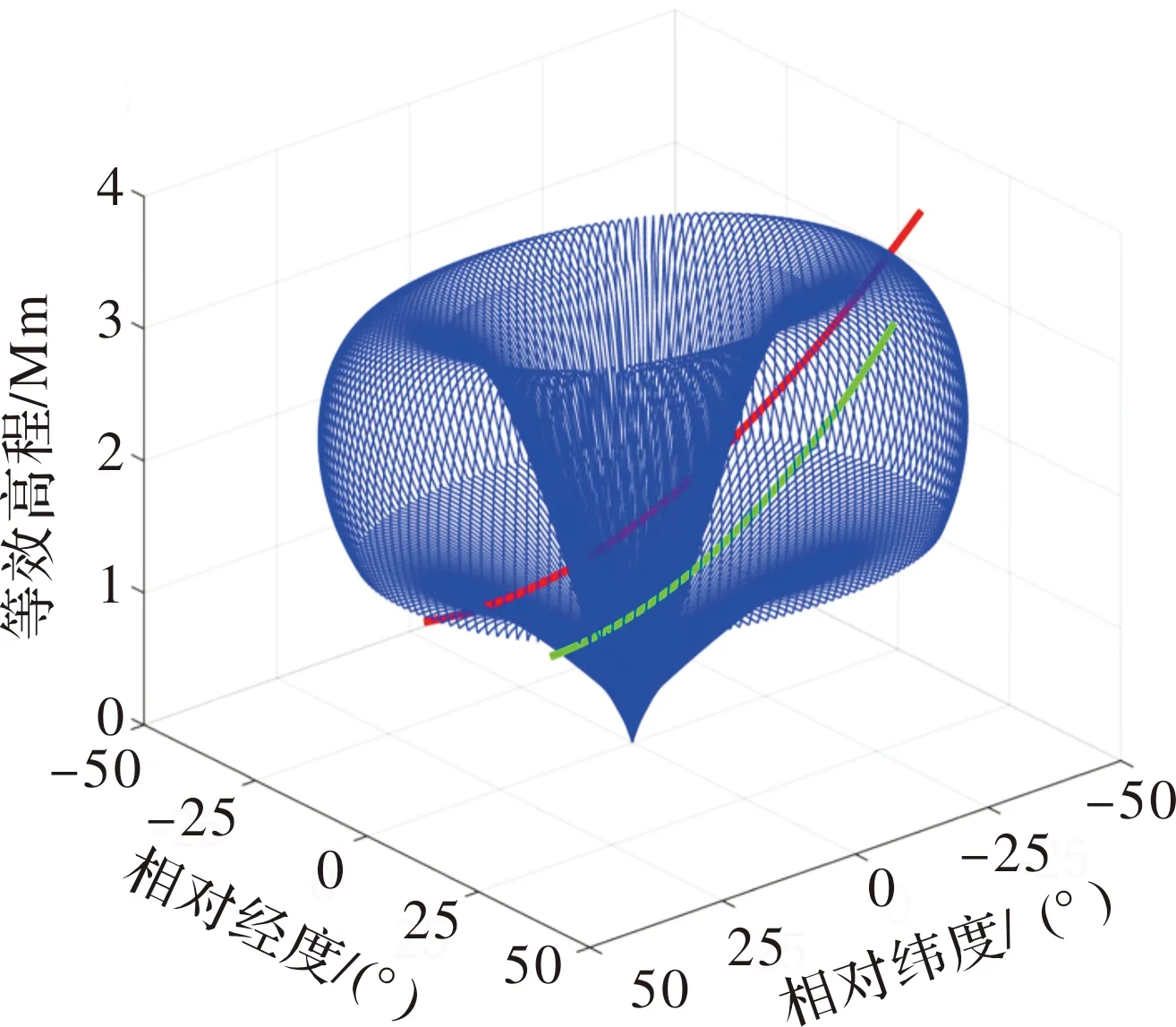
图2 拦截弹空间可达域

1.2 拦截窗口分析计算

在进行拦截窗口分析时，来袭目标轨迹与拦截弹可达域存在两种相交模式，如图2所示。当目标轨迹从可达域边缘穿越时拦截窗口是连续的；当目标轨迹从可达域中心穿越时，由于中心区域无法覆盖，拦截窗口分为两段。由于地球自转影响，拦截弹可达域模型呈现出复杂的空间几何构型，难以用解析的方式进行描述，给拦截窗口计算带来了困难。在实际求解过程中，通常采用降维分析的方法，即分别以等效高程和空间方位角截取可达域，将可达域离散为网格点，当来袭目标弹道落在离散网格点之间时拦截弹具备拦截能力，此时对应的时刻即为拦截窗口。

2 拦截任务指派问题模型和求解方法

2.1 平衡指派问题数学模型

对于n个拦截弹阵地拦截n个来袭目标的任务指派问题，称为平衡指派问题，规定每个阵地只拦截一个目标，且每个目标只由一个阵地进行拦截。已知aij表示第j个阵地拦截第i个目标的拦截窗口时间，[aij]称为时间系数矩阵。xij为决策变量，当xij=1时表示第j个阵地拦截第i个目标，否则xij=0。规划目标为任务完成总时间最少，即任务完成的总效率最高，于是平衡指派问题的数学模型可以表述为：

(1)

式中f为任务完成的时间和。

平衡指派问题可采用匈牙利算法进行快速求解。

2.2 任务完成时间最短的指派问题数学模型

对于平衡指派问题，其规划目标总效率最高，但在处理一些特殊问题时，例如应急支援保障或导弹防御拦截过程中，不仅关心任务完成的总效率，而且要求任务能够尽快完成，即完成最后一项任务所用时间最短，其数学模型可以表述为：

(2)

式中F为每次求得的参考解中的最大值。

任务完成时间最短的指派问题是一类非线性多目标规划问题，不能够直接运用匈牙利算法进行求解，白国仲证明了该问题可以通过对匈牙利算法改进后进行求解[6]，具体求解方法是：每次得到参考解中的最大值F后，对原时间系数矩阵按式(3)进行调整：

(3)

式中:g(aij)为原时间系数矩阵中元素aij经式(3)调整之后的值;M为任务计算时间周期。由此得到一组新的时间系数矩阵，重新利用匈牙利算法进行求解，重复上述操作，直到求得的结果不再变化时即得到了完成任务时间最短的解。

2.3 单阵地拦截多目标的任务指派问题求解

对于m个阵地拦截n个目标的任务指派问题，要求1个阵地最多可拦截p个目标，采用“1个阵地化成p个阵地法”和“加边补0法”，对原时间系数矩阵进行拓展[7]，生成一个pm阶方阵，如式(4)所示，其中列元素为原时间系数矩阵中的列元素重复p次，行元素中前n行与原系数矩阵中行元素相同，余下的pm-n行元素采用虚拟形式由0补齐，再按照任务完成时间最短的问题进行求解。

(4)

2.4 考虑拦截窗口时间间隔和多拦截窗口问题求解

由于同一阵地可以拦截多个目标，且拦截各目标时可能具有多个拦截窗口，每个拦截窗口具有不同的时长，在实际拦截中同一阵地连续拦截两个目标之间的时间间隔需要满足一定的发射准备时间要求，这时在进行任务规划时就需要综合考虑多个拦截窗口以及每个拦截窗口的时长情况[8]。首先利用前面的方法求解出一组最优解，然后对最优解中同一阵地拦截多个目标的时间间隔进行分析，看是否满足发射准备时间间隔要求，如果满足，则保留；如果不满足，则需要考虑后一拦截目标的窗口宽度和额外窗口情况后重新进行规划，其数学模型如式(5)所示：

(5)

式中T0为发射准备时间。

3 算例分析

考虑到地球自转对拦截弹空间可达域的影响，按照经纬度不同选取5个阵地进行可达域计算，阵地设置如表1所示。

表1 导弹阵地设置

选取5个来袭目标进行分析，任务分析开始时刻目标在地心地固坐标系下的空间状态如表2所示，分析时间为世界时2020年8月1日4时～8月2日4时共24小时。

表2 来袭目标初始时刻空间状态

给出每个阵地拦截对每个目标的拦截窗口及窗口宽度如表3所示。

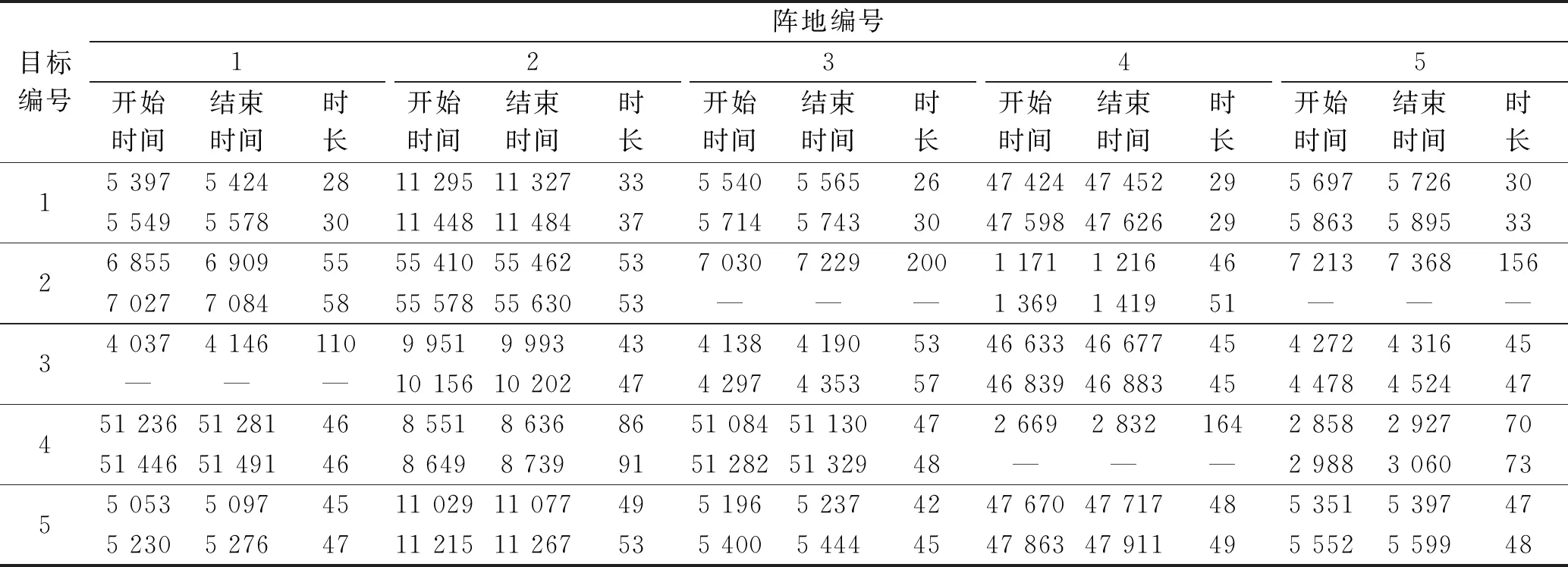
表3 拦截窗口 单位：s

选取每个阵地拦截每个目标的第一个拦截窗口生成的时间系数矩阵可表示为：

3.1 平衡指派问题求解

按照平衡指派问题，应用匈牙利算法对上述时间系数矩阵进行求解，得到的决策变量矩阵为：

由决策变量矩阵得到的按照平衡指派问题求解得到的拦截任务分配方案如表4所示。

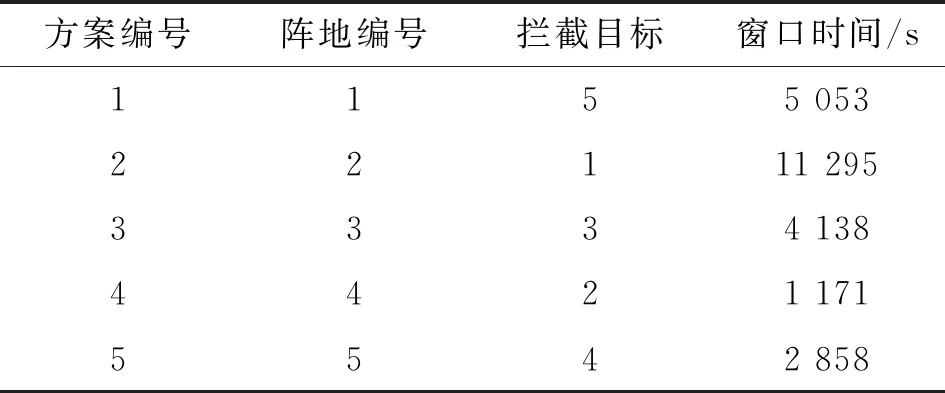
表4 平衡指派拦截任务分配方案

拦截用时时间和为24 515 s；用时最大时间为阵地2拦截目标1的时间11 295 s。

3.2 完成任务时间最短问题求解

完成任务时间最短，即完成最后一个任务用时最少，可以应用改进的匈牙利算法进行求解，同时分析同一阵地可以拦截多目标情况，运用“1个阵地化成p个阵地法”和“虚拟任务法”对系数矩阵进行拓展后再进行求解。

3.2.1 每个阵地最多拦截1个目标

应用改进匈牙利算法进行迭代求解，得到的决策变量矩阵为：

由决策变量矩阵得到按照完成任务时间最短求解得到的拦截任务分配方案如表5所示。

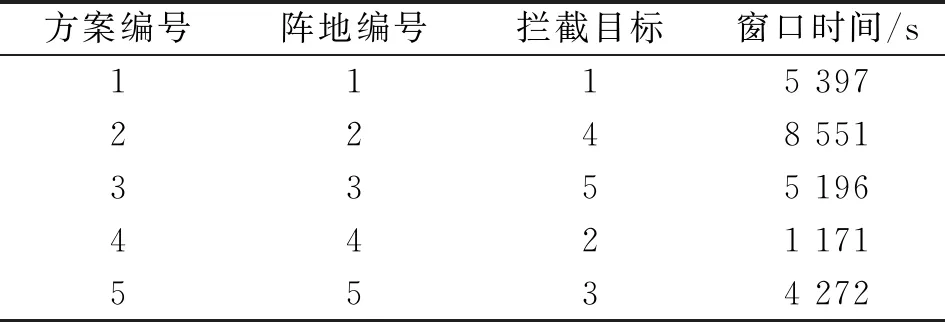
表5 每个阵地最多拦截1个目标的任务分配方案

拦截用时时间和为24 587 s；用时最大时间为阵地2拦截目标4的时间为8 551 s，相较于平衡指派的任务分配方案，任务能够提前2 744 s完成。

3.2.2 每个阵地最多拦截2个目标

每个阵地最多拦截2个目标，按照“1个阵地化成2个阵地法”和“虚拟任务法”对时间系数矩阵进行拓展，再应用改进的匈牙利算法进行求解，得到的拓展时间系数矩阵和决策变量矩阵分别为：

由决策变量矩阵得到每个阵地最多拦截2个目标时的拦截任务分配方案如表6所示。

表6 每个阵地最多拦截2个目标的拦截任务分配方案

阵地1先拦截目标5，再拦截目标1；阵地3拦截目标3；阵地4先拦截目标2再拦截目标4；阵地2和阵地5不进行拦截。拦截用时时间和为18 428 s；用时最大时间为阵地1拦截目标1的时间为5 397 s。与每个阵地只拦截1个目标的任务分配方案进行比较，拦截每个目标的时间和任务完成时间都明显缩短。

3.2.3 每个阵地最多拦截3个目标

每个阵地最多可拦截3个目标，按照“1个阵地化成3个阵地法”和“虚拟任务法”对时间系数矩阵进行拓展，再应用改进匈牙利算法进行迭代求解，得到每个阵地最多拦截3个目标的拦截任务分配方案如表7所示。

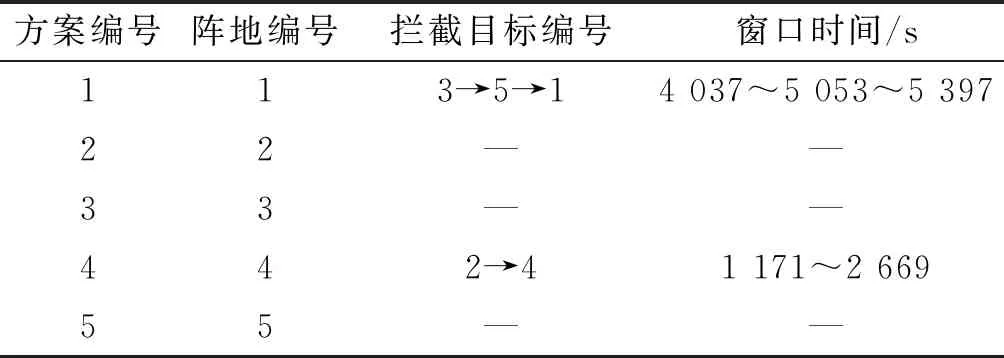
表7 每个阵地最多拦截3个目标的拦截任务分配方案

阵地1先拦截目标3，再拦截目标5和目标1；阵地4先拦截目标2再拦截目标4；阵地2、3和5不进行拦截。拦截用时时间和18 327 s；用时最大时间为阵地1拦截目标1的时间5 397 s。任务完成时间没有改变，但仅用2个阵地就可以完成拦截任务，可以尽量少的暴露阵地设施。

3.3 考虑任务准备时间和拦截弹飞行时间

实战应用中拦截弹拦截目标需要考虑拦截弹发射准备时间、拦截弹飞行时间以及地面雷达设备跟踪引导时间，通过分析，对于拦截目标弹道高度在700 km以下时，拦截弹飞行的时间均小于300 s，假设拦截弹发射准备时间为600 s，地面雷达设备需要在拦截弹发射前和命中目标后持续跟踪侦察目标300 s，拦截弹飞行过程中需要全程跟踪，所以一个阵地连续拦截两个目标的窗口时间间隔至少为900 s，如果再考虑其他因素则要求的时间间隔将远大于900 s。

表8给出了时间间隔为900 s、1 500 s、1 800 s、3 000 s、3 600 s时，每个阵地最多拦截2目标的任务分配方案。

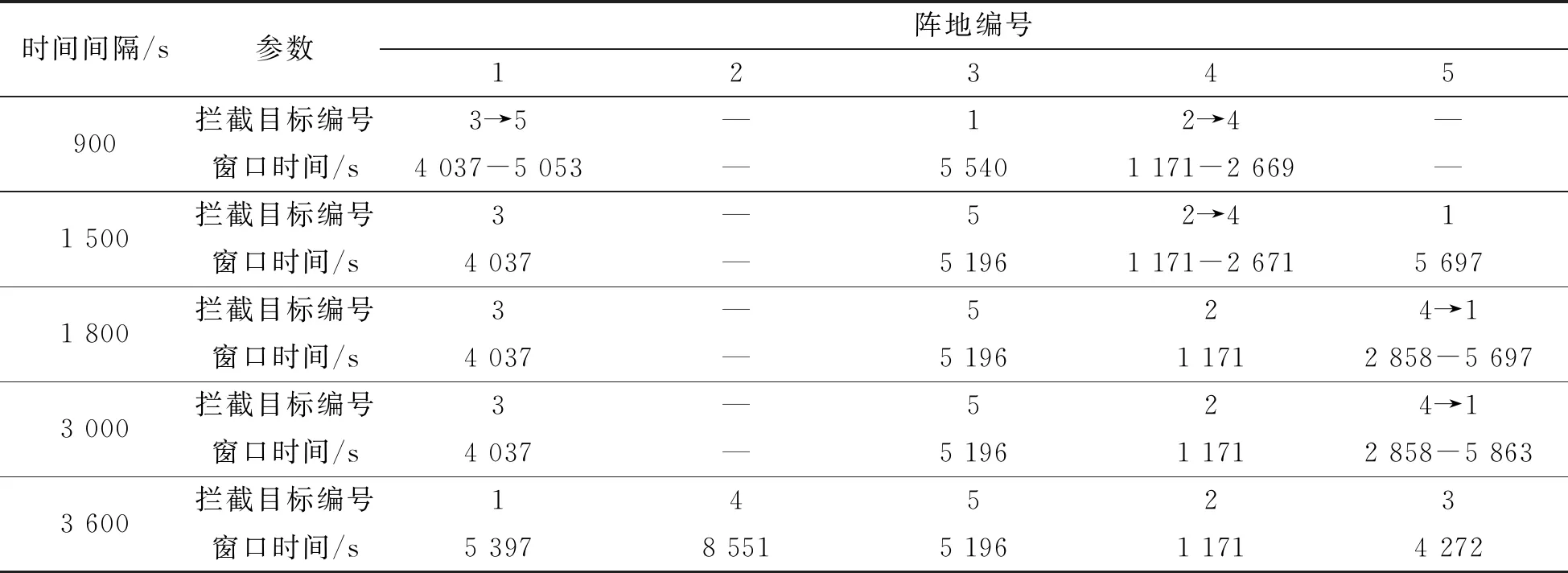
表8 不同时间间隔的任务分配方案比较

对比表6中不考虑时间间隔时的拦截任务分配方案，当时间间隔为900 s时，阵地1、3将拦截目标1、3进行了交换；当时间间隔为1 500 s时，目标1分配给了阵地5，且阵地4拦截目标4的窗口时间向后推迟了3 s；当时间间隔为1 800 s时，目标4分配给了阵地5；当时间间隔为3 000 s时，阵地5拦截目标1的窗口变为第二拦截窗口；当时间间隔为3 600 s时，每个阵地都只能完成一次拦截任务，问题转化为1个阵地拦截1个目标的情形，最终任务分配方案与每个阵地最多拦截1个目标的任务分配方案相同。当时间间隔不同时，拦截任务分配方案将发生较大变化，可以看出任务准备时间对拦截任务分配具有较大影响。

4 结论

通过改进的匈牙利算法对多阵地协同拦截多目标问题进行了规划求解。仿真结果表明：该方法能够快速得到多阵地协同拦截多目标情况下任务完成时间最短的任务分配方案，且分配算法隐含了完成所有任务时间和最小的条件，保证完成每个目标拦截任务的时间尽可能短。通过设置导弹阵地携带不同数量拦截弹以及不同任务准备时间间隔进行对比分析，结果表明：采用每个阵地多次发射策略，并缩短连续发射准备时间间隔，有利于快速完成拦截任务。