基于换相点换相的无刷直流电机无位置传感器控制*
2021-10-26徐海霞赵继永周大为
徐海霞,赵继永,周大为
(1.常州工业职业技术学院 智能控制学院,江苏 常州 213164;2.常州市易尔通电子有限公司,江苏 常州 213119)
0 引 言
无刷直流电机(BLDCM)以其结构简单、扭矩大、效率高和调速范围宽等优点广泛应用于仪表、家电、工控设备等领域中[1-2]。BLDCM一般通过安装在电机尾端的位置传感器来向电机控制器提供电机转子的位置信息。位置传感器的存在不仅增加了电机的制造成本,而且传感器的损坏风险也会降低电机在使用过程中的可靠性。因此,BLDCM的无位置传感器控制技术已成为国内外学者研究的重点之一[3-6]。
目前,BLDCM的无位置传感器控制算法中,基于反电动势过零点检测的转子位置估算方法及其衍生的方法应用最为广泛[7-8]。文献[9]利用了Buck变换器电感和电容的缓冲续流作用配合三次谐波检测法检测电机反电动势的过零点。文献[10]提出在上桥斩波下桥全开期间,比较非导通相端电压与中性点电压的关系,得到反电动势过零点信号。文献[11]提出增加单端初级电感变换器前级驱动电路来校正理想反电动势过零点与实际反电动势过零点间的相位差。文献[12]提出一种基于线电压差积分的方法检测和校正换相误差来估算电机的换相点。上述无位置传感器控制方法,当应用于高速电机控制时,由于滤波延时、转速和转矩波动、MCU计算时间等因素,会使得电机的反电动势过零点出现超前或滞后,造成换相不准确;当电机负载发生快速较大变化时易出现失步的现象。其他算法如定子电感法、神经网络算法等[13-15]虽在理论上得到了较好的验证,但实际的应用推广仍较少。
针对上述问题,本文提出了一种新型的无传感器控制算法,该算法综合BLDCM三相绕组的反电动势特性,通过分析在控制算法的换相位置点电机反电动势存在的规律,利用该规律并结合电机反电动势与转速的关系,从而获得BLDCM的换相位置。该算法规避了传统过零点算法的延时估算过程,引入查表法,使得实现过程更为简单,适于推广,特别是在高速电机控制中具有很大优势。同时,本文提出了一种新型的电机反电动势检测电路,以取代传统的三相电压检测电路,该电路在成本、资源需求等方面比传统电路具有很大优势,更适用于成本敏感度较高的应用场合。
1 基于电机中心点的反电动势检测电路及分析
BLDCM无传感器算法的检测电路需3个ADC端口分别检测电机的三相电压,在许多成本要求低的场合并不适用。本文提出一种在电机外部重构电机中性点的电路,并通过测量该点电压来获取电机悬空相的反电动势,如图1所示。

图1 中性点重构电路
电阻R1、R2和R3用于外部重构电机的中性点,且R1=R2=R3,阻值远大于电机定子绕组的内阻,一般10 kΩ以上。利用电阻R4和R5对外构的中性点电压进行分压,从而获得适于MCU采样的电压。
传统BLDCM的控制算法一般采用开通电机一相的上管和另外一相的下管方式来驱动BLDCM转动。假设控制系统在电机A相上管和电机B相下管导通的状态下,图1所提重构电路可转化为图2所示的等效电路。

图2 驱动状态下的等效电路
当不考虑电机定子绕组间互感时,可以得到:
(1)
式中:UN为电机中性点电压;Ubat为系统供电电压即电池电压;Ia、Ib和Ic为电机三相绕组中通过的电流;Ra、Rb为电机A相和B相绕组的电阻;La、Lb为电机A相和B相绕组的电感;ea和eb为电机A、B相绕组的反电动势。
由于外部选用电阻要远大于电机定子绕组的内阻,故Ic可近似为零。若假设电机三相绕组相互对称,即Ra=Rb=Rc,La=Lb=Lc,则ea+eb+ec=0,式(1)可以简化为
2UN=Ubat+ec
(2)
设R1=R2=R3=R,采样电压Uo为
(3)
将式(2)代入式(3)可得:
(4)
由式4可见,在外部匹配电阻、系统供电电压已知的条件下,根据采样电压Uo可以准确计算出悬空相的反电动势ec。
(5)
2 基于换相点的换相算法
电机转动过程中,BLDCM定子三相绕组产生的反电动势相位差为120°,以反电动势为正弦波的BLDCM作为分析对象,反电动势为梯形波的BLDCM分析与之同理。
BLDCM的控制算法输出的电压方向是抑制电机最大反电动势的方向,即开通电机三相中电压最大相对应的上管和电机三相电压中最小相对应的下管。电机反电动势与驱动桥臂导通关系如图3所示。其中,H->为上桥臂开启的对应相,L->为下桥臂开启的对应相。
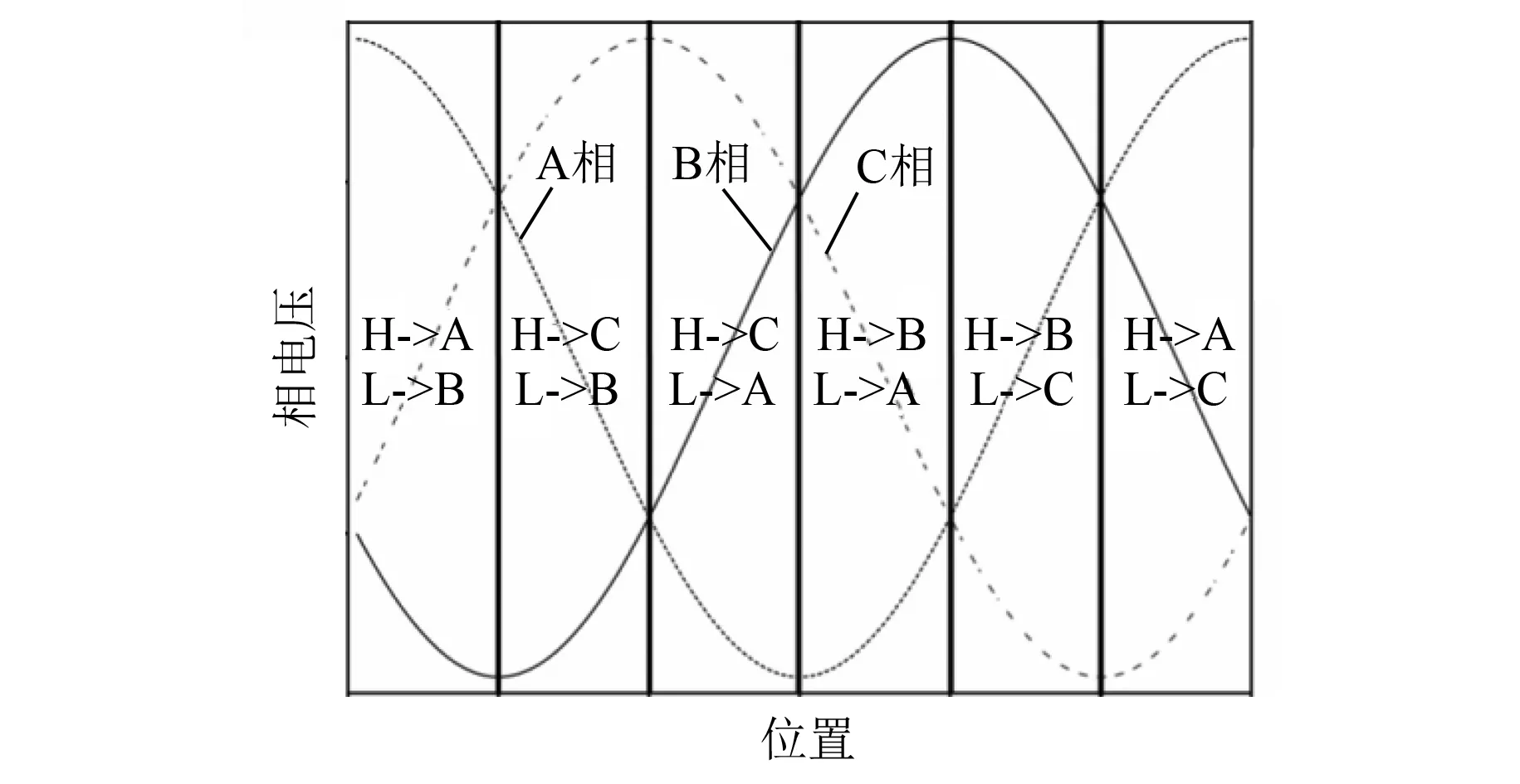
图3 驱动状态与电机反电动势的关系
分析图3可以发现控制算法中发生换相的位置具有以下特性:(1)非换相桥臂的反电动势达到幅值电压;(2)需换相的2个桥臂反电动势相等。根据电机三相反电动势之和为零的特性,可以得出结论:当电机发生换相时,其悬空相的反电动势为其反电动势幅值的一半。
BLDCM的反电动势幅值与其转速成正比例关系,表达式如下:
ep=Ke×ω
(6)
式中:ep为电机反电动势的幅值;Ke为反电动势常数;ω为电机转动电子频率。
将式(6)中的电子频率转换为电子周期,并将周期分为6个等分扇区,可计算电机在换相位置时悬空相的相电压:
(7)
式中:es为换相点悬空相的反电动势;Te为电机转动中每个驱动扇区的时间。
通过对比由采样电压Uo计算出的悬空相反电动势ex(x为悬空相)与由转速估算的悬空相电压es,从而确定电机的换相点。当悬空相反电动势处于上升的阶段时,ex>es可换相;当悬空相反电动势处于下降的阶段时,ex 为提高电机驱动过程中的软件执行效率,将es预先计算好存放于数组中,驱动电机的过程中,直接提取数组中的换相点电压与当前检测值ex进行比对。其中,数组中元素es的计算方式如下: (8) 式中:ΔT为芯片执行换相定时中断的周期值;n为数组元素序列号即换相后该定时中断发生的次数。 该算法的简要执行步骤如下。 步骤1:根据被控电机参数代入式(8)产生换相点电压数组es(n)。 步骤2:产生定时中断,n=0。 步骤3:驱动上桥导通时,由ADC端口获取采样电压Uo,计算当前悬空相电压值ex。 步骤4:若悬空相电压处于上升期,当ex>es(n)时,跳转到步骤5,否则n=n+1,跳转到步骤3;若悬空相电压处于下降期,当ex<-es(n)时,跳转到步骤5,否则n=n+1,跳转到步骤3。 步骤5:执行电机换相,n=0,跳转到步骤3。 为验证本文所提方法的有效性和可行性,选用G40-LB07-64S35型无位置传感器的BLDCM作为试验对象。该电机的额定功率为1 500 W,电机额定转速为10 000 r/min,额定电压40 V,转子极对数为7。 为验证所提方法的动态响应优越性,通过仿真对比过零点检测算法与本文所提算法的换相表现。根据被测电机特性,模拟外部施加负载时令电机在0.1 s内由6 000 r/min均匀降至1 000 r/min的过程,其单相的反电动势变化如图4所示。 图4 电机相电压变化趋势 选取自0.05 s开始至0.07 s这段时间,分别采用过零点检测算法和本文所提的换相算法执行电机的换相操作。图5是电机三相电压在这段时间的变化趋势,并展示了采用2种不同算法根据当前的相电压执行换相操作的表现。 图5 2种电机换相算法的仿真对比 在图5中,图5(a)~图5(c)为电机三相电压的变化趋势。图5(d)为基于过零点检测的换相算法提供的电机换相信息,每当产生一次换相,则位置数增加1,位置数在1~6区间内循环。图5(e)为基于本文的换相算法提供的电机换相信息。 由图5可见,过零点换相算法在电机转速发生明显变化时,其换相扇区的时间发生了明显的不对称,随时间推移不对称性会显著增加,从而导致这种换相操作易于出现失步现象。该现象是由于在负载变化较大、速度变化较快的情况下电机的反电动势过零点并非一个扇区的中心点。而本文所提算法在整个时间段均较为准确地选择了换相位置,具有较强的动态响应性能。 为验证本文所提方法的实用性和可推广性,电机控制器选用意法半导体公司的STM32FEBKC6作为主控MCU,试验时芯片选用的主频为48 MHz。构建BLDCM驱动桥臂的MOSFET选用新洁能公司的NCEP85T14。PWM模块的输出频率为15.6 kHz。电机换相计算的中断频率设置为50 kHz。试验采用稳压电源为控制器供电,试验电压为40 V。试验测试装置如图6所示。 图6 测试装置 试验中未采用霍尔传感器验证算法换相准确性,主要是由于传感器的安装精度不足以作为衡量算法的标准。本次试验使用的电机未安装位置传感器,可根据电机相对地电压的对称性来判断其换相精度。 为验证算法的动态响应性能,将控制器的母线限流值设定为45 A,相电流保护值为100 A,将电机转至7 000 r/min,对电机突然施加2.5 N·m的重负载,观察被测控制器单相相电流及相对地电压的变化波形。试验波形如图7所示。 图7 突加负载时电机相电流和相对地电压的变化趋势 在图7中,示波器的2通道为电机A相的相对地电压,示波器4通道为A相的相电流。通过对图7的分析可知,在其转速下降的末期,其相电流峰值已达到100 A左右,此时控制器需进行相电流保护,但通过电机相对地电压波形和相电流波形来看,此时控制器执行的换相操作依然正常。 为验证本文所提算法在不同速度区间的换相性能,利用恒转速的控制方式将被测电机分别转动至2 000、4 000、6 000、8 000、10 000 r/min,观察其单相的相对地电压及其母线电流的波形,每组试验均对电机施加0.2 N·m的负载。不同转速下试验波形如图8~图12所示。其中示波器的2通道均为相对地电压波形,4通道均为控制器的母线电流波形。 图8 电机在2 000 r/min时电压及电流波形 图9 电机在4 000 r/min时电压及电流波形 图10 电机在6 000 r/min时电压及电流波形 图11 8 000 r/min电压及电流波形 图12 10 000 r/min电压及电流波形 由上述试验结果分析可见,所提算法在不同转速下均具有良好的换相效果。因此,本文阐述的方法可以有效替代霍尔传感器实现BLDCM的无位置传感器控制。 (1)从外部构建电机中性点的电路出发,分析了其检测电压在电机驱动状态下可直接反馈电机悬空相电压的规律,利用该规律得到一种新型的电机反电动势检测电路。 (2)分析了BLDCM在换相点时电机相电压的规律,并利用该规律提出了一种有别于过零点检测而直接锁定换相点的BLDCM无位置传感器的换相算法。 (3)试验结果表明,本文所提方法在动态响应性能上具有较大优势,实现简单,在电机各个转速区间均具有良好的换相效果。 对比其他的BLDCM无位置传感器控制算法,本文所提方法实现简单,成本要求较低,更适于在工业生产中应用和推广。目前,本文研究成果已成功地大批量应用于常州某电动工具公司的产品中,并取得了良好的效果。3 试验仿真及分析
3.1 仿真测试
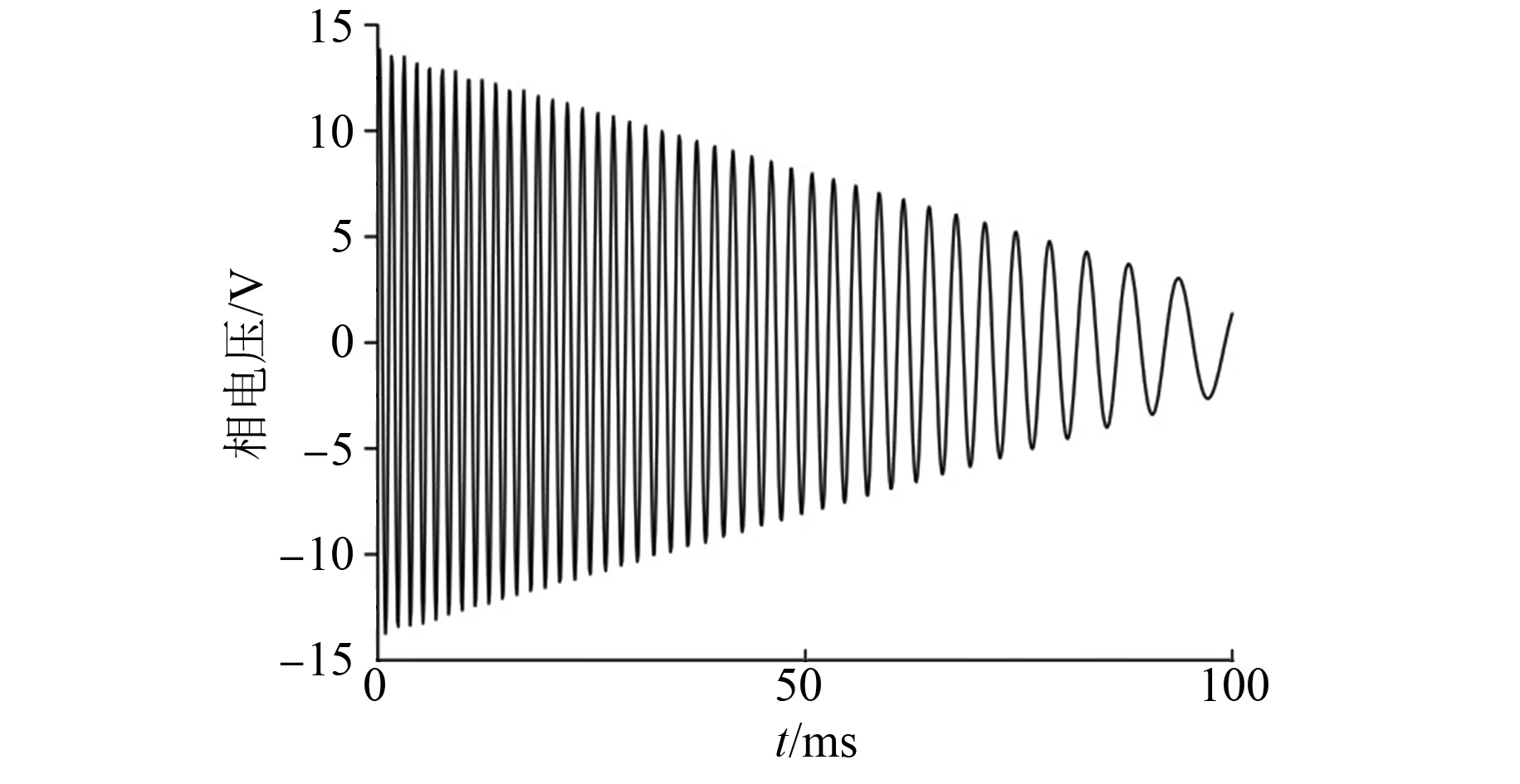

3.2 试验测试


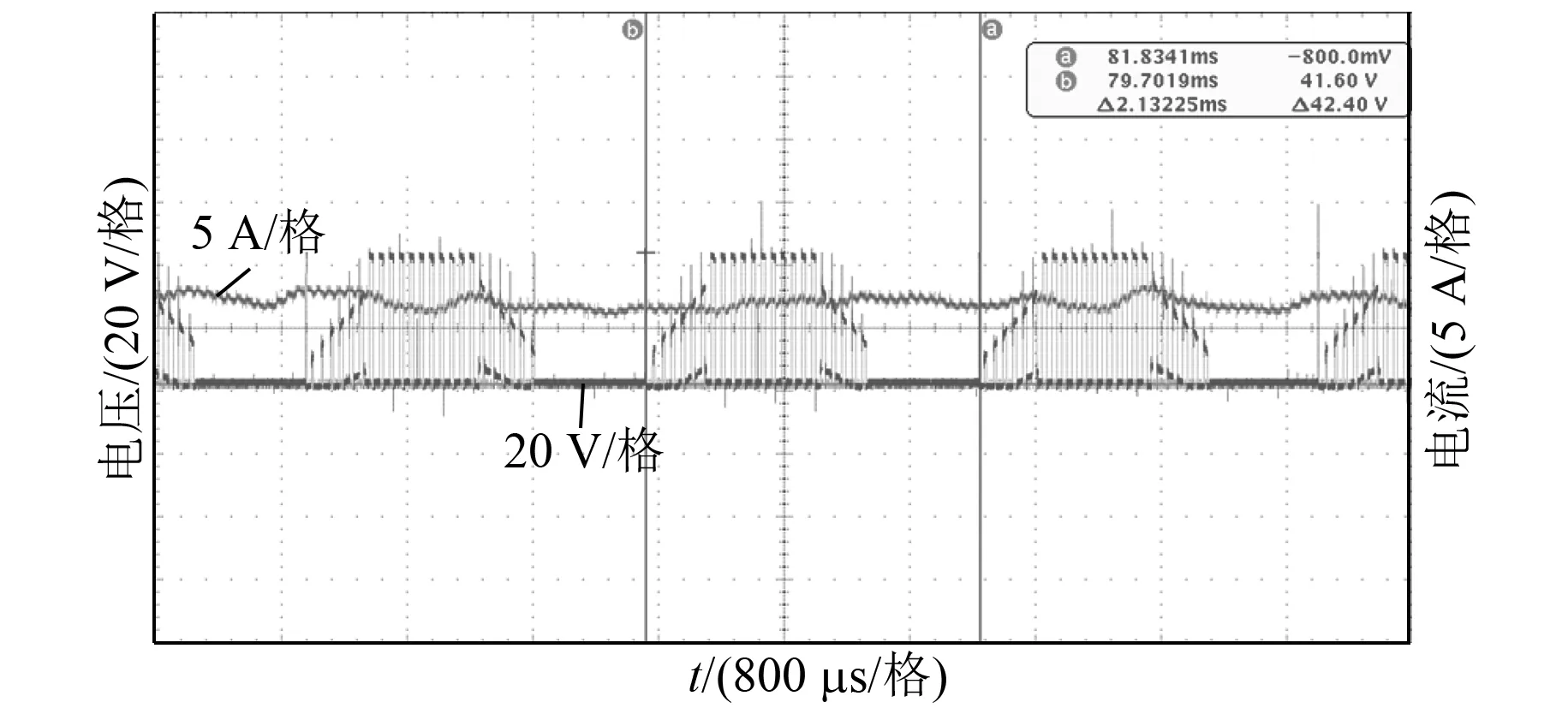


4 结 语
