双向准Z源逆变器驱动永磁同步电机的快速有限集模型预测控制

曾 礼，杜 强，陈阳琦

(西安中车永电捷通电气有限公司,陕西 西安 710000)

0 引 言

Z源逆变器(ZSI)作为单级式DC/AC拓扑结构，不仅可以实现升压和逆变控制，而且允许直通(ST)、无需死区时间，具有电压调节范围宽、输出电压畸变小及可靠性高等优点[1]。基于ZSI改进的准Z源逆变器(qZSI)，在保留ZSI优点的同时，可以抑制起动冲击电流，减小电容电压应力[2]。通过给qZSI二极管并联可控器件构成双向qZSI，克服了qZSI轻载或电感量较小运行时，其电感电流工作于断续模式的非正常工作状态的缺点，并且还可以实现能量的双向流动[3]。当其应用于电机驱动系统时，可实现再生能量的回馈，避免能量以电阻热量或其他形式耗散。永磁同步电机(PMSM)因具有体积小、功率密度大、质量轻、效率高及运行安全可靠等优点在工业应用中正逐步替代异步电机[4-6]。将双向qZSI与PMSM相结合，可充分发挥各自的优势，提高整个传动系统的效率以及PMSM的调速范围、减小转矩低频脉动[7-10]。

有限集模型预测控制(FCS-MPC)因兼具控制原理简单、易处理系统非线性约束、动态响应快等优点，成为功率变换器及变频调速系统中倍受推崇的一种优化控制方案。FCS-MPC通过建立被控量的预测数学模型和代价函数，遍历所有开关状态来计算被控量下一时刻的值，最后采用使代价函数最小的开关状态。已有学者将FCS-MPC应用于ZSI光伏并/离网网逆变器[11]、三相四桥臂qZSI[12-13]、储能型qZSI[14]及qZSI驱动PMSM的调速系统[15-16]等，被控系统具有良好的静、动态性能。另外，对于PMSM，相较于模型预测转矩控制，模型预测电流控制代价函数的量纲一致，可避免权重系数的设计问题[17]。

针对双向qZSI驱动PMSM系统提出一种快速FCS-MPC策略。分析了系统工作原理，推导了双向qZSI的电感电流和PMSM的三相电流数学表达式，并利用前向欧拉公式得到其预测模型；其次，结合SVPWM算法，设计了系统的快速FCS-MPC策略。通过阻抗源网络电容电压闭环及PMSM的电磁功率前馈得到电感电流给定值，利用电感电流代价函数确定是否选择ST状态。在非直通(NST)状态下，仅需目标矢量所在扇区中的4种开关状态参与PMSM定子电流及代价函数的在线计算。最后，通过MATLAB/Simulink验证所提控制策略的有效性。

1 双向qZSI驱动PMSM的工作原理及数学模型

1.1 工作原理

双向qZSI驱动PMSM系统的主电路结构如图1所示，主要由直流电压源、双向qZSI(双向准Z源网络级联三桥臂逆变器)及PMSM构成。其中，双向准Z源网络由功率管S1、电感L1、L2及电容C1、C2构成。由于功率管S1的存在，可以实现能量双向流动。当系统处于牵引工况时，PMSM为电动机，能量从直流电源流向PMSM，当系统处于制动工况时，PMSM为发电机，能量从PMSM反馈到直流电源。

图1 双向qZSI驱动PMSM系统拓扑

在2种工况下，双向qZSI具有ST和NST 2种工作状态，具体等效电路及工作波形分别如图2(a)、图2(b)所示。在牵引工况时，qZSI功率因数为正，电感电流为正值，直流链电流为正的脉冲波，ST状态时，幅值最大。在制动工况时，qZSI功率因数为负值，电感电流为负值，直流链电流为负值的脉冲波，ST状态时，幅值最大。

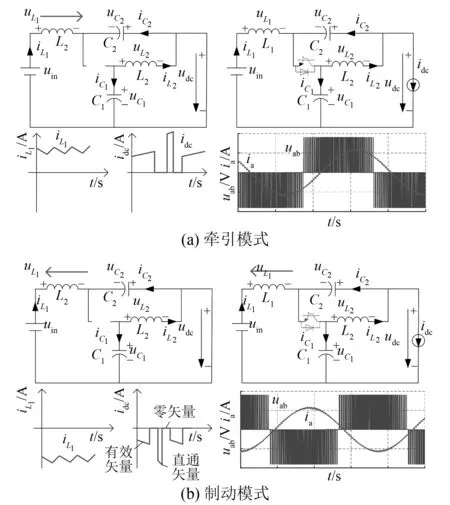
图2 系统工作等效电路

1.2 双向qZSI数学模型

ST状态时，开关S1断开。此时，电感电压uL1和uL2、直流链电压udc及开关S1电压分别为

(1)

NST状态时，开关S1闭合。此时，电感电压uL1和uL2、直流链电压udc及开关S1电压分别为

(2)

假设控制周期为Ts，ST时间为Tsh，稳态条件下电感电压在一个开关周期内的平均值为0，即：

(3)

由式(3)可求得稳态时准Z源网络电容电压uC1和uC2表达式分别为

(4)

式中：D为ST占空比，D=Tsh/Ts。

结合式(2)和式(4)得到直流链电压幅值为

(5)

逆变器侧输出电压矢量可表示为

(6)

根据式(6)，可得到qZSI的9种开关状态及其所对应电压矢量，如表1所示。

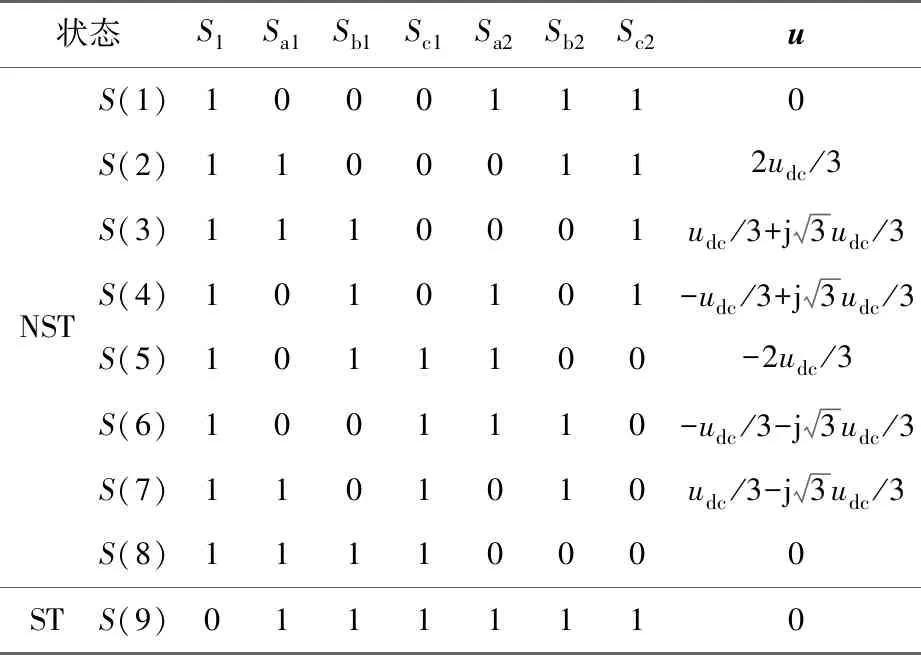
表1 qZSI逆变器开关状态及其对应电压矢量

1.3 PMSM数学模型

表贴式PMSM在αβ坐标系下的数学模型为

(7)

式中：uα、uβ为定子电压在αβ坐标系中的α、β轴分量；iα、iβ为定子电流在αβ坐标系中的α、β轴分量；θr为转子转过的机械角度；Ls为定子电感；Rs为定子电阻；ψf为转子永磁体磁链；ωr为电机机械转速；p为电机极对数。

2 双向qZSI驱动PMSM的快速FCS-MPC

2.1 阻抗源电感电流预测控制

为了实现对电机转速和电流的控制，需要保证双向qZSI的直流链电压稳定，直流链电压将影响逆变器的输出电压。qZSI直流链电压为脉冲方波信号，无法直接检测与反馈控制[18]。但基于式(2)可以看出直流链电压为2个电容电压之和，因此可以通过uC1和uC2实现直流链电压控制。另外，引入PMSM电磁功率前馈以加快直流链电压调节的动态响应，进而得到电感参考电流表达式为

(8)

式中：udc_ref为直流链电压参考值；kp、ki为直流链电压闭环控制器的比例系数和积分系数；kpm为电磁功率前馈系数；

依据式(1)、式(2)，并采用前向欧拉逼近法，可得到ST与NST状态下双向qZSI电感电流的表达式分别为

(9)

(10)

为了实现双向qZSI升压控制，引入如式(11)所示的代价函数，若giL<0，则选择ST状态，否则在NST状态下进行PMSM预测电流控制。giL表达式为

(11)

式中：iL1_ref(k+1)为k+1时刻电感电流参考值，可由式(8)计算。

2.2 电机电流预测控制

当直流链电压幅值控制恒定时，通过调节逆变器输出电压和频率便可实现对电机转矩和转速的控制。PMSM转矩电流分量参考值iq-ref由转速闭环生成，进而便可得到定子电流参考值在α、β轴上的分量表达式为

(12)

(13)

式中：nr_ref为电机转速参考值；kp1、ki1为电机转速闭环控制器的比例系数和积分系数。

同理，根据式(7)可得PMSM定子电流的预测表达式为

(14)

同时，为实现对PMSM的定子电流控制，引入的价值函数：

(15)

式中：iα_ref(k+1)、iβ_ref(k+1)为k+1时刻PMSM定子电流参考值分别在α、β轴上的分量。

为了减小在线计算量，参考SVPWM调制算法，规定每个扇区内仅2个有效矢量和2个零矢量参与计算，这样一个计算周期内，开关状态由8次遍历降低至4次遍历，在线计算量减半。qZSI电压空间矢量如图3所示。以第Ι扇区为例进行说明，当目标电压矢量位于第Ι扇区时,仅使电压矢量U4、U6、U0、U7参与PMSM电流预测和代价函数计算，无需遍历其他扇区的有效电压矢量。为此，首先需要求得k时刻的最优电压矢量U(k)，令iα_ref(k+1)、iβ_ref(k+1)的电流值与给定值一致，则可求的U(k)在α、β轴上的分量表达式为

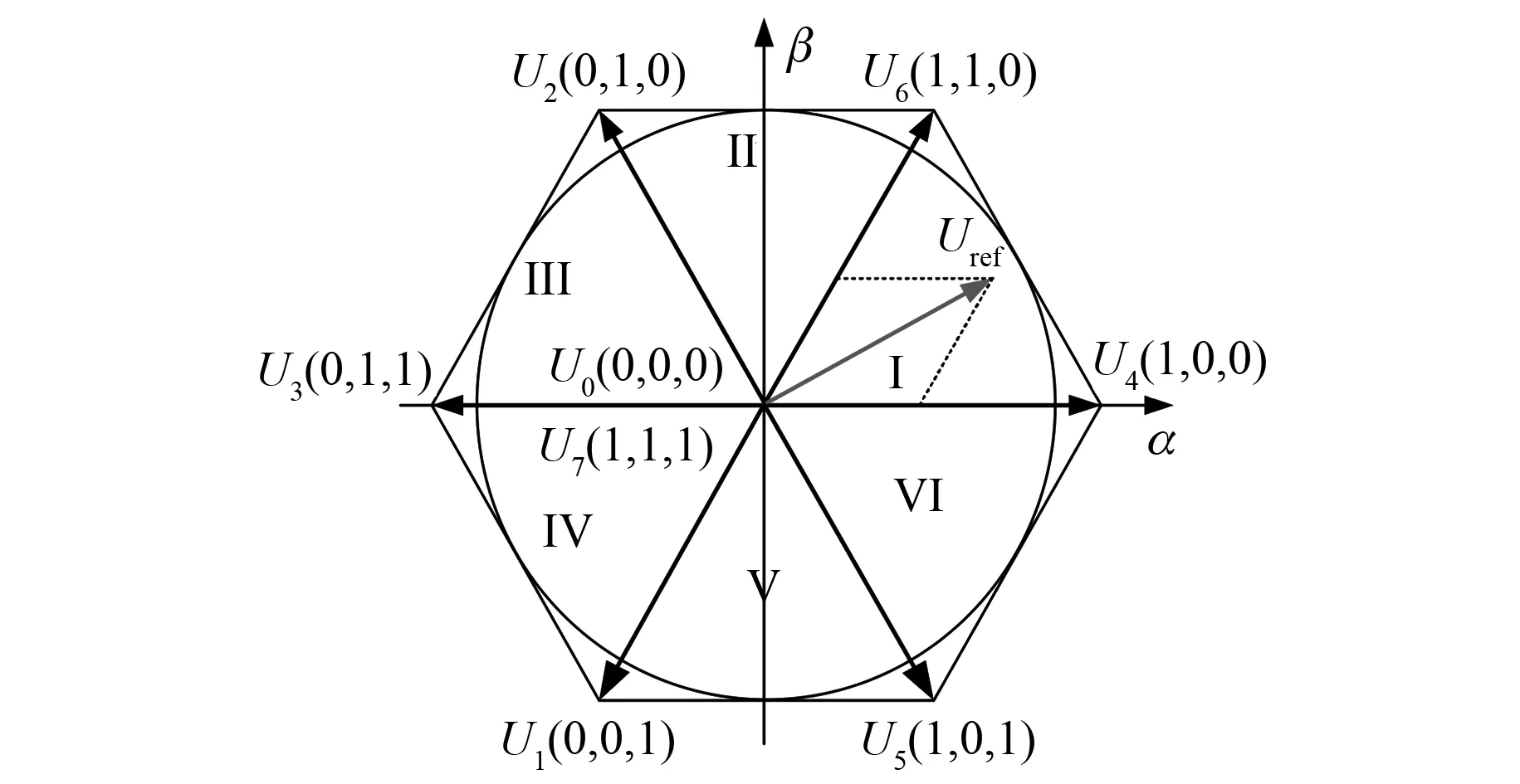
图3 电压空间矢量图

(16)

定义变量ur1、ur2、ur3分别为

(17)

并定义扇区指针N：

N=sgn(ur1)+2sgn(ur2)+4sgn(ur3)

(18)

同理，可以得到其他扇区下参与控制计算的电压矢量如表2所示。

表2 参与控制的电压矢量

2.3 控制算法

综上所述，由双向qZSI驱动PMSM的控制结构和控制流程分别如图4和图5所示。

图4 双向qZSI驱动PMSM的快速FCS-MPC结构

图5 双向qZSI驱动PMSM的快速FCS-MPC流程

对PMSM的定子电流、转速以及双向qZSI电感电流、电容电压等物理量进行采样。由直流链电压闭环及PMSM电磁功率前馈生成电感电流参考值。依据电感电流预测模型得到ST及NST状态下的电感电流预测值，并计算电感电流代价函数，以确定是否选择ST状态，若选择ST状态则直接将所有开关置1。反之，依据定子电流参考值计算目标电压矢量，并依据该目标矢量确认参与在线计算的基本电压空间矢量。通过PMSM转速闭环生成内环电流参考值，通过快速FCS-MPC在4种开关状态下选择最优开关状态，从而实现对定子电流的跟踪。通过上述控制流程便可实现双向qZSI的升压和PMSM转速的控制。

3 仿真与分析

在MATLAB/Simulink中搭建双向qZSI驱动PMSM系统仿真模型，系统仿真参数如表3所示。

表3 系统仿真参数参数

3.1 系统稳态运行仿真分析

设置电源电压uin=240 V，电机转速参考值n_ref=2 000 r/min、负载转矩Tm在0.1～0.2 s、0.2～0.3 s的值分别为10及-10 N·m，其中，电机在0.1～0.2 s为牵引稳态，0.2～0.3 s为制动稳态。分别对基于快速矢量选择的FCS-MPC及传统枚举的FCS-MPC下的系统进行仿真，结果如图6、图7所示。由于2种控制策略下的波形完全一致，因此仅对直流链电压和逆变器输出线电压进行对比，其他均为基于快速矢量选择FCS-MPC下的波形。

图6为系统稳态运行时PMSM侧仿真结果。图6(a)为电机转速波形，可以看到牵引/制动工况下稳态时电机转速均为2 000 r/min，与参考转速值一致。图6(b)为电机电磁转矩波形，电机电磁转矩与负载转矩相等，分别为10 N·m和-10 N·m，进而保证电机恒速运转。图6(c)为电机定子电流波形，定子电流为三相对称的正弦波，由于牵引及制动工况下转矩幅值和转速相同，因此2种工况下电流幅值及频率一致。图6(d)为基于快速矢量选择FCS-MPC和枚举法的FCS-MPC下的逆变器输出线电压波形(包括牵引及制动阶段的对比)，可以看到2种控制下波形完全一致、控制效果相同。

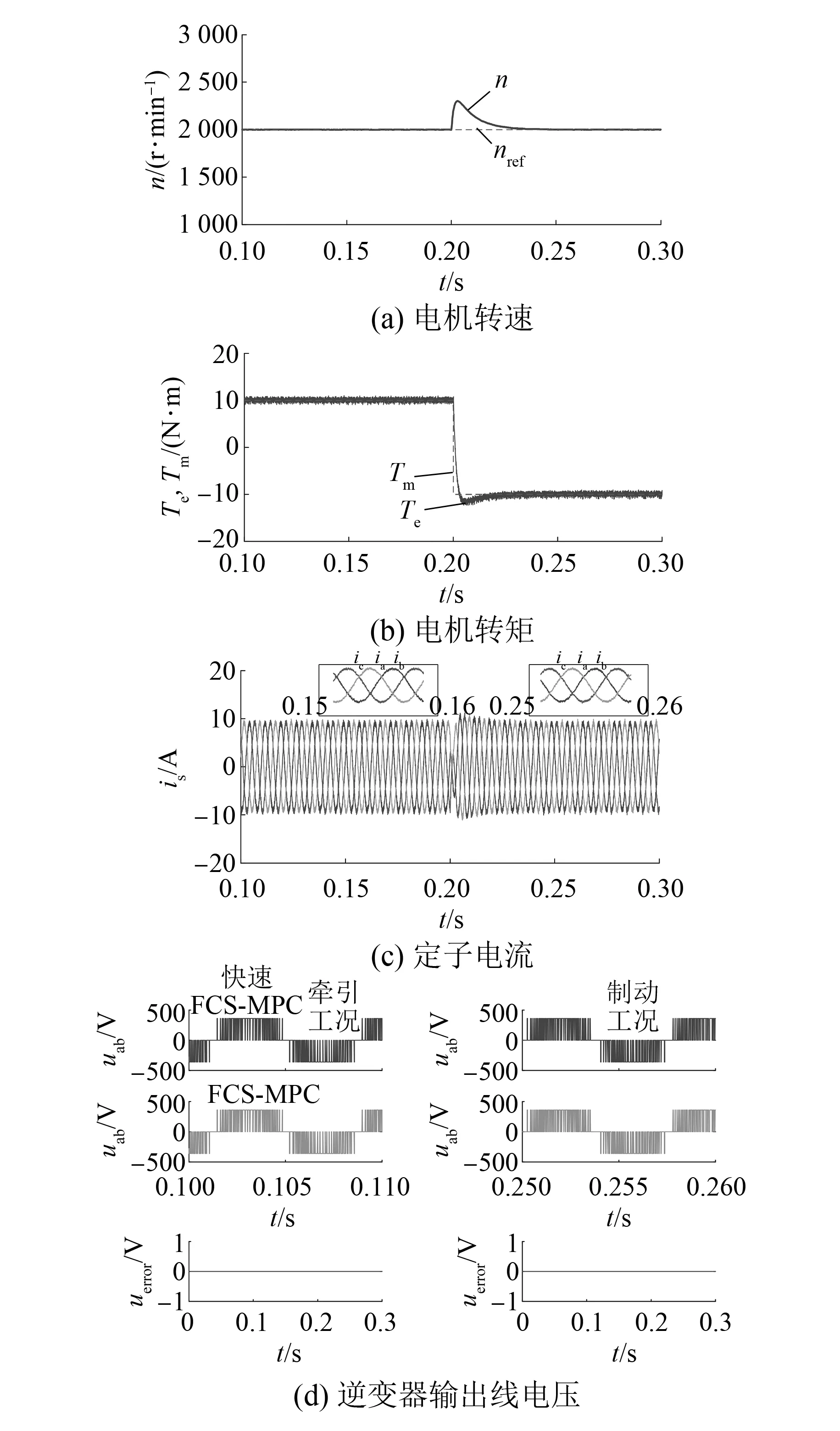
图6 系统稳态运行PMSM侧仿真结果

图7为系统稳态运行时双向qZSI侧仿真结果。图7(a)为阻抗源网络的电感电流波形，电感电流在牵引工况约为10 A，再生制动工况下约为-10 A，实现了能量的双向流动控制；图7(b)和图7(c)分别为电容电压和直流链电压波形，电容电压uC1稳态值为300 V，直流链电压幅值实测为360 V，与参考电压一致。图7(d)为基于快速矢量选择FCS-MPC和枚举法的FCS-MPC下的的局部放大直流链电压波形(包括牵引及制动阶段的对比)，可以看到在0.001 s(40个控制周期)内插入了7个ST状态，每次ST时间为一个控制周期。2种控制下波形完全一致、控制效果相同，说明2种控制方法的本质相同。

图7 系统稳态运行双向qZSI侧仿真结果

以上仿真结果表明所提FCS-MPC可使系统实现对给定值的无静差跟踪，具有良好的稳态性能。同时，与基于枚举法的FCS-MPC策略相比，在取得相同控制效果的同时可以减小在线计算量。

3.2 系统暂态运行仿真分析

设置电源电压uin在225～250 V之间变化。设置牵引工况(0～0.2 s)、再生制动工况(0.2～0.4 s)下的负载转矩分别为8、-8 N·m。电机转速给定值如图8(a)所示，从200 r/min在0.1 s内线性升高至2 000 r/min，随后从2 000 r/min在0.13 s内线性下降至400 r/min。分别对基于快速矢量选择的FCS-MPC及传统枚举的FCS-MPC下的系统进行仿真，结果如图8和图9所示。2种控制策略下的波形完全一致，因此仅对直流链电压和逆变器输出线电压进行对比，其他均为基于快速矢量选择FCS-MPC下的波形。

图8 系统暂态运行PMSM侧仿真结果

图8为系统暂态运行时PMSM侧仿真结果。图8(a)为电机转速的波形图，可以看到实际转速可以良好地跟踪给定转速值，当负载转矩突然阶跃时，电机转速经过一个超调暂态过程后快速恢复到给定转速参考值。图8(b)为电机电磁转矩的波形图，在转速指令线性上升阶段，电机实际电磁转矩大于负载转矩，进而实现系统牵引加速运行；在转速指令恒定时，电机电磁转矩与负载转矩相等；在转速指令线性下降阶段，电机实际电磁转矩大于负载转矩，进而实现系统制动减速运行。图8(c)为电机定子电流的波形，PMSM定子电流三相对称，幅值在加减速阶段大于稳态阶段，其频率随转速的增大而增大，随转速的减小而减小。图8(d)为基于快速矢量选择FCS-MPC和枚举法的FCS-MPC下的逆变器输出线电压波形，包括加速、转矩阶跃及减速阶段的对比，可以看到2种控制下波形完全一致、控制效果相同。

图9为系统暂态运行时双向qZSI侧仿真结果。图9(a)为阻抗源网络的电感电流波形，可以看到直流侧功率随电机负载转矩和转速指令值的变化而变化。当转矩一定时，电感电流随着系统加速而增大，随着减速而减小；恒速运行时，电感电流保持不变。图9(b)为电源电压及电容电压，电容电压随着输入电压的变化而变化，以实现对直流链电压的跟踪控制。图9(c)为直流链电压波形，直流链电压幅值为360 V，且在输入电压、电机转速逐步变化及负载转矩突变时维持不变，几乎无超调。图9(d)为基于快速矢量选择FCS-MPC和枚举法的FCS-MPC下的的局部放大直流链电压波形，包括加速、转矩阶跃及减速阶段的对比，可以看到2种控制下波形完全一致、控制效果相同，表明2种控制方法的本质相同。

图9 系统暂态运行双向qZSI侧仿真结果

以上仿真结果表明，在暂态过程中所提FCS-MPC可使系统实现对给定值的无静差跟踪，具有良好的暂态性能。同时，与基于枚举法的FCS-MPC策略相比，在取得相同控制效果的情况下可以减小在线计算量。

4 结 语

本文提出一种适用于双向qZSI驱动PMSM系统的快速FCS-MPC策略。通过预测ST及NST状态下的电感电流，并引入子代价函数以选择是否插入ST状态，进而实现双向qZSI的升压控制。另外，在NST状态下，快速FCS-MPC仅需遍历4种开关状态对PMSM定子电流进行预测和代价函数计算，进而选择最优开关状态实现对其转矩和转速的控制。在取得和传统枚举FCS-MPC控制效果的同时，所提控制策略可以减小在线计算量。仿真结果表明了上述控制方法的正确性，系统具有良好的动、静态性能。