基于自适应LMS算法的空间光束快速精扫描跟踪控制方法

熊子珺，刘磊,*，杨鸿杰

1. 西北工业大学 航天学院，西安 710072 2. 陕西省空天飞行器设计重点实验室，西安 710072

1 引言

卫星光束控制技术广泛应用于航天领域，如激光测距、激光通信、对地遥感等方面[1-2]，尤其在包括量子通信[3]、空间大型干涉仪[4]、激光时频传递[5]、超远距离通信[6]等空间精密光学研究领域有广泛需求。如何实现光束指向的快速、准确控制是空间精密光学控制的重要研究内容。

中国“墨子号”量子科学实验卫星已成功实验双向量子通信。量子通信需要在超远距离上建立量子信道分发密钥[7]。建立超远距离通信首先要通过光束的大范围调整实现初始指向，其次依靠信标激光在捕获不确定扫描实现高精度捕获和对准实现光路闭环，扫描和跟踪的速度和精度影响通信链路建立效率和通信性能[8]。如量子通信最终要求激光精度跟踪在±0.7 mrad的范围内跟踪控制误差在±5 μrad[7]。在空间激光武器中，光束控制精度直接影响系统的作战使用效率和效果，必须对目标进行高精度扫描捕获、跟踪及瞄准[9]。

压电快摆镜因其谐振频率高、响应速度快、体积小、质量轻的特点，能够满足空间精密光学系统的光轴控制参数要求，因此被广泛应用于空间扫描、捕获、跟踪和瞄准[10]。如压电快摆镜被广泛用于光束控制系统，如与伺服电机结合组成两级复合轴控制系统，补偿伺服电机的高频小角度残差[11]。

压电系统固有的非线性迟滞、蠕变和漂移等动力学特性会对光轴指向控制精度产生不利的影响。现有的压电系统研究主要集中在对压电系统的非线性迟滞、蠕变建模及相关控制技术上。常用的控制方法有滑模控制、H∞控制、模糊控制、逆模型前馈控制等[12-14]，其控制器性能建立在对压电系统的精确建模和辨识上[12]。压电系统的迟滞和非迟滞动力学需要采用不同频率、不同振幅的输入信号进行逐步辨识，辨识的模型多且复杂[16-17]。

本文给出一种基于自适应LMS算法的压电快摆镜扫描控制技术，对于压电系统的不同动力学特性不需要分开辨识，采用同一N阶有限冲激响应(FIR)滤波器对压电系统整体进行辨识和表示，辨识过程简单、方便，且可调参数少，控制器易调节。

这种自适应方法可以利用前一时刻已得的滤波器参数的结果，自动调节当前时刻的滤波器参数，以适应信号和噪声未知的或随时间变化的特性，从而实现最优滤波。采用自适应滤波控制方法能有效抑制电机振动噪声及高频扰动，增强压电快摆镜的抖动抑制和扫描跟踪控制能力。

自适应LMS算法已用于光束抖动控制，Watkins等采用激光抖动控制实验平台探测测试光束抖动及快摆镜闭环抖动控制，自适应LMS控制方法优于线性二次高斯(LQR)控制及梯度自适应格型算法(GAL)[18]。但这些研究并没有对自适应LMS算法对光束的扫描跟踪控制进行深入探讨。

本文在文献[18]的研究基础上，对自适应LMS算法对空间光束的快摆镜跟踪控制展开研究，分析不同算法参数对快摆镜控制的影响程度。根据快摆镜高阶模型特点引入自适应LMS扫描控制算法和辨识方法，对已知的压电快摆镜动力学模型采用LMS估计算法进行了辨识，并采用辨识到的FIR滤波器模型进行了光束扫描跟踪仿真控制。并通过实验对压电快摆镜电压输入-输出进行辨识，采用自适应LMS控制方法对不同频率参考电压进行跟踪控制，验证自适应LMS方法的有效性。

2 自适应LMS扫描控制算法

LMS算法是一种自适应信号处理算法，是最陡下降法的改进算法，LMS算法通过沿性能曲面最陡方向向下进行迭代以搜索曲面最低点。自适应LMS滤波算法，是LMS算法在实际工程应用中产生的算法。

LMS算法采用N阶FIR滤波器来得到控制信号y(k)，并且最小化均方误差e(k)，如图1所示[19-20]。

图1 自适应LMS扫描控制算法Fig.1 Adaptive LMS scanning control algorithm

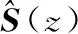
参考输入信号表示为：

X(k)=[x(k),x(k-1),…,x(k-N)]T

自适应滤波器W(k)表示为

W(k)=[w0(k),w1(k),…,wM(k)]T

因此，控制信号y(k)可以表示为：

WT(k)X(k)=XT(k)W(k)

压电快摆镜的动力学模型S(z)可表示为一个N阶FIR滤波器模型，即：

S(k)=[s0(k),s1(k),…,sN(k)]T

主动控制信号向量Y(k)表示为：

Y(k)=[y(k),y(k-1),…,y(k-N)]T

因此，压电快摆镜的转角为：

传感器测量得到的误差角可以表示为：

其中，d(k)=X(k)*P(z)。

因为参考输入信号x(k)和扰动信号d(k)是相关的，因此可以通过调节自适应滤波器W(k)来使得参与误差角e(k)最小。最小化目标函数定义为：

J=E[e2(k)]=min

LMS算法中采用平方误差代替均方误差，则性能曲面的梯度为：

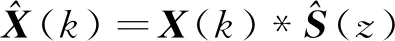
因此，通过逆梯度方向调节自适应滤波器W(k)的每一个滤波器系数，可以得到自适应LMS控制器为：

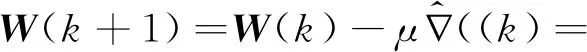
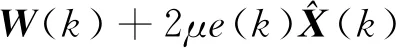
其中，自适应迭代步长μ为一个正数。μ的取值要求大于零且小于输入信号X(k)的自相关矩阵R的最大特征值的倒数[21]，即：

图2给出了辨识压电快摆镜模型的LMS估计算法框图。

图2 辨识压电快摆镜模型的LMS估计算法示意Fig.2 Schematic of LMS estimation algorithm for identifying piezoelectric steering mirror model

3 压电快摆镜扫描控制仿真

3.1 模型辨识

将文献[22]里的压电快摆镜模型作为参考模型，采用图2所示的LMS估计算法进行辨识。采用白噪声作为输入信号X(k)，对压电快摆镜进行辨识，步长0.000 5 s，图3为参考模型生成的100阶冲激响应系数，图4为采用LMS估计算法对参考模型进行辨识得到的100阶FIR滤波器，辨识到的系统模型与参考模型的开环输出误差可在10-10以下。

图3 参考模型FIR滤波器系数Fig.3 FIR filter coefficients of reference model

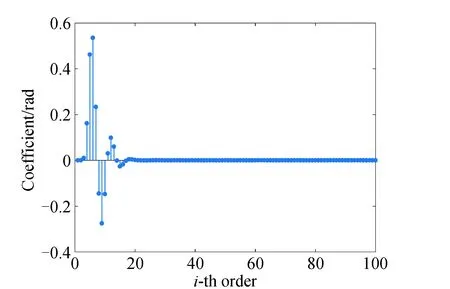
图4 LMS估计算法辨识到的FIR滤波器系数Fig.4 FIR filter coefficients identified by LMS estimation algorithm

3.2 扫描控制仿真

在压电快摆镜控制过程中，根据迭代步长范围要求式，选择μ=1 000。令压电快摆镜跟踪不同频率的参考角度(幅值均为1×10-4rad)，测量噪声服从正态分布N(0,1×10-14)。压电快摆镜对10 Hz、40 Hz及1 Hz与30 Hz复合的正弦信号的跟踪结果及误差分别如图5-图10所示，跟踪误差分别为0.31%(3σ)、0.30% (3σ)、0.46% (3σ)。仿真结果表明，基于自适应LMS算法的压电快摆镜控制对于高频及多频复合信号有良好的跟踪性能，但对多频复合信号的跟踪速度低于单频信号。

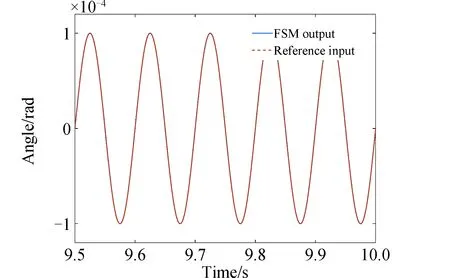
图5 10 Hz信号跟踪结果Fig.5 Tracking result of 10 Hz signal

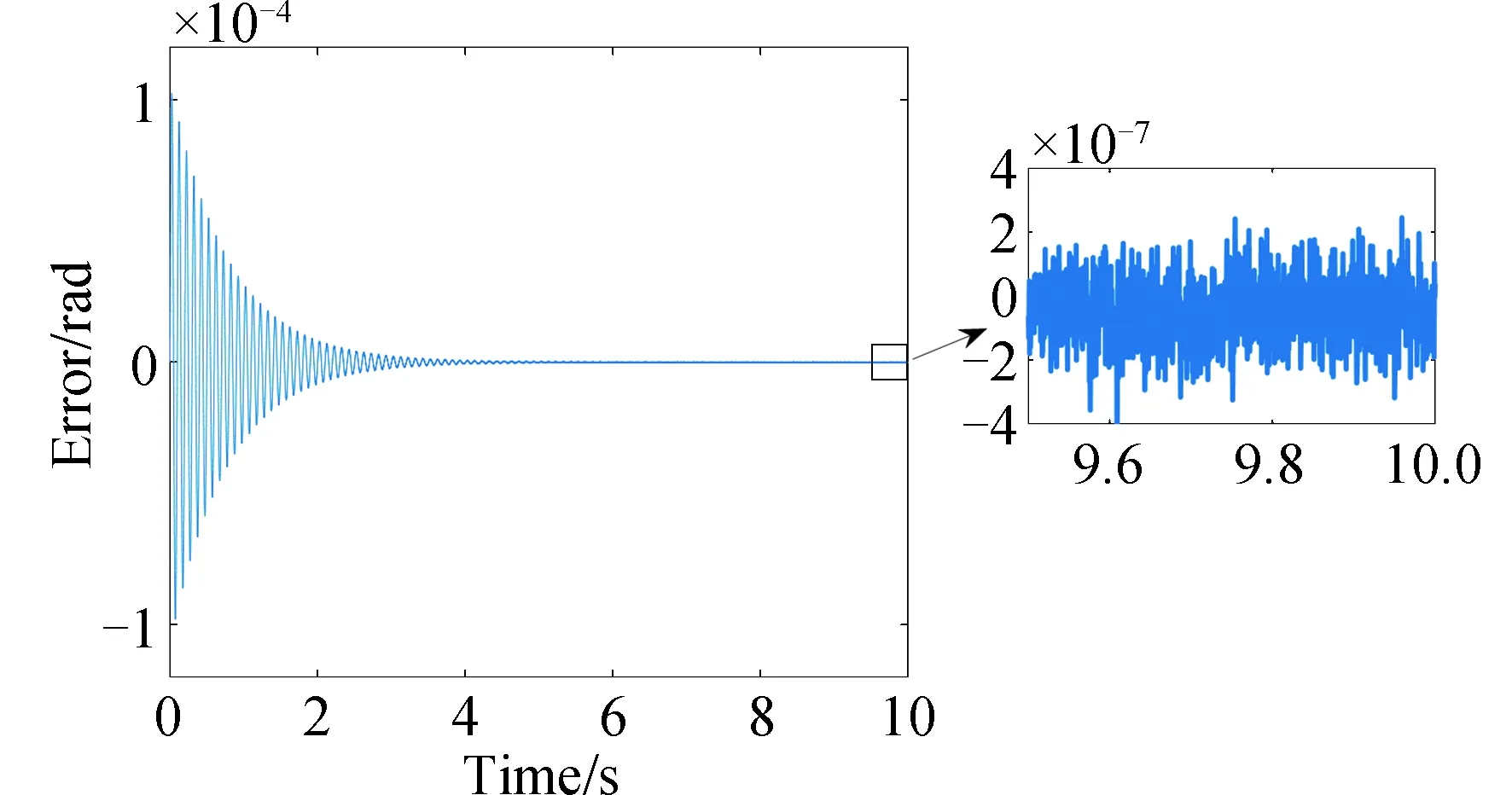
图6 10 Hz信号跟踪误差Fig.6 Tracking error of 10 Hz signal

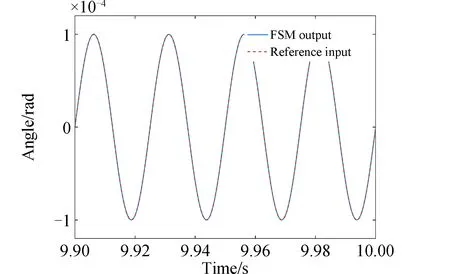
图7 40 Hz信号跟踪结果Fig.7 Tracking result of 10 Hz signal

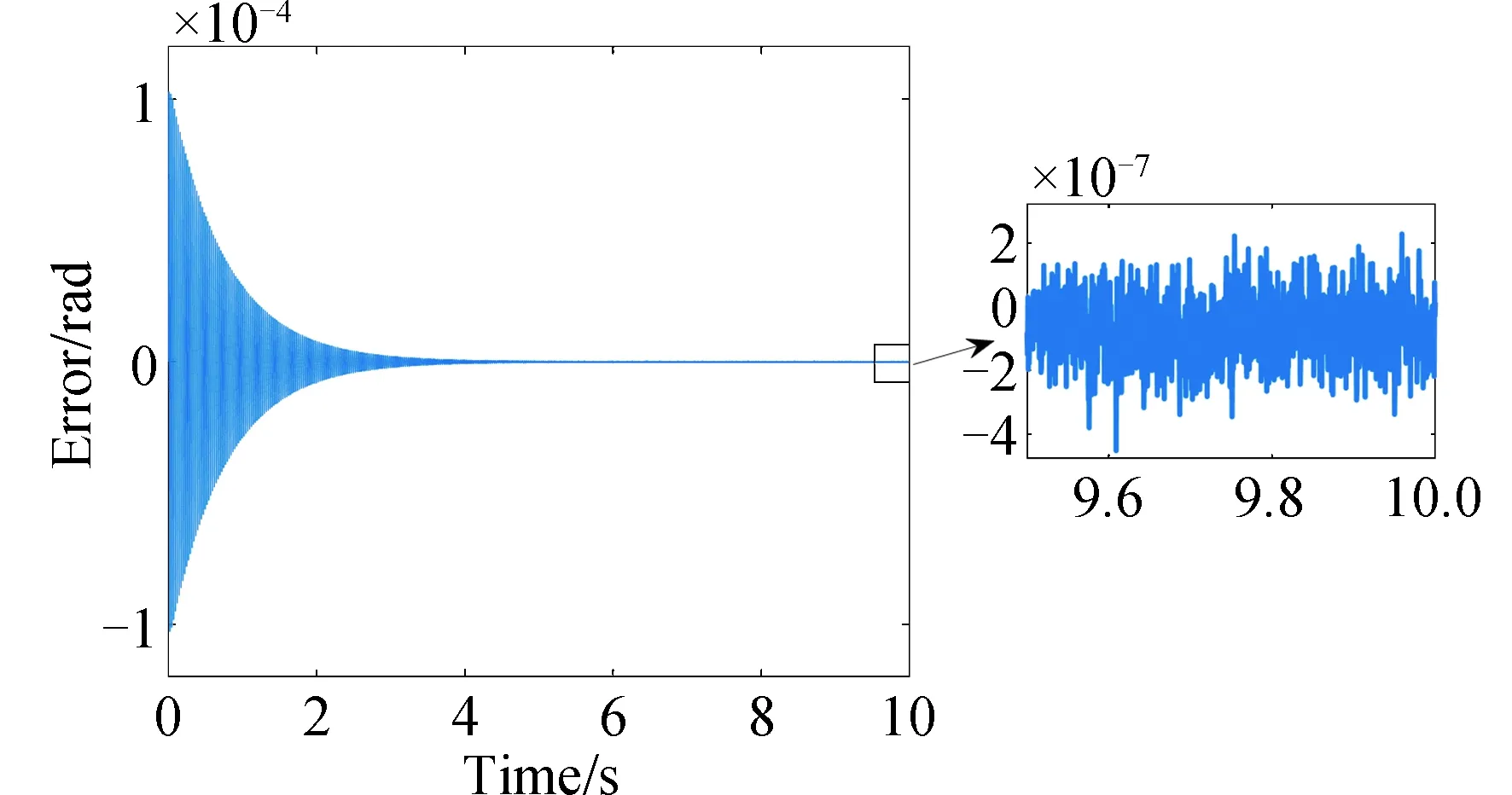
图8 40 Hz信号跟踪误差Fig.8 Tracking error of 40 Hz signal

图9 1 Hz、30 Hz复合信号跟踪结果Fig.9 Tracking result of 1 Hz and 30 Hz signal

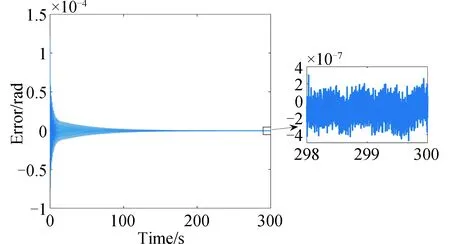
图10 1 Hz、30 Hz复合信号跟踪误差曲线Fig.10 Tracking error of 1 Hz and 30 Hz signal

不同频率下自适应LMS跟踪的收敛时间及跟踪误差对比如表1所示。其中，定义收敛时间为收敛到初始幅值的5%处的时间，除特殊说明外，μ=1 000。表1的对比结果说明：

表1 不同频率、不同迭代步长下收敛时间及跟踪误差对比

1)在同一μ值下，自适应LMS算法对10 Hz以下低频信号的跟踪收敛时间随频率增加而减少，对10 Hz以上高频信号的跟踪收敛时间与频率变化没有明显关系。

2)对10 Hz以下的低频信号，在式确定的迭代步长μ取值范围内，增加μ能有效减少收敛时间。

3)自适应LMS算法对于复合频率信号的跟踪收敛时间取决于复合信号中的较低频分量收敛速度，与较高频分量收敛速度无关。

4)不同频率信号及不同迭代步长μ对最终的跟踪误差没有明显影响，自适应LMS算法对不同频率的信号都能实现相同的跟踪性能。

4 压电快摆镜控制实验

4.1 实验设置及模型辨识

实验采用PI公司S-330.2SL型压电快摆镜及E509.S3型功率放大器，对压电快摆镜的x轴输出电压采用自适应LMS算法进行控制。

实验原理如图11所示，其中dSPACE实时控制系统用于生成参考信号Ur、产生控制信号uc以及对放大器输出信号进行带通滤波。带通滤波器用于过滤高频测量噪声及低频漂移。参考信号Ur在dSPACE实时控制系统中生成，并与滤波器输出信号Uf相减生成误差信号，经由控制器生成控制电压。控制电压经电压放大器放大后作用于压电快摆镜，电压放大器测量压电快摆镜的输出Uc并将其缩小输入dSPACE进行带通滤波。

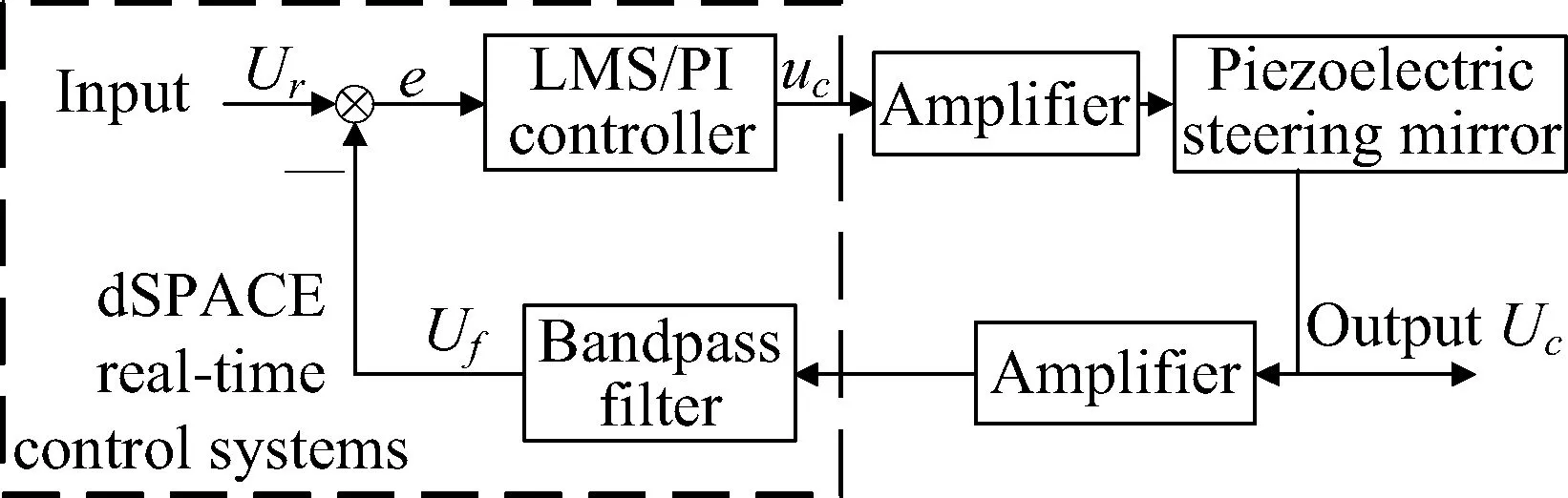
图11 压电快摆镜输入-输出跟踪控制实验原理Fig.11 Experimental principle of piezoelectric steering mirror input-output tracking control

首先，采用图2所示的LMS估计算法对压电快摆镜x轴从uc到Uf的模型进行辨识，辨识到的100阶FIR滤波器系数如图12所示。

图12 辨识压电快摆镜x轴得到的FIR滤波器系数Fig.12 FIR filter coefficients by identifying the axis x of piezoelectric fast steering mirror

辨识到的模型输出与快摆镜实际输出对比及误差分别如图13及图14所示，辨识误差为2.4%(3σ)。

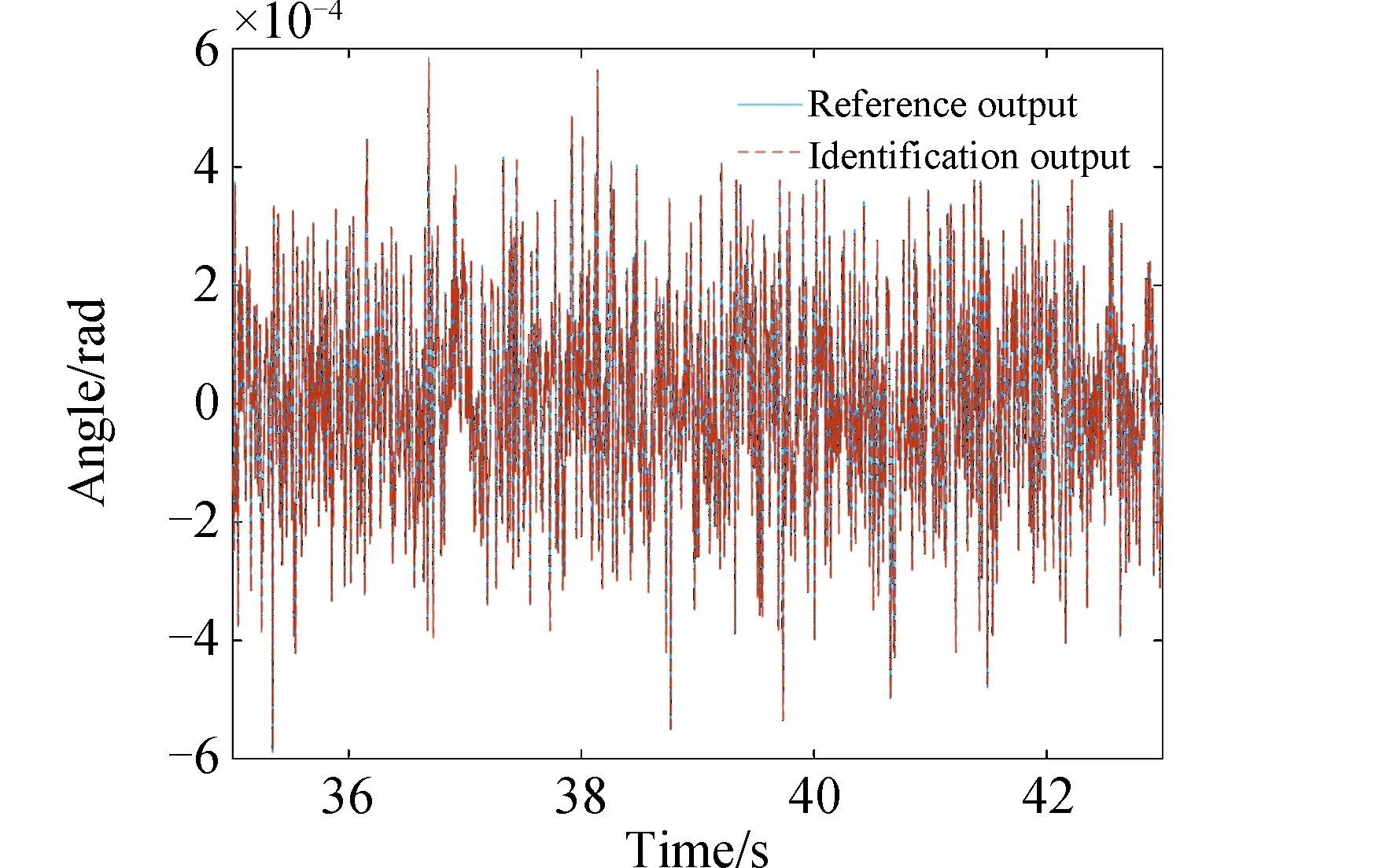
图13 辨识的模型与参考模型输出对比Fig.13 Output comparison between the identified model and reference model

图14 辨识的模型与参考模型输出误差Fig.14 Output errors between the identified model and reference model

4.2 实验结果

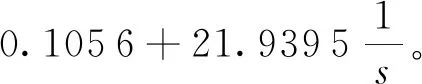
为防止高频信号下压电快摆镜失稳，实验分别对2 Hz和10 Hz参考角度跟踪效果进行了LMS控制及PI控制对比。图15和图16分别为对2 Hz谐波参考角度的LMS控制及PI控制输出对比及误差曲线，仿真结果表明，自适应LMS控制与参考输入相位差为1.41°，控制误差为2.5%(3σ)，PI控制与参考输入的相位差为4.86°，控制误差为8.4%(3σ)。

图15 2 Hz角度跟踪结果对比Fig.15 Tracking result comparison of 2 Hz signal

图16 2 Hz角度跟踪误差对比Fig.16 Tracking error comparison of 2 Hz signal

图17和图18分别为对10 Hz谐波参考角度的自适应LMS控制及PI控制输出对比及误差曲线，仿真结果表明，自适应LMS控制与参考输入相位差为1.06°，控制误差为1.9%(3σ)，PI控制与参考输入的相位差为21.35°，控制误差为36.4%(3σ)，跟踪10 Hz信号的自适应LMS控制误差低于PI控制的10%。从图17和图19可以看到，2 Hz的误差曲线在前0.2 s收敛很快，之后进行缓慢收敛，最终得到2 Hz的跟踪收敛时间为7.17 s，10 Hz的跟踪收敛时间为0.45 s，对10 Hz信号的跟踪收敛时间远小于2 Hz，符合仿真中的收敛时间差异。

图17 10 Hz角度跟踪结果对比Fig.17 Tracking result comparison of 10 Hz signal

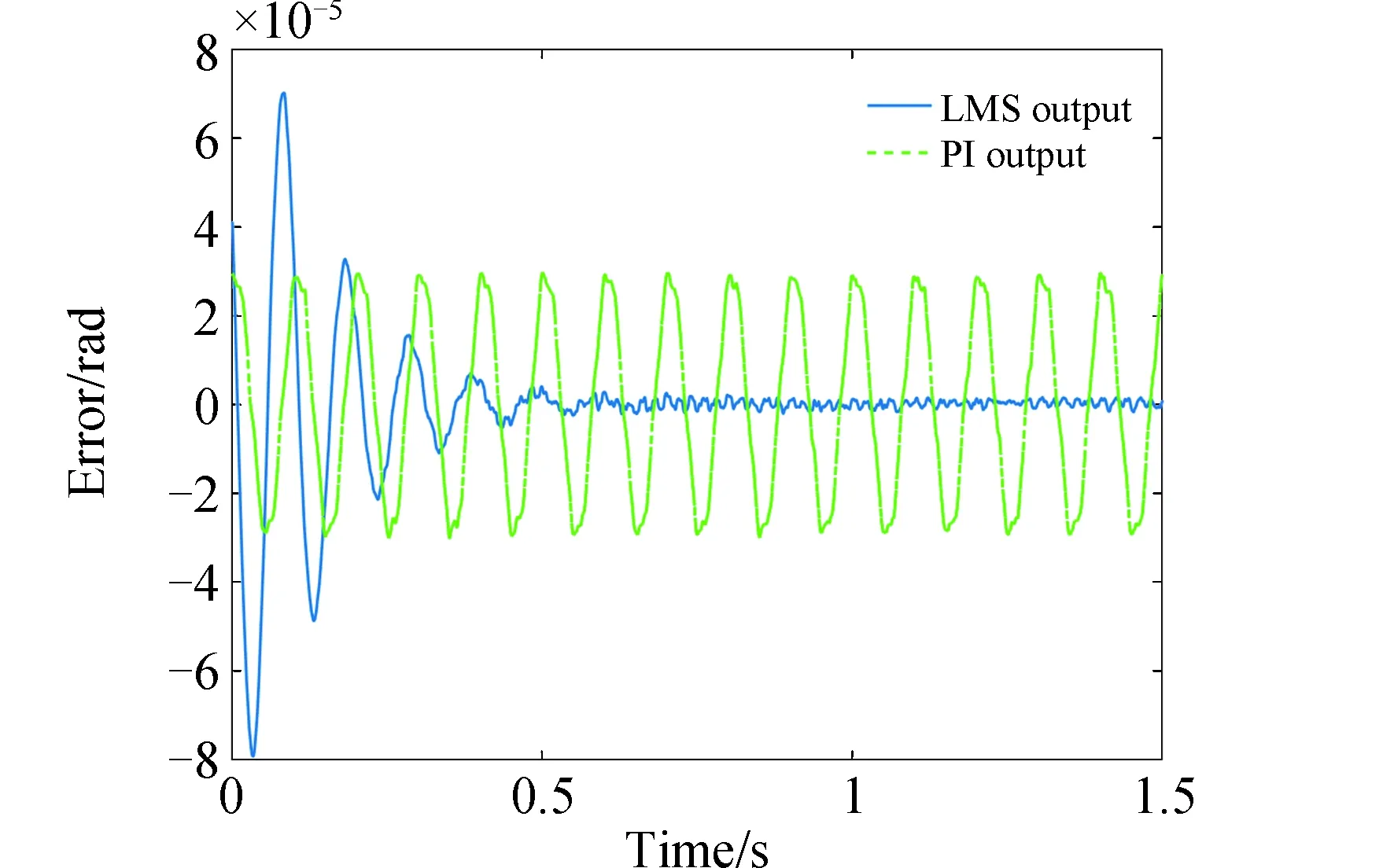
图18 10 Hz角度跟踪误差对比Fig.18 Tracking error comparison of 10 Hz signal

图19和图20分别为对2 Hz与10 Hz复合参考角度的自适应LMS控制及PI控制输出对比及误差曲线，仿真结果表明，自适应LMS控制与参考输入相位差为2.72°，控制误差为2.4%(3σ)，PI控制与参考输入的相位差为15.39°，控制误差为26.5%(3σ)，跟踪10 Hz信号的自适应LMS控制误差同样低于PI控制的10%。将实验结果总结在表2中。

图19 2 Hz、10 Hz复合角度跟踪结果对比Fig.19 Tracking result comparison of 2 Hz and 10 Hz signal

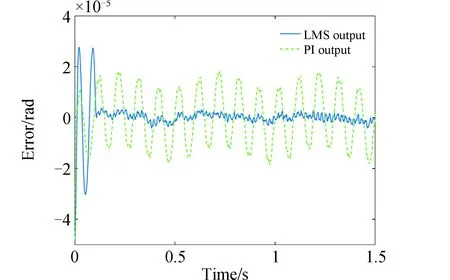
图20 2 Hz、10 Hz复合角度跟踪误差对比Fig.20 Tracking error comparison of 2 Hz and 10 Hz signal

表2 不同频率下自适应LMS算法与PI控制跟踪误差对比

5 结论

本文研究了基于自适应LMS算法的压电快摆镜空间光束扫描跟踪控制技术。首先给出了自适应LMS扫描控制算法和辨识方法，并仿真研究了不同频率和不同迭代步长下自适应LMS算法的光束跟踪控制精度。仿真结果表明在适当范围内改变频率和迭代步长只能改变自适应LMS控制的扫描收敛时间，并不影响最终控制的扫描精度。最后采用实验对未知压电快摆镜进行了自适应LMS辨识，利用辨识得到的100阶FIR滤波器模型设计了自适应LMS算法，对目标快摆镜进行了输入-输出扫描跟踪控制，实验结果表明自适应LMS算法对2 Hz和10 Hz及他们的复合信号的跟踪误差分别为2.5%(3σ)、1.9% (3σ)和2.4%(3σ)，均优于PI控制算法，说明自适应LMS对多频参考信号有很好的跟踪效果。