超大口径环形天线包带展开过程动力学仿真
2021-10-26胡建峰杨军刚肖勇万小平冯涛王勇郑冰
胡建峰,杨军刚,肖勇,万小平,冯涛,王勇,郑冰
1. 中国空间技术研究院西安分院,西安 710100 2. 西安嘉业航空科技有限公司,西安 710089
1 引言
环形可展开天线[1-2](见图1)以其高收纳比、轻质量等特点,已成为国内外超大口径天线研究的主流结构形式。
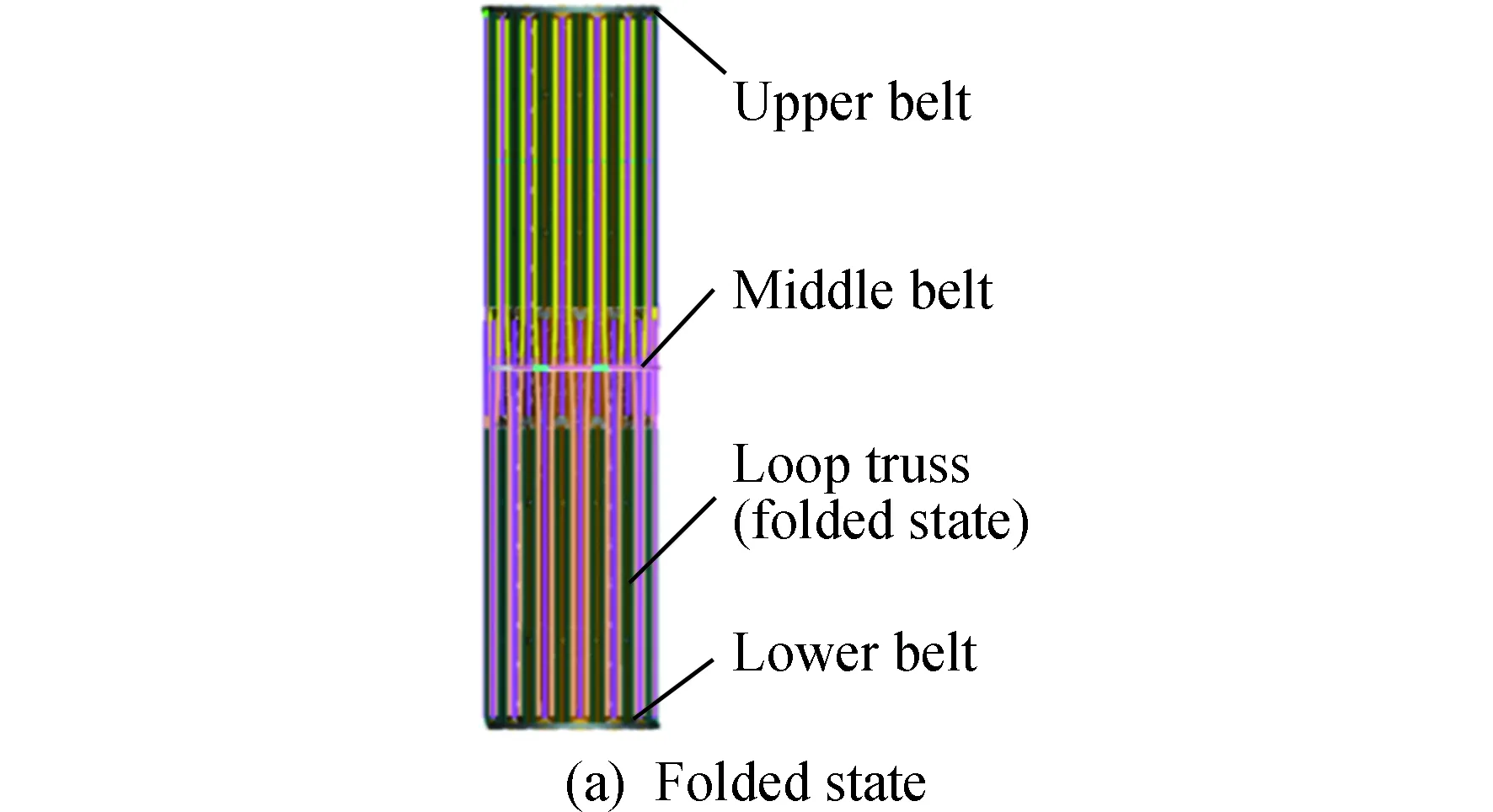

图1 环形可展开天线结构示意Fig.1 Loop antenna sketch map
中间包带是环形可展开天线的重要组成部分,其功能为实现环形可展开天线收拢状态紧固及展开状态按指令解锁释放,它主要由复材包带、根部固定端、逆止回弹机构、拔销器、金属接头等组成,如图2所示。因中间包带展开过程与环形桁架展开同步进行,且复材包带为轻质、大柔性部件,地面试验难以模拟在轨零重力展开过程。此外,当环形可展开天线口径增大至30 m及以上时,反射器同步铰链初始力矩增大,导致桁架预展速度增大;天线口径增大导致相应复材带长度增大,收拢时弹性势能增大;这两种因素导致超大口径环形天线展开过程中金属接头与桁架管件存在很大碰撞风险。因此采用数值仿真方法对在轨展开真实情况预示以及通过仿真识别敏感性要素进而提高展开可靠度具有重要意义。

图2 中间包带组成示意Fig.2 The composition of middle flexible belt
在针对大变形及大范围运动柔性部件建模方面,目前主流方向包括绝对节点坐标法[3-4]和几何精确梁理论[5-8]。文献[9]基于绝对节点坐标法对环形天线展开不同步性进行分析,文献[10]基于几何精确梁理论对环形天线进行动力学建模仿真。以上两种建模方法在计算效率、解决奇异性、应变客观性、编程实现等方面各有优缺点[11]。在编程方面绝对节点坐标法更易实现,但在精度和计算速度方面,几何精确法更占优势。
本文针对30m环形天线包带展开过程采用柔性多体动力学理论对运动过程出现大变形的柔性复材带建模、变形较小的金属部件建模、各部件之间约束建模以及拔销器爆炸产生的冲击及复材包带和桁架管件接触建模,从而实现对超大口径环形天线柔性包带展开过程动力学建模。在此基础上对桁架预展速度、复材带阻尼率对复材带金属接头和周边桁架最小距离影响分析;考虑在轨极端条件下,逆止回弹机构失效时金属接头和薄壁管件之间碰撞情况进行分析。
2 系统描述及动力学建模
2.1 系统描述
天线展开时,中间包带拔销器解锁释放,复材包带在弯曲变形和预紧力作用储存的弹性势能作用下以根部固定端为轴进行旋转,当复材包带根部旋转至固定端限位面时,因固定端面限位作用,复材包带根部无法继续向前旋转,同时逆止回弹机构作用,包带根部无法向后旋转,复材包带根部无法旋转;因复材包带柔性较强、长度较长原因,依然会绕根部固定端进行回弹;在中间包带展开同时,环形桁架在自身驱动铰链作用下逐渐展开;环形桁架和中间包带同步展开过程如图3(a)(b)所示。
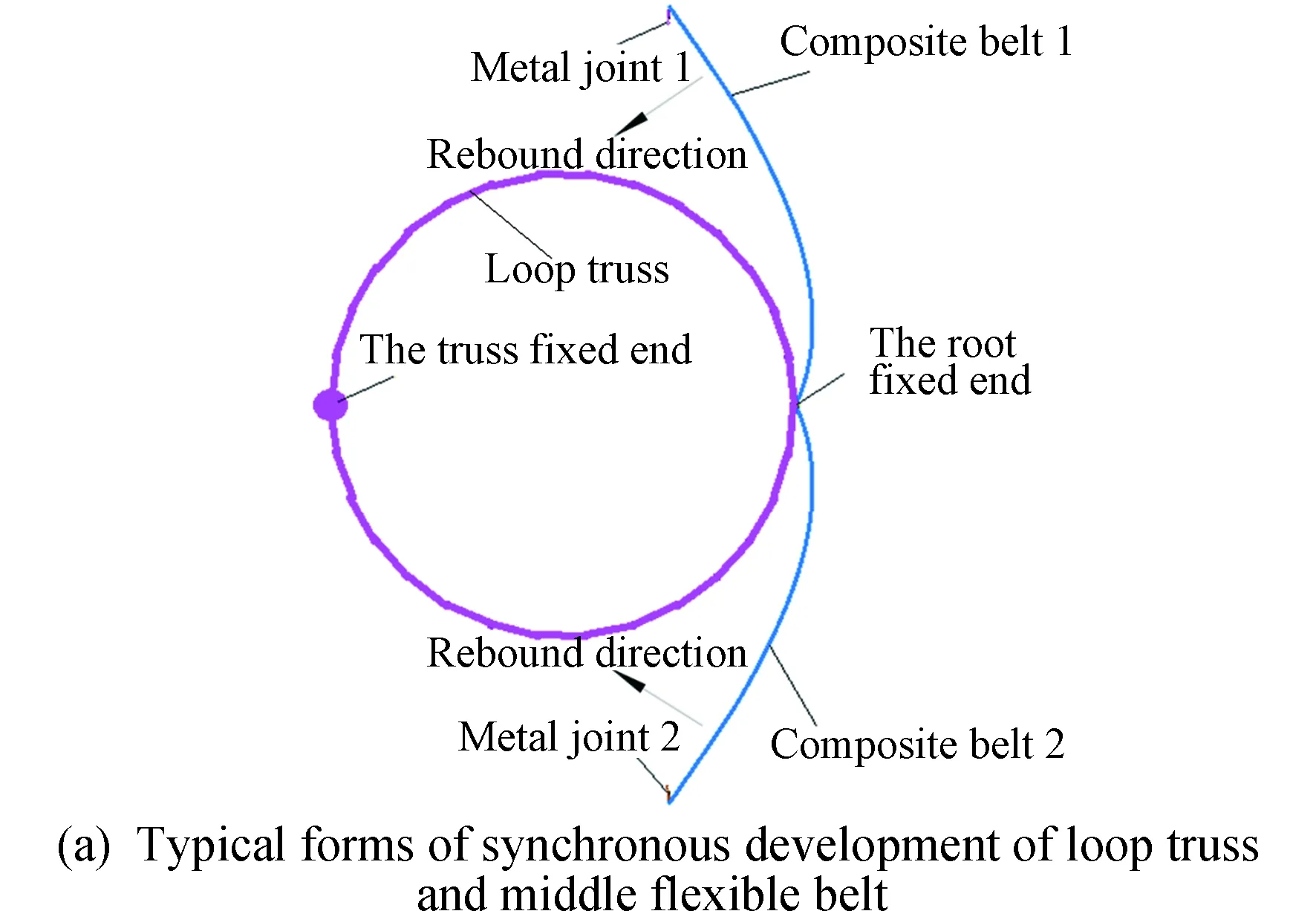
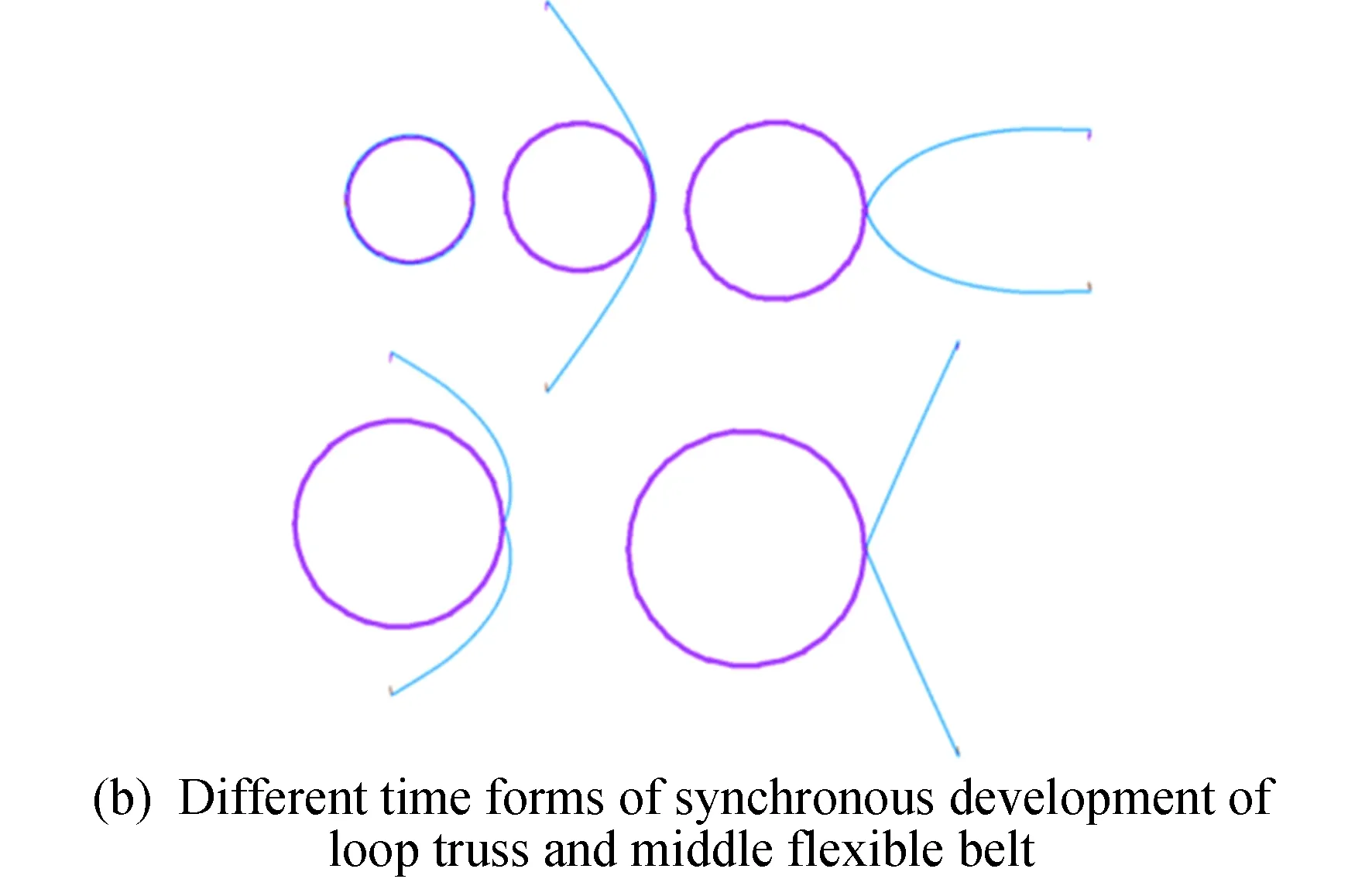
图3 环形桁架和中间包带同步展开过程示意Fig.3 Synchronous development process of loop truss and middle flexible belt
在柔性多体动力学研究过程中通常采用第一类拉格朗日方程作为系统动力学控制方程:
(1)
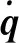
2.2 金属部件建模
对于超大型口径天线包带展开过程动力学建模,研究过程中通常把变形极小的部件固定座和金属接头当作刚体处理。刚体在三维空间运动可分解为3个方向平动和3个方向转动,每个刚体具有6个自由度。在选取广义坐标方面,采用刚体质心位置确定平动构型;关于转动的描述,在文献[12]中有很多种,本文选用转动向量法来描述刚体转动。根据欧拉转动定理和转动向量的定义[12]:转动向量φ与转动轴a平行,且模与转动角相等。转动向量φ到旋转矩阵A的转换关系为:
(2)
式中:I为三维单位阵;h1、h2均是转动角φ的函数,

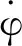

(3)
(4)
其中:
(5)
进一步可以证明:
HT=ATH
(6)
最终可以得到:
(7)
考虑到刚体没有弹性势能项,则式(1)可简化为:
(8)
其中q=[riφi]。 式(8)中动能表达式为:
(9)
式中:J为质心坐标系下转动惯量。
2.3 柔性复材带建模
柔性包带展开过程中会发生大变形和大范围转动。根据几何精确梁理论,任意发生大变形和大范围转动的梁单元,其截面曲率均为几何精确,因此采用几何精确量理论对柔性包带建模相较于传统有限元方法建模更为精确。本文采用几何精确量理论对柔性包带建模;建模过程中,选取梁单元左右两端中心线位置r和转动向量φ作为广义坐标描述梁单元构型,如图4所示。
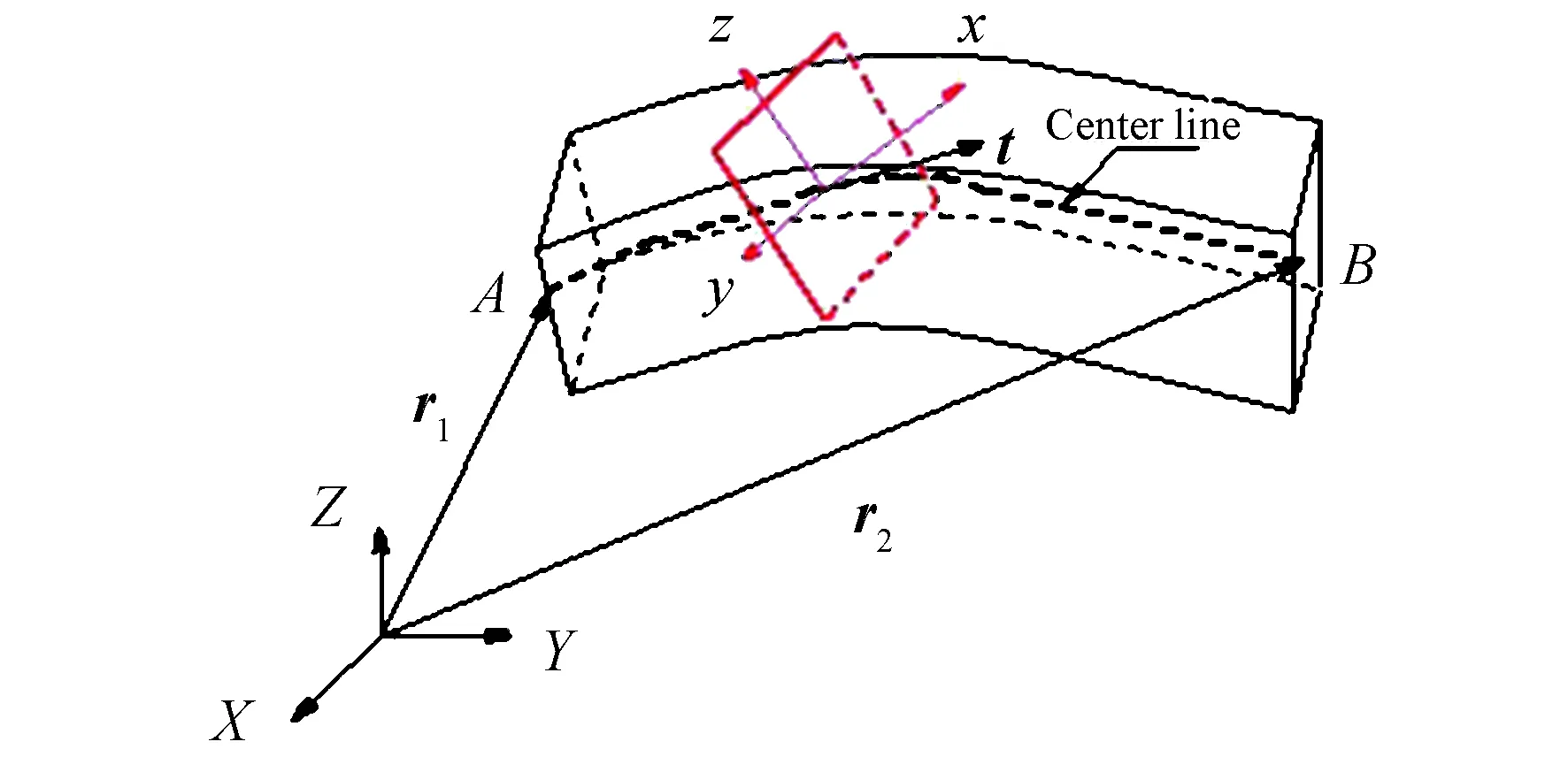
图4 柔性梁单元描述Fig.4 Flexible beam element sketch
梁单元的广义坐标可表示为:
在转动向量φ的插值处理方面, 文献[13]提出在梁单元内建立一个参考坐标系,并在参考坐标系下对转动向量进行插值计算,基于此计算得到的曲率因为整体去掉了参考坐标系影响,在任何观测坐标系均可得到相同曲率。本文对于转动向量插值也按此方法进行。任意一点相对参考坐标系转动向量记为φr。根据上述,梁单元内中心线任意一点r、φr有如下表达:
(10)
式中:ξ∈[0,1]为梁单元内参数坐标。梁单元动能可表达为:
(11)
式中:L为梁单元长度;A为单元横截面积。
梁单元势能可表达为:
(12)
其中:
γ=ATr′
κ=HTφ′
N=CN(γ-γ0)
M=CM(κ-κ0)
式中:γ为应变向量;γ0为初始应变向量;κ为曲率向量;κ0为初始曲率向量;N和M分别为截面力和力矩,上述物理量均可用广义坐标表达;CN和CM为仅和材料及截面特性相关的本构矩阵。
对于柔性包带初始预变形情况,其在预紧力作用下,整个包带会沿截面方向进行一定拉伸。轴向初始拉伸总应变量为:
εL0=F/EA
(13)
式中:F为包带预紧力;E为杨氏模量。
各单元初始拉伸预应变为1/NεL0,其中N为柔性梁单元数,包带收拢时梁单元剪切向量近似于零,可忽略不计。初始曲率向量κ0可通过初始姿态曲率对弧长求导获得。
2.4 桁架建模
周边桁架在预展过程中,和转接臂固连的竖杆固定不动,且预展过程各个竖杆从俯视往下看始终保持圆形,如图5所示。

图5 预展过程桁架展开示意Fig.5 The loop truss deploying sketch
考虑到展开过程包带金属接头和横杆及斜杆不存在碰撞,因此在建模过程根据工程实际经验,令固定端竖杆坐标P0(0,0,0)、反射器远端竖杆坐标为PN/2(2f(t),0,0);则任意竖杆任意时刻位置可表达为Pi=(f(t)cos (i·θ)+f(t),f(t)sin (i·θ),0),i为竖杆编号,θ为各边圆心角,其中f(t)为任意时刻圆心运动方程。任意时刻竖杆i运动方向为(f(t)cos (i·θ)+f(t),f(t)sin (i·θ),0)。
2.5 约束建模
柔性包带固定座和竖杆存在固定约束,柔性包带根部和固定座存在旋转约束;关于约束部分建模可参见文献[14]描述的建模方法。
2.6 接触碰撞建模
包带展开过程中,柔性包带和桁架竖杆存在接触碰撞,如图6所示。
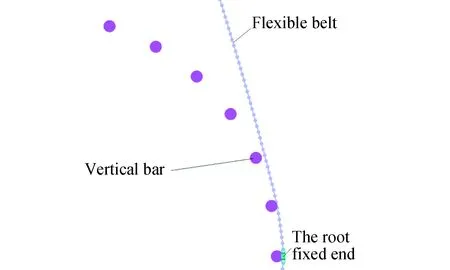
图6 复材包带和桁架竖杆接触示意Fig.6 Contact between composite belt and loop truss vertical bar
本文采用文献[15]提出的非线性弹簧阻尼模型来描述碰撞力。在研究过程中柔性包带和竖杆的碰撞可以表示为柔性包带任意单元点是否和竖杆外轮廓曲线发生嵌入。在非线性阻尼弹簧模型中,碰撞点和碰撞曲线在接触点处外法向弹力FN可表达为:
(14)
式中:K为接触刚度;s为嵌入深度,上标e是弹簧非线性指数;c为阻尼系数。此外接触点还存在切向摩擦力Fμ作用,其计算方法可参看文献[15-16]。通过虚位移原理将法向及切向接触力在广义坐标下进行表达并带入系统动力学控制方程组(1)求解。
2.7 冲击建模
包带拔销器解锁时,炸药爆炸在te时间内对金属接头形成Fe的推力。根据虚位移原理:
(15)
则拔销器对金属接头推力Fe在广义坐标下可表达为:
(16)
2.8 逆止回弹机构建模
包带展开过程中,当包带根部转动到极限角度后,包带固定座会对包带根部产生限位作用,使其无法继续向前转动;此时包带根部棘轮棘爪装置作用,使包带根部无法向后转动。建模过程中,对于包带根部逆止回弹,可以对根部转动角进行约束控制:
ωmz=0, ifφmz=θmax
(17)
2.9 小结
本节通过采用几何精确梁理论对复材包带建模、多刚体动力学理论对变形极小部件和约束建模、非线性弹簧阻尼模型对接触碰撞进行描述以及虚位移原理将空间力(力矩)转化为广义坐标下广义力等方法,利用数值编程求解多体动力学方程组,实现30 m环形天线包带展开过程动力学仿真。
3 仿真及参数敏感性分析
通过上述建模仿真,可以得到30 m环形天线包带和桁架同步展开过程,包带金属接头到桁架竖杆最小距离变化曲线,如图7所示。随着包带展开,金属接头和周边桁架距离开始变大,当复材包带在回弹时,距离开始变小,直到距离最小;随后逐渐振荡直至稳定;通过地面试验和仿真分析,包带第一次回弹金属接头到周边桁架距离最小。对于包带阻尼率0.04、周边桁架1倍标准速度下,金属接头第一次回弹距周边桁架最小距离为402 mm。
通过仿真分析发现,复材带阻尼率对金属接头与周边桁架展开过程最小距离有重要影响,且满足阻尼率越大,金属接头与周边桁架展开过程最小距离越大,如图8所示。
图8 金属接头与周边桁架最小距离和复材包带阻尼率变化规律Fig.8 The minimum distance between metal joint and loop truss changes with the damping rate of belt material
通过仿真分析,环形桁架预展速度对金属接头与周边桁架展开过程最小距离有重要影响;且满足如下规律:桁架预展速度越大,金属接头与周边桁架展开过程最小距离越小,如图9所示。

图9 金属接头与周边桁架最小距离和桁架预展速度变化规律Fig.9 The minimum distance between the metal joint and the loop truss changes with the velocity of the truss
4 极端条件分析
中间包带在轨展开最恶劣的情况为逆止回弹机构失效,即止回弹机构无法限制包带根部回弹。考虑到在轨无重力影响,环形桁架展开速度较地面偏大,假设桁架预展速度为1.2倍标准速度,结合目前复材带阻尼率0.04,对包带在逆止回弹机构失效条件进行仿真,仿真结果如图10所示,最小距离仅为121 mm。
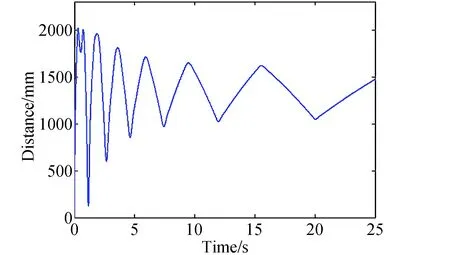
图10 在轨棘轮失效条件下金属接头与周边桁架最小距离变化规律Fig.10 The minimum distance between metal joint and loop truss under failure condition of ratchet device
5 结论
环形天线中间包带在轨展开过程,地面目前尚无有效方法对其进行遥测观察,主要采用柔性多体动力学建模仿真结合在轨及地面试验数据对在轨展开进行预示。本文基于仿真分析得出,对包带金属接头到桁架最小距离影响较大因素主要为复材带结构阻尼率和桁架预展速度:复材带阻尼率越大,金属接头与桁架最小距离越大;预展速度越大,金属接头与桁架最小距离越小。在包带设计过程中,为了提高包带展开可靠性,减小金属接头和薄壁复材管件碰撞风险,可以通过提高复材带阻尼率和减少桁架预展速度方式来增大展开过程金属接头到桁架最小距离。此外,通过对在轨逆止回弹机构失效模式进行分析,逆止回弹机构失效条件下金属接头到桁架最小距离仅为正常条件约30%,金属接头和薄壁复材管件碰撞风险大大增加。因此,在包带设计及加工过程中,应提高逆止回弹机构可靠性,避免出现失效模式。
