含非线性特性的卫星压紧释放机构动力学研究
2021-10-26刘汉武张华方贤亮
刘汉武,张华,方贤亮
1. 上海宇航系统工程研究所,上海 201109 2. 上海市空间飞行器机构重点实验室,上海 201109
1 引言
压紧释放机构作为空间机构重要的连接结构,完成空间机构在发射过程中的固支压紧作用,同时通过火工品爆炸的方式解除锁定,从而释放空间机构,其在航天上应用非常广泛,例如太阳翼、天线、空间结构机构等,随着航天器结构机构越来越复杂,压紧释放机构也发展出了新的构型(见图1),该新型压紧释放机构采用C型抱爪进行收拢压紧,其中存在限位、抱紧力及摩擦力等非线性因素,该部件对天线的动力学特性起关键作用,故其中的非线性因素对天线动力学特性不可忽视。通常大型复杂航天器结构由若干次级结构或子结构通过类似的各种连接结构组合而成,其中的连接结构大多都伴随有各类非线性问题。例如:航天器的铰接结构[1-3]、大型航天器的伸展结构[4-8]、运载火箭的包带连接机构[9-11]等此类航天器连接结构中存在各类非线性因素,正如上述提到的典型结构机构一样,具有明显的局部性和离散性特点,如何对含有非线性特征的结构进行动力学分析是亟需解决的问题。
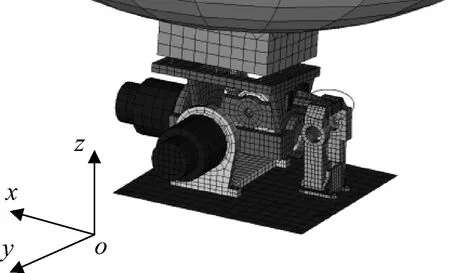
图1 卫星天线新型压紧释放机构Fig.1 A new type of hold-down and release mechanism for satellite antenna
针对结构的非线性问题,国内外许多学者,王天舒等[12]采用分段线性模型研究了航天器附件展开过程中间隙非线性的影响;徐小胜等[13]推导了柔性飞行器系统的模态频率估算公式,结合有限元软件建立了一种粗略研究柔性航天器频率的工程方法;徐超等[14]将改进 Iwan 模型用于构造非线性连接元对螺栓连接梁的非线性动力学响应进行了分析,该模型能够反映连接界面在不同载荷幅值下的复杂的粘着-滑动行为特征,以及幅变非线性阻尼的特征;Song[15]将改进的Iwan 模型扩展成三维单元,并采用神经网络方法对一个含有螺栓连接的梁结构进行了参数识别。豆博等[16]考虑了摩擦模型对空间抓捕过程中的碰撞分析模型进行了修正,研究了碰撞摩擦等非线性特性对空间抓捕的影响;韩雪艳等[17]采用牛顿-欧拉法对含间隙、摩擦磨损等非线性因素的二维指向机构的动力学特性进行了研究;危清清等[18]考虑了空间对接机构的接触碰撞等非线性特性,对机械臂辅助舱段对接动力学进行了仿真研究。这些研究仅是针对较为简单的梁模型等,或者是对系统频率进行粗略估算,无法较为合理描述复杂的相关连接关系,故本文提出了一种非线性分析方法——等效刚度区间法,该方法需要建立局部结构模型,考虑局部结构的非线性特性,通过理论方式加载得到局部非线性结构的力-位移曲线,根据实际结构的工作区间对结构刚度进行取值,得到局部结构等效刚度区间,最后将该值代入模型即可进行结构动力学特性分析。
2 建立模型
对于一个非线性多自由度系统,其控制方程可以表示为:

(1)
式中:M、C和K分别为系统的质量、阻尼和刚度矩阵;zj(t)为非线性函数向量;Aj为非线性函数的系数。将方程两端同时进行傅里叶变换并加以整理得到:
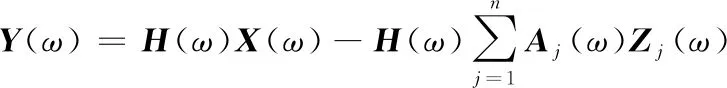
(2)
式中:H(ω)是隐含线性系统的导纳矩阵,如果系统的激励X(ω)和响应Y(ω)可由试验测量得到,则可以利用式(2)对参数A1(ω),A2(ω),…进行识别。
由于含有非线性系统的刚度在动态过程中是时刻变化的,同时其等效刚度识别需要有试验支持,使得动力学分析失去了预示效果,于是本文提出对局部的非线性结构进行静力加载识别,能够识别出非线性结构的刚度区间,即参数A1(ω),A2(ω),…的取值区间。


图2 C型抱爪接触模型Fig.2 Type C gripper contact model

(3)
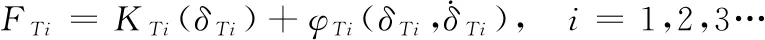
(4)
式中:函数KNi、KTi描述接触面的切向、法向刚度;函数φNi、φTi描述接触面的切向、法向阻尼特性, 它们都与接触的几何特征、材料特性相关;
接触力函数(3)和(4)是非线性的,根据经典的库仑摩擦模型,切向力满足:
FTi≤μFNi
(5)
在振动过程中压紧释放机构的C型抱爪是一个动态过程,主要由滑动摩擦系数起作用,约定C型抱爪间的材料静摩擦系数为μ0,则滑动摩擦系数μi可以表征为:

(6)

对于接触静止模式:
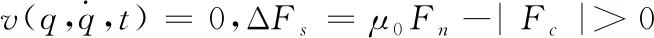
(7)
对于接触滑移模式:

(8)

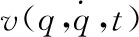
3 非线性刚度识别
复杂接触局部结构如图3所示,采用静力加载对其非线性刚度进行识别,对压紧释放机构分别单独施加六个方向载荷:Tx、Ty、Tz、Rx、Ry、Rz(Tx:x方向力;Ty:y方向力;Tz:z方向力;Rx:x方向力矩;Ry:y方向力矩;Rz:z方向力矩),得到各方向力(或力矩)-位移曲线,典型曲线见图4。
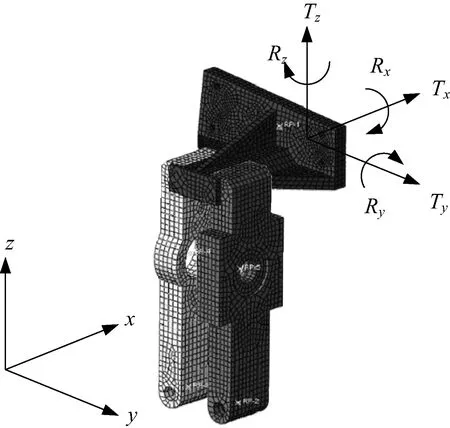
图3 局部结构非线性模型及加载坐标Fig.3 Nonlinear model of local structure and loading coordinates

图4 局部结构力-位移曲线对比Fig.4 Comparison of local structural force-displacement curves
由图4可以看出,非线性结构的弹性系数比线性结构弹性系数小很多,同时非线性结构的弹性系数呈现非线性特性,非线性结构中随着载荷的加大,结构弹性系数会出现变化,这是由于非线性结构中接触碰撞的区域出现了相对滑动,导致结构弹性系数出现变化,在载荷不大的情况下,弹性系数变化也不大,随着载荷的增加,弹性系数急剧减小,当载荷超过一个极限值时,此时弹性系数为零,说明非线性结构已经变成可活动的机构,无法继续承载,非线性结构局部弹性系数的变化类似于材料的拉伸曲线,都有一个类似塑性变形以及破坏的现象,我们可以引入材料中塑性极限和破坏极限的概念,将其应用在非线性结构中,可称其为“承载极限(Gb)”(见图5、图6)。
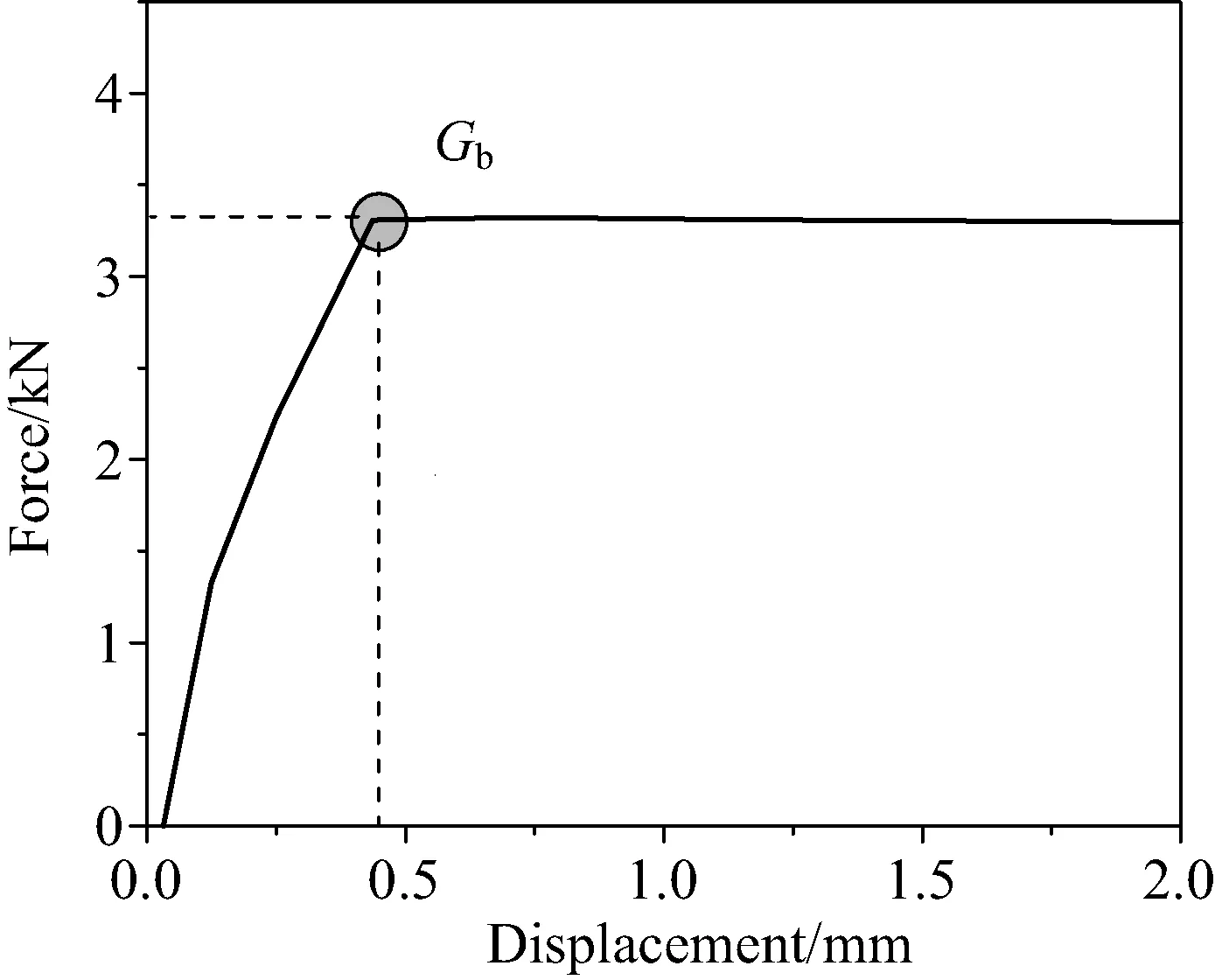
图5 非线性结构力-位移曲线Fig.5 Force-displacement curve of nonlinear structure
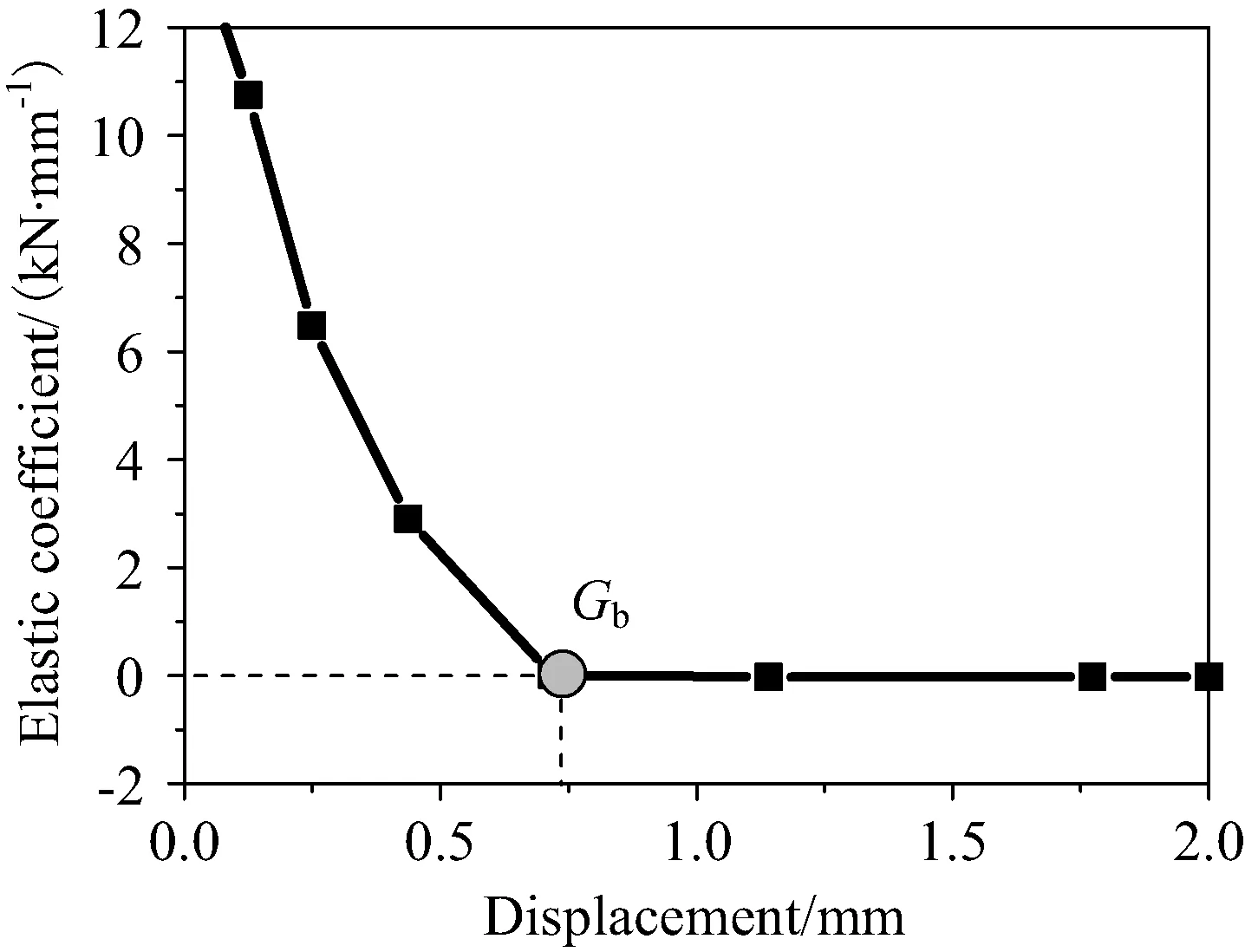
图6 位移与弹性系数的关Fig.6 Relation between displacement and stiffness
当载荷在“承载极限”以内时,在结构上施加反向载荷可以将结构恢复,但当载荷超过“过载极限”后,结构进入了一种不可逆的形式,即使施加反向载荷,结构也不会恢复,在结构设计过程中应当避免非线性结构在过载极限状态下工作。
局部非线性结构的载荷大小直接影响局部结构的刚度,这是与线性结构不同的,获得结构工作载荷是进行刚度选取非常重要的一步,压紧释放机构的工作载荷在一定的范围内,局部非线性结构的刚度选取依据以下原则:
(1)结构工作载荷范围限制原则
结构工作载荷在一定的范围内,结构刚度的选取依据工作载荷的大小,范围不会超出结构工作载荷。
(2)结构位移限制原则
对于多个局部非线性结构,也要同时考虑结构位移限制条件,以载荷和位移先到为止为原则。
分析压紧释放机构的最大工作载荷为Fmax=2 200 N,载荷区间为[0 N,2 200 N],最大位移为Dmax=0.25 mm,x向和y向弹性系数可以通过最大载荷力(Fmax)或者最大位移(Dmax)在图7、图8中选取。
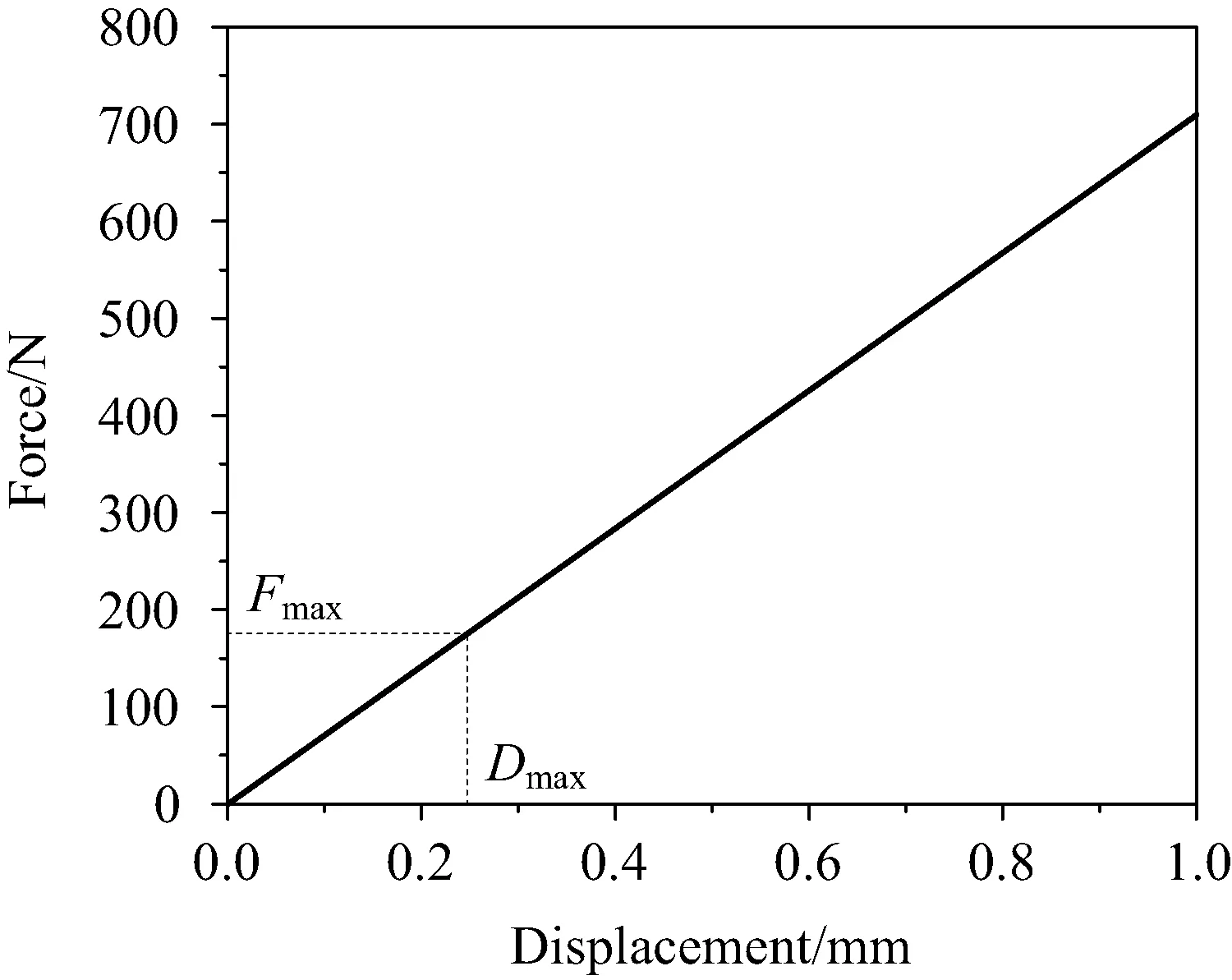
图7 Tx力-位移曲线Fig.7 Txforce-displacement curve

图8 Ty力-位移曲线Fig.8 Tyforce-displacement curve
z向弹性系数取值由于z向的试验量级与x、y向相比较高,约1.5倍,故最大工作载荷为:
F=2 200 N×1.5=3 300 N
最大位移Dmax=0.2 mm,非线性结构长度为Lx=186.4 mm,Ly=186.4 mm,Lz=30 mm,sinRxmax=Dmax/Lx,其中Rxmax为0.1,故Rxmax≈Dmax/Lx,Rymax≈Dmax/Ly,Rzmax≈Dmax/Lz。可得最大角为:
Rxmax≈arcsin(Dmax/Lx)=0.001 rad;
Rymax≈arcsin(Dmax/Ly)=0.001 rad;
Rzmax≈arcsin(Dmax/Lz)=0.01 rad。
可在其力-位移曲线图(见图9~图12)中通过Rmax选取弹性系数。
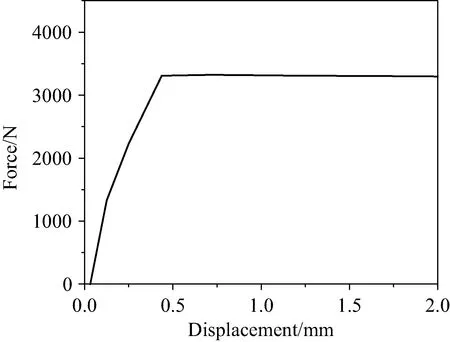
图9 Tz力-位移曲线Fig.9 Tzforce-displacement curve

图10 Rx力矩-位移曲线Fig.10 Rxmoment-rotation curve

图11 Ry力矩-位移曲线Fig.11 Rymoment-rotation curve

图12 Rz力矩-位移曲线Fig.12 Rzmoment-rotation curve
基于以上两项原则,得到压紧释放机构刚度取值区间(见表1),其中Px,Py,Pz为平动刚度,Mx,My,Mz为转动刚度。
由表1可知压紧释放机构弹性系数的取值区间,要确定天线的频率范围,需要根据压紧释放机构弹性系数取值区间对天线频率进行不确定性分析,从而得到天线的频率范围。

表1 等效刚度区间
4 不确定性分析
在动力学方程式中包含有结构刚度矩阵,这些矩阵元素与局部非线性结构六个方向弹性系数等参数有关,可用向量α=[α1α2…αm]T表示,在确定性结构系统动力学分析中,涉及到的是这些结构参数的确定值或中值αC,而在不确定性结构动力学分析中,还需要考虑结构参数的不确定性对动力学分析稳定性的影响。通常对结构参数的不确定性信息掌握较少而难以确定其概率特性,确定不确定参数的界限则相对容易,用区间符号可以表示为:

(9)
其分量形式为:
(i=1,2,…,m)
(10)

利用区间表示法,与中值αC有微小变化的结构参数可表示为:
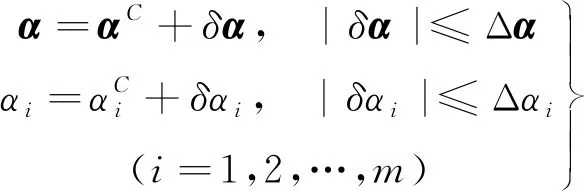
(11)
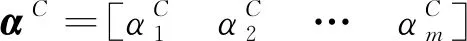
j=1,2,…,n
(12)
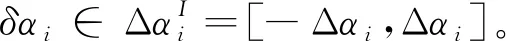
利用区间数学中的区间扩张,由式可得到广义位移响应矢量ω的区间。

(13)
由此可以得到响应的上界:
j=1,2,…,n
(14)
响应的下界:
j=1,2,…,n
(15)
利用区间分析方法,由式(14)和式(15)可以确定出结构的响应区间。
压紧释放机构中两个弹性系数Pz、Mz具有一定的取值范围,可以认为这两个刚度参数在区间内是随机分布的,通过区间分析方法得到天线频率区间。

图13 天线阵型Fig.13 Antenna formation
由图14可知,平动弹性系数Pz、Mz与天线基频具有较强的相关性,在非线性结构等效刚度取值区间得到天线的基频取值范围为[22.0 Hz,24.7 Hz]。
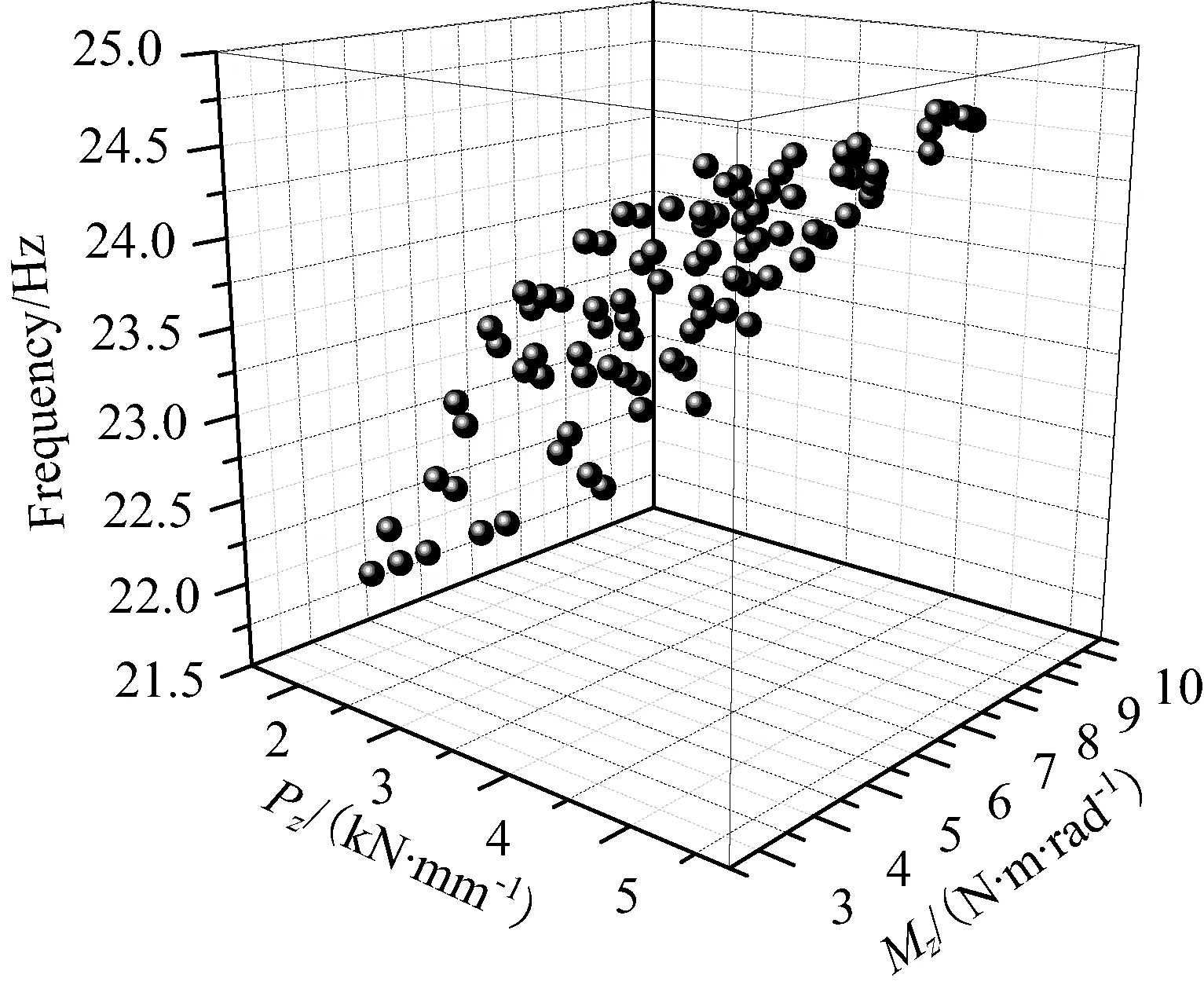
图14 弹性系数Pz、Mz与天线基频分布关系Fig.14 Relation between Pz, Mz and antenna base frequency distribution
5 试验验证
通过分析,天线抱爪构型的压紧释放机构刚度对天线基频影响很大,为了更加真实的在模型中反应其刚度,单独对压紧释放机构进行了静刚度试验,最后对天线进行了模态试验。
(1) 静刚度试验
试验对象为卫星压紧释放机构。通过静力加载测试压紧释放机构刚度,从而得到压紧释放机构六个方向弹性系数(见表3)。
(2)模态试验
在进行锁紧状态模态试验时,天线的约束方式为通过试验工装与刚性平台固支连接,在天线上布置测试振型所必须的试验测点,分别选取天线边缘及天线根部作为激振器激励位置,多次测试天线各阶模态信息,如图15和表2所示。

图15 模态试验结果Fig.15 Modal test results
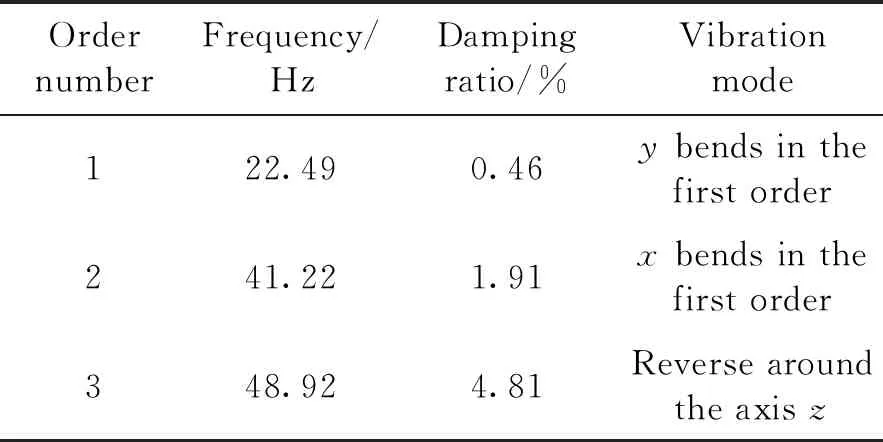
表2 锁紧状态模态频率及模态振型说明
6 试验与分析结果对比
将试验结果与分析结果进行对比。
由表3和表4可知,不考虑压紧释放机构非线性特征所得到的弹性系数值比考虑其非线性特征得到的弹性系数值大很多,试验测试得到的压紧释放机构弹性系数基本包含在非线性分析所得弹性系数区间内,同时天线模态分析考虑非线性和不考虑非线性也存在很大差异,而且通过试验测试验证,分析结果与试验值误差较小,考虑非线性特征与工程实践更为吻合。
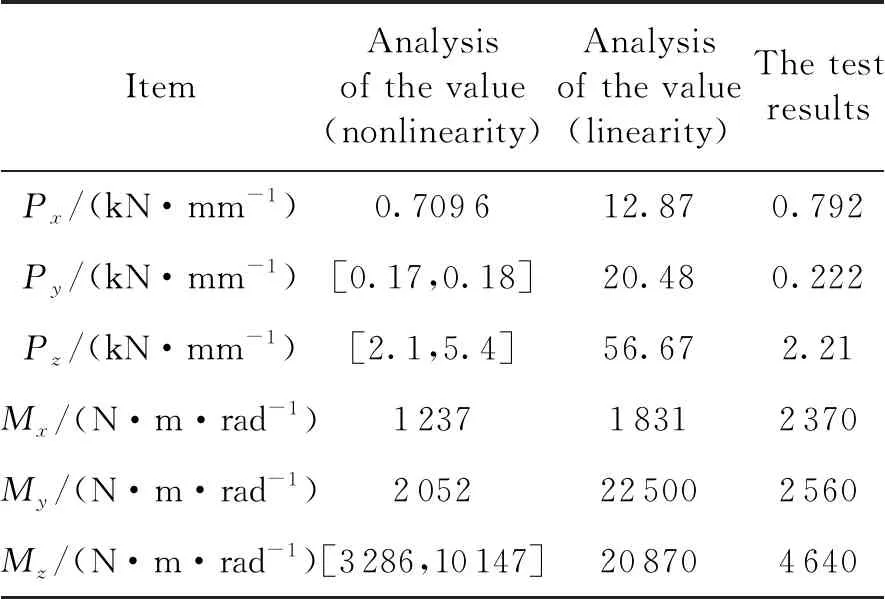
表3 压紧释放机构弹性系数对比
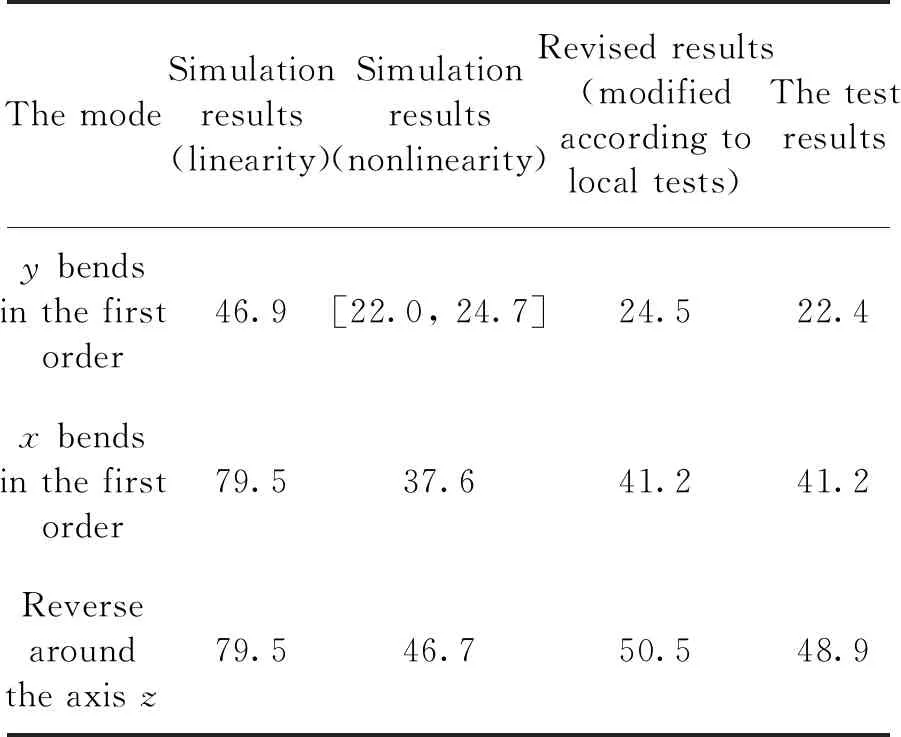
表4 天线模态结果对比
7 结论
本文建立了局部非线性结构模型,详细研究了局部结构的非线性特性,通过理论方式加载得到局部非线性结构的力-位移曲线,根据实际结构的载荷工作区间对结构刚度进行取值,得到局部结构等效刚度区间,最后进行了区间不确定分析,得到了天线动力学特性结果,并通过刚度试验和模态试验验证,得到以下结论:
1)试验结果与分析结果能够很好的吻合,说明了考虑非线性特征因素分析结果的有效性。
2)本研究建立的局部非线性结构等效刚度区间分析方法为卫星天线新型压紧释放机构动力学分析提供了解决途径,分析结果与实际更为吻合、且合理,也为其他局部非线性结构动力学分析提供了参考。
在卫星天线新型压紧释放机构的动力学分析的基础上,可以将等效刚度区间法推广到更多类似的局部非线性结构上去,同时可以对该方法的步骤进行简化和优化,使用更加方便快捷,适合于工程应用推广。
