模块化可展开天线支撑机构运动学建模与分析
2021-10-26范小东郑夕健田大可高旭刘兆晶张珂马小鸥
范小东,郑夕健,田大可,*,高旭,刘兆晶,张珂,马小鸥
1. 沈阳建筑大学 机械工程学院,沈阳 110168 2. 哈尔滨乾行达科技有限公司,哈尔滨 150078 3. 辽宁省科学技术馆,沈阳 110167
1 引言
空间可展开天线是卫星信号传输系统的关键有效载荷之一,是移动通信、卫星导航、对地观测和深空探测等领域不可或缺的航天装备,也是目前国际宇航界研究的一个前沿与热点[1]。近年来,随着空间技术的快速发展和人类对高速智慧通信等需求的增长,对可展开天线提出了大口径、高精度、轻质量的发展要求。模块化可展开天线采用模块化思想设计,可通过改变模块的形状、大小、数量及其组合和排布方式,实现天线口径的快速缩放,可满足未来大口径、超大口径天线的发展需求[2]。并且,随着中国空间站建设的持续深入,大型天线在轨组装成为可能,由六棱柱等构型模块组成的模块化可展开天线是满足在轨组装要求的一种较为理想的结构形式[3]。因此,开展模块化可展开天线相关基础理论研究具有较为重要的科学研究价值和较为重大的应用前景。
运动学分析是进行可展开天线机构设计及运动学与动力学特性等研究的前提和基础。在运动学特性分析方面:文献[4]根据模块的拓扑方法建立了四面体构架式可展开天线展开、收拢构型的数值模型;文献[5]采用螺旋理论研究了由剪叉机构单元构成的平面、圆柱和球面等可展开结构的运动特性;文献[6]采用螺旋理论对Hoberman连杆机构的运动特性进行了分析;文献[7]基于螺旋理论对一种四面体构架式可展开天线进行了自由度计算及运动学分析;文献[8]将Moore-Penrose广义逆理论与空间连杆机构的运动传递矩阵相结合,对一种环状可展机构进行了运动学分析;文献[9]采用坐标变换的方法对环形桁架可展天线机构进行了运动学分析;文献[10]基于螺旋理论对双层环形天线进行了运动学分析;文献[11]采用螺旋理论对一种四面体构架式可展开机构进行了自由度分析及奇异性分析;文献[12]采用D-H法对一种五面体可展开桁架单元进行了运动学分析,并推导了展开过程的运动学方程;文献[13]对由7个六棱柱模块组成的构架式可展开天线的运动学特性进行了研究,建立了运动学模型;文献[14-16]等对日本工程试验卫星(ETS-VIII)天线多模块精确连接的思路及减重方法等进行了简单的介绍,但并未提及如何进行运动学分析。
基于以上阐述,目前对环形桁架式可展开天线机构、四面体构架式可展开天线机构等单模块机构的运动特性研究较多,而对于具有较强空间曲面特征和较强独立连接特征的六棱柱模块化可展开天线机构的运动学方面的研究较少。虽有少数学者对六棱柱构型的运动特性进行了研究,但模块数量较少,对模块的拓展规律及展开过程中的机构特性的研究也有待深入。本文首先根据可展开天线的结构组成及展开原理,建立了机构展开状态下关键点的空间几何模型,随后基于机器人学基础理论,建立了3层共19个模块的可展开天线支撑机构运动学模型,最后采用MATLAB数值仿真软件,对运动学模型进行了验证,并对机构的运动特性进行了分析。
2 结构组成及展开原理
六棱柱模块化可展开天线采用模块化思想设计,由多个结构相似的六棱柱可展开模块组成。每个六棱柱模块由前索网、金属反射网、竖向拉索、后索网和支撑机构等组成,如图1所示。金属反射网是天线的工作表面,主要用于发射和接收信号,完全展开后呈抛物面形状;前索网、竖向拉索、后索网三者共同作用,主要用于金属反射网与支撑机构的连接以及形面精度调节等;支撑机构是一个具有折叠与展开功能的可动机构,是模块的骨架,对金属反射网等柔性结构起到展开及定位的作用。
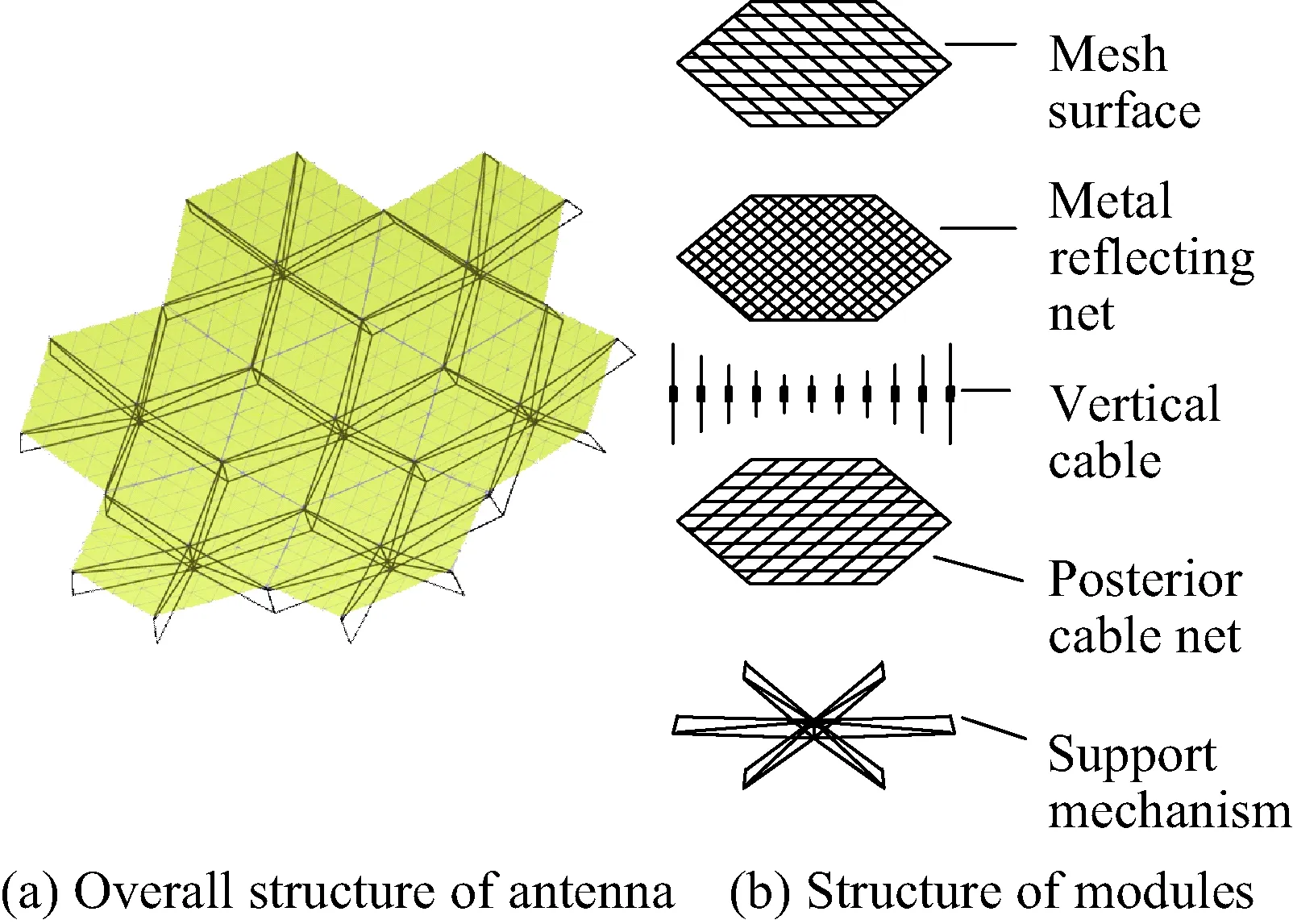
图1 模块化可展开天线结构组成Fig.1 Structure of modular deployable antenna
每个模块的支撑机构由6个周向分布的可展开肋单元组成,每个肋单元主要由滑块、驱动弹簧以及一系列杆件组成,如图2所示。滑块是主动件,收拢状态时,滑块位于肋单元的下部,将驱动弹簧压缩变形,使其产生弹性势能;肋单元展开时,弹簧恢复变形,驱动滑块向上移动,进而带动整个机构展开;完全展开时,机构自锁,由展开过程中的机构转变为稳定的结构。
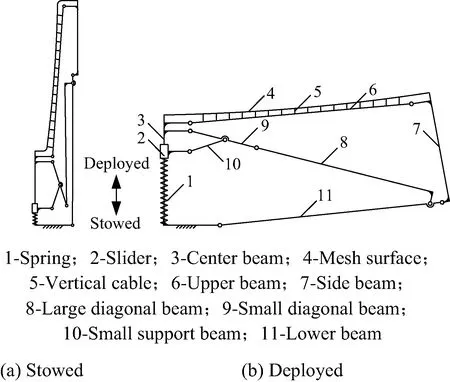
图2 肋单元机构示意Fig.2 Schematic diagram of rib unit mechanism
由于天线的工作表面是抛物面形状,由若干个结构相同或相似的模块组成的可展开天线机构构成球面形状,两者的形状差别通常采用拟合及竖向拉索等方式进行修正和调节[17-18]。由肋单元逐渐演变为可展开天线支撑机构的过程如图3所示。
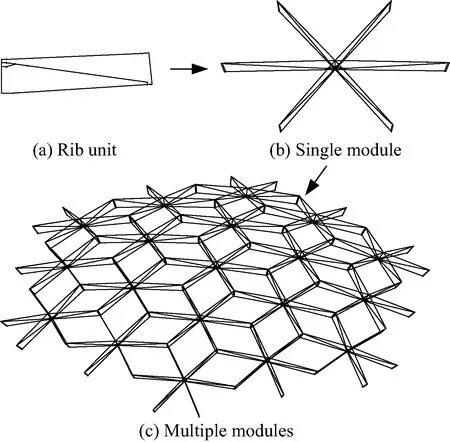
图3 支撑机构组成Fig.3 Composition of support truss
3 可展开天线支撑机构空间几何建模
可展开天线支撑机构的表面为球面构型,如何保证多个六棱柱模块准确连接并精确地“铺设”在该球面上是进行多模块联动运动学建模的前提和基础。由六棱柱模块的结构特点可知,每个模块的6个肋单元其基本尺寸相同,但肋单元之间的夹角不一定相等。多个六棱柱模块可通过调节每个模块内肋单元之间的夹角来实现球面连接,但这些夹角的具体数值以及模块连接点的空间几何坐标未知,空间几何建模能够较好地解决这两个问题。
多个模块在进行球面连接时,其肋单元间夹角的变化并不影响肋单元上关键点的空间总体分布,即关键点总在以半径为r的圆上。本文将单个六棱柱模块简化为一个半径为r的包络圆,用多个半径相等的包络圆构造一个半径为R的球面,通过求解包络圆与包络圆的交点而得到模块与模块连接点的坐标,进而可知支撑机构各个模块的位置与姿态,空间几何建模的流程如图4所示。
用若干个半径为r的包络圆构造一个半径为R的球面,首先需要建立空间直角坐标系,以球心O点为坐标原点,按右手法则建立坐标系{O},如图5。
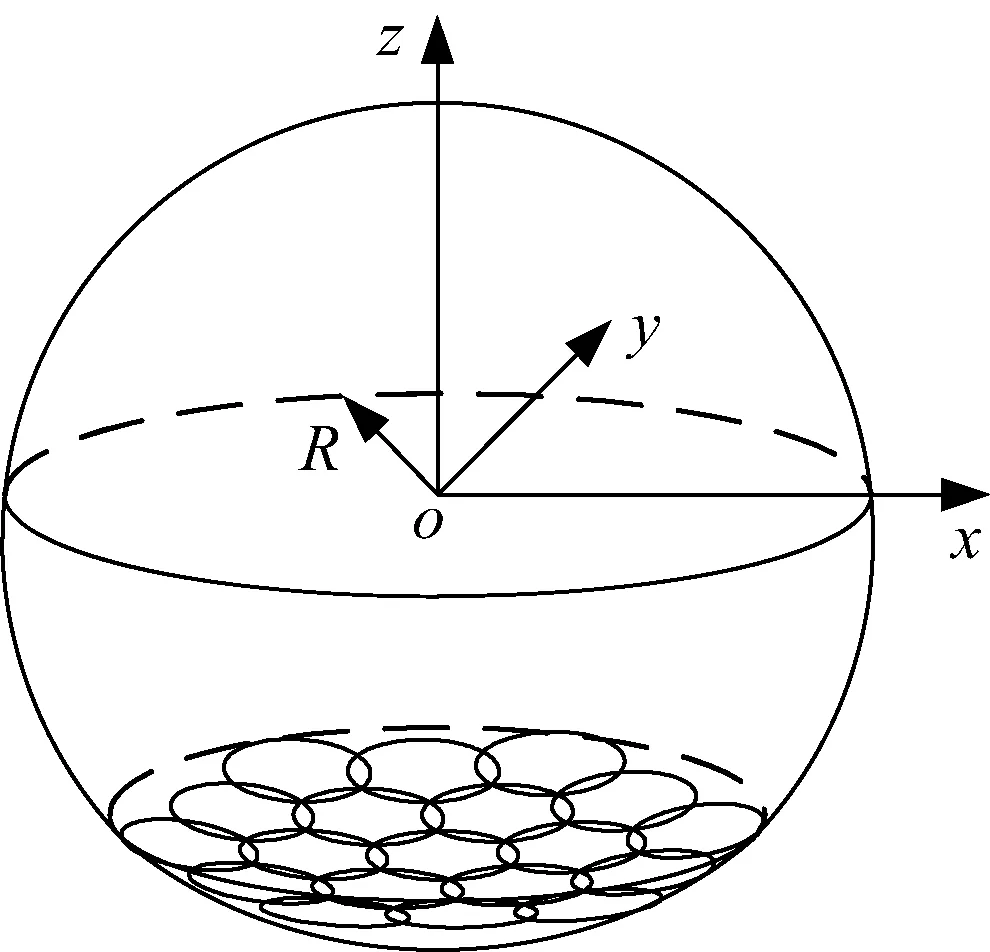
图5 空间直角坐标系Fig.5 Space rectangular coordinate system
图6为图5的俯视图。图6中各包络圆可看成是以包络圆1为中心、以包络圆2~7为第二层、以包络圆8~19为第三层的分层拓扑结构。每层包络圆排列的规律性较强,第二层包络圆3~7可以看作包络圆2绕z轴依次旋转60°得到,第三层包络圆10~19可以看作包络圆8、9绕z轴依次旋转60°得到。因此,只须求出典型包络圆1、2、8、9在坐标系{O}中的方程,就可以知道其他15个包络圆的方程。
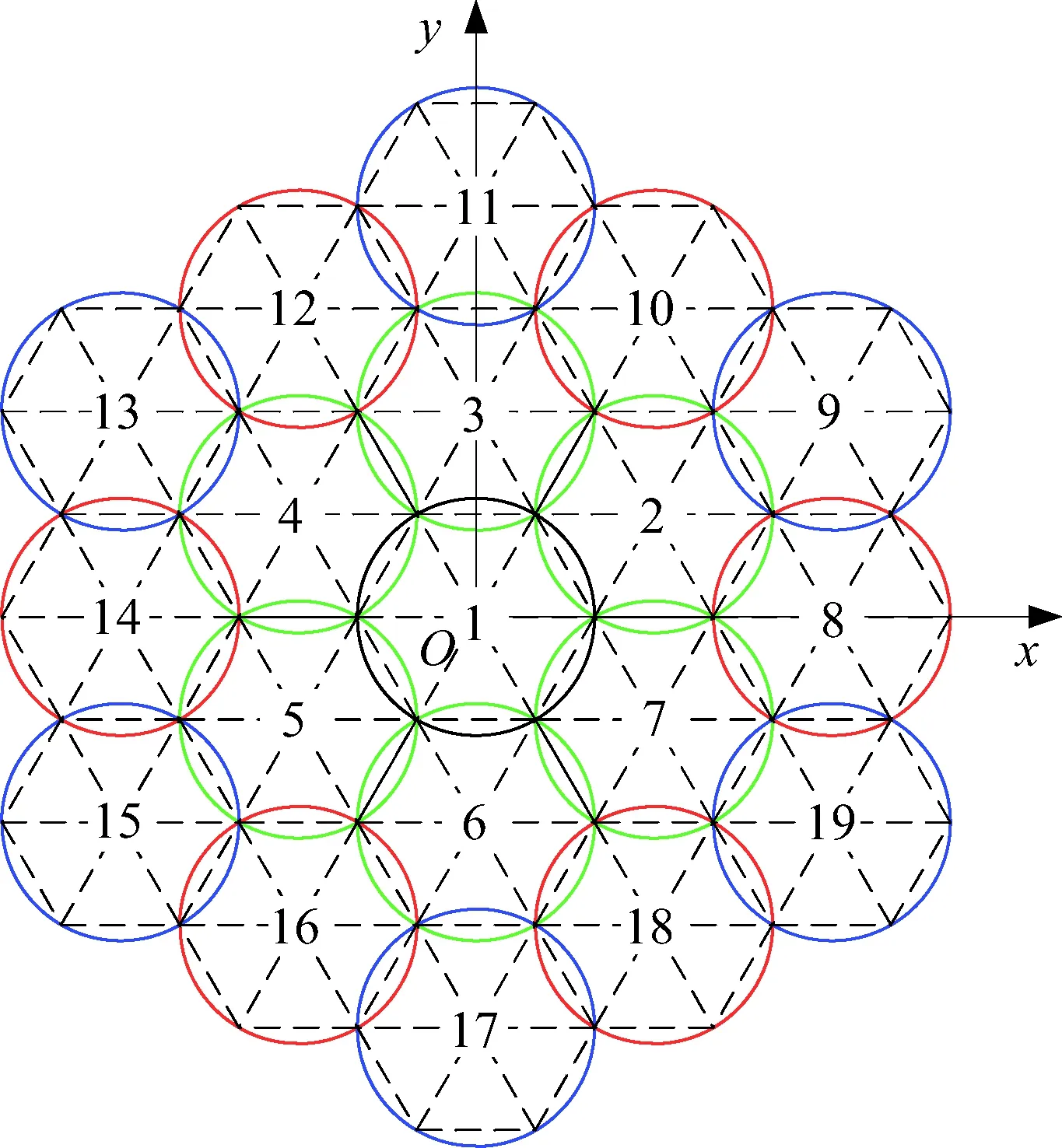
图6 包络圆俯视图Fig.6 Top view of envelope circle


图7 典型包络圆排列规律Fig.7 Arrangement rules of typical envelope circles
为了计算方便,将包络圆n的圆心用Sn表示,n=1,2,…,19。包络圆1在xoz平面的投影,如图8所示。

图8 圆1在xoz平面的投影Fig.8 Projection of circle 1 in xozplane
根据图中的几何关系,并将各点的坐标用向量形式表示,那么,包络圆1的圆心S1的坐标可表示为:
A1点的坐标可表示为:


(1)
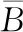
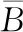

(2)
点B1、B2是包络圆2和8的交点,所以将包络圆2、8的方程联立,可解出B1、B2点的坐标:

(3)
式(3)有两个解,分别是B1、B2点的坐标。

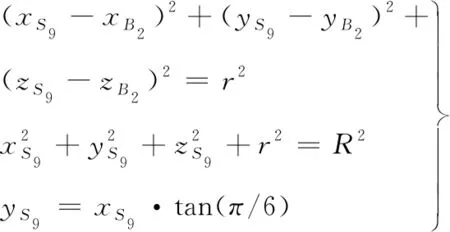
(4)
其余15个包络圆的圆心坐标,可由圆心点S2、S8、S9经坐标变换得到:

(5)
式中:n为包络圆编号,取值范围为1~19;Rot(z,θ)为绕z轴旋转的坐标变换矩阵:

所以,支撑机构的空间几何模型可表示为:
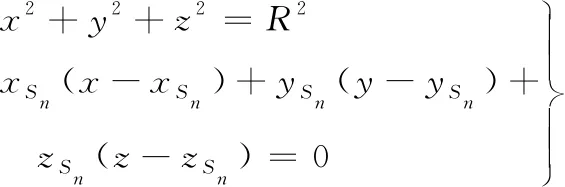
(6)
式中:Sn的取值由式(5)计算得到。
通过几何模型可以计算出模块与模块连接点的坐标,进而通过余弦定理计算出肋单元之间的夹角。现以图7中模块2为例,来说明肋单元之间夹角的计算方法。在ΔS2B2B3中,
(7)
式中:S2表示包络圆2的圆心;LS2B3表示点S2与点B3之间的距离;LS2B2表示点S2与点B2之间的距离。
同理,可以得到模块2内其余5个夹角值,其余模块内肋单元之间的夹角也可以通过该方法计算。
至此,就完成了可展开天线支撑机构的空间几何建模。支撑机构模块与模块之间连接点的坐标、模块内肋单元之间的夹角均可由该模型计算得到。
4 可展开天线支撑机构运动学建模
4.1 D-H法基本原理及建模思路
D-H(Denavit-Hartenberg)法是Denavit和Hartenberg在1955年提出的使用4×4的齐次变换矩阵来描述两个相邻连杆之间空间关系的一种方法[19]。本文中的肋单元是一个平面连杆机构,使用D-H法可以把正向运动学计算问题简化为齐次变换矩阵的运算问题,而矩阵运算可以通过计算机完成,从而大大方便了机构的运动学分析过程。
用D-H法进行运动学建模主要分为四步:建立D-H坐标系、列D-H参数表、求变换矩阵、将各变换矩阵连乘得运动学方程。
(1) 建立D-H坐标系
为了确定各连杆之间的相对运动关系,在每个连杆上分别建立一个坐标系。与机座固接的坐标系记为{0},与连杆i固接的坐标系记为{i},坐标系建立的具体细节参考文献[20]。
(2) 列D-H参数表
D-H法一共有4个参数:
1) 连杆长度ai-1: 连杆两端轴线间的距离;
2) 连杆扭角αi-1:两端轴线间的夹角;
3) 两连杆距离di: 沿关节i轴线上两公垂线的距离;
4) 两连杆夹角θi:垂直于关节i轴线的平面内,两公垂线的夹角。
其中,ai-1和αi-1是描述连杆的参数,di和θi是描述相邻两连杆关系的参数。
每个连杆都有上述4个参数,将所有连杆的参数整理成一张表,即称为D-H参数表。
(3) 求出每个连杆的变换矩阵
每个连杆对应一个坐标系,坐标系{i}相对于坐标系{i-1}的变换矩阵可表示为:
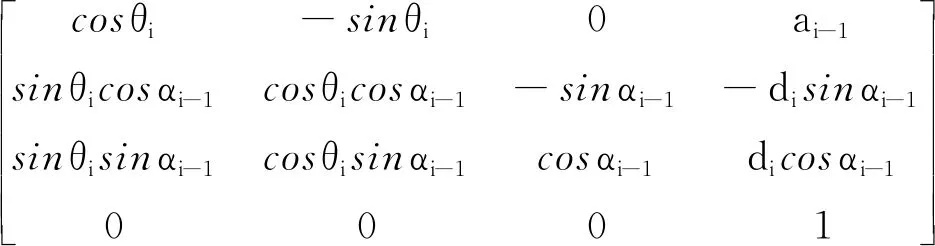
(8)
式中,Rot(x,αi-1)和Rot(z,θi)分别为绕x轴和z轴作旋转变换的旋转齐次坐标变换矩阵;Trans(a,b,c)为沿向量(a,b,c)作平移变换的平移齐次坐标变换矩阵[20]。
(4) 将各变换矩阵连乘,得到运动学方程
将式(8)的变换矩阵连乘,可得到坐标系{i}相对坐标系{0}的变换矩阵(即运动学方程):
式中,nx、ny、nz表示坐标系{i}的x轴相对于坐标系{0}的方向余弦;ox、oy、oz表示坐标系{i}的y轴相对于坐标系{0}的方向余弦;ax、ay、az表示坐标系{i}的z轴相对于坐标系{0}的方向余弦;px、py、pz表示坐标系{i}相对于坐标系{0}的位置坐标。
4.2 肋单元运动学建模
可展开天线支撑机构由多个六棱柱模块组成,每个六棱柱模块又由6个肋单元组成。对可展开天线支撑机构进行运动学分析,须先对肋单元进行运动学分析,在此基础上,再对单个模块进行运动学建模以及对多个模块进行多模块联动建模。
肋单元是一个由多个构件组成的平面连杆机构,也是一种多环闭链可展开机构[21],可将其拆分为3个单环闭链机构:BKMNAB、IJBKPQHI、IJCDEFGI,如图9所示。
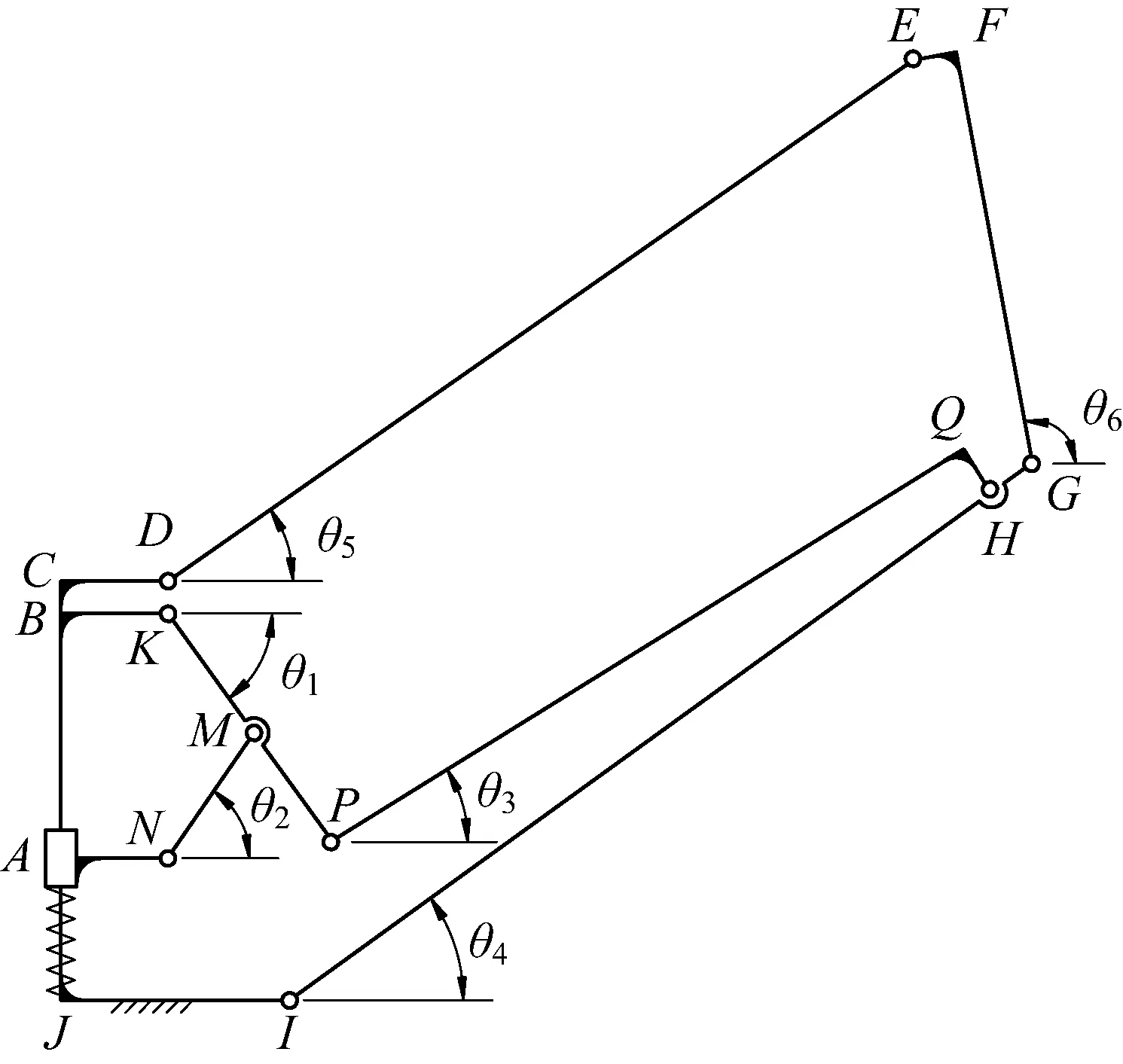
图9 肋单元机构拆分Fig.9 Mechanism of rib unit
D-H坐标系的建立方法如前文所述,在肋单元的每根杆上建立一个坐标系,可建立坐标系{0},{1},…,{14}等15个坐标系,其中坐标系{4}与{0}、{9}与{5}、{14}与{10}重合,坐标系{5}的x轴由I点指向K点、坐标系{10}的x轴由I点指向D点。肋单元的D-H坐标系如图10所示,相应的D-H参数表如表1所示。
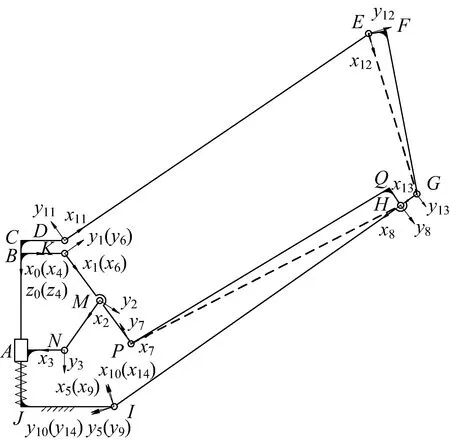
图10 D-H坐标系Fig.10 D-H coordinate system

表1 D-H参数表

(9)
式中:I4表示4阶单位矩阵。
(1)位置分析
解式(9),可得:

(10)
式中:η1的取值为:arctan(LQH/LPQ);η2的取值为: arctan(LEF/LGF),下同。θ1,θ2,…,θ6的值可由式(10)解得。所以,给定滑块A的运动规律,就可以得到机构上任意一点的运动轨迹。
(2)速度分析
将角θ1,θ2,…,θ6的角速度分别记为ω1,ω2,…,ω6。将式(10)对时间求一阶导数可得式(11),由式(11)可以解出角速度ω1,ω2,…,ω6,从而可以知道随着滑块位置的变化,角θ1,θ2,…,θ6的角速度的变化情况,进而可得到各杆件上任一点的速度。
(3)加速度分析
将角θ1,θ2,…,θ6的角加速度分别记为α1,α2,…,α6。将式(10)对时间求二阶导数,可得式(12),由式(12)可解出角加速度α1,α2,…,α6,从而可以知道随着滑块位置的变化,角θ1,θ2,…,θ6的角加速度的变化情况,进而可得到各杆件上任一点的加速度。
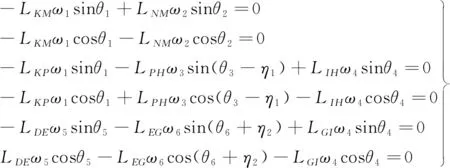
(11)

(12)
在已知滑块位移(LJA或LAB)的情况下,各转动副的角位移、角速度和角加速度可分别通过式(10)~(12)计算得到。至此,就完成了肋单元的运动学建模部分。
4.3 单模块运动学建模
以可展开天线支撑机构所拟合球的球心O为坐标系原点,以肋单元中心杆JC为z轴,方向为由J指向C,以JI杆为x轴,方向为由J指向I,y轴由右手法则确定,可建立图11所示的坐标系。其中,LOF=LOC=R,F点到z轴的距离等于r。

图11 肋单元几何建模Fig.11 Geometric modeling of rib unit
在图11所示的坐标系中,肋单元上各点的坐标可以用一个列向量表示出来,以H点为例(角度标注参考图9):
所以,H点坐标可用列向量表示为:
[xHyHzH]T
同理,肋单元上其余17个点的坐标也可以表示为列向量的形式。
用上述18个点的坐标可以构造肋单元的坐标矩阵U:
矩阵U是肋单元上所有点的坐标的集合。根据上述对肋单元的运动学分析可知,θ1~θ6随滑块A位置的变化而变化,肋单元上点的坐标与θ1~θ6有关,所以矩阵U会随着滑块位置的变化而变化,实时反映肋单元在任意时刻的状态。
在图11中,矩阵U表示肋单元的当前位置,由于一个六棱柱模块可看作是由某个肋单元通过环形阵列而成,所以将矩阵U绕z轴作旋转坐标变换,可以得到组成模块的其余5个肋单元的矩阵Um:
Um=Rot(z,αnm)Um=1,2,…,6
式中:αnm表示模块n(n取值范围为1~19)内肋单元之间的夹角,具体值的求法,参见式(7)。值得注意的一点是,F点到z轴的距离是r,F点坐标会随着滑块位置的变化而变化,即r在肋单元展开或者收拢的过程中是变化的,所以αnm的值在模块展开或者收拢的过程中会随着r的变化而有小幅度的变化。
由于1个模块是由6个肋单元所组成,所以由6个矩阵Um可以组成单个模块的位置矩阵M:
M=[U1U2…U6]
同理,矩阵M是整个模块上所有的点的坐标的集合,它会随着滑块位置的变化而变化,实时反映整个模块在任意时刻的状态。给滑块一个运动函数,矩阵M会根据滑块位置实时反映整个模块上各个点的位置,从而实现对单个模块的运动仿真。
4.4 多模块联动运动学建模
由上述对单模块运动仿真的分析可知,将任何模块的αnm值代入矩阵M,坐标系中矩阵M所表示的模块的位置总是和图6中模块1的位置重合,区别仅仅是不同模块可展开单元之间的夹角值不同。所以,将模块n的一组αnm值代入矩阵M之后,还需要将矩阵M从模块1的位置变换到模块n的位置。将代入αnm值的模块矩阵M记为Mn′,将模块n的矩阵记为Mn,如图6所示,模块1、3、8、11的矩阵可分别表示为:
M1=M1′
式中,Rot(x,θ)和Rot(y,θ)分别为绕x轴和y轴旋转的旋转坐标变换矩阵:


根据模块的排布规律,模块2、4、5、6、7可以看作是由模块3阵列而成,模块10、12、14、16、18可以看作是由模块8阵列而成,模块9、13、15、17、19可以看作是由模块11阵列而成。所以,如果模块3、8、11的矩阵为已知,那么,其余模块的矩阵可经旋转坐标变换得到:

(13)
式(13)给出了19个模块位置矩阵的计算方法。
模块位置矩阵是模块内各个点的坐标的集合,矩阵值会随着滑块A位置的改变而改变,即可以实现随着滑块位置的变化而实时模拟单模块的展开与收拢过程。给滑块设定一个运动函数,r值会随着滑块位置的变换而变化,r值的变化会引起αnm值的变化。αnm值是保证多模块准确连接的关键参数,αnm值随滑块位置实时变化可以保证多个模块在展开与收拢的全过程中实现准确连接。
5 模型验证及分析
为了验证建立的可展开天线支撑机构运动学模型的正确性,采用数值仿真软件MATLAB对几何模型、肋单元运动学模型和多模块联动模型进行验证,并对仿真的结果进行分析。
5.1 几何模型
前期对拟合球及包络圆的参数进行了研究[22],具体参数为:R=4 701 mm、r=600 mm,根据式(6)建立的3层共19个包络圆的几何模型,在软件中的运行结果如图12所示。
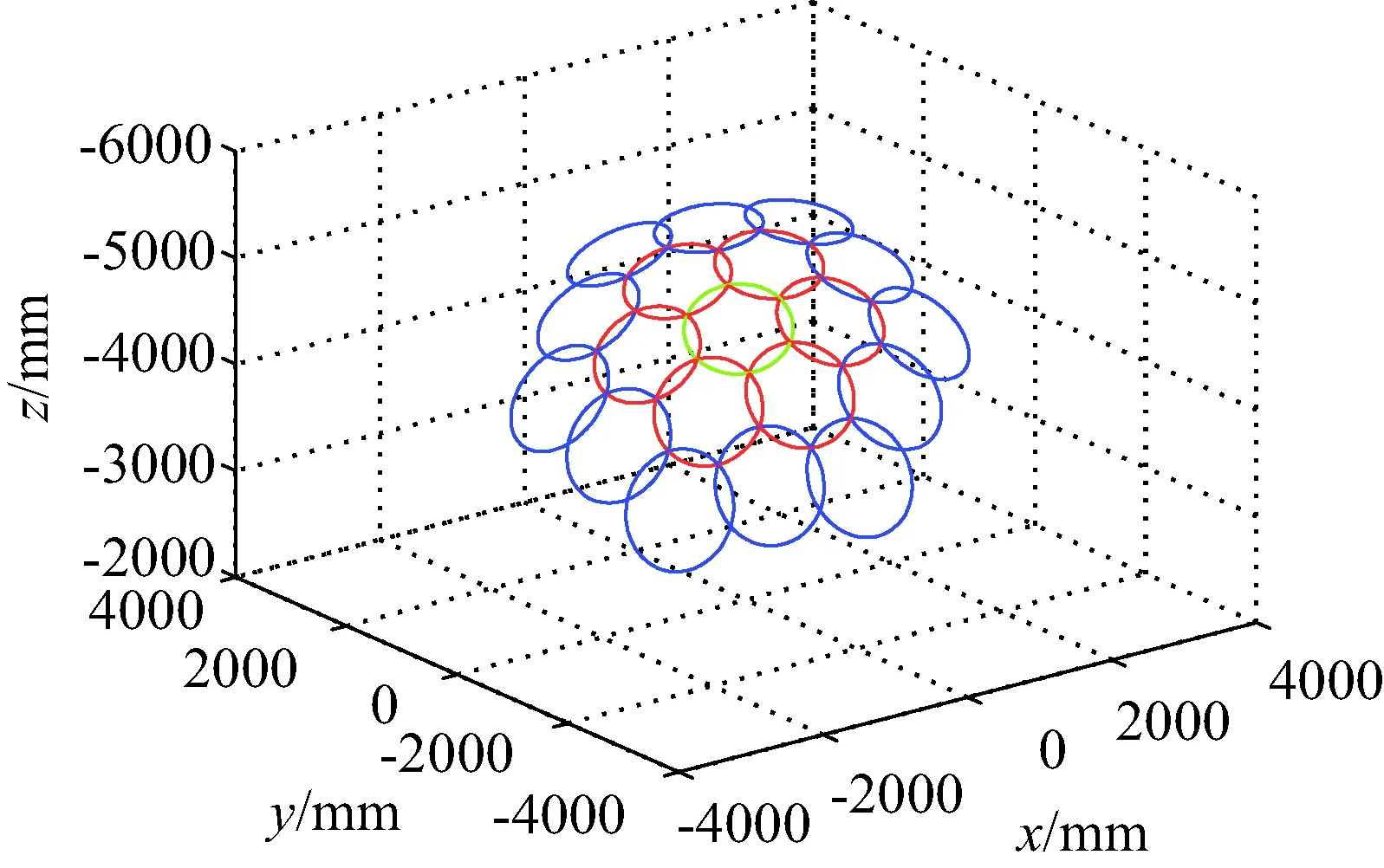
图12 包络圆几何模型Fig.12 Geometric model of enveloping circle
由图12可以看出:(1) 任意相邻三个圆有且仅有一个交点;(2) 19个圆均在同一个球面上;(3) 前两层包络圆,每个圆上都有6个交点,第三层包络圆,一部分圆有5个交点、另一部分圆只有4个交点。由任意相邻三个圆有且仅有一个交点可知,19个圆可由某几个典型圆经阵列得到;由19个圆均在同一个球面上并且每个圆都有6个交点可知,用六边形拟合球面是可行的;由第三层包络圆上的交点数小于6可知,当可展开天线支撑机构只拓扑三层时,由于第三层模块只与第二层及本层模块连接,所以第三层模块内存在不与任何模块相连接的肋单元,这些肋单元与其他肋单元之间的夹角可以在一定范围内给定。
5.2 肋单元运动仿真
根据肋单元的运动学模型,设定滑块的行程为55 mm,设定滑块以1 mm/s的速度匀速运动,那么肋单元从收拢状态运动到展开状态所需的时间为55 s。式(10)(11)(12)分别表示肋单元各个转动副角位移、角速度、角加速度与滑块位移的关系,将其用可视化的方式展现出来,分别如图13~15所示。

图13 角位移曲线Fig.13 Angular displacement curve
图13为肋单元内各个转动副角位移与滑块位移的关系。通过对图13中的数据进行分析,可以发现,肋单元在完全收拢状态时,θ1=83.55°、θ2=83.94°、θ3=88.75°、θ4=89.89°、θ5=88.85°、θ6=90°;肋单元在完全展开状态时,θ1=8.55°、θ2=22.39°、θ3=-8.57°、θ4=3.93°、θ5=2.71°、θ6=97.32°;肋单元在展开过程中,角θ3的变化范围最大,为97.33°,并且在肋单元在完全展开时θ3为负值、θ6大于90°。这些均符合肋单元的运动规律,同时也表明肋单元的运动学模型是正确的。观察图14可以发现,当滑块位移为3 mm时,ω3、ω5达到极值,其他四个角的角速度也从这点之后增速放缓;当滑块位移在区间[3,30]时,机构从非匀速运动阶段逐渐过渡到匀速阶段;当滑块位移在区间[30,55]时,机构趋于匀速运动。这表明当滑块被匀速驱动时,肋单元处于非匀速运动状态。由图15可以看出:当滑块位移在区间[0,10]时,机构运动的加速度较大,当滑块位移在区间[10,55]时,机构运动的加速度逐渐趋于0,运动平稳。
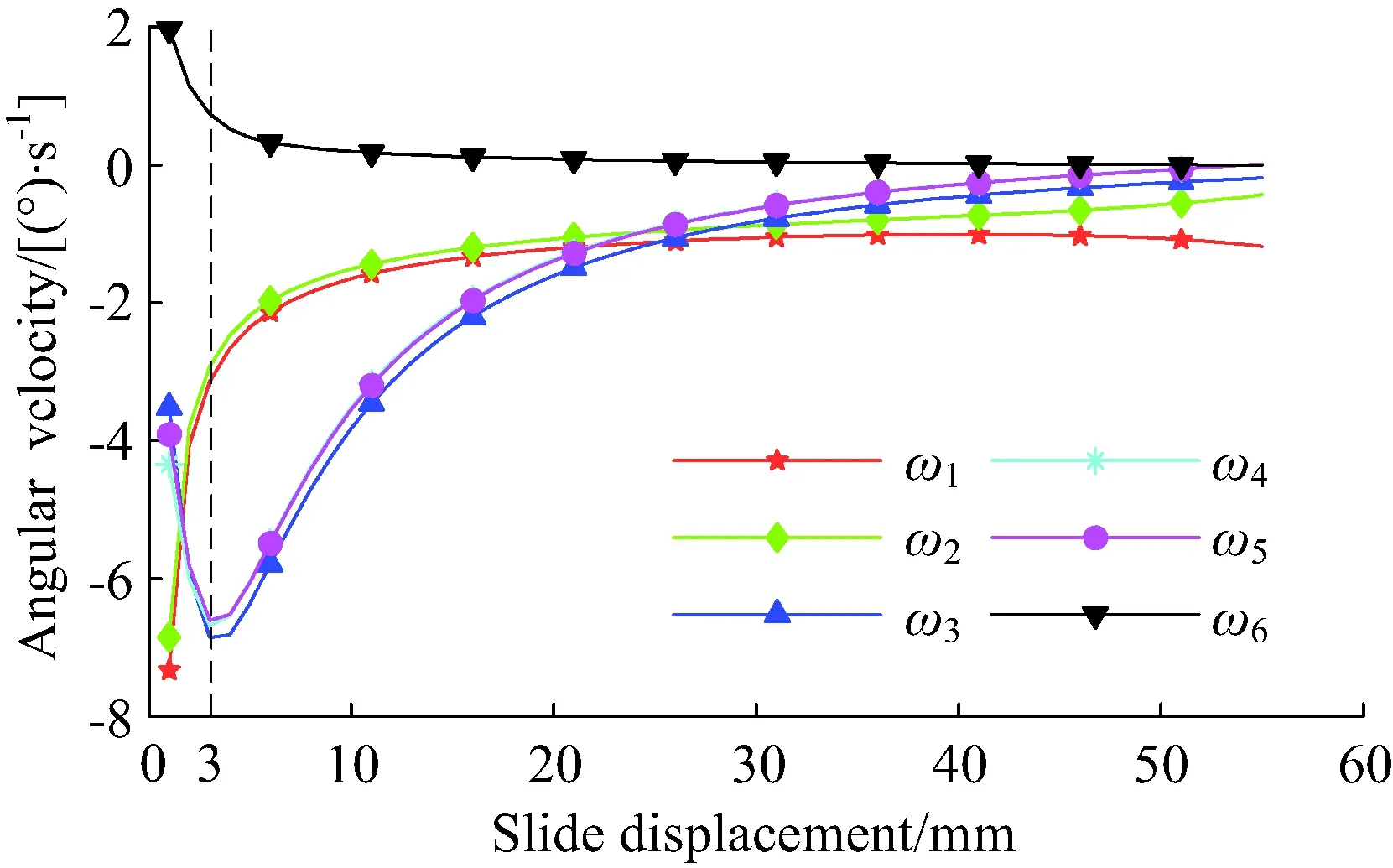
图14 角速度曲线Fig.14 Angular velocity curve

图15 角加速度曲线Fig.15 Angular acceleration curve
5.3 多模块联动仿真
对由19个模块组成的可展开天线支撑机构进行运动学仿真分析。设定滑块的行程为55 mm,并且让滑块以1 mm/s的速度匀速运动。由上述对肋单元运动特性的分析可知,滑块位移在10 mm以内时,肋单元机构的速度和加速度的变化幅度较大,所以取天线支撑机构在t=0 s、t=5 s、t=10 s、t=55 s四个时刻的展开状态,分别如图16~19所示。

图16 完全收拢 (t=0 s)Fig.16 Fully folded (t=0 s)

图17 展开状态一 (t=5 s)Fig.17 Deployment status 1 (t=5 s)

图18 展开状态二 (t=10 s)Fig.18 Deployment status 2 (t=10 s)

图19 完全展开 (t=55 s)Fig.19 Complete deployment (t=55 s)
由图16可以看出,t=0 s时刻,天线支撑机构呈完全收拢状态,与预期结果一致;由图17、18可以看出,此时天线支撑机构正处在展开过程中,19个模块在展开过程中依然能够保持准确连接;由图19可以看出,t=55 s时,天线支撑机构完全展开,各个模块准确连接。所以,由19个模块组成的可展开天线支撑机构能够在保证准确连接的情况下实现同时、同步展开。
为了更好地研究由19个模块组成的可展开天线支撑机构的运动规律,选择其上的关键点进行分析。结合图6与图7可知,模块1~19是由典型模块1、2、8、9经阵列而形成的。根据这一规律,在第三层模块(模块8和9)上取C4、D1、S8和S9等4个点,在第二层模块(模块2)上取B2和S2等2个点,又因为D1点是位置最远的边界点,C4点是模块8和9的连接点,B2点是模块2、8和9的连接点,点S2是模块2的中心点,S8和S9分别是模块8和9的中心点,所以这6个点基本涵盖了天线支撑机构上所有的关键点,这6个点的运动规律基本可以反映整个天线支撑机构的运动规律。
C4、D1、B2、S2、S8和S9等6个点在任意时刻的坐标,可通过多模块联动模型计算出来。取上述6个点到z轴的距离s为因变量,时间t为自变量,通过多模块联动模型可以得到上述6个点的位移随时间t的函数图像,如图20所示。由于根据模型计算出来的数据是一系列离散的点,所以根据离散数学的相关理论,可分别求得对应点的速度和加速度,并可绘制成图21和22所示的图像。

图20 位移曲线Fig.20 Displacement curve

图21 速度曲线Fig.21 Velocity curve
观察图20可以发现,天线支撑机构上不同的关键点具有相似的运动规律,当滑块做匀速运动时,天线支撑机构在0~30 s内完成了大部分的位移,在30~55 s内,各点的位移变化较为缓慢。由图21可以看出,在0~3 s内,天线支撑机构的展开速度一直在增大,在3 s时达到最大,在3~30 s内,展开速度逐渐减小,30 s以后展开速度逐渐趋近于0。由图22可以看出,在0~3 s内,天线支撑机构的展开加速度从最大快速下降到最小,在3~30 s内,展开加速度的绝对值逐渐减小,30 s以后展开加速度逐渐趋近于0。这些均说明天线支撑机构多模块同步展开过程中,当滑块被匀速驱动时,机构上不同的点具有相似的运动规律,多模块同步展开的过程是非匀速的,并且在天线支撑机构的展开过程中,前30 s内完成了大部分的位移,t=3 s时可能会出现运动冲击,但3 s后将平稳展开。
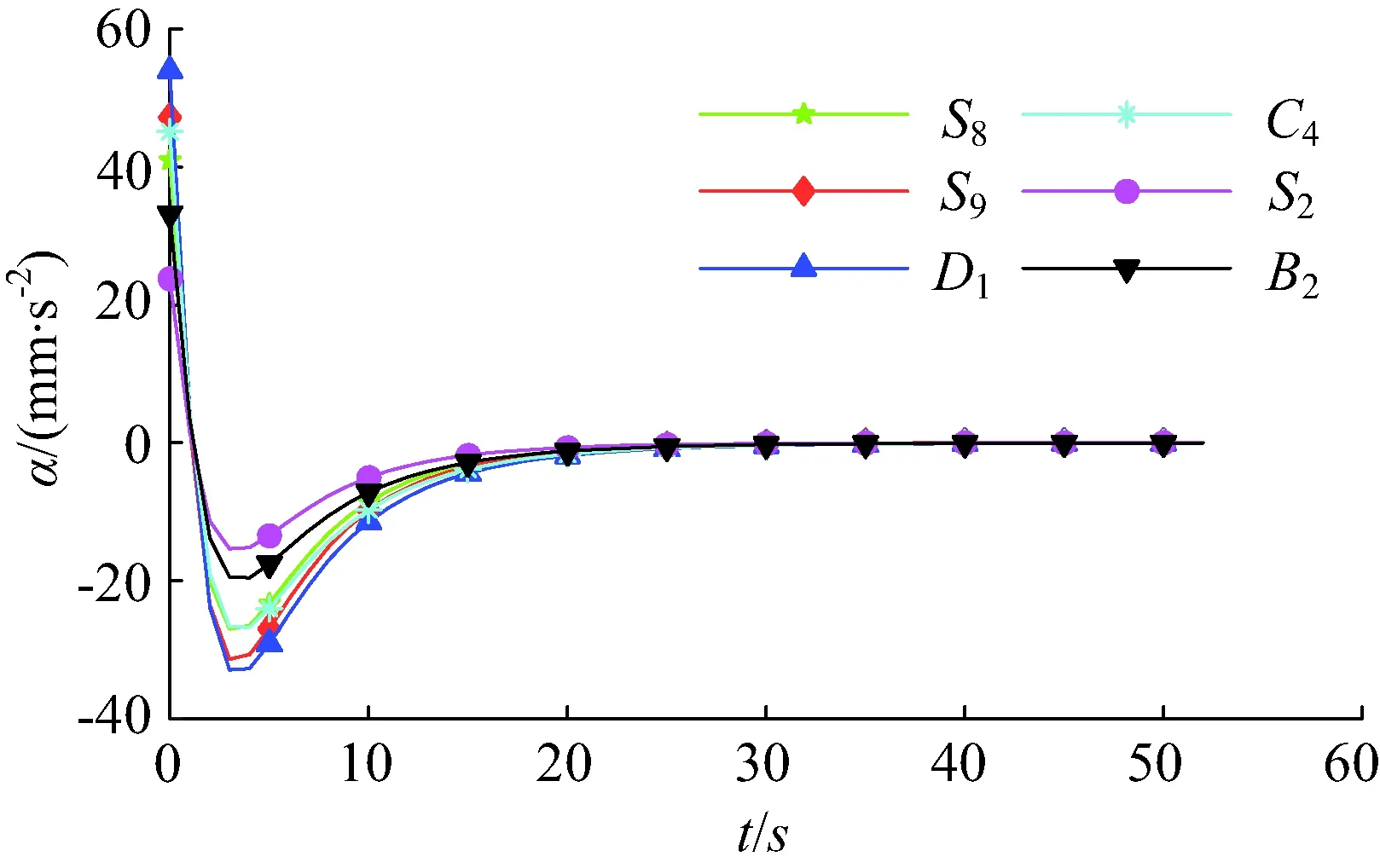
图22 加速度曲线Fig.22 Acceleration curve
6 结论
本文对模块化空间可展开天线支撑机构的运动学问题进行了研究,建立了支撑机构的空间几何模型,同时建立了肋单元、单模块及多模块的运动学模型,并采用数值方法进行了仿真及分析,可得出如下主要结论:
1) 在不改变肋长、仅改变肋与肋夹角的情况下,多个六棱柱模块可以拟合到球面上。
2) 由数值仿真分析可见,所建立的多模块联动运动学模型能较为准确地模拟整个机构的展开过程,表明模型是正确的。
3) 当滑块做匀速运动时,多模块同步展开过程是非匀速的。若要求多模块同步匀速展开或者按预定规律展开,则需要调整滑块的运动规律。
