新型夹纱器压电驱动器的运动特性

马训鸣，李峙毅，吕广雷，陈勇洁

(1.西安工程大学 机电工程学院，陕西 西安 710600；2.西安市现代智能纺织装备重点实验室，陕西 西安 710600)

随着国内外新型无梭织机向高速、高效、智能、节能、模块化应用方向发展[1]，新兴产品的市场需求与生产需求推动织造设备的升级与创新，同时新型织造设备也会促进产品的创新与应用[2]，目前对于织机的研究工作主要集中在辅助喷嘴性能上[3]。夹纱器是织机储纬器控制单元中的重要组成部分之一，通过销子的抬起与落下完成纬纱的定长退绕，控制退绕时间[4]，夹纱器的性能直接影响织机性能及纱线质量。我国大部分纺织机械厂家的技术水平与国际上的先进智能制造技术存在一定的差距，关键部件仍需进口，国产设备竞争力不足，因此，急需研制适用于当代织机高性能要求的新型夹纱器。

压电材料具有正、逆压电效应，可实现电能与机械能之间的相互转化。叠层式压电弯曲片是由若干层压电层叠层构成，片状压电陶瓷作驱动器主要应用于对空间体积、质量以及受力性质有特殊要求的场合[5]。不同材料的压电陶瓷片在非谐振频率下使用时所需电压也不同，主要由其装配方式及预紧力决定。以锆钛酸铅(PZT)为材料的压电陶瓷片作驱动器可执行纳米量级的分辨率和千赫兹量级宽带的阶梯运动，并可提供数瓦级的机械效率[6]，特别适合于微位移驱动。

本文基于压电技术，提出基于压电陶瓷片驱动的新型夹纱器。针对压电夹纱器中所选用的压电陶瓷片驱动器进行系统建模与仿真分析并搭建实验平台进行测试，以期为压电陶瓷片驱动器在夹纱器中的应用提供理论参考。

1 压电夹纱器结构及原理

传统夹纱器采用励磁线圈驱动，其余部件主要由轭铁、定铁芯、弹簧、动铁芯等构成，工作原理可视为吸入式电磁铁[7]。随着工作时长的增加，励磁线圈会由于自身发热而导致端部夹纱针力不足，并且励磁线圈所存在的放电阶段会导致夹纱器抬起与落下的频率响应一致性差，从而导致织机性能下降，严重影响纱线质量。根据市场调研，国产电磁夹纱器落下阶段响应时间一般为8～9.6 ms，进口电磁夹纱器落下阶段响应时间一般为 5～6 ms，均不满足当前织机1 000～1 200 r/min的转速要求。

为解决传统夹纱器存在的缺陷，提高织机的生产效率与技术水平，本文设计了一种压电驱动新型夹纱器，其示意图如图1所示。在满足夹纱器工作需求的前提下，采用压电弯曲片作为驱动器代替励磁线圈驱动，以双柔性铰链新结构作为传动机构，压电片搭载双柔性铰链完成夹纱针的抬落。

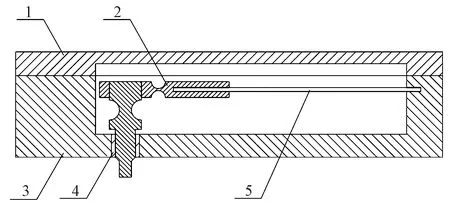
1—上壳体；2—双柔性铰链；3—下壳体；4—滑动轴承；5—压电片。图1 压电夹纱器示意图Fig.1 Schematic diagram of piezoelectric yarn gripper

压电弯曲片在由驱动电源施加电信号产生弯曲运动的同时还会产生沿其轴线方向的微小拉伸位移，如图2所示，该位移在织机高频转速的工作环境下会导致夹纱力不足，长时间工作还会导致针头磨损影响纱线质量。为抵消该位移，采用双柔性铰链结构保证端部夹纱针的运动形式，即2个直圆型柔性铰链互相垂直。

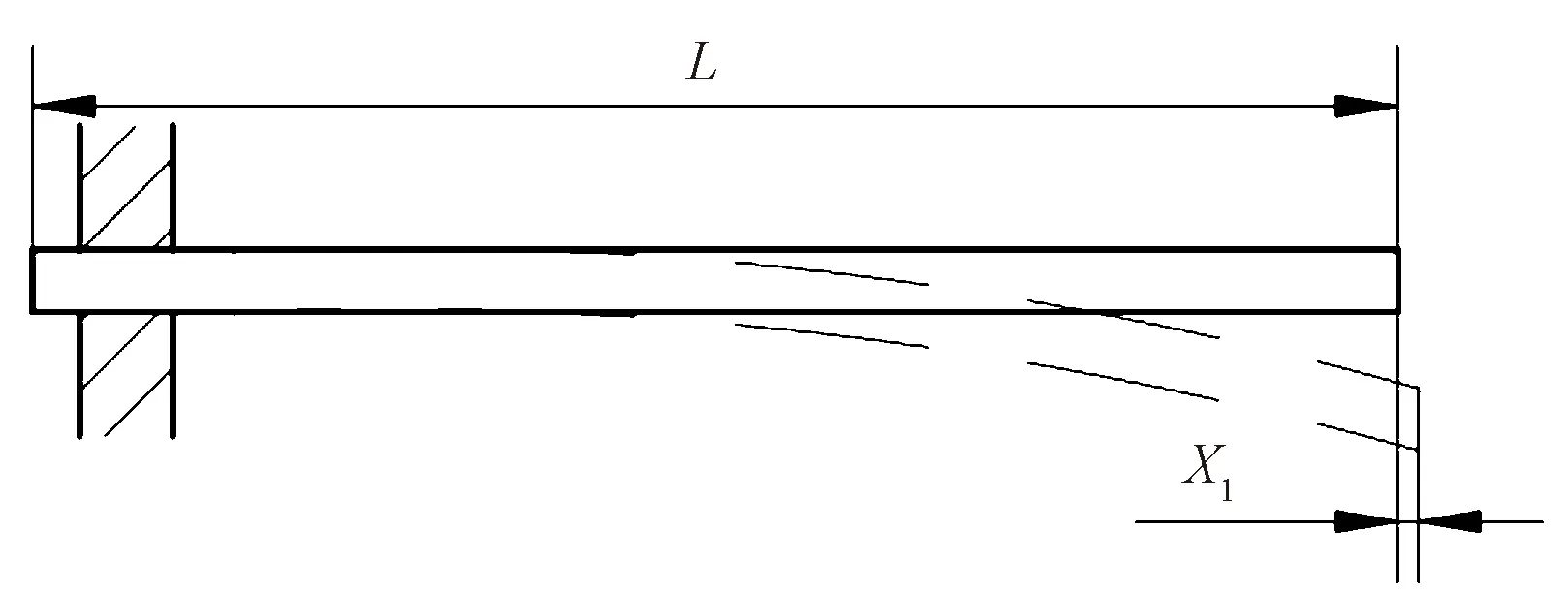
L—压电弯曲片总长；X1—沿轴线方向的微小位移。图2 压电片沿轴线微位移示意图Fig.2 Diagram of piezoelectric plate micro-displacement along axis

在选择压电片型号时，通常需要考虑整体机构的机电转换特性与驱动特性，用数理方法计算压电弯曲片自由端的挠度、转角刚度等自由量，挠度的大小即自由端位移量是衡量压电弯曲片驱动特性的重要参数[8]。通过调研发现，织机夹纱器的工作行程通常为2～3 mm，由此本文采用PZT-3-1.5型叠层式压电弯曲片，总长为68 mm，驱动电压为0～150 V，单向最大输出位移为±1.5 mm，最大输出力为30 N，压电常数为-275×10-12m/V，弹性模量为56×109N/m2，泊松比为0.36。

当外部驱动电源输入-150 V交流电压时，压电弯曲片向一侧弯曲运动，驱动双柔性铰链切口处依次运动，端部夹纱针抬起，此时纱线通过，织机正常工作；当外部电源输入150 V交流电压时，压电双晶片向另一侧运动，夹纱针落下完成夹纱，整个运动行程达3 mm，符合织机夹纱要求。

2 压电弯曲片的静态参数方程

压电夹纱器所选用的PZT-3-1.5型压电弯曲片由10层厚度为0.1 mm的弯曲薄片烧结而成，一端固定呈悬臂状，另一端处于自由状态，故可称为悬臂式压电弯曲片，结构如图3所示。压电弯曲片总长为L，夹持长度为L1，厚度为T；每层压电层的厚度为t。压电夹纱器工作可改变其夹持长度L1，但其总长始终为定值。

图3 悬臂式压电弯曲片示意图Fig.3 Schematic diagram of cantilever piezoelectric bending plate

叠层式压电弯曲片与普通压电双晶片的区别在于没有金属层，因此对于叠层式压电弯曲片静态参数的研究可参考压电双晶片的静态参数研究，只需将含有金属层的参数视为0即可，文献[9]可以佐证这一点。

压电弯曲片沿其轴线方向的微位移只会影响夹纱器的运动精度，不改变整体变形方式，在一端固定的情况下只受弯矩作用。以压电弯曲片的中心线为x轴，垂直于夹持处为y轴，在静态电场的作用下，压电弯曲片的弯矩方程为

(1)

式中：Ep为压电陶瓷的弹性模量，N/mm2；w为压电弯曲片的宽度，mm；E为静态电压值，V；d31为压电常数，mm/V；k1为电场作用下的曲率，mm-1。

若无外部力矩作用，则曲率k1为

(2)

若应用于直流电源驱动情况下，悬臂式压电弯曲片的端部静态挠度值(端部位移)为

(3)

式中，L2为非夹持长度，mm。

悬臂式压电弯曲片端部执行力为

(4)

式中，Ic为压电弯曲片截面惯性矩，mm4。

悬臂式压电弯曲片在安装时夹持力要适中，通常大约为端部输出力的5倍[10]。选用PZT-3-1.5型压电弯曲片，夹持力为150 N。

由式(3)可知，影响位移的参数是非夹持长度L2与每层压电层的厚度t。通过MatLab对式(3)进行仿真，分析端部位移与非夹持长度L2、每层压电层厚度t的关系，结果分别如图4、5所示。压电弯曲片满足位移要求时，非夹持长度为49 nm，结合所选压电弯曲片总长为68 mm，可以得到安装时的夹持长度为19 mm。

图4 非夹持长度与位移关系Fig.4 Relationship between non-clamping length and displacement

图5 每层压电层厚度与位移关系Fig.5 Relationship between thickness and displacement of each layer

通过对比可以看出，非夹持长度对位移的影响较大。一方面可通过式(3)得出不同型号压电弯曲片安装时的夹持长度；另一方面，在压电弯曲片最大位移充足的情况下可通过调整夹持长度得到相应的位移，这种情况下对压电弯曲片在壳体内的固定方式也有一定的要求。

3 压电弯曲片的动态特性

3.1 压电弯曲片动力学模型

压电夹纱器相比传统电磁夹纱器最突出的特点是响应速度快，系统稳定且不受工况的影响，应用范围更广。早在1997年，国外学者Goldfarb等[11-12]便提出了同时包括动态特性与迟滞效应的压电迟滞模型，该模型也是目前最常用的压电陶瓷机电模型，结合该模型将系统等效为弹簧-阻尼-质量块，可建立自由端带有集中质量块的悬臂式压电弯曲片简化动力学模型，如图6所示。图中：m为质量块质量，kg；k为压电弯曲片自由端所受外力与其挠度的比值，N/mm；c为压电弯曲片阻尼。

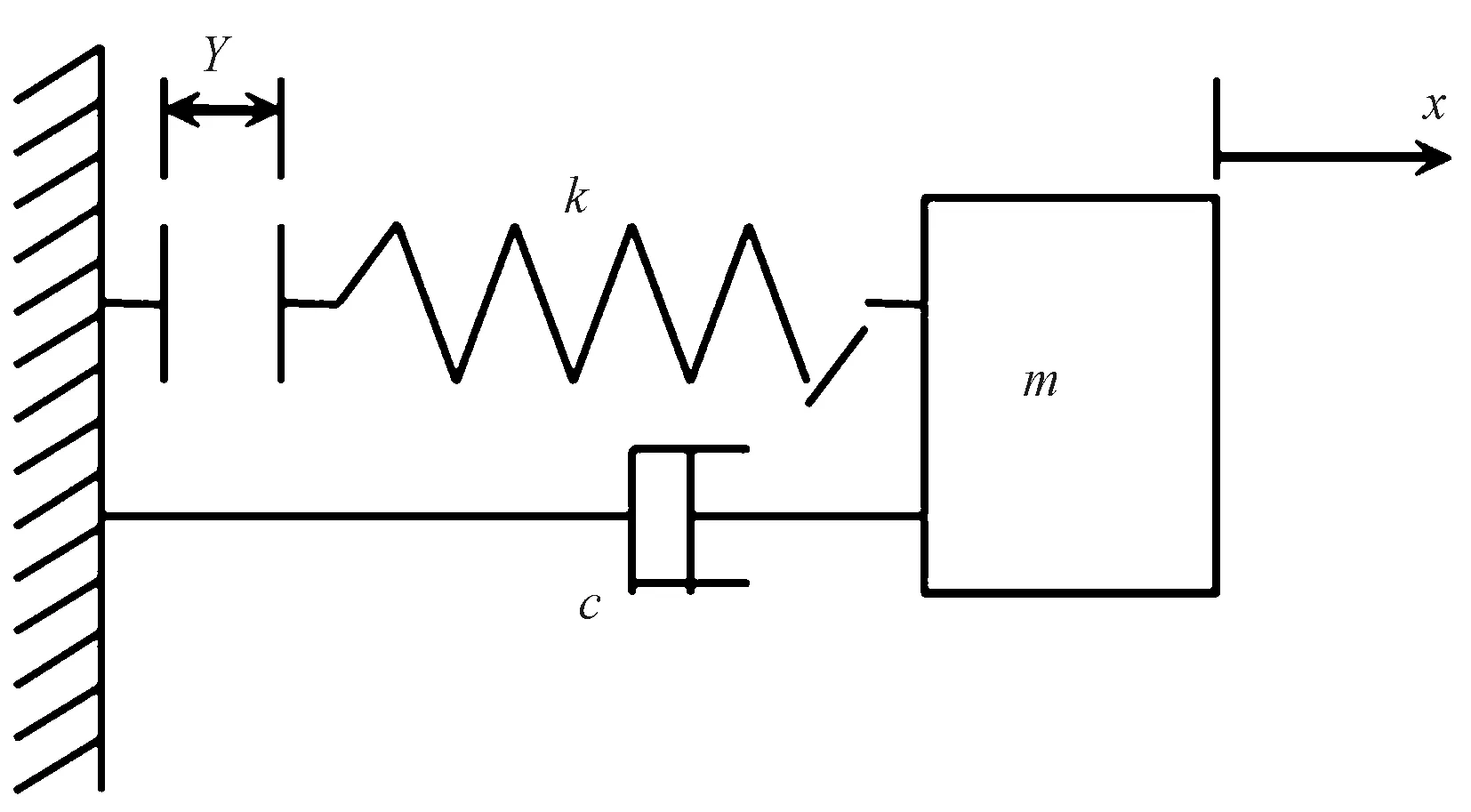
图6 压电弯曲片动力学模型Fig.6 Dynamic model of piezoelectric bending plate

作用于压电弯曲片自由端所受外力与挠度的比值k[13-14]为

(5)

根据动力学模型，可建立压电弯曲片的动力学方程：

(6)

(7)

式中，s为原函数中的微分算子。

3.2 系统分析

根据压电弯曲片的参数与织机工况需求，设定仿真参数m=0.005 3 kg，k=3.0 N/mm，B=0.7。利用MatLab对系统模型进行仿真分析。

图7为阻尼比对系统位移影响的阶跃响应图。当B=0.7时，压电弯曲片稳态输出位移为1.43 mm，与表1中数据拟合度良好，说明该模型符合仿真要求。

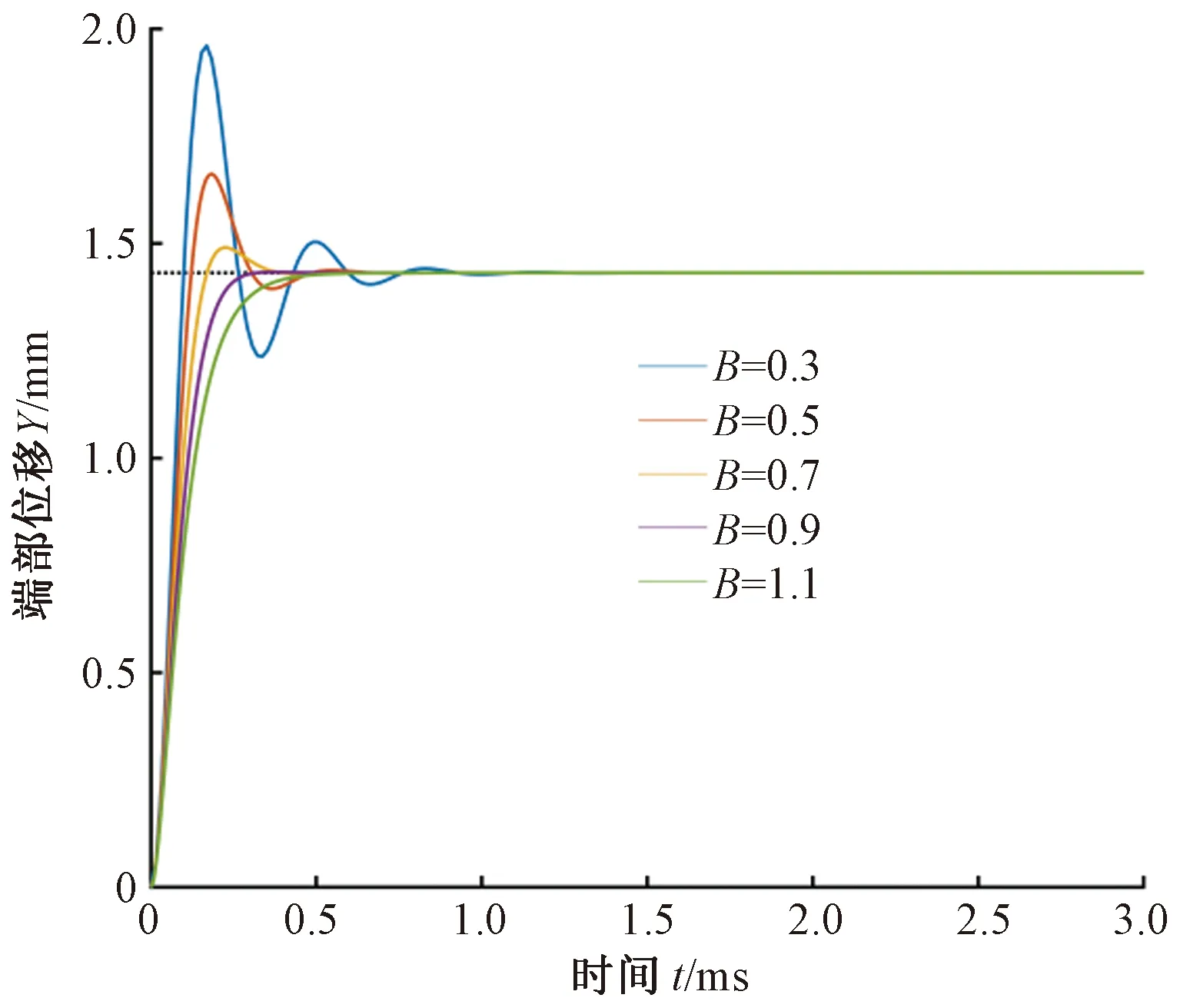
图7 阻尼比对系统的影响Fig.7 Influence of damping ratio on system

阻尼比是影响系统响应稳定性的重要参数，不同的阻尼比使得系统的超调量及调整时间均发生相应的变化[15]。系统的超调量会随着阻尼比B的增大而减小，系统的调整时间也会随阻尼比B的增大而减小。在本文所选压电驱动器上，具体体现在压电夹纱器的抬起与下落。

实际应用中，压电夹纱器需要满足织机的工作频率需求，压电驱动器系统的固有频率是否稳定，将直接影响织机工况的完成情况。从固有频率wn的表达式来看，等效刚度k与等效质量m是影响固有频率wn的2个因素。图8、9分别示出等效刚度与等效质量分别取不同数值时的G(s)阶跃响应特性曲线。

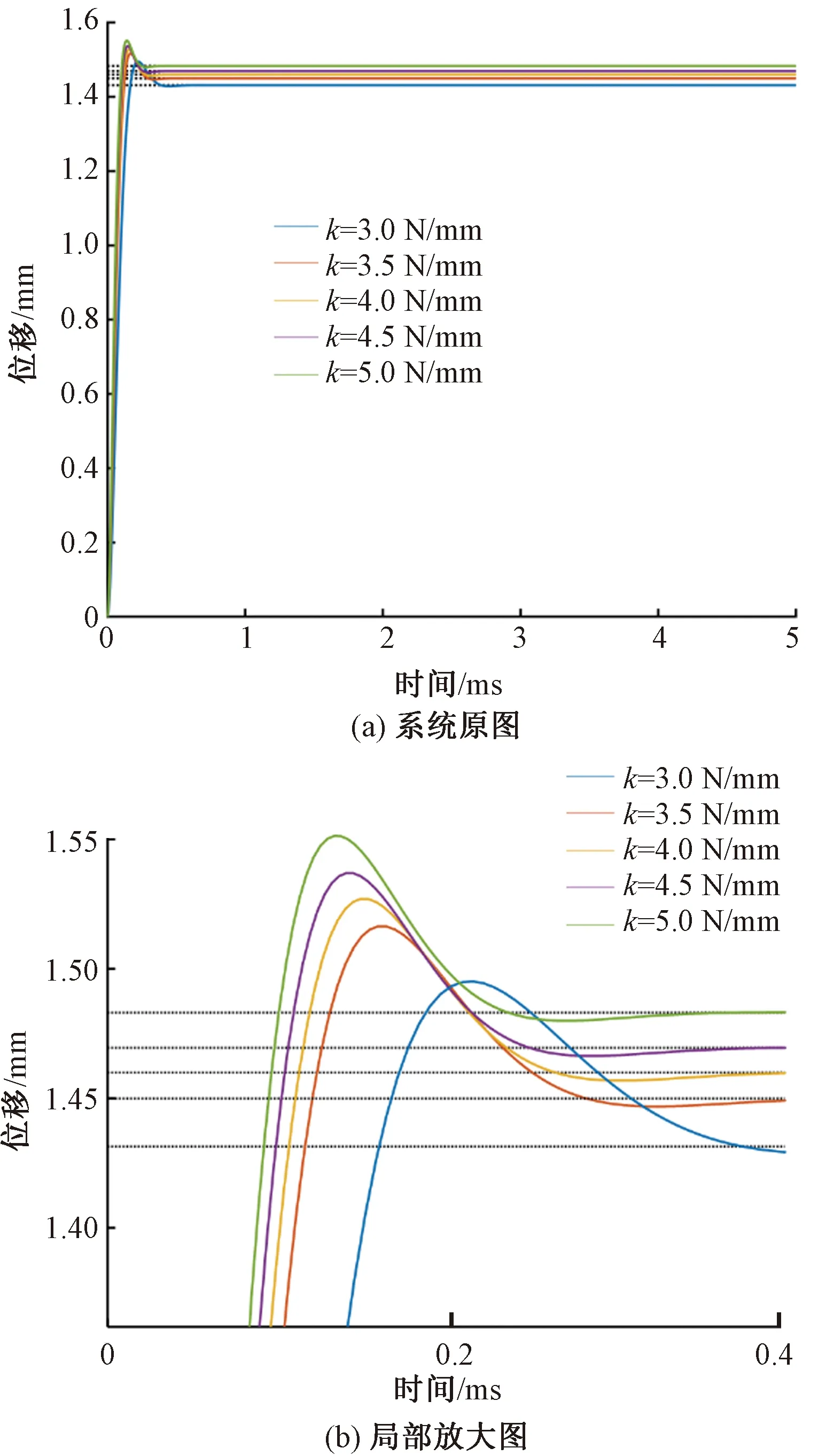
图8 等效刚度对系统的影响Fig.8 Influence of equivalent stiffness on system.(a)Original system；(b)Local enlarged view

由图8可知，wn与k成正比。k的增大伴随着响应时间的加快，稳态输出位移增大，系统到达峰值的时间变快。

从图9可知，等效质量m达到0.006 kg后，系统逐渐出现超调现象；等效质量m越大，超调量越大，稳定时间越长。

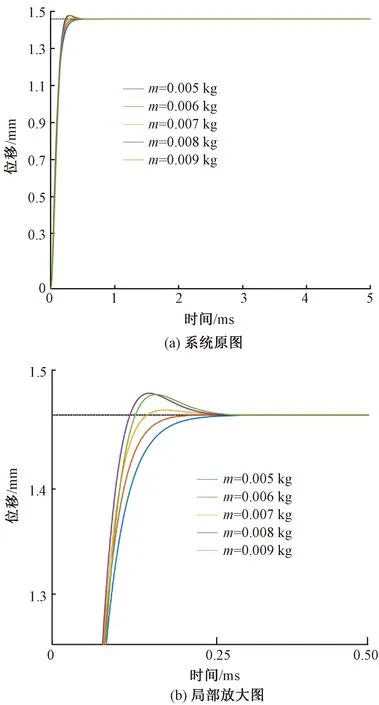
图9 等效质量对系统的影响Fig.9 Influence of equivalent mass on system.(a) Original system.(b) Local enlarged view

为验证系统的稳定性，对系统模型进行求解，得到其零极点图(见图10)。随后通过伯德图表示系统响应频率，进一步验证系统模型的正确性，如图11所示。结果显示，系统模型的根均分布于负半轴，系统稳定性良好。

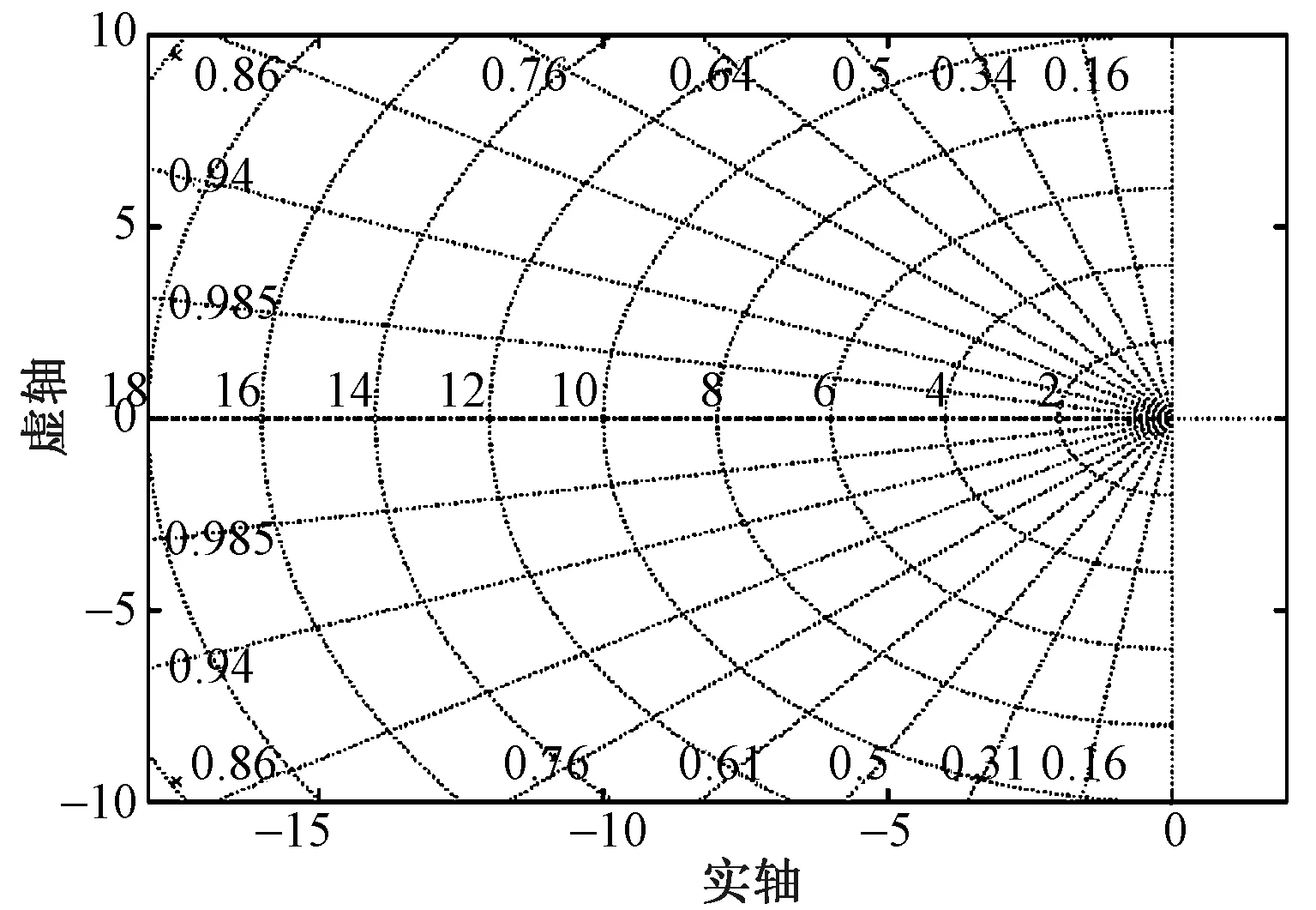
图10 零极点图Fig.10 Pole of zero

图11 系统伯德图Fig.11 Bode diagram.(a)Phase;(b)Amplitude

综合来看，压电驱动器达到最大位移的响应时间可稳定在1.5 ms左右，具有良好的动态特性与输出位移。

4 实验验证

为验证所选压电弯曲片在电压驱动下的运动特性理论分析成果，采用非接触式的测量方法对压电弯曲片的端部位移进行测试。

实验设备主要包括PRO-3300XL传感器(转换比为100 mV/mil)、NI USB-6009采集卡、高频压电陶瓷驱动器以及68×20×1压电片。同时为便于数据采集处理，基于LAVBIEW搭建测试平台。

4.1 悬臂式压电弯曲片端部位移测试平台

叠层式压电弯曲片在电信号激励下产生的变形量相较于其他压电驱动元件偏大，即位移输出量级为毫米级，若采用接触式位移传感器会导致其在接触的瞬间产生反向弹性变形，进而影响测试结果，故采用非接触式电涡流测量方法以提高精度。

传统ZA205、ZA205i型电磁夹纱器通过光敏管的导通时间测量夹纱器的响应速度，测试时励磁线圈的电源激励为10 Hz[16]。为了更好地对比效果，同样给予压电弯曲片10 Hz的电源激励，同时在端部固定与双柔性铰链同等质量的铁片以提高测试效率与准确性。将压电驱动器的电信号施加到压电弯曲片上，利用电涡流位移传感器将端部位移转变为电压数据经采集卡记录至计算机测试平台中。实验测试平台如图12所示。

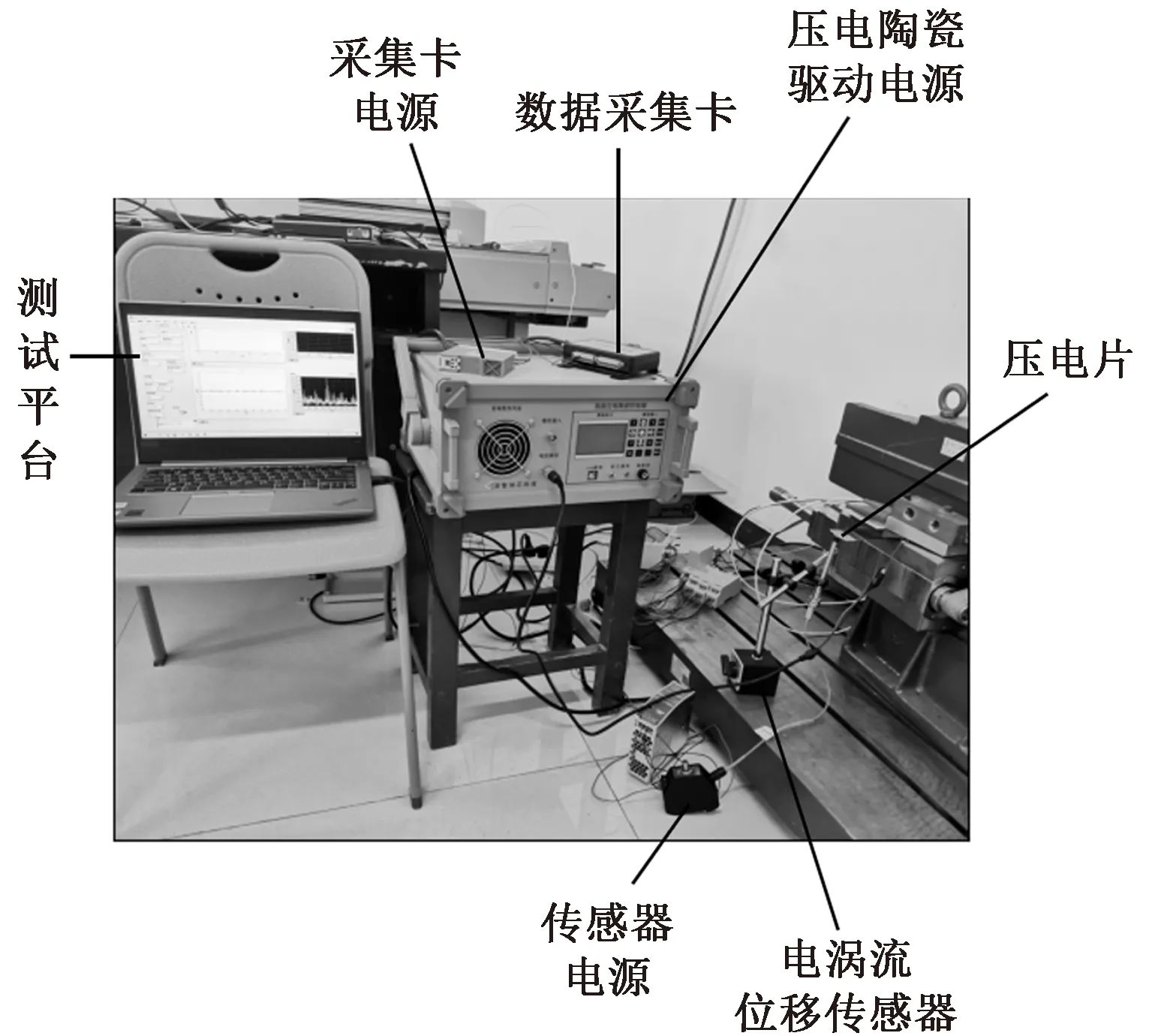
图12 实验测试平台Fig.12 Experimental test platform

4.2 实验测试结果与分析

实验中施加在压电弯曲片上的激励为10 Hz、150 V的电信号，将数据导入MatLab中进行分析可得测试结果，如图13所示。

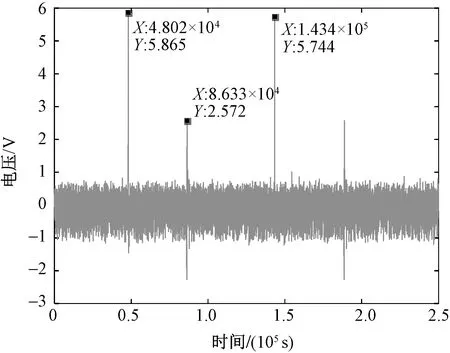
图13 测试结果Fig.13 Test results

从测试结果可知，当压电弯曲片受到电信号激励时产生5.865 V的电压变化。所用电涡流位移传感器的转化比为3 937 mV/mm，经推算可得电压与位移的数量关系为0.254 mm/V，结合测试结果可得端部位移约为1.49 mm。

当压电弯曲片受到复位激励时仍会产生轻微振动，最大约0.65 mm。考虑到夹纱器的实际工作要求，后续可通过加大压电弯曲片层数以稳定其自身振动。

将测试数据进一步分析，程序中加入信号长度(25 500 s)、采样频率(10 000)、时间分辨率、频率分辨率等参数，再将分析结果局部放大，得到如图14所示的数据分析结果。

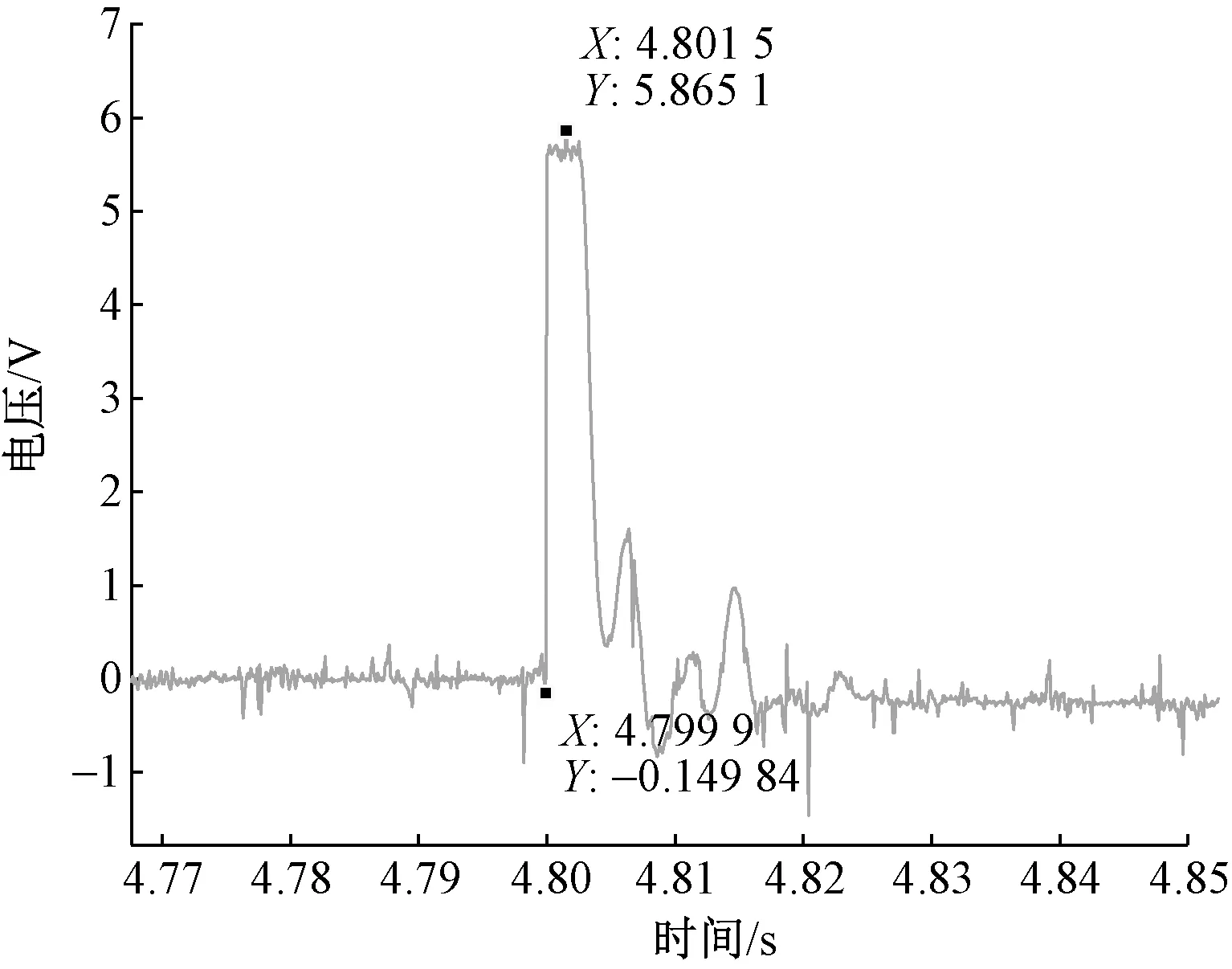
图14 数据分析结果Fig.14 Data analysis results

从进一步的分析结果可知，从压电弯曲片接收到激励至产生最大位移所经过的时间约为1.6 ms。国内生产的电磁夹纱器响应时间普遍为：抬起时间约3 ms，断电落下时间8～9.6 ms。国外生产的进口电磁夹纱器响应时间普遍为：抬起时间约2 ms，断电落下时间5～6 ms。相比之下，压电新型夹纱器响应时间较国内产品2个阶段分别缩短46%、80%；较国外产品分别提高20%、68%，且更经济、适用范围更广。

5 结 论

本文提出一种适用于织机的新型压电夹纱器，分析了压电夹纱器驱动元件压电弯曲片的运动特性并得到以下结论。

1)所选PZT-3-1.5型压电弯曲片最佳夹持长度为19 mm，夹持力约为150 N，可据此推算不同型号压电弯曲片合适的夹持长度与夹持力。

2)当等效模型的阻尼比为0.7，等效质量为0.005 3 kg，刚度为3 N/mm时，压电夹纱器系统达到稳定的时间约为1.5 ms，且具有良好的位移属性与响应特征。

3)通过搭建实验平台进行测试发现，压电驱动元件端部最大位移约为1.49 mm，达到最大位移的响应时间约为1.6 ms，与仿真结果相差不大。对比国内外电磁夹纱器，抬起阶段响应时间分别缩短46%、20%，落下阶段响应时间分别缩短80%、68%。

FZXB