非光滑带钢在粗糙轧辊平整轧制过程中表面微观形貌的转印行为与演变规律
2021-10-23张勃洋张煜东李嘉琪张清东
张勃洋,张煜东,李嘉琪,李 瑞,张清东
北京科技大学机械工程学院,北京 100083
表面微观形貌是冷轧带钢最重要的表面质量指标之一,对诸如镀锡板印铁美观性、高强钢冲压储油性、汽车板表面喷涂鲜映性等微观表面质量[1−2]有显著影响.带钢表面微观形貌通过轧制转印原理制备,即在轧制/平整过程中,将轧辊表面微观形貌(磨削及毛化制备初始形貌)通过界面轧制塑性变形转印到带钢上而形成.平整作为影响冷轧带钢表面微观形貌的最后一道工序,是决定成品带钢最终微观表面质量的关键,但平整轧制过程带钢表面微观形貌的轧制转印控制存在诸多问题,如成品带钢表面粗糙度参数[3−5]无法有效稳定控制在产品目标要求范围内,以及较大粗糙度的工作辊平整较小粗糙度带钢时,发生出口带钢表面粗糙度减小的“负轧制转印”等问题.究其原因在于平整轧制时,不仅入口带钢表面具有微观形貌,而且工作辊表面亦有微观形貌,使得出口带钢表面微观形貌不仅与工作辊表面微观形貌的复印有关,同时与入口带钢表面微观形貌的遗传有关,而来料带钢形貌的遗传和工作辊形貌的复印又取决于工作辊和带钢的初始形貌并受到平整轧制过程的轧制力和张力等工艺参数以及带钢的弹塑性变形行为等特性影响.因此,揭示平整过程带钢表面微观形貌复杂的遗传和演变规律,对控制成品带钢表面微观形貌和提升带钢微观表面质量重要且必要.
目前国内外学者针对带钢表面微观形貌轧制转印进行了大量研究.针对不同用途成品带钢表面粗糙度控制需求,部分学者基于现场实测,采用逐步回归法或神经网络等数理统计方法建立成品带钢表面粗糙度的预测模型,用以指导工业生产,提高成品质量.但该类方法并未从表面微观形貌的轧制转印生成机理出发,不同生产线或机组以及不同强度带钢获得的粗糙度预测模型差异巨大,不具有普适性[6−8].为进一步分析带钢表面微观形貌轧制转印的影响规律,探索带钢表面微观形貌的轧制转印生成机理,部分学者采用轧制实验和理论计算等方法展开研究.具体如,白振华与王骏飞[9]实验分析了100 μm 到50 nm 不同尺度下带钢表面微观形貌的轧制转印行为;Plouraboué与Boehm[10]、Dick 与Lenard[11]、Jiang 与Tieu[12]、陈金山等[13]、徐冬等[14]、高兴昌[15]和张佳康等[16]通过实验研究了不同轧制工艺参数对带钢表面微观形貌的影响规律.而针对带钢表面微观形貌的理论计算研究,目前大部分研究基于连续体介质力学,使用常见的金属塑性求解方法进行计算,如滑移线法[17]、解析法[18−19]和有限元法[20−26]等,这些方法可实现带钢细观尺度粗糙峰弹塑性变形的仿真计算.但上述研究大多没有考虑入口带钢表面微观形貌,将工作辊表面微观形貌抽象为理想粗糙表面(锯齿形粗糙峰、球形粗糙峰假设等),研究光滑带钢与理想粗糙表面有限个粗糙峰的接触变形.而个别考虑入口带钢表面微观形貌的仿真计算,将工作辊假设为光滑轧辊,带钢表面微观形貌基于理想粗糙表面假设,研究光滑轧辊挤压理想粗糙表面带钢的弹塑性变形行为.这些研究都尚未考虑带钢与轧辊同时为粗糙表面,且理想粗糙表面假设与实际粗糙表面相差过大.
针对此,本文基于大量现场实测,获得了不同粗糙度值的电火花毛化轧辊和磨削轧辊表面二维轮廓,以及酸轧出口即平整入口带钢表面二维轮廓数据,在此基础上建立了工作辊与带钢真实二维轮廓接触的有限元仿真模型,并基于工业现场实验验证了仿真模型的准确性,最后利用该仿真模型分析对比工作辊表面粗糙度大于入口带钢表面粗糙度、工作辊表面粗糙度小于入口带钢表面粗糙度、工作辊表面粗糙度与入口带钢表面粗糙度接近等不同情况下,带钢表面微观形貌的遗传和演变规律.
1 粗糙轧辊轧制非光滑带钢表面微观形貌轧制转印模型的建立与验证
1.1 带钢三维表面微观形貌实测
目前,以宝钢为代表的各大钢铁生产企业大多使用电火花毛化轧辊或磨削加工轧辊轧制转印制备带钢表面微观形貌,通过现场取样并采用RTEC 公司的白光干涉三维形貌仪实测带钢表面微观形貌(XY 舞台分辨率为0.1 μm,高度分辨率为1 nm),如图1 所示,电火花毛化轧辊轧制转印带钢表面形貌存在明显的凸起和凹坑,且不存在明显的各向异性,而磨削轧辊轧制转印带钢表面形貌则存在明显的磨削纹理,且具有明显的各向异性.因此对比两种典型带钢表面微观形貌轧制方向与板宽方向二维轮廓和粗糙度参数,分别见图2 与表1(Ra代表轮廓算术平均偏差,μm;Rz代表微观不平度十点高度,μm;Ry代表轮廓最大高度,μm;Pc代表峰密度,即1 cm 内粗糙度峰值个数,cm−1),对比发现,电火花毛化轧辊轧制转印带钢二维轮廓沿轧制方向与板宽方向近似一致,且粗糙度参数分布范围基本重合,而磨削轧辊轧制转印带钢二维轮廓沿轧制方向与板宽方向明显不同,且粗糙度参数存在较大差异.

表1 两种典型带钢表面微观形貌轧制与板宽方向二维轮廓粗糙度参数Table 1 Roughness parameters of two-dimensional profile along the width and rolling direction of two kinds of typical strip surface microtopography

图1 不同加工方式工作辊轧制带钢表面三维微观形貌.(a)电火花加工;(b)磨削加工Fig.1 Three-dimensional micromorphology of strip surface rolled by work roll with different machining methods:(a) electrical discharge machining;(b) grinding machine

图2 两种典型带钢表面微观形貌轧制与板宽方向二维轮廓.(a)电火花加工;(b)磨削加工Fig.2 Two-dimensional profile along the width and rolling direction of two kinds of typical strip surface microtopography:(a) electrical discharge machining;(b) grinding machine
1.2 模型建立
带钢表面微观形貌的轧制转印机理可归纳为压入、犁沟和挤压作用,带钢表面微观形貌的实测结果表明带钢形貌主要取决于轧辊表面形貌,其轧制方向的相对位移对带钢最终表面形貌影响有限,分析认为虽然在轧制变形区内工作辊与带钢存在轧制方向相对位移,但并未形成有效形貌,这是由于相对运动后带钢仍会与轧辊其他位置接触并产生压下变形,由此只有在离开轧辊的出口区域才有可能形成有效犁沟,对比带钢的压入作用,犁沟作用对生成带钢表面形貌影响不大.因此忽略微凸体犁沟作用,重点考虑工作辊轮廓在带钢表面的压入和挤压作用,建立平整轧制过程粗糙工作辊与非光滑带钢的轧制转印模型.从带钢出口方向正视辊缝,工作辊与带钢的几何模型(局部放大)如图3 所示.

图3 平整轧制过程粗糙工作辊与非光滑带钢轧制转印模型.(a)三维模型;(b)局部放大图Fig.3 Three-dimensional model of rolling transfer of rough work roll and non-smooth strip during flat rolling:(a)three-dimensional model;(b) partial enlarged drawing
本文采用有限元商业软件ANSYS,针对平整轧制过程工作辊与带钢的轧制转印生成建立二维平面仿真模型.模型中工作辊与带钢的几何宽度(x向)均取4000 μm,在工作辊上表面施加均布轧制压力,方向为负z向.工作辊下压过程中,其下表面轮廓与带钢上表面轮廓(粗糙表面)相互作用.模型的侧向边界(x=0 μm 和x=4000 μm)采用增广拉格朗日函数,约束其侧面全部节点的水平位移(x向),并对带钢下表面施加垂向位移(z向)约束.仿真模型采用二维平面应变单元Plane182,并对带钢和工作辊接触区域进行网格加密处理,以提高计算精度.工作辊和带钢均采用理想弹塑性本构模型,其弹性模量均为210 GPa.模型共包含240000 个单元,工作辊与带钢(光滑接触表面)的仿真模型网格图(局部放大)如图4 所示.

图4 工作辊与带钢二维平面仿真模型.(a)平面压入几何模型;(b)有限元仿真网格划分Fig.4 Two-dimensional plane simulation model of work roll and strip:(a) geometric model of two-dimensional profile plane pressing on strip surface;(b) mesh generation of finite element simulation
1.3 实验验证
为验证仿真模型的准确性,依托某平整机组开展工业实验,实测不同生产工况轧后带钢表面二维轮廓形状和粗糙度参数,并采用本文建立的模型计算相应工况条件下轧后带钢表面二维轮廓形状和粗糙度参数,然后对比分析,具体工况如表2所示.

表2 工业实验工况表Table 2 Industrial experiment condition
基于上述生产工况,计算平整后带钢表面微观形貌及其粗糙度参数,并与实测带钢表面粗糙度参数进行对比,包括Ra,Rz,Ry和Pc,具体结果见表3.如表3 所示,计算Ra值的绝对误差小于0.06 μm,相对误差在5.8%以内;Rz与Ry值绝对误差不超过0.26 μm,相对误差在5.9%以内;Pc值绝对误差最大为7 cm−1,相对误差最在10%以内,定量验证了模型的准确性.

表3 模型计算带钢表面粗糙度参数与实验实测值对比Table 3 Comparison between model calculation parameters of strip surface roughness and experimental values
2 带钢表面微观形貌的遗传和演变规律
带钢平整轧制所用工作辊粗糙度较大时,多采用电火花毛化加工,轮廓算术平均偏差Ra一般在1.5~3.5 μm 范围内,而所用工作辊的粗糙度较小时,则多采用磨削工艺加工,轮廓算术平均偏差Ra一般在0.3~1.2 μm 范围内.入口带钢表面粗糙度值则取决于前序冷轧机组末机架轧后带钢表面粗糙度值,本文基于现场大量实测,发现入口带钢轮廓算术平均偏差Ra通常在0.2~1.4 μm 范围内.因此,根据工作辊与入口带钢表面轮廓算术平均偏差Ra的大小关系,分别研究工作辊表面粗糙度大于带钢、工作辊表面粗糙度小于带钢以及工作辊与带钢表面粗糙度接近的三种情况下带钢表面微观形貌的遗传和演变规律.
2.1 工况设计
针对工作辊表面粗糙度大于带钢、工作辊表面粗糙度小于带钢和工作辊与带钢表面粗糙度接近三种情况,设计工况如表4 所示.

表4 带钢表面粗糙度遗传和演变规律计算工况Table 4 Calculation condition of genetic and evolution rule of strip surface roughness
2.2 结果分析与讨论
针对上述三种不同情况,分别计算不同单位板宽轧制力工况下对应的出口带钢轮廓算术平均偏差Ra,对比发现:
(1)如图5 所示,当单位板宽轧制力较小时,出口带钢表面微观形貌主要为入口带钢表面微观形貌的遗传;当单位板宽轧制力适中时,出口带钢表面微观形貌取决于入口带钢表面微观形貌的遗传与工作辊表面微观形貌的复印叠加;当单位板宽轧制力较大时,出口带钢表面微观形貌主要取决于工作辊表面微观形貌的复印.
(2)如图5 所示,当工作辊表面粗糙度小于入口带钢表面粗糙度或两者相近时,出口带钢表面粗糙度都小于入口带钢表面粗糙度;而当工作辊表面粗糙度大于入口带钢表面粗糙度时,在较小的单位板宽轧制力情况下,亦会出现出口带钢表面粗糙度小于入口带钢表面粗糙度的情况.究其原因在于,如图6(a)所示,当单位板宽轧制力较小时,工作辊表面形貌尖峰以挤压带钢表面形貌尖峰为主,带钢表面形貌尖峰降低,带钢表面粗糙度减小.这说明,即使工作辊表面粗糙度大于来料带钢表面粗糙度,在较小的平整轧制力情况下亦会出现“负轧制转印”的现象.

图5 不同轧制力下带钢表面粗糙度遗传和演变规律Fig.5 Inheritance and evolution of strip surface roughness under different rolling forces
(3)如图6(b)所示,当工作辊表面粗糙度大于入口带钢表面粗糙度时,在单位板宽轧制力一定时,工作辊表面形貌尖峰压入带钢表面,并使得带钢表面形貌产生隆起,单位板宽轧制力对带钢表面形貌轧制转印影响较大.而当轧制力进一步增大,工作辊表面形貌尖峰完全进入带钢表面,此时工作辊凹坑被隆起的带钢表面金属逐渐填充,此时单位板宽轧制力对带钢表面形貌轧制转印影响较小.上述分析说明,在带钢表面微观形貌轧制转印过程中,如果带钢表面微观形貌轧制转印处于图6(b)状态,轧制力的波动对出口带钢表面微观形貌影响较大,而如果带钢表面微观形貌轧制转印稳定地控制在图6(c)状态,则轧制力波动对带钢表面微观形貌的影响较小,所以为保证出口带钢表面微观形貌的一致性,确保出口带钢表面粗糙度参数稳定控制在目标范围内,希望带钢表面微观形貌轧制转印过程稳定在图6(c)状态.

图6 不同单位板宽轧制力下带钢与工作辊的位移场分布.(a)带钢尖峰挤压;(b)轧辊尖峰压入;(c)轧辊凹坑填充;(d)轧制转印饱和Fig.6 Displacement field distribution of strip and work roll under different rolling forces:(a) strip peak extrusion;(b) roll peak extrusion;(c) roll pit filling;(d) rolling transfer saturation
(4)如图6(d)所示,当轧制力大到一定程度时,工作辊表面形貌凹坑近乎被填满时,此时带钢表面粗糙度轧制转印保持不变,进入带钢表面粗糙度轧制转印饱和阶段,且轧制转印后带钢表面粗糙度值达不到工作辊表面粗糙度值的100%.
综上,如图7 所示,由于工作辊表面轮廓算术平均偏差Ra与入口带钢表面轮廓算术平均偏差Ra存在不同大小的配比,导致不同工况条件下带钢表面粗糙度的遗传和演变规律也存在差异,具体有:

图7 平整轧制过程带钢表面微观形貌遗传和演变规律示意图Fig.7 Diagram of the inheritance and evolution of strip surface micromorphology in the process of flat rolling
当工作辊表面Ra>带钢表面Ra时,随着单位板宽轧制力的增大,带钢表面粗糙度先减小,然后增加,最后稳定,存在临界单位板宽轧制力使得带钢表面粗糙度最小,即达到负转印最大点;也存在临界单位板宽轧制力使得带钢表面粗糙度不再随单位板宽轧制力变化而变化,即达到轧制转印饱和点.
当工作辊表面Ra≈带钢表面Ra时,随着单位板宽轧制力的增大,带钢表面粗糙度先减小,再增加,最后稳定,但平整后带钢表面粗糙度不会大于入口带钢表面粗糙度,存在临界单位板宽轧制力使得带钢表面粗糙度最小,即达到负转印最大点;也存在临界单位板宽轧制力使得带钢表面粗糙度不再随单位板宽轧制力变化而变化,即达到轧制转印饱和点.
当工作辊表面Ra<带钢表面Ra时,带钢表面粗糙度逐渐减小到稳定,其负转印最大点和转印饱和点重合.
3 不同工艺参数对带钢表面微观形貌遗传和演变规律的影响
为更好地控制带钢表面微观形貌,明确不同工况条件下带钢表面微观形貌的遗传和演变规律,确定不同工况条件下带钢表面微观形貌负转印最大点以及转印饱和点对应的轧制力大小,本文仿真分析了带钢屈服强度的变化、入口带钢表面粗糙度的变化和工作辊表面粗糙度变化对带钢表面微观形貌的遗传和演变规律的影响,其中带钢屈服强度变化范围为100~900 MPa,入口带钢轮廓算术平均偏差变化范围为0.2~1.4 μm,工作辊轮廓算术平均偏差变化范围为0~3.5 μm.
3.1 工作辊表面粗糙度大于带钢表面粗糙度
工作辊轮廓算术平均偏差范围选取1.5~3.5 μm,入口带钢轮廓算术平均偏差范围选取0.6~1.4 μm,带钢屈服强度选取100~900 MPa,仿真计算如下:
(1)不同工艺参数对负转印最大点对应临界板宽轧制力的影响.
如图8(a)所示,当入口带钢表面粗糙度不变时,随着工作辊表面粗糙度的增大,负转印最大点对应轧制力逐渐增大.分析原因认为,如图9 所示的不同表面粗糙度电火花毛化工作辊二维轮廓支撑长度率曲线(tp代表对应于不同的轮廓水平截距时,轮廓支撑长度与取样长度之比,是评定表面微观不平度形状特性的一个参数),随着电火花毛化工作辊表面粗糙度增大,工作辊表面尖峰支撑长度所占比例增大,使得工作辊表面形貌挤压进入带钢表面更难,并导致负转印最大点对应的轧制力逐渐增大.

图8 工作辊Ra >带钢Ra 时不同影响因素对负转印最大点对应临界单位板宽轧制力的影响.(a)工作辊表面粗糙度;(b)入口带钢表面粗糙度Fig.8 Influence of different factors on the critical rolling force per unit width at the maximum point of negative transfer when work roll Ra >strip Ra:(a) surface roughness of the work roll;(b) surface roughness of inlet strip

图9 工作辊表面二维轮廓支撑长度率曲线Fig.9 Support length ratio curve of two-dimensional contour of work roll surface
如图8(b)所示,在工作辊表面粗糙度不变的情况下,随着入口带钢表面粗糙度增大,负转印最大点轧制力随之增大,分析原因在于入口带钢表面粗糙度增大,入口带钢表面微观形貌尖峰尺寸增大,导致工作辊表面微观形貌挤压进入带钢尖峰需要更大的轧制压力,引起负转印最大点轧制力的增大.
如图8 所示,当入口带钢表面粗糙度和来料带钢表面粗糙度不变时,随着带钢屈服强度的增大,负转印最大点对应轧制力逐渐增大.分析原因认为,当带钢屈服强度增大时,带钢表面粗糙峰较难发生塑性变形,工作辊表面粗糙峰挤压带钢表面粗糙峰需要更大的轧制压力,因此负转印最大点对应的轧制力会有所增大.
(2)不同工艺参数对转印饱和点对应临界板宽轧制力的影响.
如图10(a)所示,当入口带钢表面粗糙度不变时,随着工作辊表面粗糙度的增大,轧制转印饱和点对应的轧制力也增大.分析原因认为,当工作辊表面粗糙度增大时,工作辊表面微观形貌的尖峰和凹坑尺寸增大,完成全部转印即工作辊尖峰完全压入带钢且带钢金属产生塑性流动基本填充工作辊凹坑,此时需要更大的轧制力才能完成转印的全部过程.
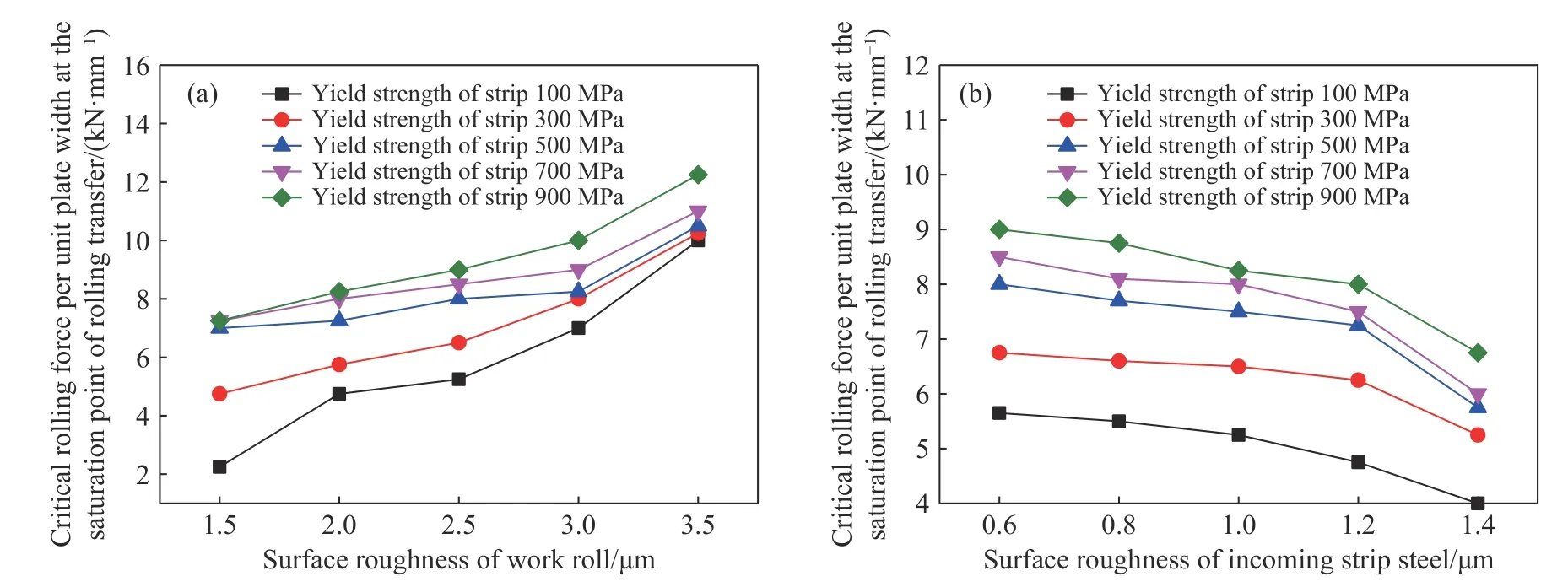
图10 工作辊Ra >带钢Ra 时不同影响因素对轧制转印饱和点对应临界单位板宽轧制力的影响.(a)工作辊表面粗糙度;(b)入口带钢表面粗糙度Fig.10 Influence of different factors on the critical rolling force per unit width at the saturation point of rolling transfer when work roll Ra >strip Ra:(a) surface roughness of the work roll;(b) surface roughness of inlet strip
如图10(b)所示,在工作辊表面粗糙度不变的情况下,随着入口带钢表面粗糙度值的增大,轧制转印饱和点对应轧制力略有下降.分析原因认为,当入口带钢表面粗糙度增大时,入口带钢表面的尖峰和凹坑增大,入口带钢表面形貌尖峰插入工作辊表面形貌凹坑的概率增多,减少了轧制转印过程带钢填充工作辊表面形貌凹坑的金属流动,使得带钢表面微观形貌达到转印饱和时所需的轧制力减小.
如图10 所示,当入口带钢表面粗糙度和工作辊表面粗糙度不变时,随着带钢屈服强度的增大,轧制转印饱和点所对应的轧制力略有增大.分析原因认为,当带钢表面微观形貌接近达到轧制转印饱和点时,需要带钢金属填充工作辊表面微观形貌的凹坑,当带钢屈服强度增大时,带钢金属塑性流动更加困难,引起轧制转印饱和点所对应的轧制力的增大.
3.2 工作辊表面粗糙度小于带钢表面粗糙度
工作辊轮廓算术平均偏差选择为0.5 μm,带钢轮廓算术平均偏差范围选取为0.6~1.4 μm,带钢屈服强度选取为100~900 MPa,进行仿真分析如下:
如图11 所示,在工作辊表面粗糙度不变的情况下,随着入口带钢表面粗糙度值的增大,轧制转印饱和点对应轧制力略有下降.分析原因认为,当入口带钢表面粗糙度增大时,入口带钢表面的尖峰和凹坑增大,入口带钢表面形貌尖峰插入工作辊表面形貌凹坑的概率增多,减少了轧制转印过程带钢填充工作辊表面形貌凹坑的金属流动,使得带钢表面微观形貌基本达到完全转印时所需的轧制力减小.

图11 工作辊Ra <带钢Ra 时不同影响因素对转印饱和点对应临界单位板宽轧制力的影响Fig.11 Influence of different factors on the critical rolling force per unit width at the saturation point of rolling transfer when work roll Ra 而随着带钢屈服强度的增大,轧制转印饱和点所对应的轧制力略有增大.分析原因认为,当带钢表面微观形貌接近达到轧制转印饱和点时,需要带钢金属填充工作辊表面微观形貌的凹坑,当带钢屈服强度增大时,带钢金属塑性流动更加困难,引起轧制转印饱和点所对应的轧制力的增大. 此时,需要注意的是,当工作辊轮廓算术平均偏差为0.5 μm 时,此时工作辊采用磨削加工,工作辊轴向与周向Ra值明显不同,轧后带钢轧制方向与板宽方向Ra值也明显不同,但不同工艺参数下的带钢表面微观形貌遗传和演变规律一致,仅存在绝对值的差异,此处不再赘述. 对于工作辊与带钢表面粗糙度接近的情况,选择带钢/工作辊轮廓算术平均偏差为1.0 μm/1.0 μm的情况进行仿真分析,探究带钢强度对轧制转印规律的影响. 如图12 所示,当工作辊与带钢表面形貌接近时,随着轧制力的逐渐增大,带钢表面粗糙度值会经历先下降、再上升、最后趋于稳定的过程,同时存在负转印最大点和转印饱和点.随着带钢屈服强度的增大,负转印最大点和转印饱和点对应的临界板宽轧制力明显变大,原因在于随着带钢屈服强度的增大,带钢表面发生塑性变形需更大的轧制力.同时对比发现,当带钢表面粗糙度与工作辊表面粗糙度接近时,无论带钢屈服强度如何变化,其负转印最大点对应轧后带钢表面最小粗糙度值基本一致. 图12 工作辊Ra=带钢Ra 时不同轧制力下带钢表面微观形貌的遗传和演变规律Fig.12 Inheritance and evolution of strip surface morphology under different rolling forces when work roll Ra=strip Ra (1)基于大量现场实测,获得了不同粗糙度工作辊与带钢表面的真实二维轮廓,建立了工作辊与带钢真实粗糙表面接触的表面微观形貌轧制转印生成模型.依托工业现场展开试验,实测得到带钢表面的Ra、Rz、Ry和Pc值,并与模型计算结果进行对比,计算值与实测值最大相对误差在10%以内,验证了仿真模型的准确性. (2)利用模型分析带钢表面粗糙度小于、等于和大于轧辊表面粗糙度三种情况下,带钢表面微观形貌的轧制转印行为与遗传演变规律,提出负转印和转印饱和的概念,定义了两种极限轧制转印状态的描述指标——负转印最大和转印饱和来表征带钢表面微观形貌的遗传和演变.通过计算发现,当带钢表面粗糙度小于或等于轧辊表面粗糙度时,随着单位板宽轧制力的增大,带钢表面粗糙度都存在先减小再增加的趋势,对应存在负转印最大点和转印饱和点;而当带钢表面粗糙度大于轧辊表面粗糙度时,随着单位板宽轧制力的增大,带钢表面粗糙度逐渐减小到趋于稳定,对应的负转印最大点和转印饱和点重合. (3)采用前述定义的两种极限轧制转印状态描述指标,分析带钢屈服强度、带钢表面粗糙度以及轧辊表面粗糙度对负转印最大点和转印饱和点对应的临界单位板宽轧制力的影响规律,发现随着带钢屈服强度的增加,负转印最大点和转印饱和点对应的临界单位板宽轧制力逐渐增大;随着轧辊表面粗糙度增加,负转印最大点和转印饱和点对应的临界单位板宽轧制力也逐渐增大;随着带钢表面粗糙度增加,负转印最大点对应的临界板宽轧制力增大,而转印饱和点对应的临界板宽轧制力减小.3.3 工作辊与带钢表面粗糙度接近

4 结论
