河北地方性震级量规函数与方位角校正值研究1

王亚玲 毛国良 周 依 王 宁 蒋宏毅

（河北红山巨厚沉积与地震灾害国家野外科学观测研究站, 石家庄 050000）

引言

震级是衡量地震大小的物理量，是地震三要素之一，也是地震研究、预测及抗震救援决策等相关领域重要的数据支撑（许德相等，2015），另外，随着预警系统部署、发展，对近震震级精准度有着更高的要求，因此有必要对震级校正进行研究。

震级测定会因传播途径、台站台基、量规函数、仪器等方面的影响，存在一定误差（陈培善等，1983）。李军等（2016）的研究表明介质传播方向会影响震级精确度。近年来，关于方位角对震级测定的影响研究及校正取得了众多成果，如魏贵春等（2017）对数字测震单台不同方位震级进行了统计研究，结果表明对不同方位地震测定的震级偏差进行相应校正是必要的。自2001 年10 月河北测震台网数字化后，其记录了大量地震事件数据，很多关于河北台网台基、仪器、测量方法等方面的研究成果相继产出，如李雪英等（2004）、张从珍等（2005）、赵明淳等（2005）主要对量规函数及台基进行了校正，较少涉及对震源方位角影响及校正的研究。本文基于河北省测震台网产出资料，在量规函数校正的基础上分析单台数字测定的地方震震级偏差与方位角的关系，为更精准测定震级提供数据支撑，也为预警震级的测定提供相关数据依据。

1 数据选取与处理

1.1 数据选取

考虑数据量及时效性问题，选取近5 年测震台网数据，因此本文基于2016-2020 年河北测震台网记录的941 次ML≥2.0 天然地震事件（图1）中的21 049 个单台记录地震数据进行统计分析。

图1 所选地震事件震中分布Fig.1 Epicentre distribution of selected seismic events

1.2 计算方法

震级测定的主要依据是对数字波形进行W-A（伍德-安德森）仿真，然后选取S/Lg（S 波为地震产生的横波/Lg 波为震中距在10 度至20 度之间的地震，监测到一种在S 波之后到达，频率较高，可持续几个周期的面波。）上最大的振幅值（刘瑞丰等，2007，2018a，2018b），计算公式为：

式中，Aμ为 地动位移（单位μm），Aμ=(AN+AE)/2；AN、AE分别为NS、EW 分向的S 波或Lg 波位移最大幅值；Δ 为震中距；R(Δ)为量规函数。

由式（1）计算地震事件的各单台震级，并计算地震事件的台网平均震级MLn。

根据式（2）可计算得到第n个地震事件的第m个子台震级偏差值ΔMLnm：

式中，MLnm为第n个事件第m个子台震级。

最后，利用式（3）和式（4）分别计算第m个子台记录的地震事件的单台震级平均偏差ΔMLm及标准偏差δm：

式中，P为单台记录地震总数。

基于上述公式计算分析选取的地震事件单台震级平均偏差及标准偏差，结果如表1 所示。根据计算结果统计单台震级偏差 ΔMLnm频次，如图2 所示。由表1 和图2 可知，震级偏差整体较符合正态分布，其中|ΔMLnm|≤0.2 的记录12 366 个，占比为58.74%，震级偏差值集中，表明现有量规函数校正效果显著。但随着近年来仪器的更换、台站的增加，现有量规函数表现出一定的不适应性，主要表现为部分台站震级偏差较大，因此对原始量规函数进行校正有一定的必要性。

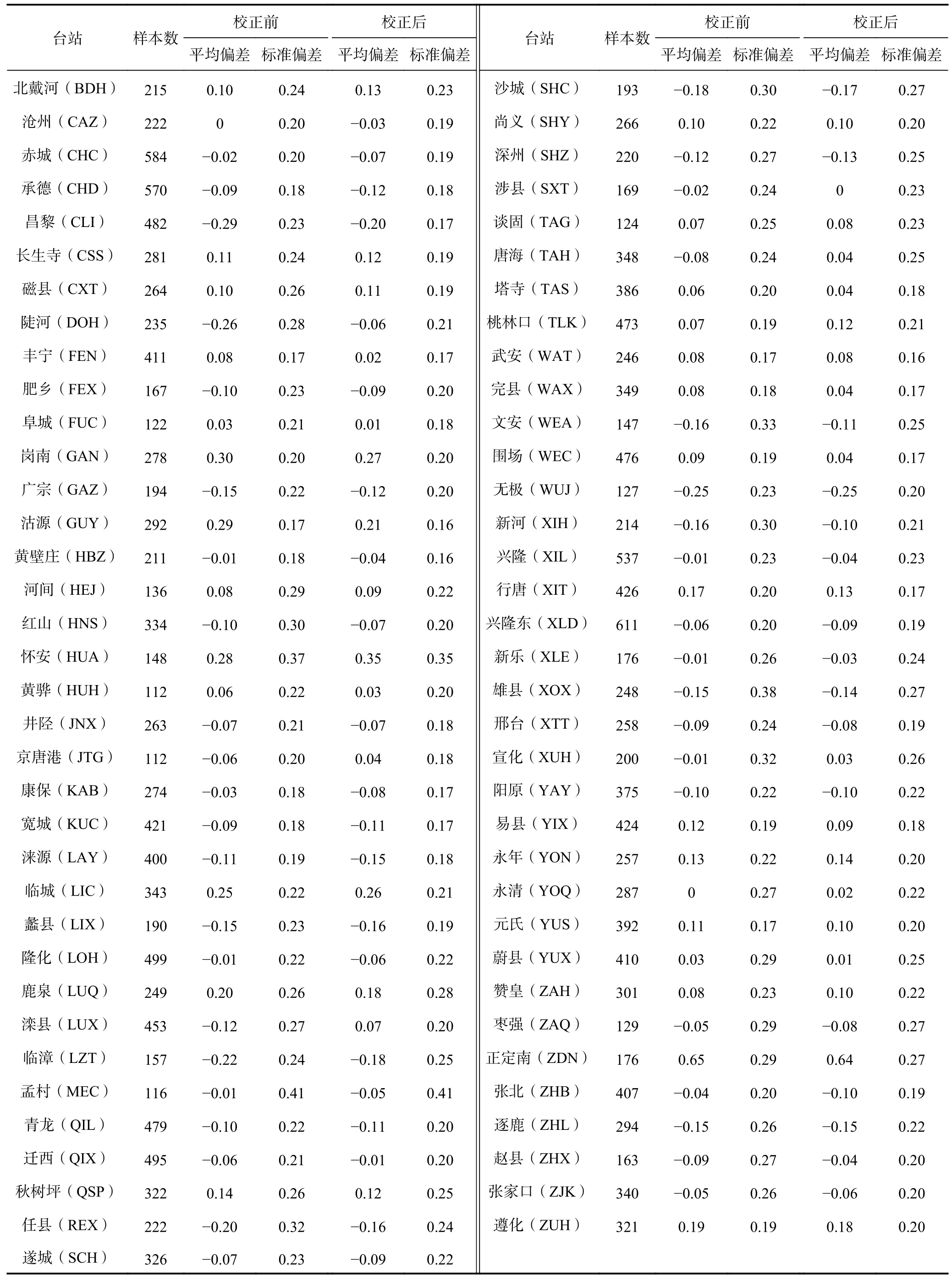
表1 各单台震级平均偏差及标准偏差Table 1 Mean deviation and standard deviation of each seismic magnitude

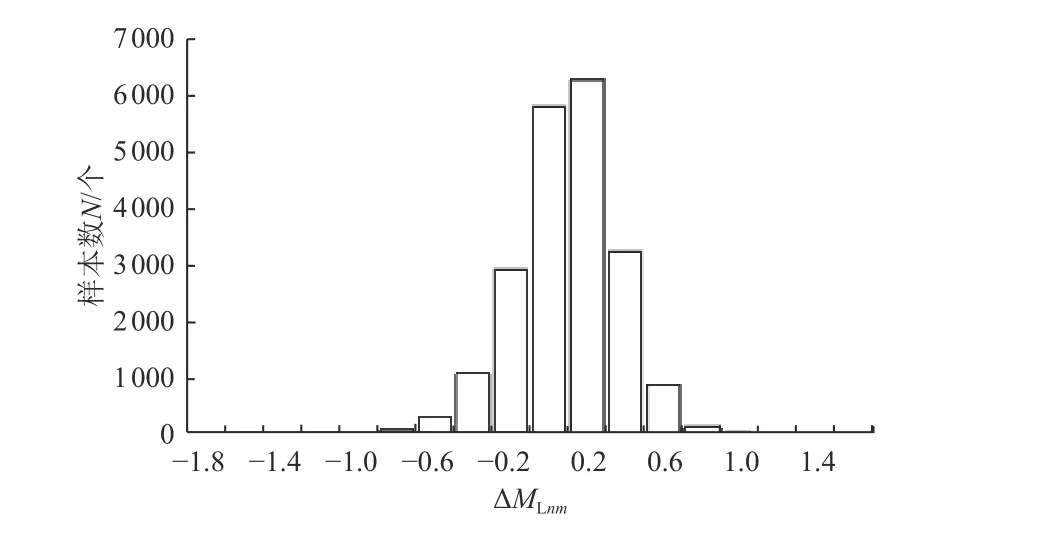
图2 原始震级偏差统计Fig.2 Original magnitude deviation statistics

2 量规函数校正

2.1 计算方法

本文选取的数据资料震中距为0～757 km，考虑数据样本量，本文将 Δ＜490 km 的震中距补充主语以5 km 为区间划分为98 个区段，由式（5）计算每个区间的单台震级偏差的平均值 ΔMb，结果如表2 和图3所示。

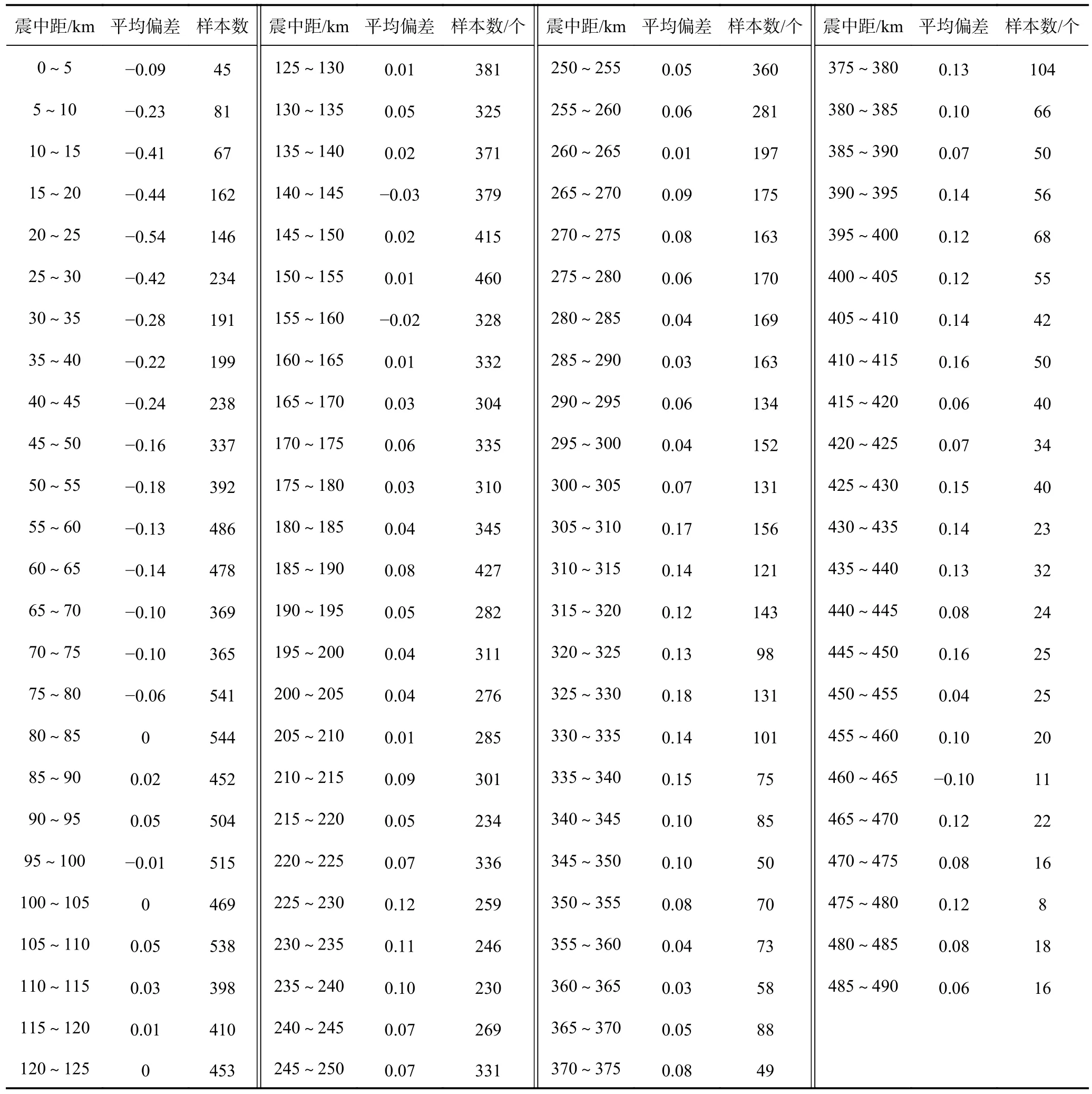
表2 按震中距分段统计震级平均偏差Table 2 Average deviation of earthquake magnitude according to epicentral distance

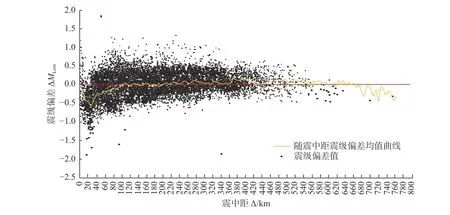
图3 单台震级偏差随震中距的变化Fig.3 Variation of magnitude deviation of single station with epicenter distance

式中，b为间隔数；N为间隔范围内震级偏差样本。

由表2 和图3 可知，当震中距为0～80 km 时，震级平均偏差＜0，尤其在震中距10～30 km 时平均偏差均小于-0.40，说明在此震中距范围内量规函数值偏小，稳定性较差，震级平均偏差波动性大；在震中距80～225 km 和240～305 km 时，震级平均偏差绝对值均较小，说明量规函数较适用；当震中距为225～240 km、305～415 km、425～440 km 时，震级偏差平均值均大于0.10，说明此区间的量规函数值偏大，稳定性不够；震中距在440～490 km 区间时震级平均偏差既有正值又有负值，说明此区间的量规函数不稳定。

2.2 量规函数校正

依据上述规律取表2 中的负值对量规函数进行校正，根据校正后量规函数计算71 个单台测定的震级偏差平均值，如表1 所示，校正后单台偏差ΔMLnm频次分布如图4 所示，并据此得到河北区域校正量规函数，如图5 所示。

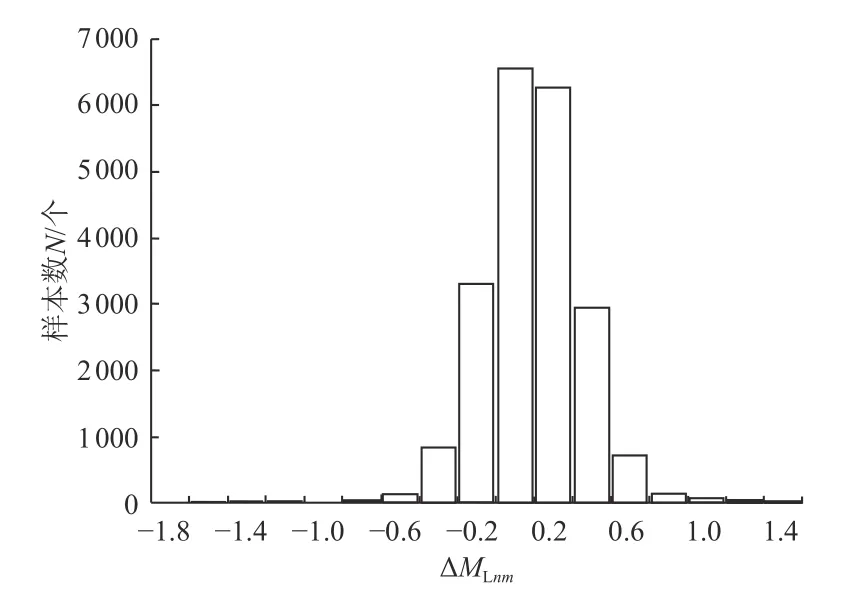
图4 量规函数校正后震级偏差频率Fig.4 Magnitude deviation frequency after calibration of gauge function

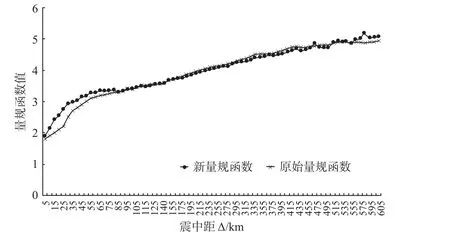
图5 量规函数校正前后对比Fig.5 Comparison of gauge function before and after calibration

由表1 可知，经量规函数校正后，71 个单台中37 个台站的震级偏差明显降低，28 个台站震级偏差稍有上升，6 个台站震级偏差没有变化。对比图2 和图4 可知，经校正后的单台偏差ΔMLnm频 次更集中，|ΔMLnm|≤0.2 的样本数上升至13 093 个，占比提升至62.20%，说明校正后量规函数对震级偏差校正效果更明显；对于校正后的标准偏差值，除5 个台站有所上升、6 个台站保持不变外（图6），其余台站均有所下降，说明经量规函数校正后震级偏差值离散程度得以收敛，因此校正后量规函数更适合本地区使用。

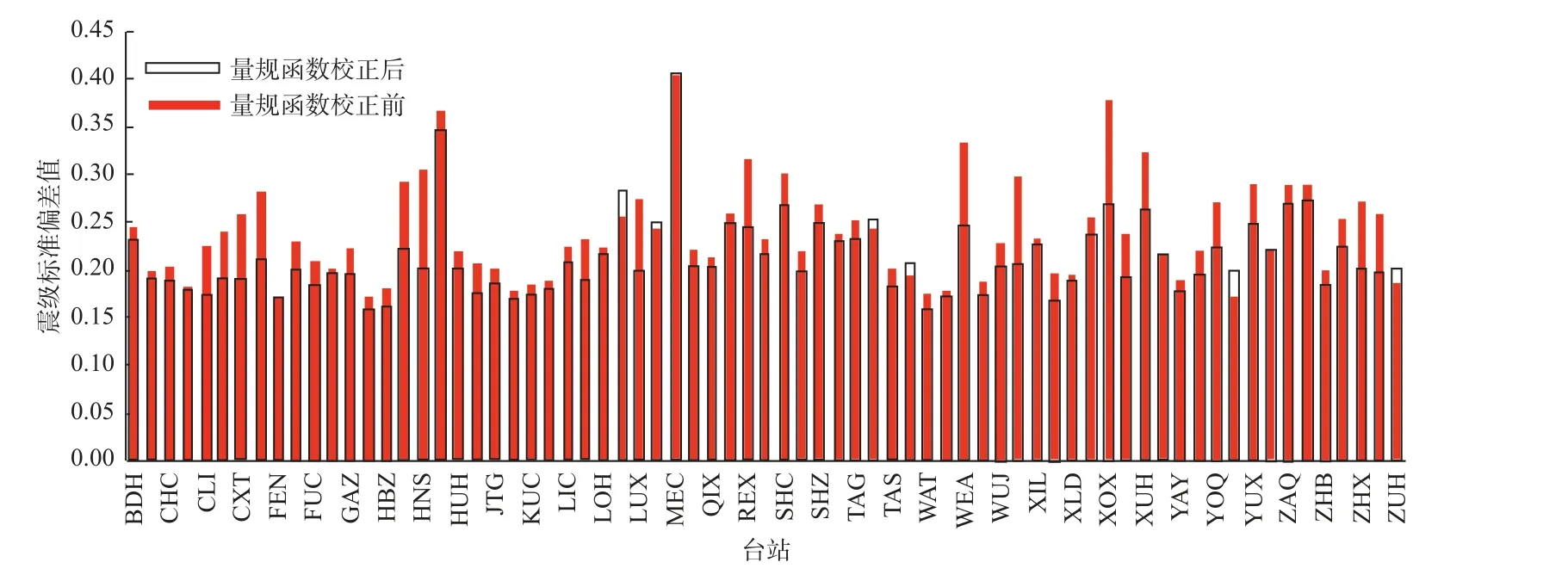
图6 量规函数校正前后单台震级标准偏差值对比Fig.6 Comparison of standard deviation values of single earthquake magnitude before and after calibration of gauge function

3 不同方位震源震级影响

对于同一台站来说，不同方位传递的地震波能量衰减系数存在不一致性，原因在于地震波能量辐射具有方向性。

3.1 计算方法

基于选取的地震数据，将71 个单台不同方位震源按30°划分为12 个扇形区域（魏贵春等，2017），按照上文规律对划分的每个扇形内记录的地震数据进行量规函数校正，然后基于式（6）计算得到不同方位震源数据的震级平均偏差值 ΔMLG：

式中，ΔMLr为第L个地震事件的第r个子台震级偏差值；N为不同方位角区间样本数量。

3.2 计算结果

71 个台站依据不同方位震源产生的震级偏差各异，结果如图7 所示，但同一区域的台站变化规律表现出相对的一致性。

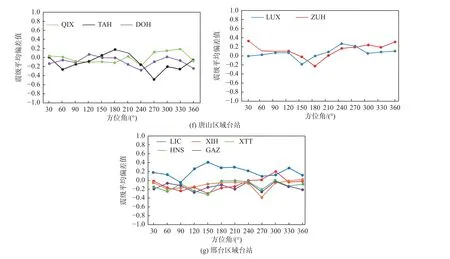
图7 台站震级平均偏差值随方位角变化趋势Fig.7 The variation trend of the mean magnitude deviation of the station with the azimuth angle

（1）石家庄地区：如图7（a）所示，赵县、元氏、赞皇、井陉、谈固台站不同方位震源震级变化趋势呈现一定的规律性，但黄壁庄台站因受到水库影响，在方位角为60°～150°时震级平均偏差值变化明显，分别在方位角为90°、120°处达到低值峰-0.48 和高值峰0.48，其余区间震级平均偏差值变化趋势与区域内其他台站相似；正定南台站震级平均偏差值较大（＞0.2）且均为正值，说明不同方向震源不是正定南台站震级的主要影响因素，推测可能是土层放大效应的影响；无极台站震级整体偏小，通过对数据的进一步分析发现震级大小及每个区间震中距对震级平均偏差值无规律性影响，但无极台站位于无极-衡水断裂附近，推测可能与其地质条件相关；岗南、行唐台站震级整体偏差值较小，大部分区间内偏差绝对值＜0.2，变化趋势不明显。

（2）邯郸地区：如图7（b）所示，此区域内震级平均偏差值整体变化规律不明显，在方位角为180°～240°时震级平均偏差值先上升后下降，在方位角为180°时达到峰值；磁县台站在方位角为60°～120°时震级平均偏差值下降幅度较大且均＜0，推测此区间内的震源在经过峰峰矿区会对地震波能量起到衰减作用，导致震级偏差值偏小；临漳台站震级平均偏差值变化幅度较大，在方位角为120°时达到峰值，震级整体偏差值偏小。

（3）承德地区：由图7（c）可知，宽城、兴隆东、兴隆、围场、隆化台站单台震级平均偏差值随方位角增大的变化趋势具有较高的相似性，在方位角＜180°时的震级偏差值整体存在减小趋势。除兴隆东台站外，均在方位角为180°～240°时震级平均偏差值呈上升趋势，且在方位角为240°～270°时震级平均偏差值呈下降趋势。对于方位角＞270°时，除隆化台站外，其余单台震级平均偏差值表现出先增大后减小的趋势。另外承德台站、丰宁台站震级平均偏差值变化规律不明显，整体浮动较小，表明受到不同方位震源的影响较小。

（4）张家口地区：涿鹿、张北、沙城、赤城台站在方位角为30°～120°时震级平均偏差值先下降后上升，如图7（d）所示，并在方位角为90°处出现低值峰，震级平均偏差值在方位角为120°～360°时在-0.2～0.2之间波动，起伏较小；怀安台站整体震级偏差值偏大，均＞0，说明该台站不同方位震源的影响较小，经过对资料进行梳理分析，发现怀安台站北西侧有河流，推断在方位角＜180°时震级偏大可能受该因素影响。

（5）秦皇岛地区：如图7（e）所示，桃林口、昌黎、青龙台站震级平均偏差值变化趋势不明显，受不同方位震源的影响较小，在方位角＜150°时震级平均偏差值整体呈先减小后增大的趋势；在方位角为150°～240°时震级平均偏差值基本不变，此区间内方位角的影响程度相对一致；在方位角为270°～300°时震级平均偏差值几乎为0，说明此区间内3 个台站受不同方位震源的影响可忽略不计。

（6）唐山地区：由图7（f）可知，滦县、遵化台站整体震级平均偏差值随方位角变化相似性较小；迁西、唐海、陡河台站在方位角＜150°的区间内震级平均偏差值整体浮动较小，受方位角的影响较小，在方位角为150°～240°区间内震级平均偏差值呈先上升后下降的趋势；在方位角为150°～360°区间内迁西台站与陡河台站震级平均偏差值变化趋势具有较大的相似性，均为先上升后下降，此区间内的唐海台站受潮汐影响震级偏差值变化较大。

（7）邢台地区：如图7（g）所示，区域内的红山、新河、广宗、邢台台站在方位角＜240°、300°～360°时震级平均偏差值均波动不明显，在方位角为240°～300°时震级平均偏差值均呈先减小后增大的趋势；临城台站在方位角＜180°时震级平均偏差值起伏较大，在方位角为180°～240°时震级平均偏差值可忽略不计，在方位角为240°～300°时震级平均偏差值呈先下降后上升的趋势，在方位角为300°～360°时震级平均偏差值呈先上升后下降的趋势，依据统计的资料数据无法解释该台站所有方位震级平均偏差值均大于0，通过调查发现临城台站位于河流旁边，推测与该因素产生的影响有关。

本文计算了71 个台站随方位角变化的震级平均偏差值，但有些台站分布疏散，震级偏差值变化趋势较复杂，本文着重分析分布相对集中的48 个台站，根据结果可知方位角对震级偏差的影响虽具有复杂性，但有一定规律可循，48 个台站中有36 个台站在方位角为180°～240°的区间内震级偏差值表现为先上升后下降的趋势，具体原因尚需进一步深入分析。现有的地震事件定位方法是利用包围震中的不同方位台站进行定位，得到各台站平均震级，削弱了震源辐射方位的影响。

3.3 方位角校正

依据图7 可知方位角对近震震级测定产生了一定影响，统计分析测震台站各方位角区间内的地方震震级平均偏差值如表3 所示，共给出了852 个区间，除去53 个空值区间及样本数量为1 的无法计算平均值的47个区间，其余752 个区间的震级偏差值为-0.86～0.80，其中|ΔMLnm|≤0.2 的区间有526 个，占比为69.95%，剩余30.05%的区间震级偏差值＞0.2，说明方位角偏差值影响较大，有校正的必要性。本文取表3 中的负值作为校正值，校正后得到的台站震级偏差值有所下降，根据统计得到方位角震级偏差值校正后的震级偏差频次ΔMLnm，如图8 所示。

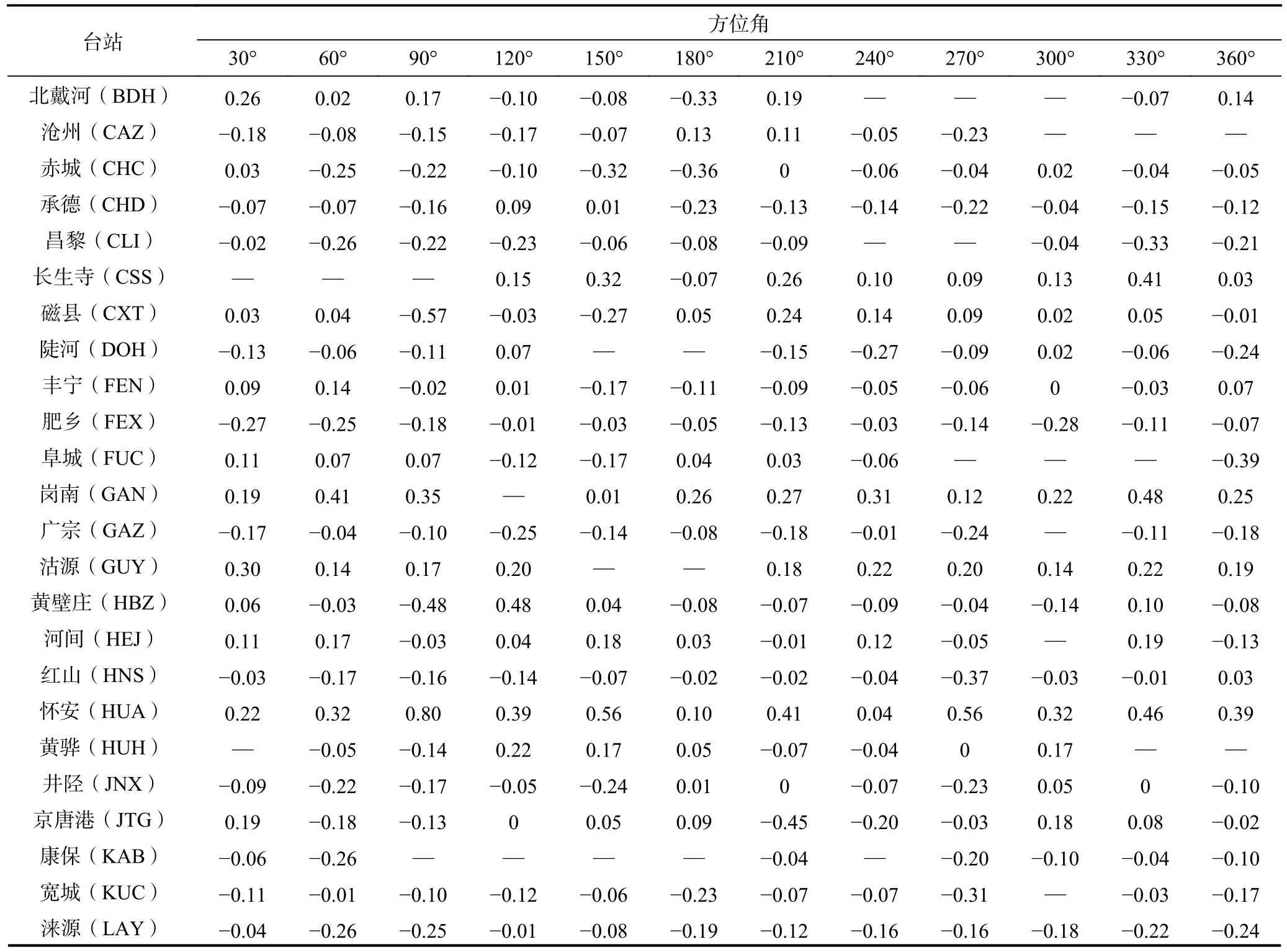
表3 71 单台站不同方位震源震级偏差统计表Table 3 71 Statistical table of source magnitude deviation at different directions at a single station

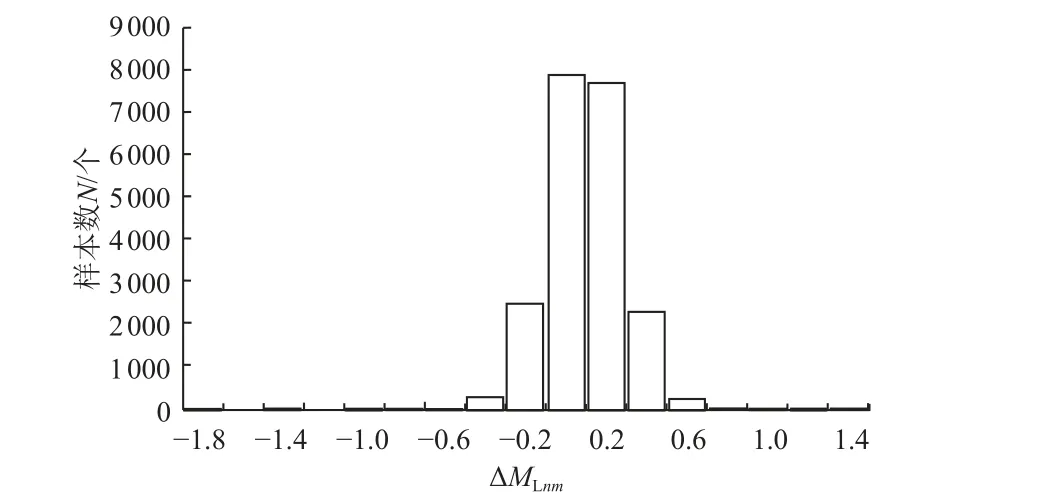
图8 方位角校正后震级偏差频率Fig.8 Magnitude deviation frequency after azimuth correction

根据统计结果，方位角校正后|ΔMLnm|≤0.2 的单台震级偏差有15 739 个，占比由量规函数校正后的62.20%提升至74.77%，说明方位角偏差值校正结果使震级偏差频次更收敛，校正效果明显，因此对方位角进行校正具有一定的必要性。

4 结论

由上述结果分析可知，震级测定精度受多种因素的影响。本文主要从量规函数、方位角等方面，采用统计分析、对比等方法对各单台震级偏差进行分析校正，得出以下结论：

（1）对于量规函数校正，针对选取的数据资料，统计分析地震事件中单台测定的震级偏差随震中距变化规律，当震中距＜80 km 时，震级偏差均为负值，尤其在10～30 km 内平均偏差均＜-0.40，说明此震中距范围内原量规函数值明显偏小；震中距为80～225、240～305 km 时，量规函数较适用于本地，震级平均偏差整体偏小；震中距为225～240、305～415、425～440 km 时，震级平均偏差值均＞0.10，说明此区间的量规函数值偏大。根据上述规律对量规函数进行校正，拟合得到更适合河北地区的区域量规函数。

（2）基于2016-2020 年河北测震台网记录的941 次ML≥2.0 级地震事件，将71 个单台不同方位震源按30°划分为12 个扇形区域，因地震分布不均匀性导致出现53 个空值区间及样本数量为1 的47 个区间，此类区间不参与计算震级平均偏差值。计算752 个区间结果显示，震级偏差值|ΔMLnm|≤0.2 的区间有526 个，占比为69.95%；71 个台站不同方位震源产生的震级偏差变化趋势明显各异，但同一区域的台站变化规律表现出相对的一致性，结果如图7 所示。经校正后各区间震级平均偏差值有所下降，|ΔMLnm|≤0.2 样本数提升至74.77%，说明方位角校正有必要且有意义。

综上所述，河北测震台网单台测定震级大多数是有偏差的，对此，现有地方震级计算公式中已考虑量规函数、台基校正等方面的影响。本文进行量规函数校正后，发现对于发生在不同方位的地震事件，由于传播路径介质不同，存在着区域性差异，根据各区间震级平均偏差值进行方位角校正，震级偏差值|ΔMLnm|≤0.2样本数有明显提升，因此方位角校正对于提高震级计算精度具有一定意义。对于消除因方位角产生的震级影响，还需进一步研究。

由于资料限制，地震分布不均匀，导致台站的部分方位区间内样本数量偏少，因此本文阐述的规律存在一定局限性，需进一步深入研究。