小间距平行顶管管道土压力计算方法研究
2021-10-23肖宇锋黎永索
杨 仙,肖宇锋,黎永索,陈 娟
1) 湖南科技大学资源环境与安全工程学院,湘潭 411201 2) 湖南城市学院市政与测绘工程学院,益阳 413000 3) 湖南科技大学信息与电气工程学院,湘潭 411201
作为一种环境影响小、综合成本低、施工周期短的非开挖工法,顶管法在交通运输、市政工程以及大型综合性地下空间的开发利用中都得到了广泛的应用[1−3].随着城市地下建(构)筑物越来越密集,地下空间的有限性迫使小间距的双线、甚至是多线顶管工程越来越多[4−5].同时,在一些新型的管幕类地下工程暗挖工法(如管幕预筑法[6−7]、管幕冻结法[8−9]和管幕箱涵法[10−11]等)中,小间距多管顶进也是其关键施工步骤.由此可见,随着社会经济的进一步发展,以及国家地下空间开发政策的逐步实施,小间距顶管工程将会越来越多.
顶管工程中,管道所受到的最大荷载主要来自于其上部土体重力,因此在顶管设计中,正确计算管道竖向土压力至关重要.土压力的计算结果,直接影响顶管工程中荷载确定、结构计算及顶力估算与控制等重要设计施工因素,从而影响后背墙体的设计、顶推设备的确定、管道强度选择以及中继间布设等涉及安全性和经济性的重要问题.常用的管道土压力计算理论有土柱理论、普氏土拱效应理论及太沙基松动土压力理论[12−13]等.郭文赓[14]比较了84 项顶管工程实测结果与计算结果,认为太沙基理论土压力计算符合率达74.5%.诸多文献基于现场实测及理论分析,对太沙基理论中土体松动线[15−17]及侧压力系数[18−20]等进行了探讨和改进.我国及美国、德国、日本等国家的顶管工程技术规范[21]中,也都采用了太沙基或修正的太沙基理论计算管道土压力.
对于小间距顶管工程,已有较多关于地表沉降计算方法[22−24]的研究,但对于小间距顶管管道土压力计算方法方面的研究还很少见.部分学者基于模型试验[25],结合复变函数理论、解析延拓法和 Schwarz 交替法的理论方法[26],分析了岩体中无支护条件的水平并行隧道围岩应力分布特征,但其与一般位于浅层土体中的小间距平行顶管工程土压力分布有着本质区别.小间距平行顶管工程中,由于管群−土体之间相互作用的影响[27−28],管道土压力分布模式与单管顶进时产生了很大差异,但目前小间距平行顶管工程中的土压力计算仍参考既有单管顶进规范来进行,完全未考虑管群−土体之间的相互作用.
本文考虑管−管相互作用的影响,结合数值模拟反分析,基于太沙基土压力理论和土体极限平衡理论,假设了土体松动线和上部既有顶管支挡作用线,并进一步构建了小间距平行顶管管道土压力理论计算方法,采用此方法分析了顶管管径、管间距、土体力学参数等对小间距平行顶管管道土压力的影响,并与不考虑既有顶管影响的土柱理论和太沙基土压力理论计算结果进行了对比分析.
1 理论计算方法假设条件的提出
如图1 所示,以平行两小间距顶管(等直径,上下排列)为例,来建立后顶进顶管(下部顶管,后文简称新建顶管)受先顶进顶管(上部顶管,后文简称既有顶管)支挡作用影响下,新建顶管拱顶垂直土压力的计算方法.

图1 小间距平行顶管土压力计算示意图Fig.1 Schematic of earth pressure calculation of parallel pipe jacking with small spacing
太沙基土压力计算理论由Terzaghi[12]于1936 年基于活动门实验提出,其经过了大量隧道工程实践的验证,目前广泛应用于单管顶进拱顶土压力计算中.太沙基理论认为,地层中的工程活动导致其上一部分土体发生屈服,而周围的土体保持不动.屈服土体向下位移的过程中,在与周围稳定土体的分界面上受到剪切阻力,因此地下结构受到的垂直土压力实际小于土柱压力(土柱压力理论认为垂直土压力为土体自重).且太沙基理论假设了松动土体的范围:如图1 中AFN为太沙基松动线,左右两边松动线对称;RN为圆O2的切线,FN与水平线夹角为(π/4+φ/2)(φ为土体内摩擦角,如图1 所示),AF为垂直线.其后,又有诸多学者对土体松动范围提出了改进意见[15−17],但太沙基松动线应用最为广泛.本文计算新建顶管造成的松动范围,仍沿用太沙基松动线.
小间距平行顶管工程中,由于既有顶管的存在,其对土体向下的位移产生支挡效应,导致新建顶管拱顶土压力与单管顶进时产生了较大的差异.本文建立的管道土压力计算方法在考虑周围稳定土体对向下位移土体的剪切阻力之外,还考虑了既有顶管的支挡效应.本文建立的新建顶管拱顶土压力计算方法存在两个假设条件:(1)既有顶管的存在对其上的部分土体形成支挡,保证了该部分的稳定性,新建顶管施工过程中,既有顶管上部被支挡的部分不向下发生位移.(2)新建顶管拱顶土压力为既有顶管底部的应力与两管间所夹土体的重力之和,也即忽略两侧边松动土体对新建顶管拱顶土压力的影响.
采用Midas 软件进行了两大直径钢管小间距平行顶进数值模拟.数值模拟建立的地层模型整体尺寸为10 m × 10 m × 30 m(水平方向×竖直方向×纵向延伸方向),顶管上下平行排布,上部顶管管道中心的埋深为3.6 m,下部顶管管道中心的埋深为6 m,管道直径为2 m,管道厚度为18 mm.地层采用摩尔−库伦模型,钢顶管采用弹性模型,材料力学参数如表1 所示.

表1 数值模拟材料力学参数Table 1 Mechanical parameters of the materials in numerical simulation
图2 为数值模拟云图.由图2(a)中数值模拟竖向位移云图可以看出,既有顶管拱顶存在蓝色部分,其为位移极小区,验证了假设条件(1).基于土体极限平衡理论,如图1 所示,假设既有顶管支挡线(GI、GH)与既有顶管相切,且与水平面的夹角为(π/4+φ/2)(φ为土体内摩擦角),两条支挡线之间的土体即为既有顶管上部的稳定土体.被支挡的土体(图1 中GIH部分)不会产生向下的位移趋势,同时因黏聚力与摩擦力的存在,对周围松动土体产生向上的挟持力.
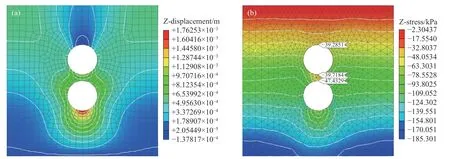
图2 数值模拟云图.(a)竖向位移云图;(b)竖向正应力云图Fig.2 Cloud images of (a) vertical displacement and (b) vertical normal stress from numerical simulation
由图2(b)数值模拟竖向正应力云图可知(该图中标注的三个数值是Midas 软件查询出的该点竖向应力值,单位kPa,下文中提到查询出的应力值时只保留了一位小数):既有顶管拱顶应力(39.3 kPa)和底部应力(39.7 kPa)基本相等,既有顶管底部的应力与两管间所夹土体的重力之和基本等于新建顶管拱顶应力(47.4 kPa),验证了假设条件(2).拱顶稳定部分的重力及其对周围土体挟制力的反力,造成了既有顶管拱顶的土压力;因薄壁钢管重力及钢管管壁对周围松动土体摩擦力的反力均很小,因此既有顶管拱顶和底部应力基本相等.同时,两侧松动土体传递到新建顶管拱顶的力极小,因此新建顶管拱顶土压力基本等于既有顶管底部的应力与两管间所夹土体的重力之和.
由上述分析可知,数值模拟计算结果验证了两个假设条件的合理性.最终采用本文构建的理论方法计算出的本案例中新建顶管拱顶土压力为48.8 kPa,稍大于数值模拟结果(47.4 kPa),也进一步验证了假设条件及本文所构建计算方法的合理性.
2 新建顶管拱顶土压力计算方法
(1)AB段土压力计算.
AB段中,松动部分的微元体两侧受到太沙基松动线外稳定土体的摩擦力和黏聚力.AB段中取微元体进行受力分析,如图3 所示.
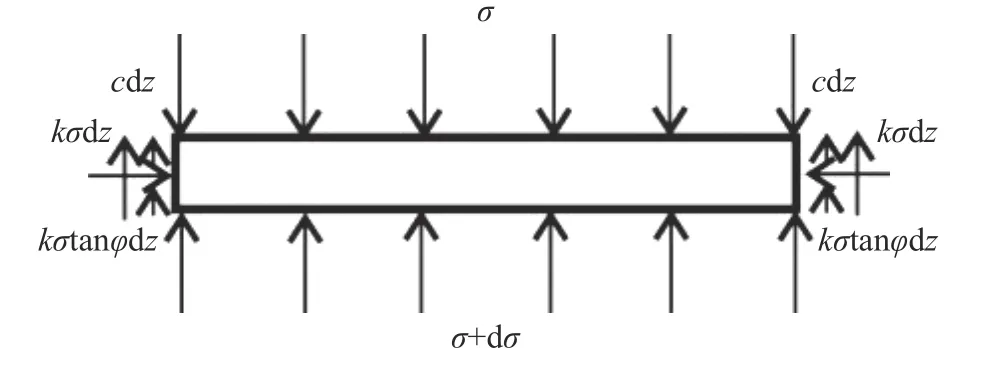
图3 AB 段微元体受力示意图Fig.3 Schematic of force on the micro-element in the AB segment
根据太沙基理论:
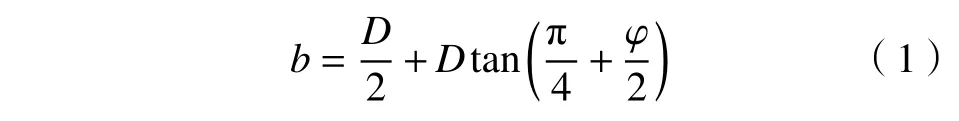
B点的纵坐标为:
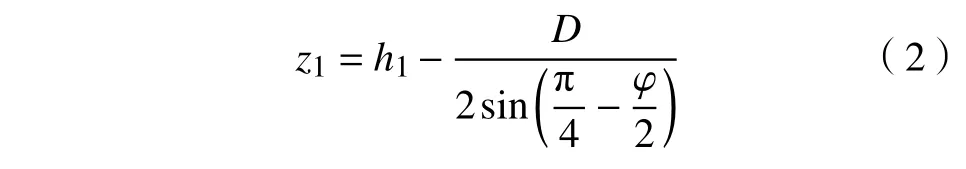
对微元体列平衡微分方程:
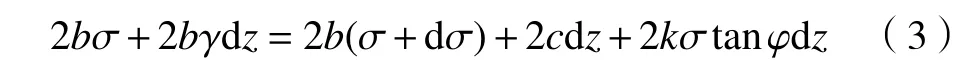
其中,b为土体松动部分计算宽度的一半(即图1中OA长度),m;D为顶管直径,m;φ为土体内摩擦角,°;c为土体黏聚力,kPa;γ为土体重度,kN·m−3;h1为既有顶管中心纵坐标值,m;dz为微元体的高度,m;k为太沙基土压力理论中土的侧压力系数,取值范围在0.5~1 之间[18−20];σ为AD段中微元体受到的垂直土压力,kPa;dσ为AD段中微元体受到的垂直土压力增量,kPa.
方程(3)的初始条件为地表土压力为0,即z=0时,σ=0.把初始条件代入方程,即可得到AB段中任意深度时的垂直土压力.
(2)BC段土压力计算.
BC段中,松动部分的微元体一侧受到太沙基松动线外土体的摩擦力和黏聚力,另一侧受到被既有顶管支挡的稳定土体的摩擦力和黏聚力.微元体受力分析如图4 所示.
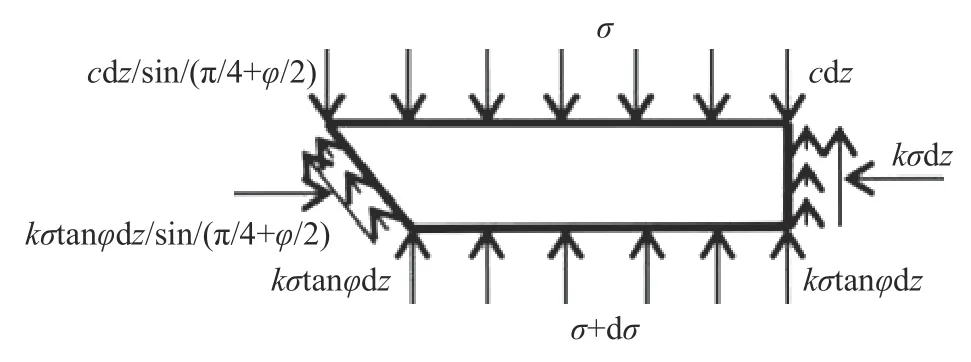
图4 BC 段微元体受力示意图Fig.4 Schematic of force on the micro-element in the BC segment
C点的纵坐标为:
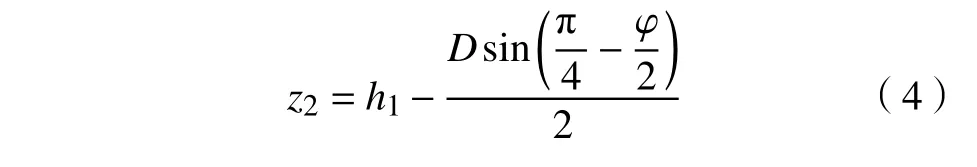
BC段微元体上底的长度为:

下底的长度为:

对微元体竖直方向列平衡方程,得到:
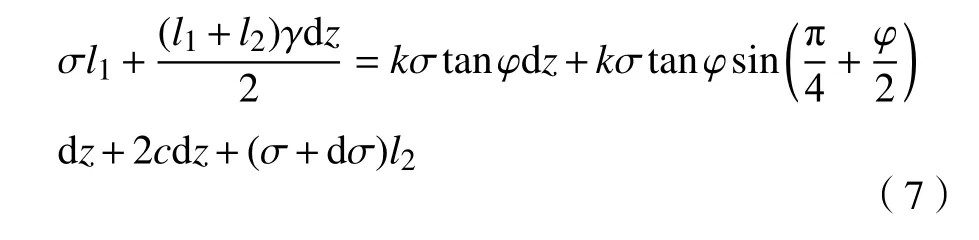
AB段中B点的土压力计算结果即为本段微分方程的初始条件.把初始条件代入方程(7),即可得到BC段中任意深度时的垂直土压力.BC段每一个微元体受到与之接触的GIH段(图1 所示)微元体的向上的挟制力,该挟制力也可根据方程(7)及初始条件得出,从而可得到GIH段微元体受到的向下挟制力的反作用力.
(3)CD段土压力计算.
CD段中,松动部分的微元体一侧受到太沙基松动线外土体的摩擦力和黏聚力,另一侧与顶管管壁接触,管壁无黏聚力,只提供摩擦力.微元体受力分析如图5 所示.
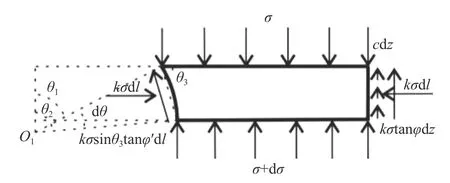
图5 CD 段微元体受力示意图Fig.5 Schematic of force on the micro-element in the CD segment
由图5 可得:
CD段微元体上底的长度为:
下底的长度为:
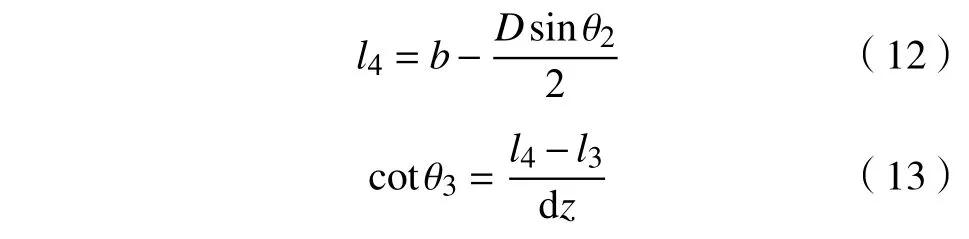
对微元体列竖向平衡方程得到:
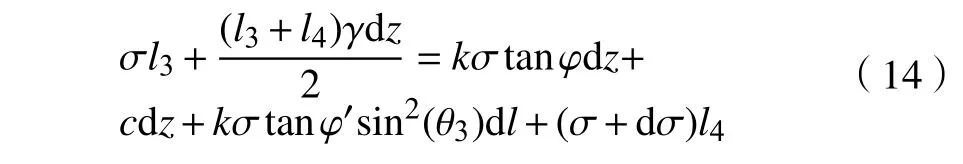
其中,θ1为微元体与顶管管壁上接触点与圆心O1连线和竖直线的夹角,°;θ2为微元体与顶管管壁下接触点与圆心O1连线和竖直线夹角,°;θ3为微元体对应的弦与上底的夹角,°;dl为微元体与顶管管壁接触弧长,m.
φ′为土体与顶管管壁接触的内摩擦角,°.参照南京库仑软件技术有限公司出版的《GEO5 用户手册》,根据结构表面的粗糙程度,该参数的大小通常为土体内摩擦角的1/3~2/3 之间.实际计算过程中,管周润滑情况一般时,若为混凝土管则取土体内摩擦角的2/3,若为钢管则取土体内摩擦角的1/3,若既有顶管管周泥浆套保持完整,润滑情况良好,则可忽略管土之间的摩擦力.
BC段中C点的土压力计算结果即为本段微分方程的初始条件.把初始条件代入方程(14),即可得到CD段中任意深度时的垂直土压力,也可得到每一个微元体对与之接触的HQ管壁段的摩擦力.
(4)既有顶管拱顶(GIH段)土压力计算.
GIH段对BC段产生向上的挟制力,因此该微元体除受到上下微元体传递的应力以及自身重力外,还受到支挡线外侧BC段土体受到的挟制力的反作用力,该反作用力可由BC段微元体平衡方程(7)得出.对GIH段取微元体进行分析,如图6 所示.
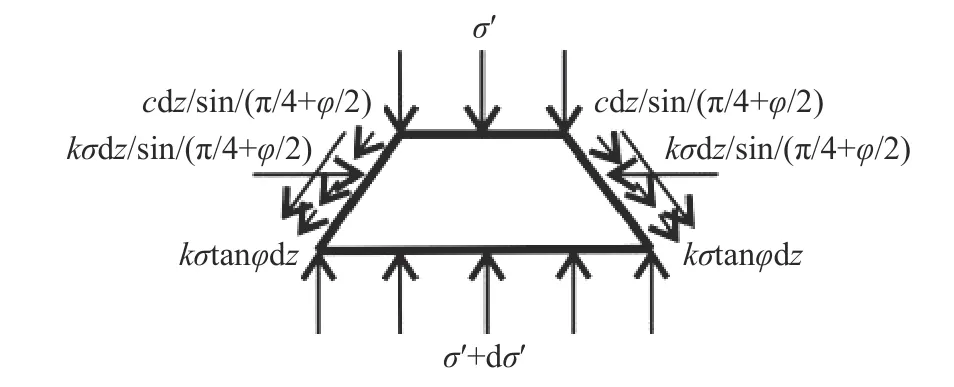
图6 GIH 段微元体受力示意图Fig.6 Schematic of force on the micro-element in the GIH segment
GIH段微元体上底的长度为:
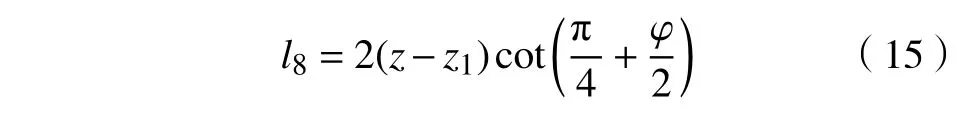
下底的长度为:
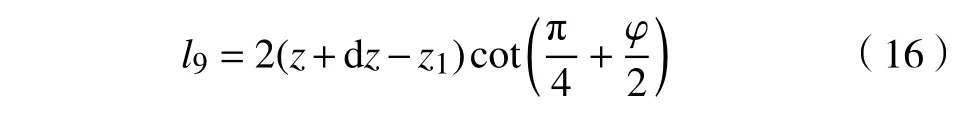
对微元体列竖向平衡方程得到:

其中,σ′为GIH段微元垂直土压力,kPa.该方程的初始条件为G点土压力为0,即z=z1时,σ′=0.把初始条件代入方程,即可得到既有顶管拱顶的垂直土压力.
(5)新建顶管拱顶土压力计算.
既有顶管除拱顶受到土压力之外,其IP、HQ段与向下位移的土体接触,还受到土体向下的摩阻力,如图7 所示.HQ段摩阻力可由方程(14)得出,IP段摩阻力与HQ段摩阻力相等.
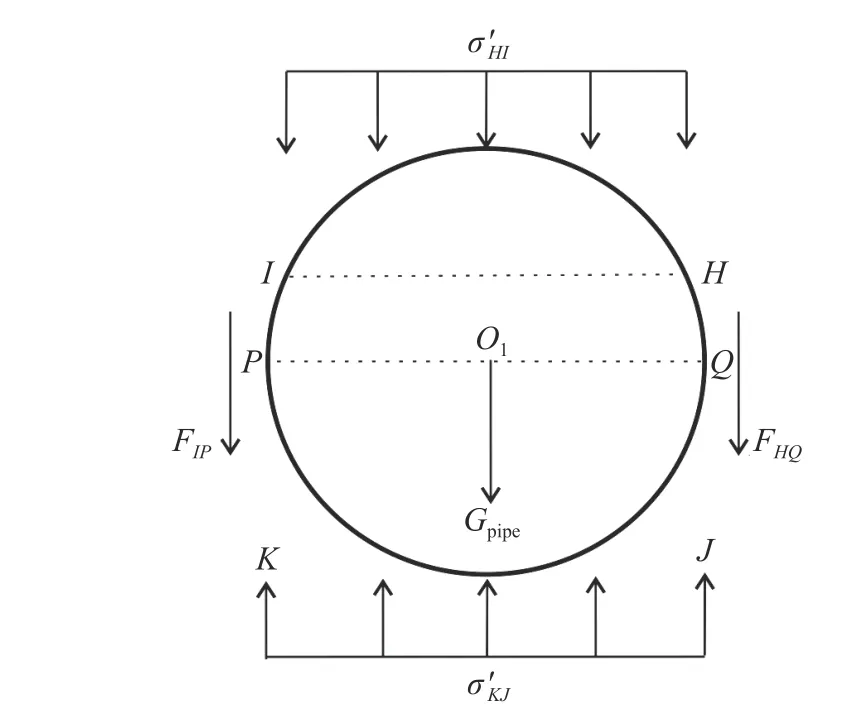
图7 既有顶管受力平衡示意图Fig.7 Schematic of force balance of the existing pipe jacking
根据既有顶管平衡条件,可知其受到底部土体的反力等于拱顶土压力、与土体接触段摩阻力及既有顶管自重之和,由此可得方程(18).根据假设条件(1),忽略了顶管外侧松动土体传递到新建顶管拱顶的应力后,既有顶管底部土反力与两管之间土体重力之和即为新建顶管拱顶的土压力,由此可得方程(19).由方程(18)及(19),可计算得到既有顶管土反力及新建顶管拱顶土压力:
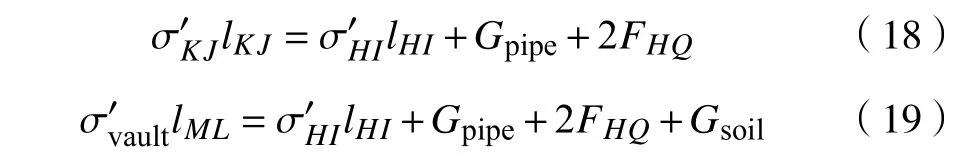
3 计算参数影响分析
根据本文构建的计算方法,编制Matlab 计算程序计算数值解,计算思路如下:把每一计算段分为若干个微元段,基于初始条件得出第一个微元段的竖向应力,把第一个微元段的结果作为第二个微元段中的初始条件,得出第二个微元段的竖向应力,依次得出所有微元段的竖向应力,进行加和,即可得到总的竖向应力.使用数值解法,同时能得出各微元段侧面摩擦力,加和得到该计算段总的摩擦力.分别取不同土体抗剪强度参数、顶管埋深以及顶管间距,计算下部新建顶管拱顶土压力,并与不考虑上部既有顶管支挡效应的土柱理论以及太沙基理论计算出的土压力(即下部管道单管顶进的土柱压力和太沙基土压力)进行对比分析.
3.1 土体力学参数影响分析
计算简图如图1 所示,顶进管道为两个大口径的薄壁钢管,考虑内摩擦角变化对新建顶管拱顶土压力的影响.计算中保持不变的参数有:两管管径均为2 m,壁厚为18 mm,既有顶管中心埋深为2.4 m,新建顶管中心埋深为4.8 m,土体黏聚力为10 kPa,重度为19 kN·m−3,侧压力系数k取值为1.土体内摩擦角为变化参数,计算中分别取:10°、15°、20°、25°和30°,相应地,每次计算中钢管管壁与土体的摩擦角取值为土体内摩擦角的1/3.计算内摩擦角变化对新建顶管拱顶土压力的影响,计算结果如图8 所示.
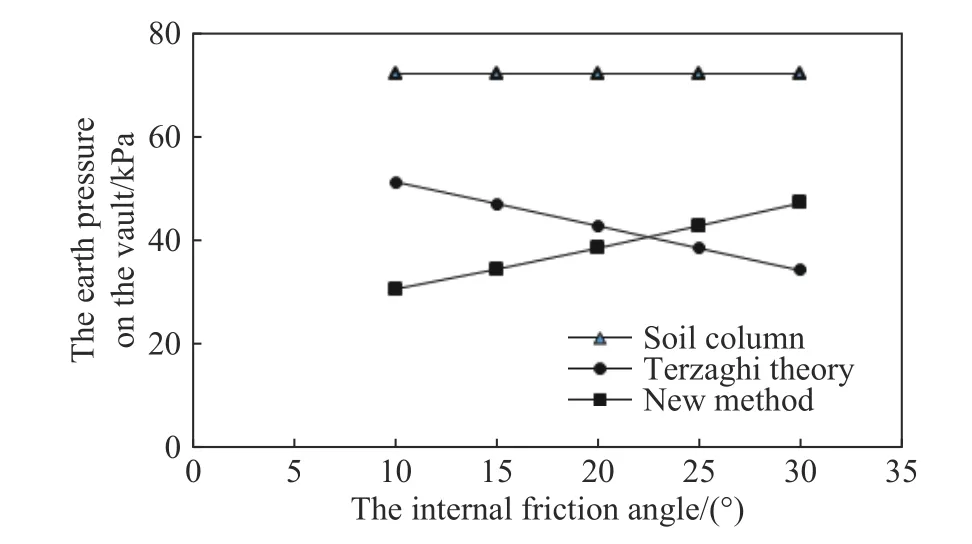
图8 内摩擦角影响分析Fig.8 Analysis of the internal friction angle impact
其余条件同上,土体内摩擦角为10°,钢管管壁与土体的摩擦角取值为土体内摩擦角的1/3(即3.33°),保持不变;而土体黏聚力取值分别为10、15、20、25 和30 kPa 时,考虑黏聚力变化对新建顶管拱顶土压力的影响,计算结果如图9 所示.
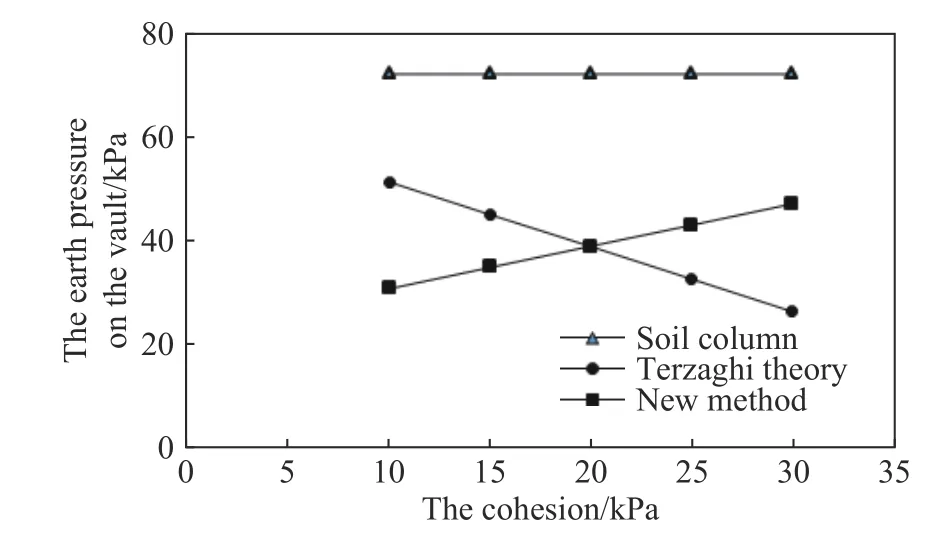
图9 黏聚力影响分析Fig.9 Analysis of the cohesion impact
由图8 和图9 可以得出如下结论:
(1)本文方法计算出的新建顶管拱顶土压力与土体抗剪强度相关,土体内摩擦角和黏聚力越大,计算土压力反而越小.分析其主要原因,新建顶管的拱顶压力与既有顶管拱顶土压力直接相关,而既有顶管拱顶土压力由其上部支挡的稳定土体提供.这部分稳定土体提供的黏聚力和摩擦力,会对周围向下位移土体造成向上的挟制效应,使得下移土体向下的压力降低,而稳定土体自身受到的反作用力,使其对既有顶管拱顶的压力增加.因此,土体抗剪强度越高,对松动土体的挟制力越大,导致既有顶管拱顶的土压力越大,而周围向下位移部分土体的土压力越小.对于新建顶管而言,考虑既有顶管的影响,当土体抗剪强度增加时,新建顶管拱顶土压力增加,而两侧的土压力会降低.
(2)当土体内摩擦角和黏聚力较小时,本文方法计算出的新建顶管拱顶土压力小于不考虑既有顶管支挡效应的太沙基理论计算出的土压力;当土体内摩擦角和黏聚力较大时,本文方法计算出的新建顶管拱顶土压力大于不考虑既有顶管的太沙基理论计算出的拱顶土压力.需要注意的是,拱顶计算的土压力值较大时,两侧松动土体土压力较小,因此并不代表新建顶管总体土压力值增加.
3.2 顶管埋深及管间距影响分析
计算简图如图1 所示,顶进管道为两个大口径的薄壁钢管,考虑顶管埋深变化对新建顶管拱顶土压力的影响.计算中保持不变的参数有:两管管径为2 m,壁厚为18 mm,土体黏聚力为10 kPa,土体内摩擦角为20°(钢管管壁与土体的摩擦角取值为土体内摩擦角的1/3,即6.67°),重度为19 kN·m−3,侧压力系数k取值为1.顶管埋深为变化参数,计算中分别取新建顶管管中心的埋深为:4.2、4.4、4.6、4.8 和5 m(相应地既有顶管管中心的埋深为:1.8、2.0、2.2、2.4 和2.6 m).计算顶管埋深对新建顶管拱顶土压力的影响,计算结果如图10 所示.
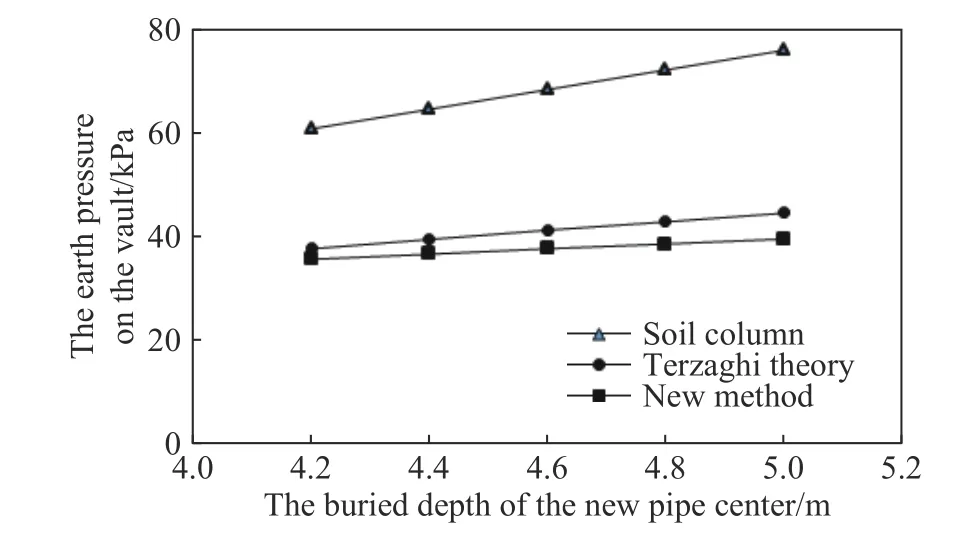
图10 顶管埋深影响分析Fig.10 Analysis of the buried depth impact
其余条件同上,当下部新建顶管埋深为4.8 m时,考虑两管不同间距(既有顶管的埋深随之变化)对新建顶管拱顶土压力的影响.计算中分别取管间距为:0.2、0.4、0.6、0.8 和1.0 m(相应地既有顶管管中心的埋深为:2.6、2.4、2.2、2.0 和1.8 m),计算结果如图11 所示.
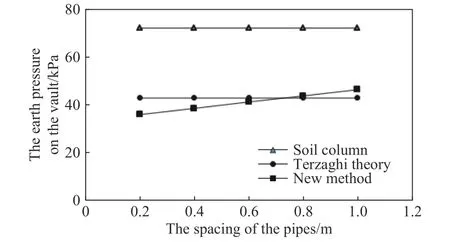
图11 顶管间距影响分析Fig.11 Analysis of the pipe jacking spacing impact
由图10 及图11 可以看出:
(1)当新建顶管埋深增加时,三种方法计算土压力均会增加,但本文构建的方法计算的新建顶管拱顶土压力增量最小.原因如下:土柱理论认为土体的自重造成了垂直土压力,埋深每增加1 m,土柱理论计算的土压力增量为土体重度;太沙基理论计算的土压力增量为土体向下重力增量与周围稳定土体的剪切阻力增量之差,显然小于土柱理论计算增量;而本文计算方法中,新建顶管的拱顶土压力增量等于既有顶管拱顶土压力增量,既有顶管拱顶土压力为拱顶稳定土体重力与周围下移土体提供的向下的挟制力之和,埋深增加,拱顶稳定土体体积不变,重力也不变,仅下移土体提供的向下的挟制力增加,其增量有限,故本文方法计算的土压力增量最小.
(2)随着两管管间距增加,本方法计算出的新建顶管拱顶土压力越来越大.新建顶管埋深不变,管间距增加时,既有顶管埋深减小,既有顶管拱顶土压力减小,而管间距的增加导致管间土体的重力增加.既有顶管拱顶土压力的减小量不及管间土体重力增加量,因此导致了新建顶管拱顶土压力的增加.
4 该方法存在的不足及拓展应用
4.1 该方法存在的不足
目前,小间距平行顶管的现场监测项目,主要涉及地表沉降和顶管顶力监测等.虽然管道土压力与顶力相关,但并不能从顶力监测结果反推出准确的土压力值.因为顶管壁后土压力监测的复杂性,导致小间距顶管土压力现场监测结果较少.在后续研究中,仍应多收集小间距平行顶管土压力现场监测结果,进一步对本文构建的计算方法进行验证.
本文方法中假设了太沙基松动线及既有顶管支挡线.关于太沙基松动线,本身就有诸多文献对其提出了改进意见[15−17].而本文所提出的问题还涉及到上部既有顶管的影响,情况较之单独的顶管工程更复杂,土体松动线直接使用太沙基松动线来进行假设,可能满足了部分情况下的计算结果(如第1 节中数值模拟情况),但是否满足不同的土体参数、埋深、管径和管间距等情况,还需进一步验证.其次,既有顶管支挡线,主要是基于数值模拟反分析以及极限平衡理论作出,也需要进一步验证.
总之,如能结合现场监测结果进一步考虑多方面的影响,对于土体松动线和既有顶管支挡线分类提出更为详细、合理的假设,即可保证该土压力计算方法在各种情况下的适宜性.
4.2 该方法的拓展应用
该方法相应的假设条件可根据不同的小间距平行顶管空间排列方式进行改进.在土体松动线和既有顶管支挡线等假设条件适宜的条件下,该方法可拓展应用于上下顶管管径不一致、两管非上下排列(中心线连线非垂直线)和小间距多线平行顶管等情况中.如图12 所示,为两管非上下排布时的情况,若左右两侧能给出合适的土体松动线及既有顶管支挡线假设条件,仍可用本文提出的方法计算新建管拱顶土压力.
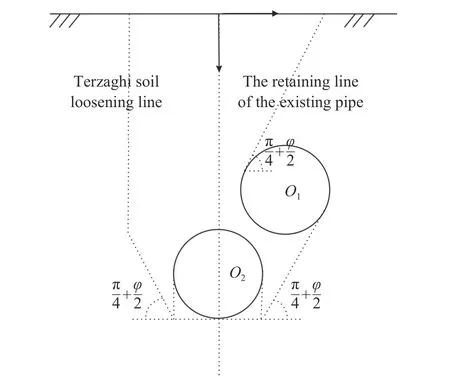
图12 两管不同排布情况下假设条件示意图Fig.12 Schematic of the assumed conditions in the different arrangement of the two pipes
5 结论
(1)为构建理论计算方法,提出了两个假设条件:既有顶管上方部分土体保持稳定;新建顶管拱顶应力为既有顶管底部的应力与两管间所夹土体的重力之和,两侧松动土体传递到新建顶管拱顶的力可忽略不计.通过数值模拟竖向位移及正应力云图验证了假设条件的合理性.在假设条件成立的基础上,基于太沙基理论和极限平衡理论,假定了新建顶管施工的土体松动线和既有顶管支挡线,进一步构建了上下排布的小间距平行顶管中,下部新建顶管拱顶的土压力计算方法.采用本文构建的理论方法计算出的数值模拟案例中新建顶管拱顶土压力稍大于数值模拟结果,也进一步验证了本文所构建计算方法的合理性.
(2)土体抗剪强度越大,新建顶管拱顶垂直土压力越大,而其侧面的土压力越小;抗剪强度较大时,本文方法计算结果小于太沙基理论计算结果,抗剪强度较小时,本文方法计算结果大于太沙基理论计算结果;顶管埋深增加时,新建顶管拱顶土压力增加,相较于土柱理论和太沙基理论,本文计算方法得出的新建顶管拱顶土压力增量最小;随着管间距增加,新建顶管拱顶土压力越来越大.
(3)本文构建的计算方法仍需大量的现场实测结果进行验证.该方法中假定的土体松动线及既有顶管支挡线,仍需要进一步考虑土体物理力学性质、管径、埋深、管间距等多方面的影响,进行更为详细、合理的分类假设,以保证该方法在各种情况下的适宜性.该方法中土体松动线及既有顶管支挡线经改进后,可拓展应用于各种不同空间排布方式的小间距两管、甚至多管顶进工程土压力计算.
