基于分形理论无腹筋混凝土梁的受剪性能

于 江，吕旭滨，秦拥军

新疆大学建筑工程学院，乌鲁木齐 830047

混凝土是由粗、细骨料、水泥水化物、未水化水泥颗粒、孔隙及裂缝等组成的非均匀多相材料且由于其成型工艺养护条件等原因，在混凝土搅拌成型前，在其内部已经具有了大量的毛细孔及微裂纹等初始缺陷[1]，这些初始裂纹缺陷经过萌生，发展，成核几个阶段最终形成宏观的裂纹并导致混凝土构件发生破坏[2].其裂纹发展往往呈现出“Z”字状并在宏观裂纹四周延伸出众多纵横交错的微小裂纹，这种具有随机性的裂纹分布使得构件破断裂面呈现出凹凸不平的形态.分形理论被看作为分析处理材料中的不规则现象的一种新型手段，现被广泛应用在混凝土等众多具有大量非线性分布的微观、宏观裂纹缺陷的多相复合材料.对于无腹筋混凝土梁的受剪破坏研究一般采用经典损伤力学、断裂力学等理论进行研究，但利用传统的力学分析手段很难对这些混凝土裂缝损伤缺陷进行精确的判断，只是局限于某一层面上的解释，在实际工程应用中表现较好，但在理论上还是会有或多或少的不足[3]，因此我们尝试采用可以定量分析描述斜裂纹发展分布等特征的分形理论对混凝土的裂缝损伤进行分析.本文通过9 根无腹筋混凝土梁试验，应用分形理论得出了在不同剪跨比作用下无腹筋混凝土梁斜裂缝的分布规律，证明了分形理论是分析无腹筋梁表面裂缝中一种十分有效的方法.

1 分形理论

分形理论于1975 年被Mandelbrot 与Wheeler[4]定义，被用作分析描述具有“不规则、不平整”等特性的物体.分形维数D是描述结构分形现象特征过程中的一个量化定义[5]，分形理论要求结构应具有自相似性即结构中的任何一部分应与结构整体具有相似的特征现象.混凝土作为一种集成材料，根据研究表明其骨料集配、微观孔结构、表面裂缝都具有分形效应[6-10].董毓利等[11]对于混凝土声发射b值及分形维数建立联系，吴科如教授及其研究团队[12-13]通过激光法测定了混凝土断裂面的分形维数D，徐志斌与谢和平[14]借助分形理论与损伤力学描述了分形维数D与损伤变量k之间的联系.Carpinteri 等利用分形理论对混凝土与岩石的尺寸效应进行了深入的研究[15-16]，秦子鹏等[17]探究BFRP 布加固钢筋混凝土梁抗弯性能的分形效应，周瑞忠[18]分析了混凝土裂纹宽度的分形现象，验证了裂纹宽度亦具有尺寸效应.

上述研究成果表明，分形理论可以利用混凝土的表面裂缝定性地描述混凝土受载过程中的剪切性能，本文通过不同剪跨比及纵筋配筋率作用下的无腹筋混凝土梁的试验加载结果，分析了无腹筋混凝土梁在剪切破坏下梁表面的裂缝发展趋势及分布形式，验证了梁在受载过程中不同剪跨比作用下的无腹筋混凝土梁表面裂缝的分布具有分形特征，并获得其在加载全过程中每级荷载所对应的分形维数D；研究了全梁区域的表面裂缝分形维数与荷载、极限承载力、跨中挠度及延性系数之间的关系.分析的结论可以为无腹筋混凝土梁剪切性能方面的研究及实际工程中分形理论的运用提供理论依据.

2 试验概况

2.1 试验原材料与配合比

本次试验采用红雁牌P·O 42.5 普通硅酸盐水泥，其化学性能如表1，粗骨料采用新疆乌鲁木齐市乌拉泊采石场连续级配为5～25 mm 的天然卵石，其物理性能如表2，细骨料选用乌鲁木齐地区的中砂，细度模数为2.9，表观密度为2640 kg·m-3，拌合水采用乌鲁木齐当地自来水.

表1 水泥的化学成分(质量分数)Table 1 Chemical composition of cement %

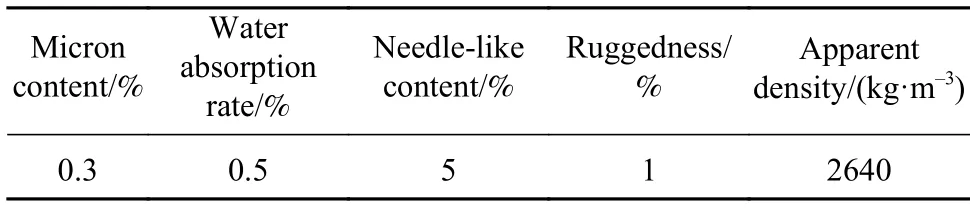
表2 粗骨料的实验性能Table 2 Properties of coarse aggregate

2.2 试验方案

试件采用矩形截面简支梁，梁长1800 mm，净跨为1400 mm，矩形截面尺寸是150 mm×250 mm，梁底设立2 根纵筋，梁的腹部不设架立筋及箍筋，在支座外设立3 根直径为6 mm 的HPB300 的箍筋，间距为60 mm，保护层厚度为20 mm，图1 为梁的尺寸及配筋图.

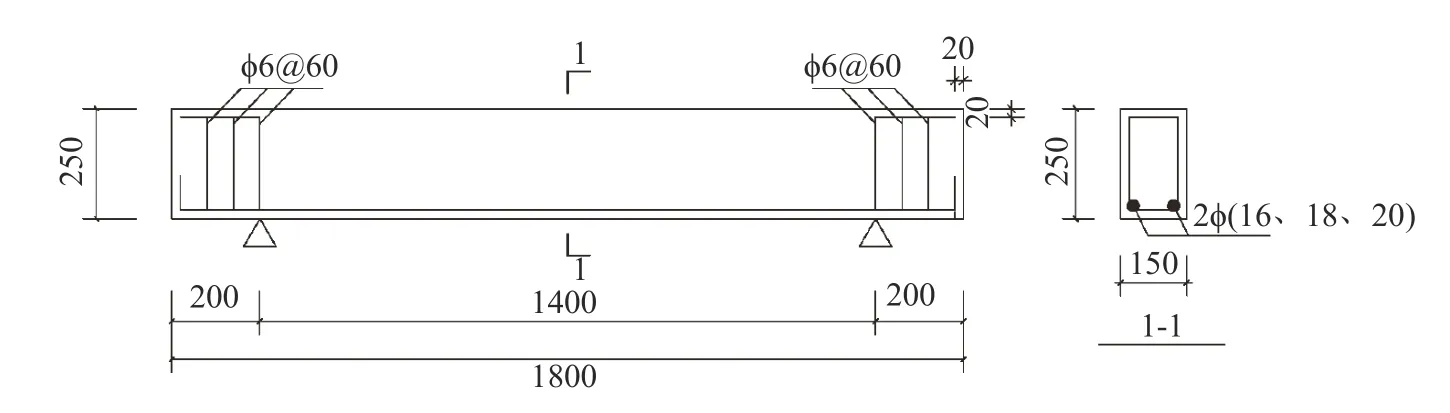
图1 无腹筋梁尺寸及配筋图（单位:mm）Fig.1 Dimensions and reinforcement drawing of girder without rib (Unit:mm)

为了研究不同剪跨比λ及纵筋配筋率作用下无腹筋梁表面裂缝的分形特征与抗剪性能间的联系，本次试验设计采用9 根试验梁，共分成3 组，而剪跨比对无腹筋梁受剪破坏影响程度最大，由于不配置腹筋，在此不考虑腹筋率作用，纵筋配筋率影响次之，为了贴近实际工程应用，设定梁发生剪压破坏（1<λ>3）与适筋破坏，对比斜拉与斜压破坏，剪压破坏延性较大，脆性较低，为了确保试件的延性相对更大；挑选纵筋配筋率作为一个主要因素，是为了一方面得到其对无腹筋梁受剪性能的影响，另一方面通过分形维数得到其对裂纹扩展的影响程度.因此选取下述剪跨比及纵筋配筋率.因此第一组梁的纵筋配筋率为1.28%，第二组为1.62%，第三组为1.99%，且每组设定剪跨比依次为1.5、2、2.5，并分别测试与每组梁同条件养护条件下的混凝土立方体试块抗压强度，试验参数见表3.

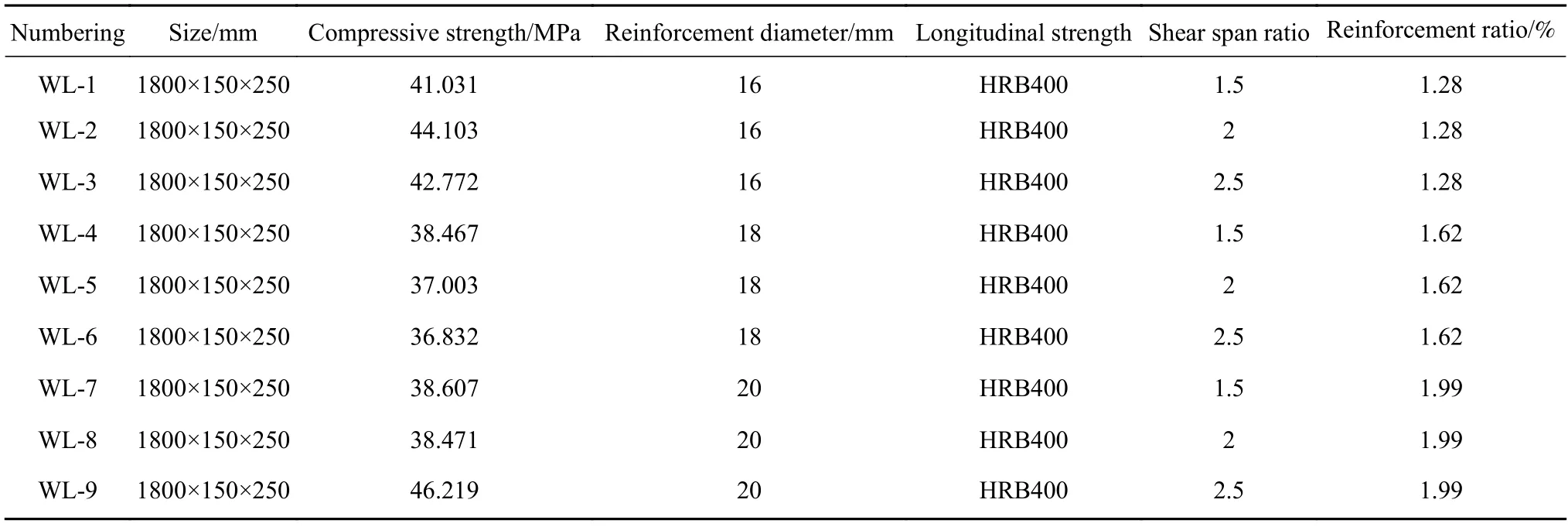
表3 试件参数信息Table 3 Parameter information of test pieces

2.3 试验加载方案

按照GB 50152—2012《混凝土结构试验方法标准》对无腹筋混凝土梁进行四点加载，并在梁顶端放置一个分配梁将力分导为2 个对称的集中荷载，试验加载装置采用液压千斤顶，由于试验条件有限，未采用位移加载选用力加载方式，且为了方便控制加卸载速度和观测分析结构的各种变化，也为了统一各点的加载步调采用分级加载的方式，加载后持续3 min 用以记录梁的裂缝等，在梁出现裂缝前采用每级5 kN 加载，出现裂缝后以10 kN 加载，当加载到试验梁破坏荷载的90%时，改为每级5 kN 加载，直至梁发生破坏，试验加载装置及位移计布置图如图2 所示.

图2 加载装置布置图.（a）λ=1.5；（b）λ=2；（c）λ=2.5；（d）现场布置图Fig.2 Load device layout:(a) λ=1.5;(b) λ=2;(c) λ=2.5;(d) site layout

试验加载过程中详细记录裂缝的发展趋势与相应的荷载值，并使用DH3816 采集箱采集应变（纵筋、跨中混凝土、应变片花）、跨中与支座处的位移及荷载值等数据.

3 试验结果分析

3.1 梁表面裂缝分布

基于试验过程的观察，当9 根无腹筋梁受到荷载作用时，在到达开裂荷载之前，并无任何现象产生，当加载到极限荷载的20%～25%时，在梁的跨中底部会率先出现数条微小的垂直裂缝，随后在无腹筋梁的弯剪区的受拉区边缘产生一些垂直裂缝，这些垂直裂缝沿垂直方向发展一小段距离后将会沿斜向发展，并且发展的较为迅速进而演变成一条沿梁高贯穿的临界斜裂缝，其总体发展走向是沿支座到加载点部位，而此时跨中的裂缝也已停止发展且最终停留在梁的2/3 高度，而临界斜裂缝的出现也将导致了剪弯段剪压区高度减小，随着荷载的增加，裂缝宽度也逐渐增大，加载点部位混凝土被压碎，最终梁发生破坏，试验梁加载停止.图3 为各组无腹筋梁受载过程中裂缝演化分布图，其中粗线为最终主导破坏的裂纹.

图3 试验梁裂缝分布图.（a）WL-1；（b）WL-2；（c）WL-3；（d）WL-4；（e）WL-5；（f）WL-6；（g）WL-7；（h）WL-8；（i）WL-9Fig.3 Crack distribution of test beam:(a) WL-1;(b) WL-2;(c) WL-3;(d) WL-4;(e) WL-5;(f) WL-6;(g) WL-7;(h) WL-8;(i) WL-9

3.2 荷载-挠度曲线

根据试验全过程中所采集的荷载及跨中挠度，并绘制荷载-挠度曲线，如图4 和图5 所示.

基于图4 的曲线分布情况，在不同纵筋配筋率ρ的加载作用下，λ=1.5 时，三种不同纵筋配筋率的无腹筋梁，每级荷载作用下的跨中挠度值差异值较小，基本处于一条直线，随着剪跨比λ的增大，在不同纵筋配筋率的作用下，每级荷载所对应的挠度值差异性越大，总体趋势表现为纵筋配筋率为1.28%的梁在每级荷载下的挠度值最大，而纵筋配筋率为1.62%的梁每级荷载所对应的跨中挠度最小.纵筋配筋率为1.99%的梁跨中挠度次之.这表明纵筋配筋率为1.62%的无腹筋梁延性相对较好，纵筋配筋率越小，梁抵抗变形能力越弱，而纵筋配筋率偏大对于无腹筋梁的挠度控制会起反作用，因此适当的控制纵筋配筋率可以有效的控制梁的挠度.

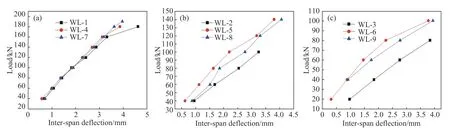
图4 相同剪跨比、不同纵筋配筋率作用下的荷载与挠度间关系.（a）λ=1.5；（b）λ=2；（c）λ=2.5Fig.4 Relationship between load and deflection under the same shear-span ratio and different longitudinal reinforcement ratios:(a) λ=1.5;(b) λ=2;(c) λ=2.5

在不同剪跨比作用下，根据图5 的描述，在同一纵筋配筋率条件下，剪跨比越大，在同级荷载作用下的跨中挠度值越大，剪跨比与无腹筋梁的挠度呈现正相关关系.而伴随着纵筋配筋率的增大，这种规律性亦表现的较为明显.

图5 相同纵筋配筋率、不同剪跨比作用下荷载与挠度间的关系.（a）ρ=1.28%；（b）ρ=1.62%；（c）ρ=1.99%Fig.5 Relationship between load and deflection under the same longitudinal reinforcement ratio and different shear span ratios:(a) ρ=1.28%;(b) ρ=1.62%;(c) ρ=1.99%

3.3 开裂荷载与极限荷载

WL-1、WL-2 和WL-3 梁在加载过程中，可以发现伴随着剪跨比λ的增大，其开裂荷载依次减小，在跨中率先产生竖向裂缝，随后在剪弯区出现竖向裂纹并逐渐发展为临界斜裂缝，最终无腹筋梁产生破坏，都属于剪压破坏，其相应的极限荷载随着试验梁设定的剪跨比λ的增大而逐渐减小.WL-4、WL-5、WL-6、WL-7、WL-8 和WL-9 发展趋势与上述相同，都属于剪压破坏.图6 是试验梁开裂荷载及极限荷载的对比图，当剪跨比相同时，各组梁的开裂荷载并无明显的区别，随着纵筋配筋率的增大，极限荷载也有较大的提高，且随着剪跨比的增大提高的程度也逐步增大.

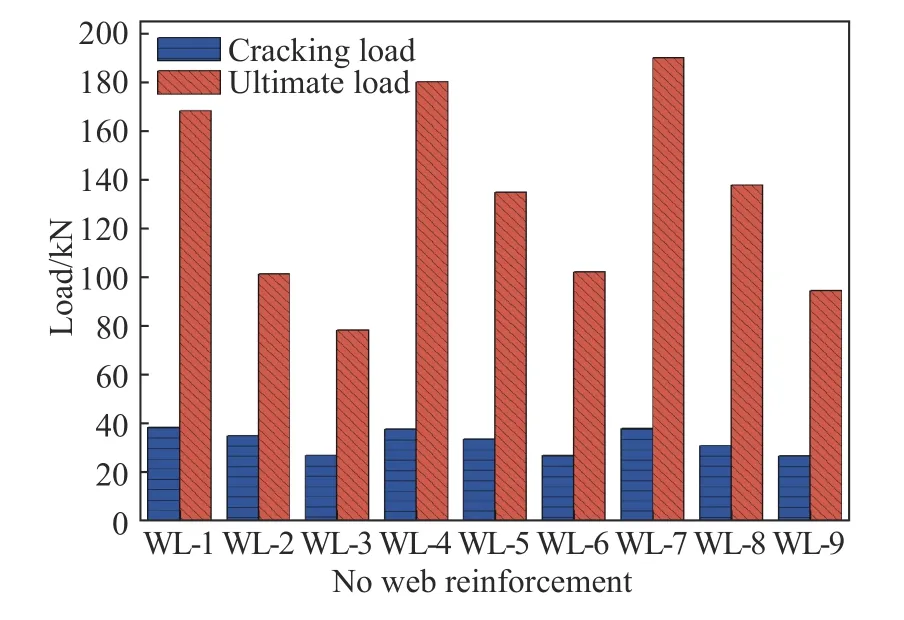
图6 开裂荷载与极限荷载对比图Fig.6 Comparison of cracking load and ultimate load

4 基于分形理论的试验结果分析

4.1 裂缝分形维数D 的理论计算

不规则的图像多种多样，并不是所有都具备分形特征，唯有在一定标度范围中满足自相似性的图像才被称为具有分形特征[19].无腹筋混凝土梁在加载过程中裂缝分布具有随机性，是否具有分形特征还有待验证，基于分形理论对图像的分形维数的计算方法有：盒维数法[20-21]、分形布朗运动模型法[22-23]、小岛法[24]和投影覆盖法[25-26]等.针对混凝土梁表面裂缝的分形维数的测量一般选用盒维数法.计算步骤为：采用规格为L×L的正方形网格去覆盖无腹筋混凝土全梁的裂缝分布区域，统计计算出覆盖区域内存在裂缝的网格数目并记为N(L)，随后利用改变网格边长L来改变网格密度并统计N(L)，绘制lnN(L)-ln(1/L)的图像.若关系曲线满足线性关系，则证明梁表面的裂缝具有自相似性[27]，拥有分形特征.lnN(L)-ln(1/L)关系曲线的斜率即为分形维数.分形维数D表示为

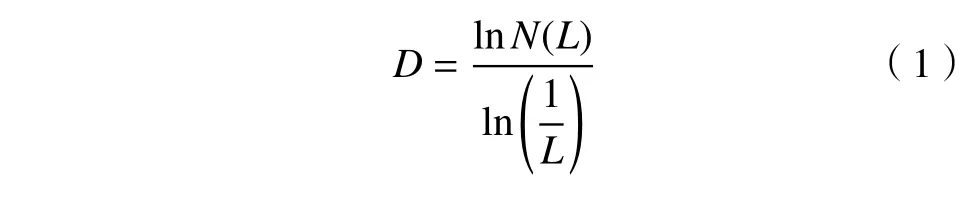
4.2 荷载作用梁表面裂纹的分形研究

基于试验梁在分级加载过程中对裂缝的定位及描绘，将每个试件的裂缝转换为数字图像，通过盒计数法计算在不同等级荷载作用下的分形维数，设定盒的尺寸为30～150 mm，共13 种尺寸，每种尺寸相隔10 mm，将这13 种尺寸的盒网格覆盖到无腹筋梁的表面，统计出存在裂缝的格子数N(L)，并绘制lnN(L)-ln(1/L)的图像如图7.

由图5 可以看出，基于不同剪跨比及纵筋配筋率的无腹筋梁，其加载全过程中的裂缝发展分布在不同网格尺寸覆盖下所展示的lnN(L)-ln(1/L)曲线具有明显的线性关系，这无腹筋梁表面的裂缝在一定标度范围内具有分形特征.通过图7 能明显的发现荷载等级越大，lnN(L)-ln(1/L)曲线的斜率越大，这代表其分形维数也越大.表4 为在不同荷载作用下无腹筋梁表面的分形维数.

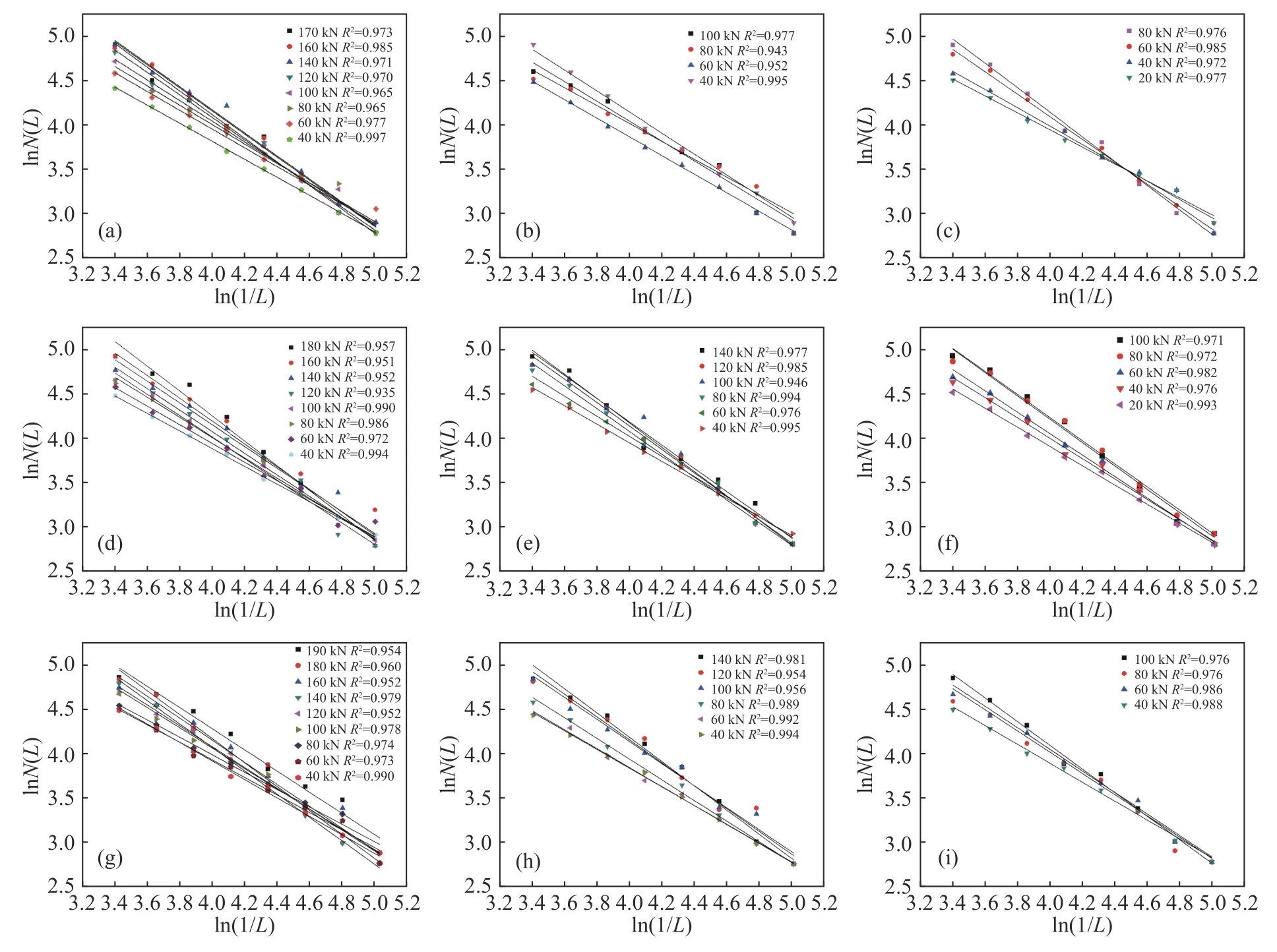
图7 不同等级荷载下梁表面的lnN(L)-ln(1/L)图.（a）WL-1；（b）WL-2；（c）WL-3；（d）WL-4；（e）WL-5；（f）WL-6；（g）WL-7；（h）WL-8；（i）WL-9Fig.7 lnN(L)-ln(1/L) diagram of beam surface under different grades of load:(a) WL-1;(b) WL-2;(c) WL-3;(d) WL-4;(e) WL-5;(f) WL-6;(g) WL-7;(h) WL-8;(i) WL-9

根据表4 所示，伴随着每级荷载的增加，分形维数亦在相应的增大.而分形维数可以较好地反映梁内部的损伤程度，分形维数与梁内部的损伤程度成正比关系，分形维数越大，无腹筋梁内部的损伤越大.9 组无腹筋梁中，最小和最大分形维数（Dmin和Dmax）分别为0.964 和1.449.

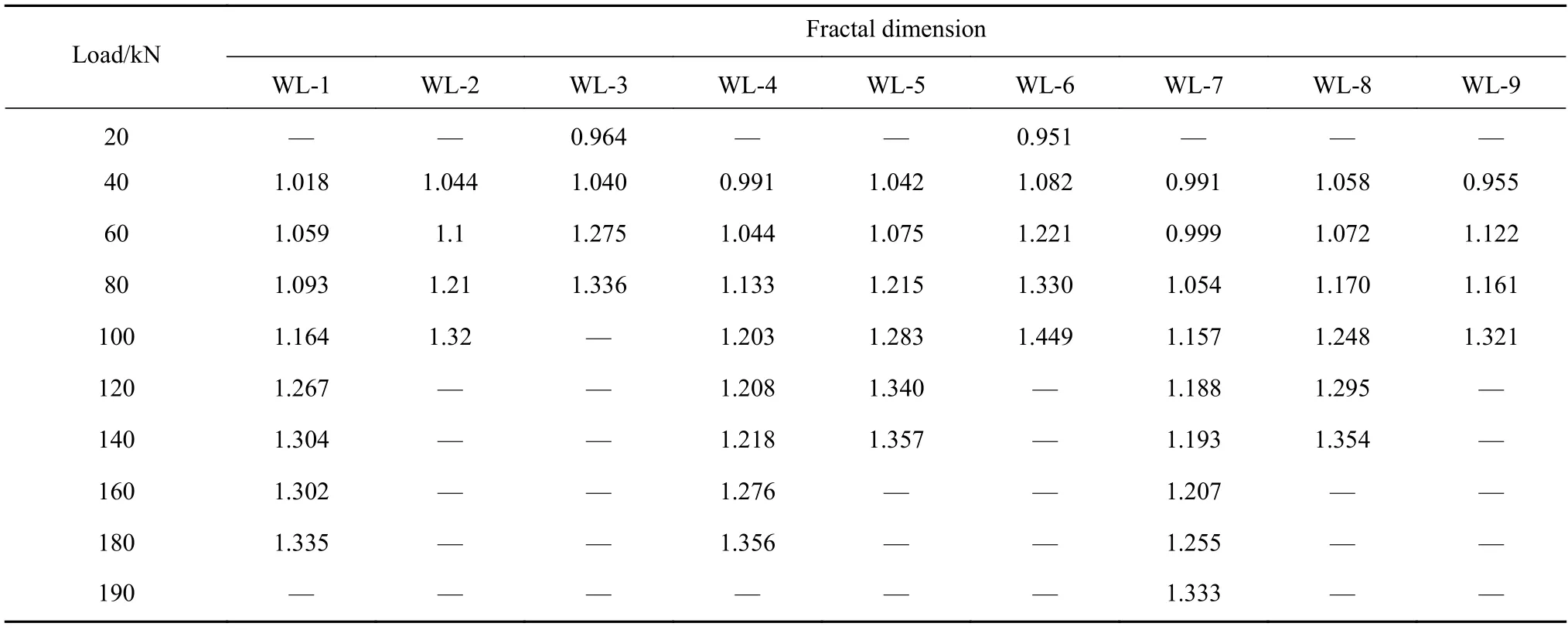
表4 不同荷载作用下梁表面分形维数Table 4 Fractal dimension of beam surface under different loads

4.3 极限荷载作用下梁表面的分形研究

针对无腹筋梁受载破坏时梁表面裂缝分布分形维数进行探究，可以较好的分析其在不同剪跨比及纵筋配筋率下的破坏形式.选取每组无腹筋梁基于极限荷载作用下的裂缝进行计算统计，绘制lnN(L)-ln(1/L)曲线，如图8 所示.

通过图8 可以发现各组梁的lnN(L)-ln(1/L)曲线都具有较好的线性关系，这表明：无腹筋梁在极限荷载作用下的梁表面裂缝仍然具有分形特征，不论在梁加载阶段还是破坏阶段都可以通过分形几何学进行分析.

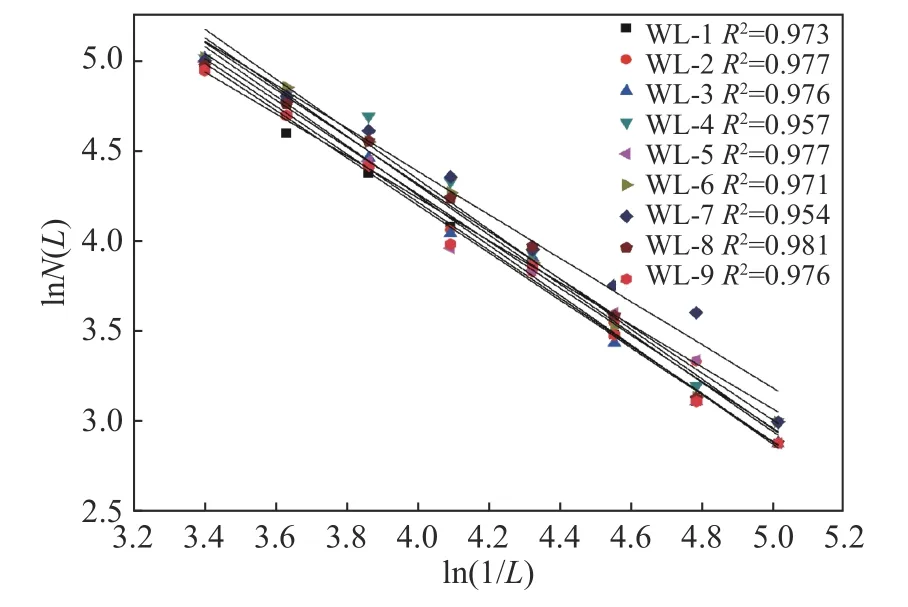
图8 极限荷载下梁表面的lnN(L)-ln(1/L)图Fig.8 lnN(L)-ln(1/L) diagram of the beam surface under ultimate load

图9 表示在极限荷载作用下各组无腹筋梁表面裂缝分形维数的对比图.通过对比图中各个试件的分形维数，可以发现在极限荷载作用下，各组无腹筋混凝土梁表面的分形维数变化幅度不大，稳定在一个固定的界面，其数值变化范围为1.321～1.449，普遍都在1.33 附近，这表明在不同剪跨比及纵筋配筋率的作用下，无腹筋梁最终破坏时表面裂缝的分形维数变化范围较小，剪跨比与纵筋配筋率对其影响较小.

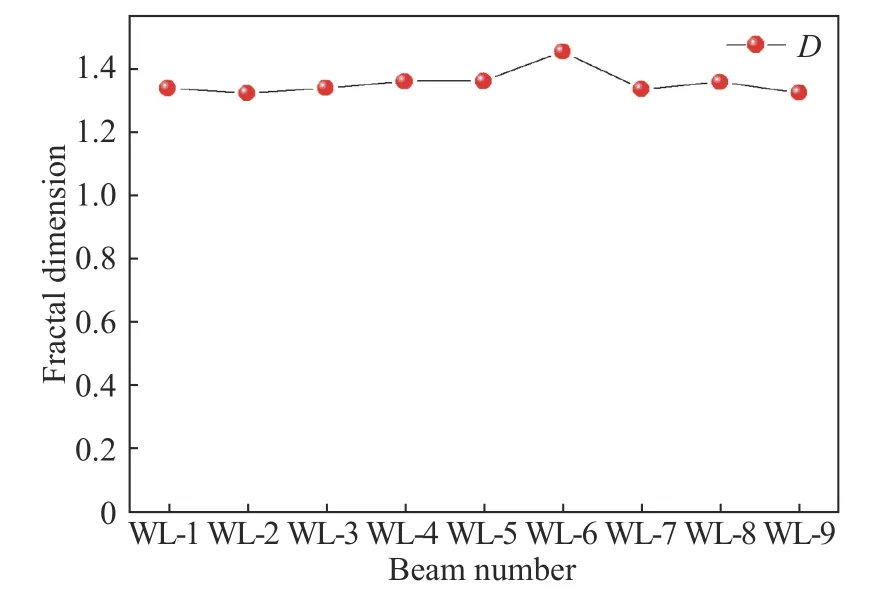
图9 极限荷载作用下梁的分形维数Fig.9 Fractal dimension of the beam under ultimate load

4.4 分形维数与极限承载力间的关系

统计各组无腹筋梁的极限荷载，并绘制基于不同剪跨比与纵筋配筋率的分形维数与极限荷载的曲线，如图10 和11 所示.

根据图10 和11 所示，可以发现分形维数与试验梁极限荷载之间的规律性较弱，在相同剪跨比不同纵筋配筋率的条件下，其无腹筋梁表面裂缝的分形维数表现为先增大后减小，而在相同配筋率不同剪跨比条件下，其分形维数与极限荷载表现的差异性较大，总体而言，在不同剪跨比及纵筋配筋率作用下，对于极限荷载作用下的裂缝扩展将产生不同的影响，裂缝的扩展及分布具有不同的形态，进而使分形维数也产生较大的差异性，规律性较小，在今后有待深入探究.

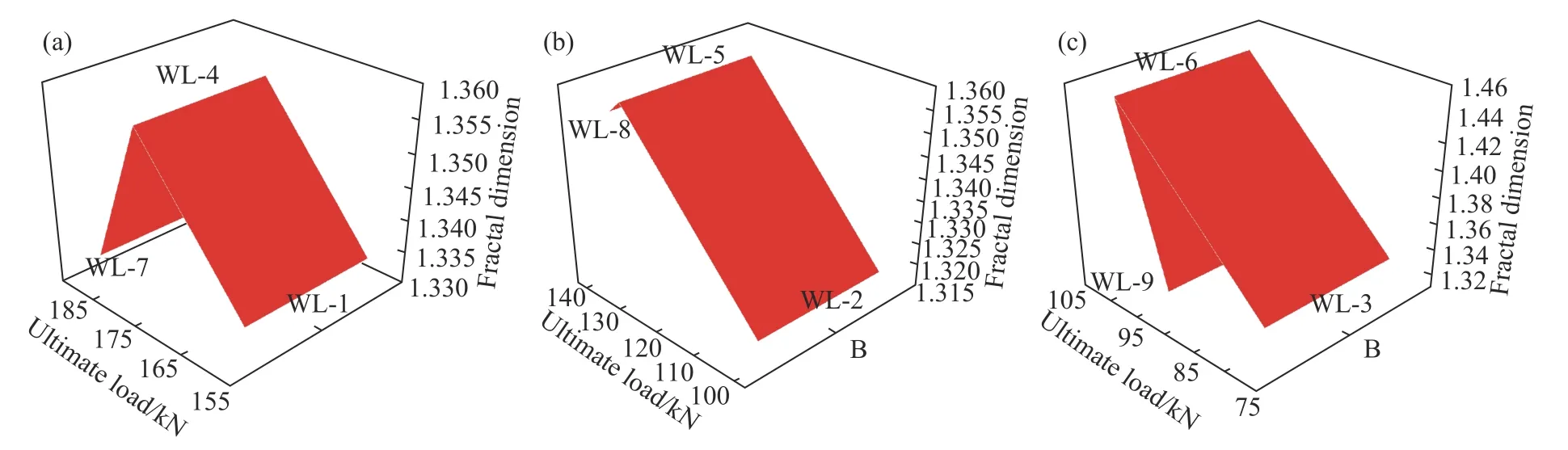
图10 相同剪跨比、不同纵筋配筋率作用下的极限荷载与分形维数间的关系.（a）λ=1.5；（b）λ=2；（c）λ=2.5Fig.10 Relationship between ultimate load and fractal dimension under the same shear span ratio and different longitudinal reinforcement ratios:(a) λ=1.5,(b) λ=2,(c) λ=2.5

4.5 分形维数与分级荷载间的关系

基于无腹筋混凝土梁不论在分级荷载作用下还是极限荷载作用下都具有分形特征，通过表4，建立分形维数D与分级荷载F之间的联系.

如图12 和图13 所示，基于两种不同变量作用下的荷载-分形维数的曲线呈现较好的对数关系，其拟合的数学方程如式2，k和m为参数，数值如表5所示.λ为试验梁剪跨比，ρ为纵筋配筋率.

表5 分级荷载与分形维数关系的k、m 值Table 5 k,m values of the relationship between the graded load and the fractal dimension

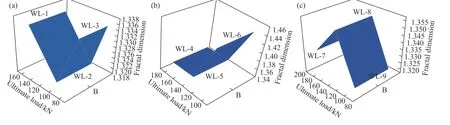
图11 相同纵筋配筋率、不同剪跨比作用下的极限荷载与分形维数间的关系.（a）ρ=1.28%；（b）ρ=1.62%；（c）ρ=1.99%Fig.11 Relationship between ultimate load and fractal dimension under the same longitudinal reinforcement ratio and different shear span ratios:(a) ρ=1.28%;(b) ρ=1.62%;(c) ρ=1.99%

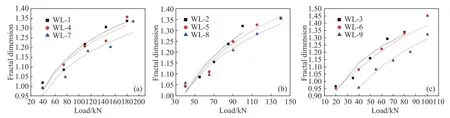
图12 相同剪跨比、不同纵筋配筋率作用下的分级荷载与分形维数间关系.（a）λ=1.5；（b）λ=2；（c）λ=2.5Fig.12 Relationship between the graded load and the fractal dimension under the same shear span ratio and different longitudinal reinforcement ratios:(a) λ=1.5;(b) λ=2;(c) λ=2.5

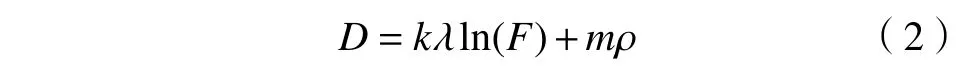
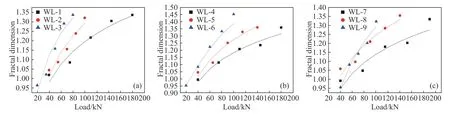
图13 相同纵筋配筋率、不同剪跨比作用下的分级荷载与分形维数间关系.（a）ρ=1.28%；（b）ρ=1.62%；（c）ρ=1.99%Fig.13 Relationship between the graded load and the fractal dimension under the same longitudinal reinforcement ratio and different shear span ratios:(a) ρ=1.28%;(b) ρ=1.62%;(c) ρ=1.99%

当荷载按照规范依次增加，分形维数也不断增加，且在不同荷载等级下，不同剪跨比及纵筋配筋率作用下，荷载-分形维数拟合曲线呈现出不同的分布形态.如图13 所示，在无腹筋混凝土梁表面裂缝的荷载-分形维数曲线的曲率随着剪跨比的增大逐渐减小.这是在没有腹筋作用情况下，由于剪跨比在一定程度反映截面弯矩与剪力的相对比值，它对无腹筋梁的斜截面受剪破坏具有决定性的影响，剪跨比越小，无腹筋梁的承载力越高，梁表面的裂纹发展越充分，其分形维数也越大.同样的在不同纵筋配筋率作用下，如图12 所示，随着纵筋配筋率的逐渐增大，荷载-分形维数曲线的曲率越大，在同一荷载作用下，纵筋配筋率越大，分形维数越小，裂纹相对较少，这是由于纵筋配筋率的增大，纵筋与混凝土黏结强度越高，其抗拉能力越高，在分级荷载作用下裂纹发展较为充分，在同等荷载等级下分形维数也相较更小.因此剪跨比与纵筋配筋率对于无腹筋混凝土梁的裂缝发展及承载力的变化都具有显著的影响.

4.6 分形维数与跨中挠度的关系

采集无腹筋混凝土梁加载全过程的跨中挠度，并拟合在不同变量作用下跨中挠度-分形维数的曲线如图14 和图15.

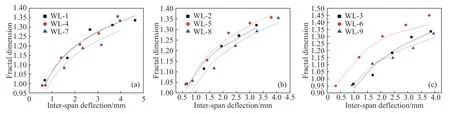
图14 相同剪跨比、不同纵筋配筋率作用下的跨中挠度与分形维数间的关系.（a）λ=1.5；（b）λ=2；（c）λ=2.5Fig.14 Relationship between mid-span deflection and fractal dimension under the same shear-span ratio and different longitudinal reinforcement ratios:(a) λ=1.5;(b) λ=2;(c) λ=2.5

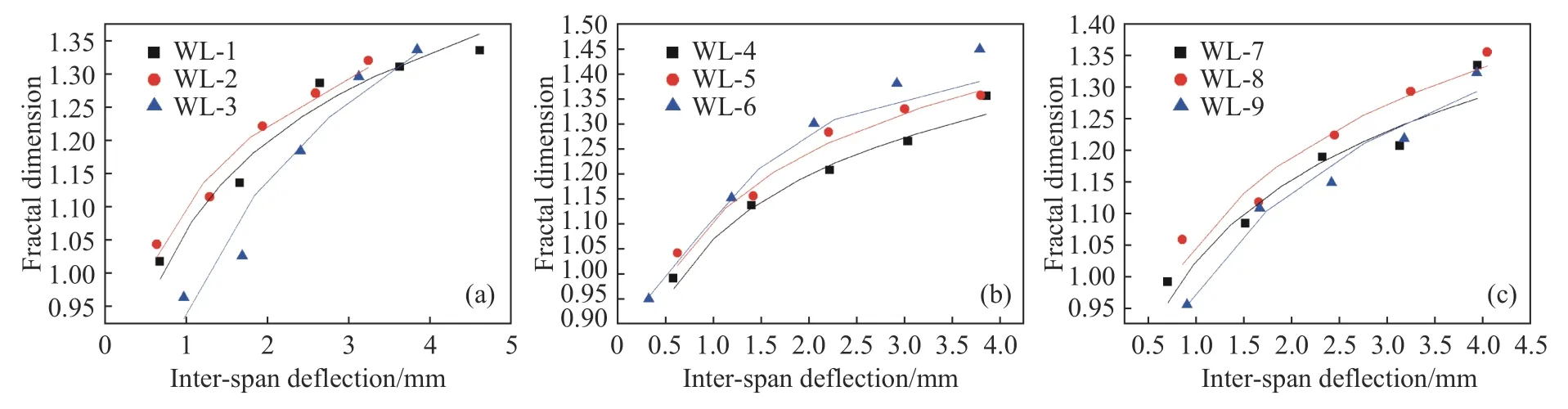
图15 相同纵筋配筋率、不同剪跨比作用下的跨中挠度与分形维数间关系.（a）ρ=1.28%；（b）ρ=1.62%；（c）ρ=1.99%Fig.15 Relationship between mid-span deflection and fractal dimension under the same longitudinal reinforcement ratio and different shear-span ratios:(a) ρ=1.28%;(b) ρ=1.62%;(c) ρ=1.99%

根据图14 所示，跨中挠度-分形维数曲线在不同剪跨比作用下表现出较好的对数关系，曲线曲率的差异性较为明显，跨中挠度-分形维数曲线的曲率随着纵筋配筋率的增大表现出先增大后减小的趋势，纵筋配筋率ρ=1.62%的无腹筋梁其荷载-分形维数曲线的曲率相对最高，而剪跨比作用下的其他曲线的差异性较大，其所表现的规律性较不明显，因此剪跨比对跨中挠度的变化影响程度相对较小，但基于图14 和图15 中能发现在不同剪跨比与纵筋配筋率的作用下，跨中挠度-分形维数曲线亦呈现较好的对数关系，分形维数D与跨中挠度y具有正比关系，其数学表达式如式（3）所示.

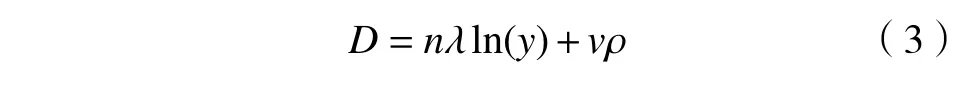
式中，n和v为参数，数值如表6 所示.

表6 跨中挠度与分形维数关系的n、v 值Table 6 n,v values of the relationship between the mid-span deflection and the fractal dimension

5 结论与展望

（1）无腹筋混凝土梁在不同剪跨比与纵筋配筋率作用下呈现出剪跨比与极限荷载及开裂荷载成反比，而纵筋配筋率与极限荷载成正比，但对开裂荷载的影响程度相对较小.

（2）无腹筋混凝土梁表面的裂缝分布不论在分级荷载作用还是极限荷载作用下都在一定标度范围内拥有分形特征，且在分级荷载作用下，分形维数在0.964～1.449，在极限荷载作用下的分形维数在1.33 附近.

（3）在不同剪跨比及纵筋配筋率作用下，分级荷载、跨中挠度与无腹筋混凝土梁表面裂缝的分形维数呈现较好的对数关系，分级荷载-分形维数曲线受剪跨比及纵筋配筋率的影响表现出一定的规律性，但极限荷载-分形维数之间线性关系不明显，伴随着纵筋配筋率的增大呈现出先增大后减小的趋势，随着剪跨比的增大呈现的差异性较大.而跨中挠度受剪跨比的影响较小，受纵筋配筋率的影响，跨中挠度-分形维数曲线的曲率呈现出先增大后减小的趋势.

（4）基于分形理论研究无腹筋混凝土梁表面裂缝时定量的对试件的剪切性能的描述，这一方法是可行、可靠的，且为今后对无腹筋混凝土梁剪切性能的研究提供一定的依据.

（5）考虑纵筋配筋率及剪跨比作用的无腹筋混凝土梁在分形理论的处理下，分形维数与梁的受力性能及微观特征之间的关系还需要大量的试验验证，有待进一步探究.