单晶铜塑性变形的二维离散位错动力学模拟研究

2021-10-23王春晖孙朝阳郭祥如魏云灿

工程科学学报 2021年10期

王春晖，孙朝阳，郭祥如，魏云灿，蔡旺

1) 北京科技大学机械工程学院,北京 100083 2) 北京科技大学金属轻量化成形制造北京市重点实验室,北京 100083 3) 北京科技大学顺德研究生院,佛山 528000 4) 天津理工大学天津市先进机电系统设计与智能控制重点实验室,天津 300384

随着以传感器和激励器为代表的微机械微电子元器件的广泛应用和发展，亚微米尺度晶体材料表现出明显区别于宏观尺度材料的力学行为[1−2]，如尺寸效应[3−5]、时空不连续性[6−7]以及应变率敏感性[8−9].为了评估并预测亚微米尺度晶体元器件在加工和服役中的性能，需要搭建起反常力学响应与微结构演化的桥梁，分析其在不同加载方式和应变率下的力学响应和位错机制.

实验研究表明，单向压缩的亚微米尺度单晶在不同加载方式下呈现显著的时空不连续性：在力加载时，应力−应变曲线呈现台阶状；在位移加载时，应力−应变曲线呈现锯齿状.离散位错则以类似“雪崩”的方式贡献塑性应变，在晶体表面形成很多滑移带和滑移线[10−11].Papanikolaou 等[12]和Maaß等[13]通过实验发现了非常规的准周期性雪崩式应变爆发.Csikor 等[14]通过三维位错动力学（Three-dimensional discrete dislocation dynamics,3D−DDD）模拟和相应变形行为的统计分析，确定了位错雪崩过程中应变变化的分布，并建立了其对微晶尺寸的依赖关系.上述研究揭示了发生应变突增或者应力陡降的内在原因，并基于模型和理论表征其规律性，然而未分析加载方式对间歇性行为的影响.Cui 等[15−16]在3D−DDD 模拟中通过调整外部加载方式，发现单晶铜微柱的力学行为从力控制下的应变爆发转变到位移控制下的准周期振荡.上述工作尚未分析不同加载方式下力学特征转变的位错机理.

在类似碰撞和冲击的高应变率服役环境中，亚微米单晶铜应变率相关的位错基动态变形机制已成为重要的研究方向[17−18].Jennings 等[19]通过实验研究纳米单晶铜在不同应变率下的拉伸和压缩行为，发现了流动应力的应变率敏感性随着晶体尺寸的减小和应变率的上升出现转变，其原理被认为是位错机制从单臂位错源增殖变化到表面形核.Zheng 等[20]在传统二维离散位错动力学（Twodimensional discrete dislocation dynamics,2D−DDD）模型中引入热激活位错逃逸机制，分析了应力松弛和蠕变过程中钛合金的应变率敏感性行为.然而，上述研究仅仅聚焦纳米尺度晶体和低应变率下变形行为.郭祥如等[21]基于3D−DDD 分析单晶镍压缩变形过程中流动应力和变形机制的应变率效应，揭示了更高应变率下有效应力代替位错源激活应力成为流动应力的主要部分这一机理.Agnihotri 与Van der Giessen [22]的多晶铜拉伸变形的工作也表达相同的观点，但是没有基于理论解析的具体量化分析.

传统的连续介质力学理论缺乏材料的內禀长度参数，无法描述亚微米尺度位错形核、运动、湮灭等一系列演化反应[23]，为了简化计算模型，提高处理晶体材料的计算效率，本文主要采用2D−DDD 模型来研究单晶铜不同加载方式和应变率的塑性流动问题.通过与微压缩的位移加载实验结果对照，验证了模型的可行性.在此基础上，将加载方式与位错演化联系起来，解释了不同加载方式对应的特征应力−应变曲线，揭示了高应变率对单晶铜位错演化和屈服应力的影响，确定了应变率敏感性行为转变机制.

1 单晶铜二维离散位错动力学模型

1.1 二维离散位错动力学框架

离散位错动力学是以晶体材料弹性连续介质中线缺陷-位错为研究对象，通过对滑移系中大量位错的集群运动和相互反应的显式表达，描述塑性变形特征的微尺度力学建模方法.2D−DDD 模型，如图1（a），忽略三维位错交割和螺位错交滑移等交互作用机制，将三维位错线投影到二维平面上，简化为平面模型中一个伏尔特拉（Volterra）奇异点，通过关注刃型位错点的受力、运动和演化，研究微尺度晶体塑性变形行为.

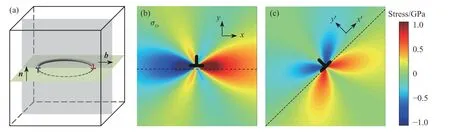
图1 位错的二维简化及其应力场.（a）位错线在二维平面的投影示意图；（b）水平方向和（c）倾斜45°方向正刃型位错剪切应力场Fig.1 Two dimensional simplification of and stress field of dislocation:(a) planar representation of the dislocation line on a 2D plane;stress field (σxy)around a positive edge dislocation in the (b) horizontal direction and (c) tilt direction with an angle of 45°

晶体中位错受到的应力来源主要是外部作用和模拟区域内位错间的相互作用.根据施密特（Schmid）定律，计算外部载荷在滑移系上对位错的分解剪切应力[24]，位错间的相互作用是通过位错弹性应力场起作用，2D−DDD 中刃型位错在无限大介质中的应力场公式如下[25−26]：

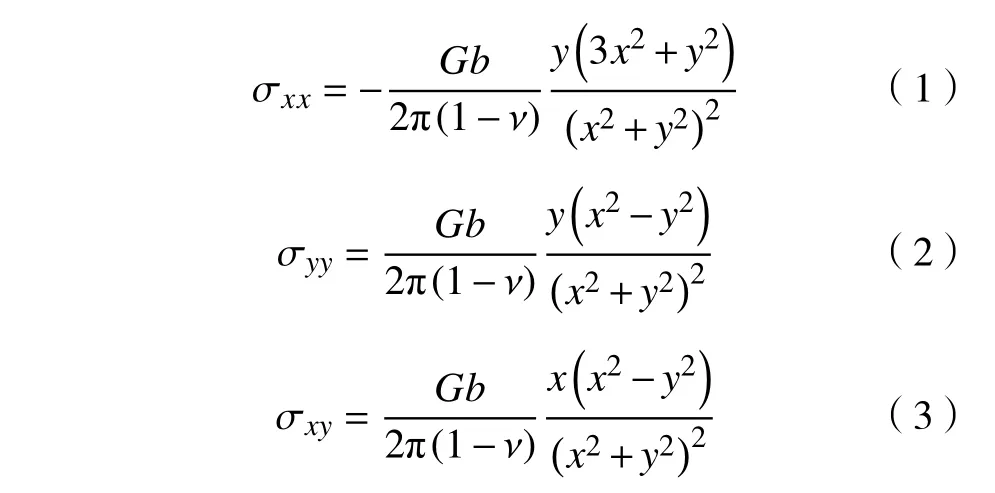
其中，σxx,σyy,σxy分别是位错在x方向、y方向的正应力以及剪切应力，Pa；ν是泊松比，量纲为一；（x,y）是模拟区域任意点相对位错的位置，（m，m）；G和b分别为晶体材料的剪切模量(Pa)和位错的伯格斯（Burgers）矢量的模，m.由于位错间的相互作用的计算基于水平且平行的两滑移面，在倾转滑移系下应力场的计算需要考虑坐标系x−y和滑移坐标系x′−y′两个系统应力张量的变换，具体公式如下[26]：

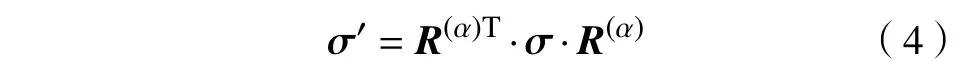
其中，σ为坐标系x−y下的应力张量，σ′为滑移坐标系x′−y′下的应力张量，R(α)为产生应力场的位错所在滑移系α的坐标旋转矩阵：

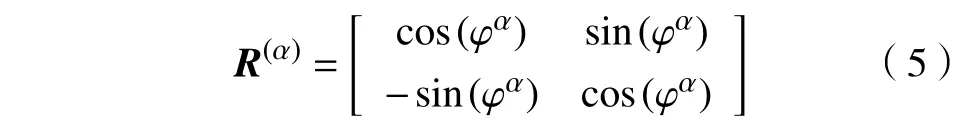
其中，φα是滑移系α中x′方向相对x方向的倾斜角度，（°）；应力场旋转结果如图1（b）和图1（c）所示.图中，n代表位错环所在滑移面的单位法向，b表示位错的Burgers 矢量.

由于位错与边界以及位错之间强相互作用，位错结构热力学不平衡态驱动位错沿滑移系运动并重新分布，基于最小势能原理，位错运动的热力学构型力，即位错皮奇−凯勒（Peach−Koehler）力为：

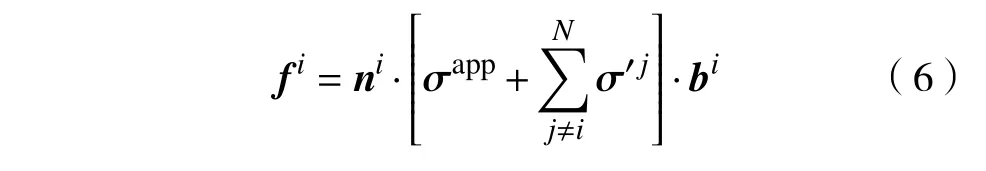
其中，ni表示位错i所在滑移面单位法向，bi表示位错i的Burgers 矢量，σapp表示外部作用应力张量，求和项表示所有N个位错j对位错i的长程作用应力张量.

当施加在位错上的驱动力大于阻碍力时，位错开始运动，主要包括滑移和攀移.位错滑移是连续弹性介质场中位错沿晶体特定滑移系运动的保守运动，而位错攀移是在垂直滑移面通过吸收和释放点缺陷实现位错扩散运动的非保守运动[27].通常在非高温变形环境下，位错运动形式以滑移为主.在Peach−Koehler 力作用下，考虑到位错运动处于过阻尼状态，每个位错段的速度由作用在其上的总力和黏滞阻尼系数决定，即位错i的滑移速度表示为[24,28]：

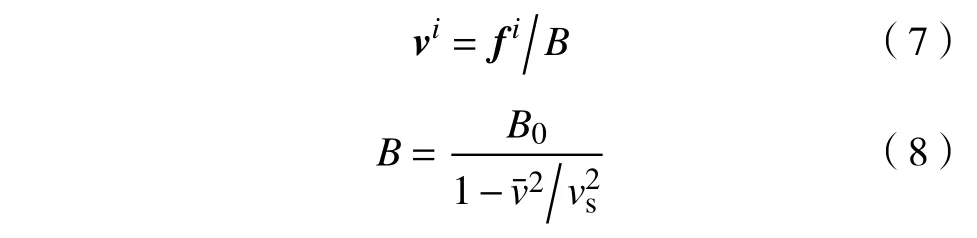
其中，vi是位错i的滑移速度，m·s−1；B为位错滑移的黏性阻尼系数，N·s·m−1；fi为作用在位错i上的Peach−Koehler 力.v¯是位错平均速度，m·s−1；vs为剪切波速，m·s−1.当位错运动速度较低时，采用静态黏性阻尼系数B0，N·s·m−1.

经历剧烈塑性变形后的金属晶体，其位错密度可增加4～5 个数量级，说明晶体在塑性变形过程中必然发生着位错增殖.其中，弗兰克−瑞德（Frank−Read）位错源形核是内部位错增殖的一种主要方式.2D−DDD 方法将位错源简化和近似成滑移面上一点，当作用在点源上的分切应力τ大于临界形核强度τnuc并保持临界发育时间tnuc后，一对带有异号Burgers 矢量位错偶极子形核在位错源点两侧，其分布极性与分切应力方向对应.为使位错源开动，作用在位错源的分解切应力需克服位错线弯曲时的线张力.根据奥罗万（Orowan）应力判据[21]，位错源静态平衡破坏需要的临界切应力为：

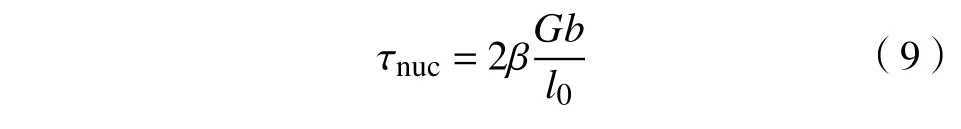
其中，β为一个量化参数，对Frank−Read 源，β≈1，l0为位错源初始长度，m；与晶体尺寸有关.l0满足一个均值和标准差Δl0的高斯分布，以确保位错源强度在一定范围内变动.

位错临界形核时间为[22,29]：

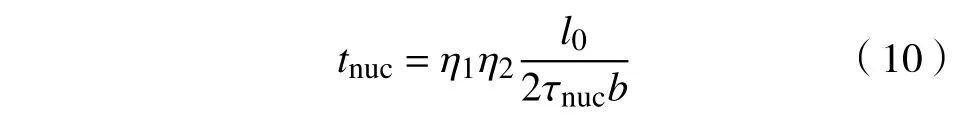
其中，η1是描述位错从半椭圆到完全位错环的增强因子，η2为与黏性阻尼系数B有关的常数，Pa·s.

一对偶极子的临界形核距离Lnuc由临界形核应力确定[25]，从而确保当一对位错偶极子产生，作用偶极子上外部分解切应力正好与偶极子之的间互相吸引应力平衡：

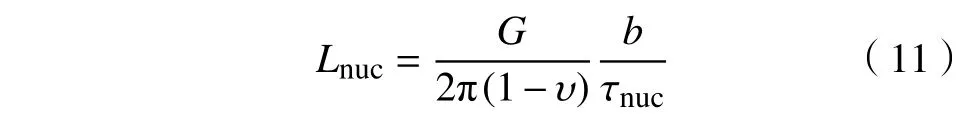
当同一滑移面中一对异号位错互相吸引并靠近会发生湮灭，在2D−DDD 模型中，设置当正负位错相互距离小于临界距离Lanni，位错发生湮灭.Lanni是材料相关参数，m；在计算中一般取Lanni=6b[30].

1.2 离散位错动力学模型的数值实现

本研究中离散位错动力学模型计算流程如图2 所示，采用前向欧拉积分算法以时间增量步的方式进行.在每个增量步中，需要的计算主要是：①确定当前位错的构型、应力和应变状态；②根据位错所处应力状态计算位错运动Peach−Koehler 力；③根据式（7）～（11）的本构法则处理位错运动、Frank−Read 源形核、异号湮灭等短程位错构型的变化.为了提高计算效率，节约计算成本，根据应变率和计算总应变确定固定时间步增量.同时，为了考虑实际情况位错不会超过前面位错的特点，计算中需要对相邻位错判断，若当前时间步内发生位错越过现象则需要对位错速度进行修正.本文主程序基于Matlab 平台编写，使用C 语言编写的mex 子程序计算位错间相互作用.

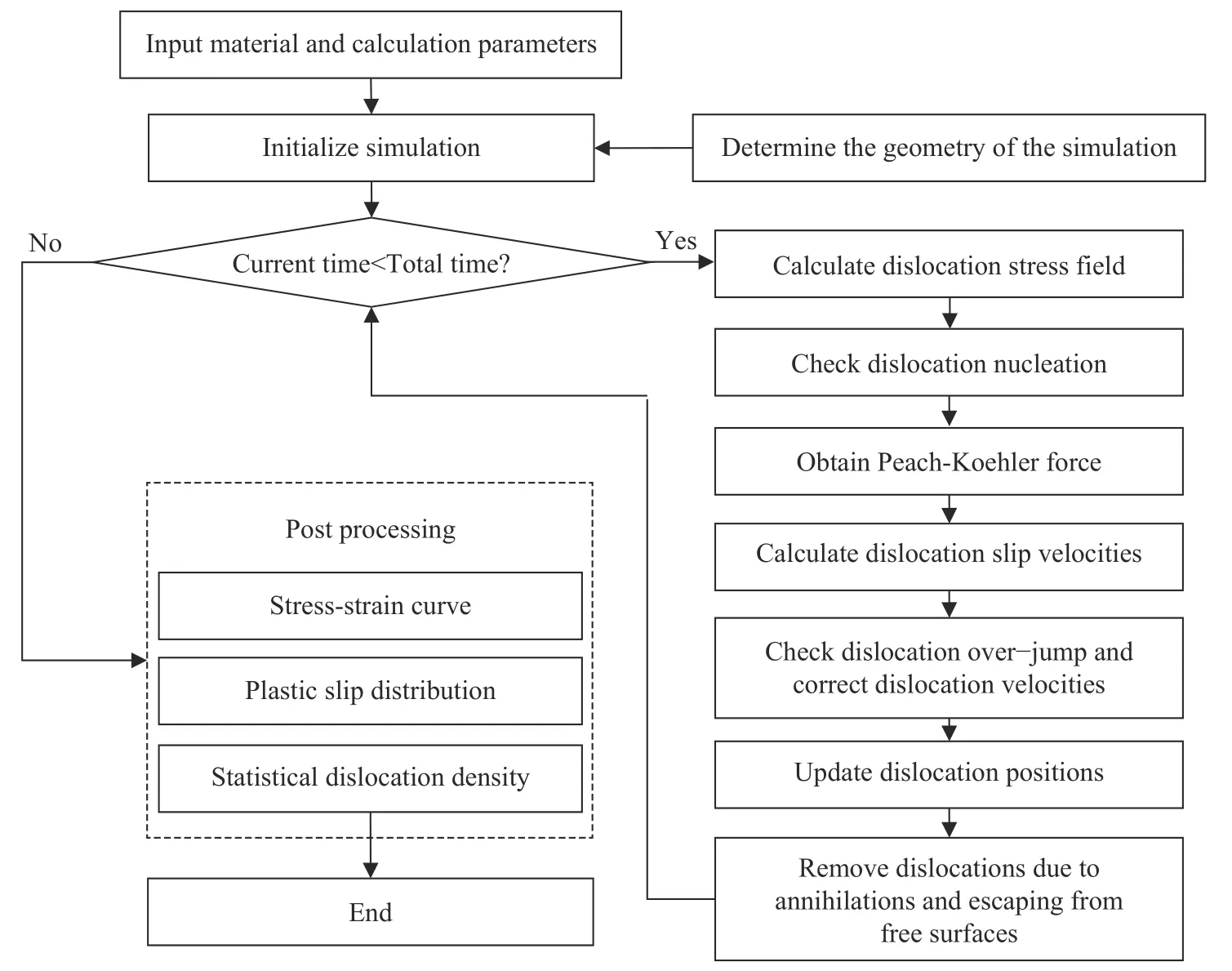
图2 2D−DDD 模型的模拟流程Fig.2 Flow chart of the 2D−DDD model

小应变假设下的2D−DDD 模型，忽略了试样有限变形诱导晶格转动和形状改变对滑移动量平衡的影响，因此计算过程中应变一般不超过0.01.总塑性应变率是所有滑移系位错运动的贡献之和：

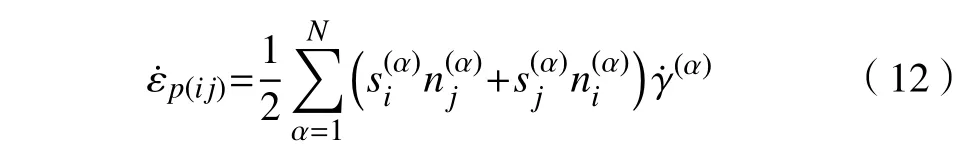
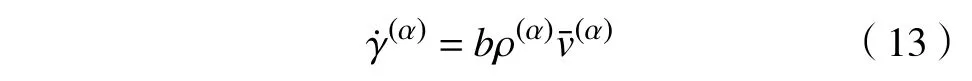
其中，ρ(α)为滑移系α上位错密度，m−2；v¯(α)为滑移系α上位错平均速度，m·s−1.

1.3 单晶铜塑性变形过程2D−DDD 模型的建立

为了分析不同加载方式和应变率对位错运动的影响，并且验证2D−DDD 模型的准确性，本文以崔一南建立的3D−DDD 模型[15−16]为参照，并与之进行对比并建立2D−DDD 模型.初始化设置主要包含材料参数和模型计算参数初始化，以及几何构型初始化两个部分.本研究对象单晶铜具体的模拟参数如表1 所示.几何构型初始化主要是确定模拟区域的尺寸、滑移面取向与排列、位错源的位置分布以及边界条件等方面.

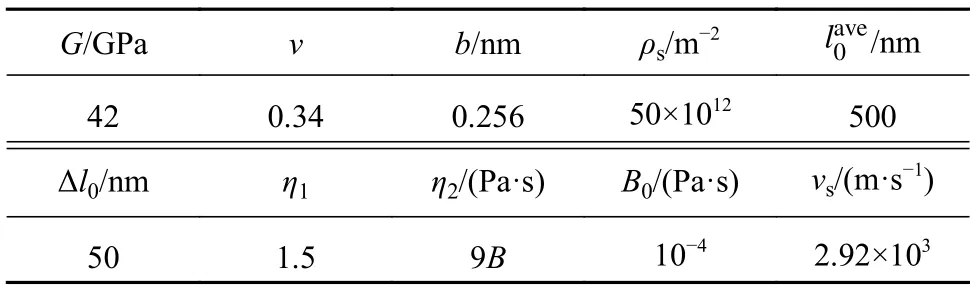
表1 单晶铜2D−DDD 模拟参数Table 1 Model parameters used in the 2D−DDD model for single crystal copper

如图3 所示，模拟区域晶体尺寸为1 μm×3 μm.单晶铜是面心立方（Face−centred cubic,FCC）材料，模拟系统的x轴和y轴分别沿着和[001]方向[31]，考虑到平面应变状态的3 种主动滑移系的相对夹角近似为{0°,±60°}，由于0°取向的滑移系的Schmid 因子为0，因此忽略0°滑移系，选取的滑移方向分别与x轴成±60°，滑移面间距设定为150b.模拟平面内无初始位错，位错源随机分布在滑移系上，为保证多滑移系变形均匀，两个滑移系上的位错源数目设置相当.对于单晶微柱试样，模拟区域的左右边界视作不可逾越的障碍.为了避免数值计算的复杂性，参考通用的模型简化方法和实验微柱压缩形态[31−32]，与左右约束端相交的滑移面在模型中没有考虑，而上下边界对应为微柱的自由表面，位错运动到上下边界不仅要计算位错所受镜像应力还要考虑位错的湮灭.

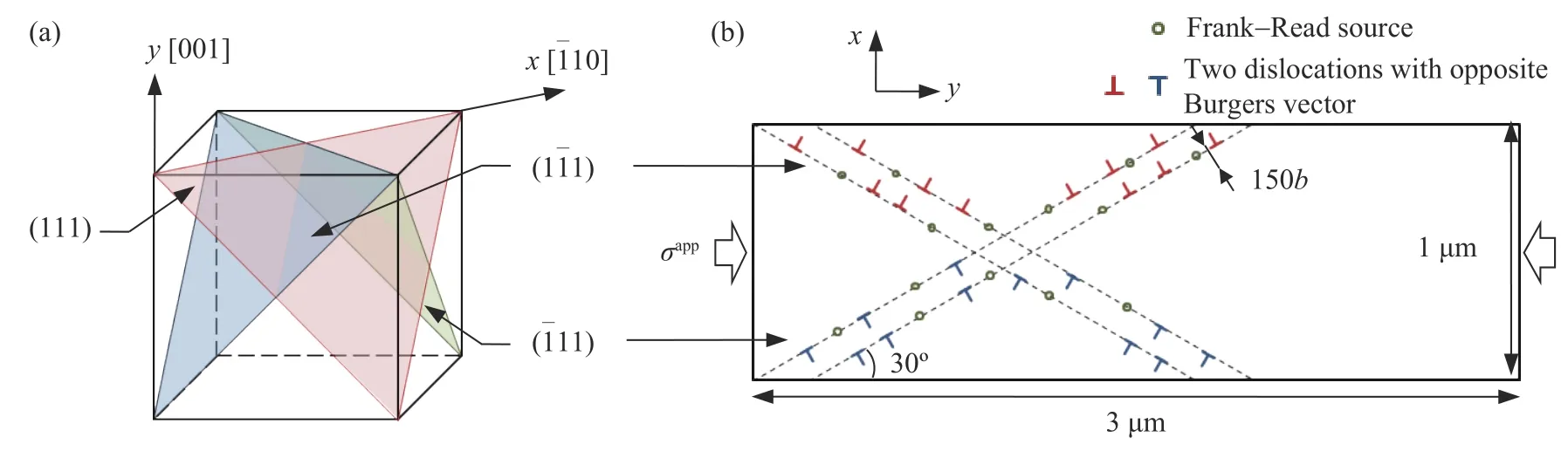
图3 单晶铜晶体学取向及计算模型.（a）FCC 晶体滑移系取向；（b）压缩载荷下2D-DDD 计算模型Fig.3 Crystallographic orientation and calculation model of single crystal copper:(a) slip system orientation for the FCC crystal;(b) the 2D−DDD model under compression

初始化完成后，沿着[001]方向进行压缩加载，以实现多滑移条件.为对比不同加载方式的作用效果，分别采用位移加载和力加载方式.位移控制加载时选择恒定应变率为1000 s−1，根据胡克定律可将其转变为外力增长率 σ˙app：

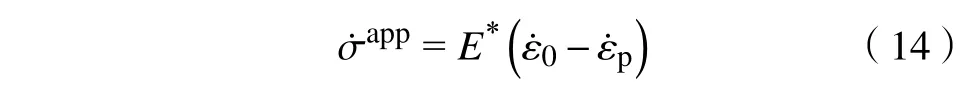
其中，E*为二维模型在平面应变条件下的/杨(氏模)量，Pa；考虑到平面应变的情况，E∗=E1−ν2，E为一般杨氏模量，Pa；为加载应变率，s−1；是塑性应变率，s−1.

力控制加载时，设定力增加率为一个恒定值，对应式（14）位移控制加载方式，初始塑性应变率为0.在离散位错动力学模拟中，Rao 等[33]提出了一种利用截断塑性应变率控制力加载的方式，将其与材料内部位错的运动联系起来.即对位错的运动设置一个塑性应变率阈值，当位错运动引起的塑性应变率低于该阈值时，以恒定应力速率加载，反之，外加作用应力不再增加，即力增加率为0.这种方式需要确定临界塑性应变率和应力增量的大小，可能会影响位错雪崩的大小.本文中利用加权位错速度的方式[15−16]来控制应力的加载，与塑性应变率控制类似，存在一个加权位错速度阈值vth，当加权位错速度vw低于该临界值时，力加载正常进行.反之，当位错爆发式运动，加权位错速度vw高于该临界值时，应力保持恒定不变.位错速度阈值vth和加权位错速度vw的计算公式如下：

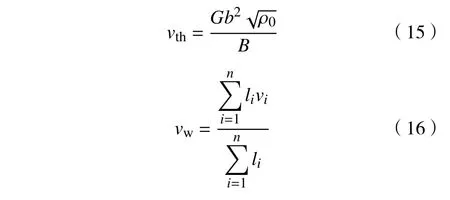
其中，ρ0为初始位错密度，m−2；这里采用位错源密度表示，li表示位错段i的长度，m；vi表示位错段i的速度，m·s−1.在2D−DDD 模型中，每个位错均是等效的无限长，加权位错速度vw即是平均位错速度，m·s−1.

2 模型验证

基于不同加载方式的单晶铜2D−DDD 模型计算得出力控制和位移控制加载的力学曲线，如图4所示.两种加载方式下，单晶铜的最高应力水平均在100～120 MPa 范围内，初始塑性变形应力在90 MPa左右，近似与Frank−Read 位错源形核应力的均值（99 MPa）对应，说明此时位错开始以位错源激活的方式增殖并贡献塑性应变.在经历一段纯弹性变形行为后，塑性阶段流动响应都呈现很强的不连续性，并且这种不连续的应力−应变曲线的形状不同：位移加载时，应力−应变曲线呈现准周期的锯齿状；力加载时，应力−应变曲线呈现应力单调增加的台阶状.这些不连续性的力学特征反映为微观的位错剧烈演化，随着位错增殖或运动显著，真实的塑性应变呈现爆发式增长.

这种现象已经在很多微拉压实验和模拟中被发现[34−35]，通过与Cui 等[16]3D−DDD 模型中力加载和实验[36]中位移加载稳定流动应力范围的对比，模型预测在误差允许范围内吻合良好，定量化地验证本模型的可靠性.本工作将应变率为103s−1时2D−DDD 的预测结果与实验的准静态压缩结果相对比，远远高于实验中采用的应变率，因为在离散位错动力学中，应变率小于103s−1时均可认为准静态条件，应变率可以在一个很宽范围并且计算结果不再受应变率的影响[21].由于单晶铜单轴压缩实验的微柱尺寸（800 nm）和3D−DDD 模型尺寸（3000b）小于本模拟尺寸参数，而且2D−DDD 模拟忽略了位错攀移和交滑移等三维机制对塑性变形的影响，因此可能导致模拟结果相较于实验和其他模拟流动应力偏小.

3 结果和讨论

3.1 加载方式对单晶铜力学行为的影响

为了对比两种加载方式下单晶铜应力−应变曲线形状的差异及解释其内在机理，以上述加载条件为例，单独研究发生一次位错雪崩的情况，如图5 所示.在力和位移控制加载下，发生一次位错雪崩事件时力学响应呈现不同的形式，前者为应变的陡增，后者为应力的陡降.具体表现为，一次位错雪崩时，力加载时的应变陡增，对应的应变增量为0.02%，而应力在此时几乎无变化；位移加载时的应力突降，对应的应力增量为12.89 MPa，而应变在此时几乎无变化.

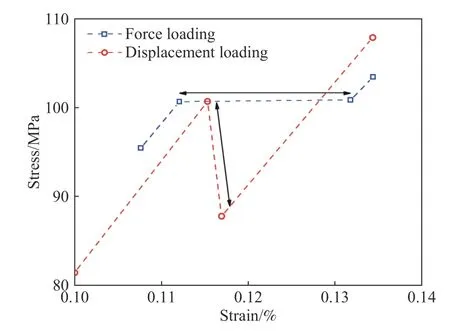
图5 不同加载方式下发生一次位错爆发的应力-应变曲线Fig.5 Stress-strain curves of dislocation avalanches under different loading modes

力加载时，图6（a）对比加权位错速度和应力随应变的变化曲线，可以看出，应力−应变曲线发生应变突增时，加权位错速度与位错速度阈值相等.由于外加力的增长是通过加权位错速度来调节，当加权位错速度超过位错速度阈值时，恒定速率上升的外加应力停止增加，此时相当于保载条件下位错弛豫过程，位错依靠自组织演化，根据公式（13），持续贡献塑性应变，速度抖动地下降；当加权位错速度低于位错速度阈值时，外加应力率大于0，应力继续增加，直至加权位错速度再次达到位错速度阈值，以上过程重复.因此，在一个完整的位错雪崩阶段，外加应力保持稳定，而塑性应变持续增加，应力应变响应表现为台阶状，就出现了应变增量大而应力增量几乎为0 的现象.

位移加载时，通过对比塑性应变率变化曲线以及应力−应变曲线，如图6（b），每次应力陡降的发生都出现在塑性应变率等于外加应变率的时候.根据载荷施加公式（14），塑性应变率较小且低于加载应变率时，外加应力速率大于零，应力持续增加，晶体内位错和位错源受力逐渐增大.在满足临界形核强度并保持临界发育时间后，位错源激活驱动位错增殖，位错密度逐渐增大，塑性应变率随之上升；当塑性应变率高于加载应变率，应力增长率小于零，外加应力下降，位错源的受力不足以继续增殖位错，塑性应变率随之下降.直至塑性应变率再次低于应变率加载率，以上过程重复.因此，位错源激活诱发位错雪崩发生时，通过降低外加应力的大小以匹配塑性应变率和加载应变率，就出现了应力增量变化大的现象.

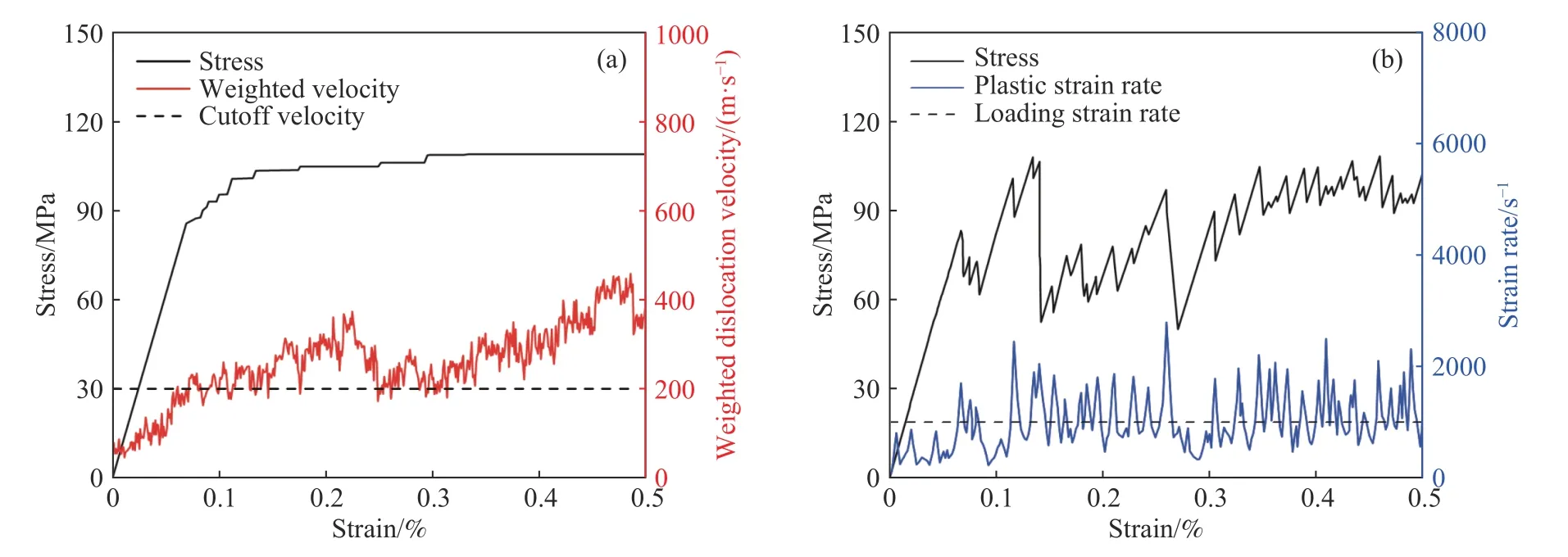
图6 （a）力控制加载下应力和加权位错速度随应变演化；（b）位移控制加载下应力和应变率随应变演化Fig.6 (a) Evolution of stress and weighted dislocation velocity with strain under stress-controlled mode and (b) evolution of stress and strain rate with strain under strain-controlled mode

对于应力控制的外部载荷，位错运动相对速度阈值调控外加载荷的增加和停止，因此位错雪崩效应归结于位错速度的随机性；而当外部约束为位移控制时，由于位错源对形核强度和形核时间的要求，各个位错源的开动表现为间歇性，位错雪崩由位错源交替的开动和停滞主导.

3.2 应变率对单晶铜力学行为的影响

当位移加载时，应变率的大小会影响材料的屈服应力.本文利用2D−DDD 模拟，研究不同应变率下位错演化对单晶铜塑性变形的影响.图7（a）为4 种不同应变率（102、103、104和4×104s−1）的应力−应变曲线，由于模型初始无位错的设置，所以不同应变率下都经历一个完整重复的弹性阶段.将0.1%塑性应变处设置为初始屈服点[22]，提取各应变率下的屈服应力，如图7（b）所示，屈服应力随应变率的增大而增大，呈现典型的正应变率敏感性行为.然而高应变率（104和4×104s−1）的屈服强度与其他应变率相比具有明显的差别.一些文献[22,37]也反映了相似的力学行为，屈服强度的应变率关联性被分成两个作用域，在应变率低于103s−1的第一作用域，屈服强度随着应变率保持着相对稳定，而在更高应变率范围的第二作用域，屈服强度随应变率显著提高.这两个作用域机制一般被解释为：在较低应变率下位错以热激活方式越过障碍，转变为高应变率下的位错阻尼运动.然而，这些理论一般适用于讨论宏观块体或者介观多晶等晶体内位错密度较高的情况[8,22,37].为了分析不同应变率下微米单晶力学行为转变的位错机理，基于上述的模拟结果并通过解析方法进行定量分析.

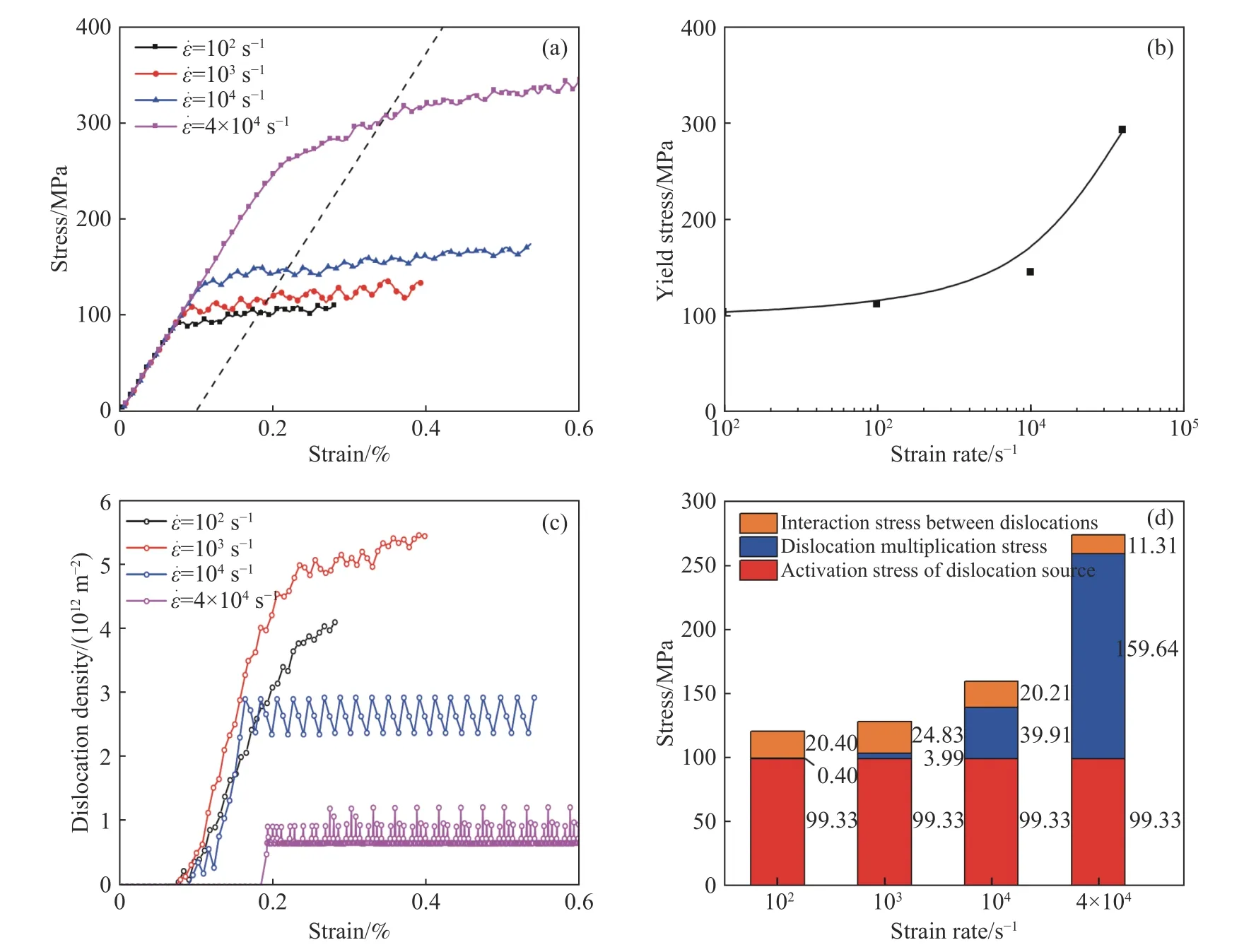
图7 不同应变率下的（a）应力−应变曲线；（b）屈服应力；（c）位错密度−应变曲线；（d）组成应力Fig.7 Effect of strain rate on the evolution of：(a) stress vs strain;(b) yield stress;(c) dislocation density vs strain;(d) stress composition

图7（c）展示的是不同应变率下位错密度随应变演化曲线，整个应变率范围单晶铜屈服时的位错密度都没有超过1013m−2，由位错密度增加的滞后性可以看出，当滑移系上分解切应力达到位错源激活强度并经历一定形核时间后，位错增殖才会开始发生.在低于103s−1的应变率范围内，位错密度随着应变率增加而增加；而在更高应变率下，位错密度随应变率的增加而降低，且其演化的波动性增大.考虑应变率对位错增殖和位错运动的作用，位错滑移贡献的塑性滑移被量化为每个滑移系上分解剪切应变的总和，不同应变率下的滑移量分布如图8 所示.随着应变率的上升，屈服时单晶铜更多的滑移面被激活，塑性应变在各个滑移面分布越来越均匀，说明单一滑移面上位错源形核时间的限制促使其他滑移面位错源的开启，应变率的增加对位错增殖具有显著的促进作用.在103s−1应变率以后的滑移面开启量趋于饱和，此时位错增殖速率不再明显增加，而高应变率下外加作用力增加，位错滑移速度加快导致滑出自由边界更加容易，晶体内位错密度降低，并且间歇的增殖和快速的滑出湮灭也会导致位错密度演化的波动性增大.类似于单晶微柱变形出现尺寸效应的“位错匮乏”机制，即使多数滑移面的位错源开启，也不能满足施加的应变率.

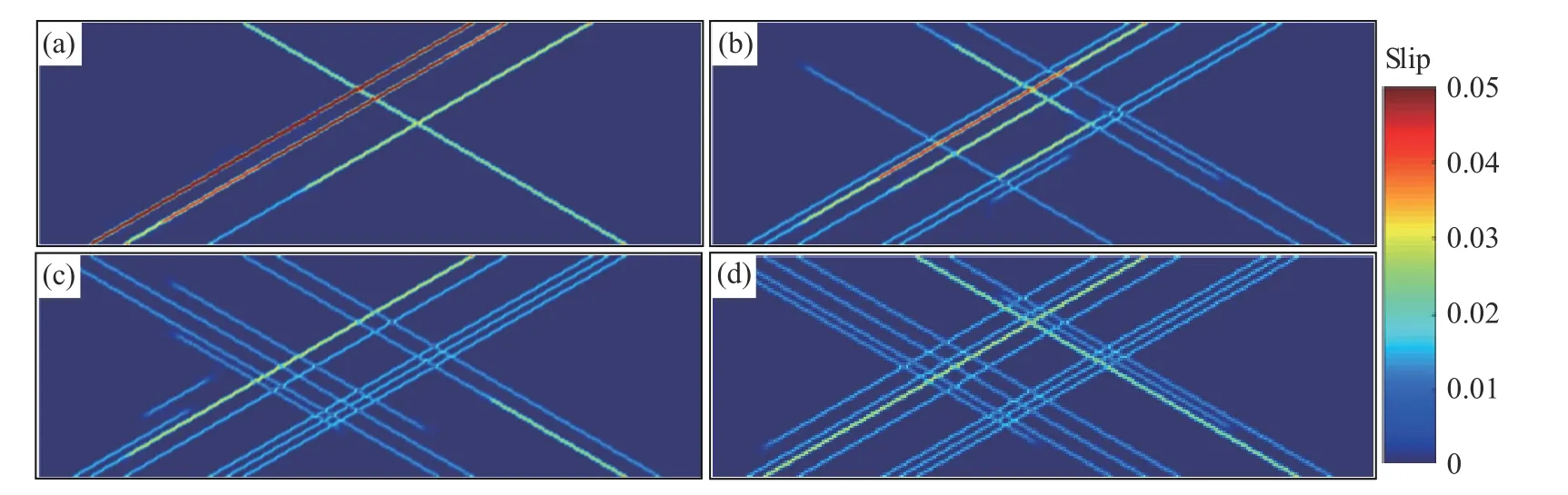
图8 不同应变率下塑性滑移量分布.（a）102 s−1；（b）103 s−1；（c）104 s−1；（d）4×104 s−1Fig.8 Plastic slip distribution resulting from the strain rates at:(a) 102 s−1;(b) 103 s−1;(c) 104 s−1;(d) 4×104 s−1

本文进一步分析了屈服时位错流动应力的组成，以确定不同应变率下单晶铜力学行为.单晶铜流动应力τ等于位错运动的热应力τth和非热应力τa之和[38]：

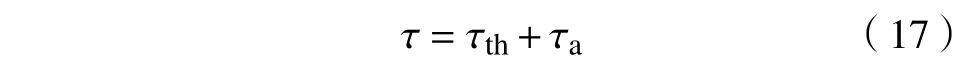
其中，τth是施加在位错上的热应力项，Pa，控制位错的热激活行为，使位错借助自身的能量起伏，越过包括派尔斯（Peierls）障碍等能垒的过程；τa是作用在位错上的非热应力项，Pa，它的来源是位错间的长程弹性相互作用力和位错源形核相关应力.对于面心立方晶体，在正常温度和应变率条件下，热应力项τth来源主要是Peierls 障碍，大约为0.5 MPa，位错很容易克服该障碍.因此，热应力项τth的影响可以被忽略，流动应力τ主要由非热应力项τa提供.根据泰勒（Taylor）硬化法则和公式（9），非热应力项τa可以表示为[39-40]：

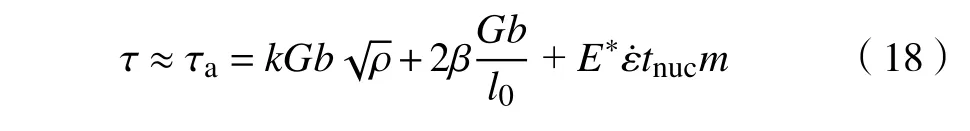
其中，第一项为位错密度相关的相互作用力，k为量纲一常数，一般取值为0.5；ρ是位错密度，m−2；第二项为基于Orowan 应力判据的位错源激活应力；第三项是位错增殖应力，与位错形核时间相关，是加载应变率，m·s−1；m为Schmid 因子.对于位错增殖应力项[22]，一旦外加应力满足第二项的位错源形核强度，被激活的位错源需要一段形核时间tnuc去产生一对偶极子才能完成一个完整的位错增殖过程.在此时间间隔内，弹性应变增加，因而贡献了流动应力的上升.

基于解析表达式（18）和位错密度参数，不同应变率下单晶铜屈服应力组成如图7（d）所示.解析表达式计算得到的屈服应力与图7（b）中2D−DDD 模拟的结果吻合较好.其中，102～104s−1应变率下模拟屈服应力略低于解析计算值，这是因为解析表达式的位错源激活应力以初始位错源长度均值500 nm 计算的，为保证各滑移面上位错源不会同时激活，位错源长度满足一个高斯分布，因而初始激活的位错源强度一定小于均值99.33 MPa.

值得注意的是，在4×104s−1应变率时，模拟屈服应力反而略高于解析计算值，这里归因于位错阻尼运动受力，通过两种方法计算4×104s−1应变率时屈服应力的差值估计，位错运动阻尼力稍大于18.27 MPa，表明阻尼作用并不是高应变率屈服应力的主导机制.阻尼力来自位错与晶格热振动之间的相互作用，可表示为：.其中，γ˙为剪应变率，s−1.可见，在具有一定位错密度的晶体内，随着位错运动速度增加，电子和声子对位错运动的阻力也会随之增大.然而，加载应变率越高，小尺寸试样中的位错越容易在滑移时从自由表面逃逸，并且位错逃逸的速度会超出位错增殖的速度，晶体尺寸效应开始显著[7]，由图7（c）可知，高应变率下的位错密度大大降低.此时，阻尼力计算值趋向于无穷大，与位错运动相关的阻尼力公式无法合理表达流动应力贡献.

应变率从102s−1到4×104s−1，位错源激活应力在屈服应力中占比逐渐减小，位错增殖应力逐渐增大，说明屈服应力的应变率敏感性机制从位错源激活转变为位错增殖.低应变率下位错通过更多的滑移面位错源激活来贡献塑性应变，位错源激活应力只与位错源初始长度有关，与应变率无关，所以随着应变率增加，屈服强度保持相对稳定.在较高的应变率下，有限的内部源无法产生足够的塑性来抵抗外部加载的增加，位错增殖成为屈服应力增加的主要因素，位错增殖应力与应变率密切相关，因而随着应变率增加，屈服强度显著增加.三维模拟也说明相似的现象，反过来，这些内部位错源可能由于应力的增加而被破坏，位错增殖机制会从内部Frank−Read 位错源转变为表面形核[18].