散射光对基于Bi-EDFA的分布式光纤传感器信噪比的影响
2021-10-23史衍方陈永超宋秋衡
史衍方,陈永超,宋秋衡,肖 倩,唐 璜,贾 波
(复旦大学 材料科学系,上海 200433)
分布式光纤传感器作为一种新型传感器,可用于复杂环境中的动、静态物理量测量,它具有结构简单、高精度、高灵敏度、抗电磁干扰等众多优点[1].与基于反射光的布拉格光栅(Fiber Bragg Grating, FBG)和基于后向散射光的布里渊光时域反射仪(Brillouin Optical Time Domain Reflectometer, BOTDR)相比,依赖于相位变化的光纤干涉仪具有更快的响应速度和更高的灵敏度[2],常用于长距离传感监测.在长距离的光纤系统中,通常会使用掺铒光纤放大器(Erbium-Doped Fiber Amplifier, EDFA)来补偿光纤中信号光的过度损耗.因此,EDFA的工作状态是影响信号传输距离和系统信噪比的关键因素之一[3-4].
在传统的长距离光纤传感系统中[5],信号传输往往都是单向的.为了满足双向传输的需求,双向掺铒光纤放大器(Bidirectional Erbium-Doped Fiber Amplifier, Bi-EDFA)[6-7]得到研究开发,它可以同时对正向光和反向光进行放大,尤其对于线型Sagnac干涉仪具有重要意义.线型Sagnac干涉仪是单芯传输[8-9],它不仅节省了光纤资源而且简化了系统结构,在长距离传感监测中广泛应用,如管道泄漏监测、周界安全监测以及光缆故障监测等[10-12].为了抑制长距离传感线路中色散带来的影响并提升信号传输距离,可以在线路中添加一段色散补偿光纤(Dispersion Compensation Fiber, DCF)[13].但是与单向EDFA相比,为了实现双向放大功能,Bi-EDFA输入和输出两端没有隔离器,因此线路中产生的散射光不可避免地会对Bi-EDFA造成一定影响[14].而DCF中的散射特性与单模光纤(Single Mode Fiber, SMF)中的不同,它对于Bi-EDFA的影响是未知的,这是将DCF用于补偿传感线路色散时存在的主要问题,目前很少有文章对此进行研究.
因此,本文利用线型Sagnac干涉仪,研究并对比了带有色散补偿光纤线路的和仅有单模光纤线路的散射光对基于Bi-EDFA的光纤传感器性能的影响.理论分析并实际测试了DCF和SMF中产生的散射光大小;理论推导并实验记录了系统信噪比值.针对SMF-DCF、SMF-SMF和SMF-DCF-SMF 3种传感链路组成情况,对比分析了不同信号光强度下系统信噪比的变化趋势.
1 系统结构
本文所研究的基于线型Sagnac干涉仪的分布式光纤传感系统结构如图1(见第474页)所示.光源采用相干长度为微米量级的超辐射发光二极管(Super Luminescent Diode, SLD).FWDM(Filter Wavelength Division Multiplexer)是信道间隔为200 GHz的波分复用器.3×3耦合器(C1)和2×2耦合器(C2)将光信号分为沿顺时针和逆时针传播的两部分,时间延迟光纤(Time Delay Fiber, TDF)用于在这两条传播路径中产生固定时间差.

图1 基于线型Sagnac干涉仪的分布式光纤传感器Fig.1 Distributed optical fiber sensor based on line-structure Sagnac interferometer
在传感部分,利用两个双向放大器(Bi-EDFA1, Bi-EDFA2)对信号光进行调节.为了对比带有色散补偿光纤线路与仅有单模光纤线路的信噪比区别,传感链路(Sensing Link, SL)采用3种连接方式: (a) 由80 km SMF和8 km DCF组成;(b) 由80 km SMF和20 km SMF组成;(c) 由40 km SMF、8 km DCF和40 km SMF组成,分别如图1(a)、(b)和(c)所示.由于单模光纤和色散补偿光纤的衰减分别为0.2 dB/km和0.5 dB/km,8 km DCF可替换为20 km SMF,两者损耗一致可作为对照实验.在1 550 nm窗口,单模光纤的正色散值为17 ps /nm·km;相对地,色散补偿光纤有约为-150 ps/nm·km的负色散值.LiNbO3相位调制器(Phase Modulator, PM)和信号发生器(Signal Generator, SG)对光相位起电光调制作用.法拉第旋转镜(Faraday Rotator Minor, FRM)用于控制光路偏振特性并反射光波.最终,光信号由光电探测器(Photo Detector, PD)接收,并由采样率为2.5 GSa/s的示波器进行采集用于LabVIEW程序的信噪比分析与计算.在图1所示的传感系统中,共有4条传播路径可以进行光传输:
Ⅰ: 1→4→TDF→6→8→9→10→11→12→FRM→12→11→10→9→8→7→5→C1
Ⅱ: 1→4→TDF→6→8→9→10→11→12→FRM→12→11→10→9→8→6→TDF→4→C1
Ⅲ: 1→5→7→8→9→10→11→12→FRM→12→11→10→9→8→6→TDF→4→C1
Ⅳ: 1→5→7→8→9→10→11→12→FRM→12→11→10→9→8→7→5→C1
由于SLD光源的相干长度很短,只有路径Ⅰ和路径Ⅲ中的光束最后会在耦合器C1处产生干涉现象.另外有必要指出的是,另一个耦合比为99∶1的耦合器(C3)用来评估进入到Bi-EDFA2中的后向散射光和信号光的大小.光功率由高精度光功率计(Optical Power Meter, OPM)进行测量.
2 理论分析
对于使用Bi-EDFA的分布式光纤传感器,Bi-EDFA的工作状态在系统信噪比上起重要作用.光纤中产生的后向散射光属于系统噪声,而Bi-EDFA不能区分有用光和无用光,因此它会影响Bi-EDFA的有效放大.
2.1 光纤中的后向散射特性
瑞利散射(Rayleigh Scattering, RS)是光纤中散射光的主要构成.RS作为一种线性散射过程,散射光的强度与光纤入射光的强度成正比.在光纤中,由正向、反向传输光组成的电场表达式可以表示为[15]
E=E0eiβz+Ψ(z,β)e-iβz.
(1)
其中:β为传播常数;z为光波在光纤中的传播距离;E0和Ψ分别为正向光和反向光的场振幅.在瑞利散射较弱的情况下,后向散射光的近似解可以表示为
(2)
其中:Ψ(0,β)代表能被检测到的反向光信号;Ψ(z=L,β)为光纤端面反射光的振幅;L为光纤长度;ε为材料的介电常数;Δε为自发散射的局部波动.考虑到光纤衰减系数α,传播常数β应更改为β+iα.通过式(2)可以看出,光纤中后向散射光的强度与光纤损耗有关.而与单模光纤SMF相比,色散补偿光纤DCF具有更高的衰减系数.因此,在入射光相同时,DCF中的后向散射电场要强于相同长度的SMF中的.
2.2 传感器信噪比
由于系统信噪比主要由传感线路决定,接下来对该线路输出端的信噪比进行理论推导,传感线路的简化图如图2所示.

图2 传感线路简化图Fig.2 Simplified diagram of sensing line
假定输入端信号光功率为Pin,Bi-EDFA1与Bi-EDFA2之间损耗为L1,Bi-EDFA2与FRM之间损耗为L2,Bi-EDFA1和Bi-EDFA2对正向光和反向光的增益分别为G1和G4,G2和G3.由于Bi-EDFA要对正、反两个方向上的光进行放大,其两端没有添加隔离器,需要考虑长距离传感链路SL中产生的后向散射光.因此输出光Pout主要由信号光Ps、自发辐射光Pase总和后向散射光Pbs总组成,其中后两项是该系统的噪声信号.这3种光可以分别表示为
(3)
(4)
(5)
其中:L1和L2为与光纤性质相关的常数.对于式(4),自发辐射光Pase=2nsp(G-1)hνBf,其中:nsp为粒子数反转系数;h为普朗克常数;ν为光频率;Bf为滤波器光带宽.Pase1和Pase4,Pase2和Pase3分别是Bi-EDFA1和Bi-EDFA2在正向和反向光放大时产生的自发辐射光.对于式(5),Pbs2是反向信号光在传感链路SL中产生并到达Bi-EDFA2左侧的后向散射光;Pbs1是正向信号光在传感链路SL中产生并到达Bi-EDFA1右侧的后向散射光.
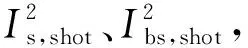
(6)
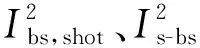
3 实验方法及结果分析
3.1 传感线路散射光的影响分析
为了评估光纤中实际散射光的大小,首先采用基于光环形器(Optical Circulator, OC)的光路系统测试后向散射光与光纤入射光之间的关系,其结构如图3所示.光功率计OPM在环形器3端口处可以测量到光纤段反馈的后向散射光.待测光纤分为两大组.第1组,待测光纤又分为图3(a)、(b)和(c)3种情况.图3(a)和图3(c)是对照组实验,为了研究色散补偿光纤在不同位置对线路整体散射光的影响.图3(b)和图3(a)、(c)对比是为了考察单模光纤线路和带有色散补偿光纤线路的区别.第2组中,仅对图3(a)中第1段8 km DCF和图3(c)中第1段40 km SMF进行测试,与第1组形成对比.测试时首先调节SLD光源强度,使得Bi-EDFA输入光功率为100 μW;然后以每次10 mA的幅度将Bi-EDFA的泵浦电流从200 mA调节到470 mA,并依次对后向散射光进行记录.
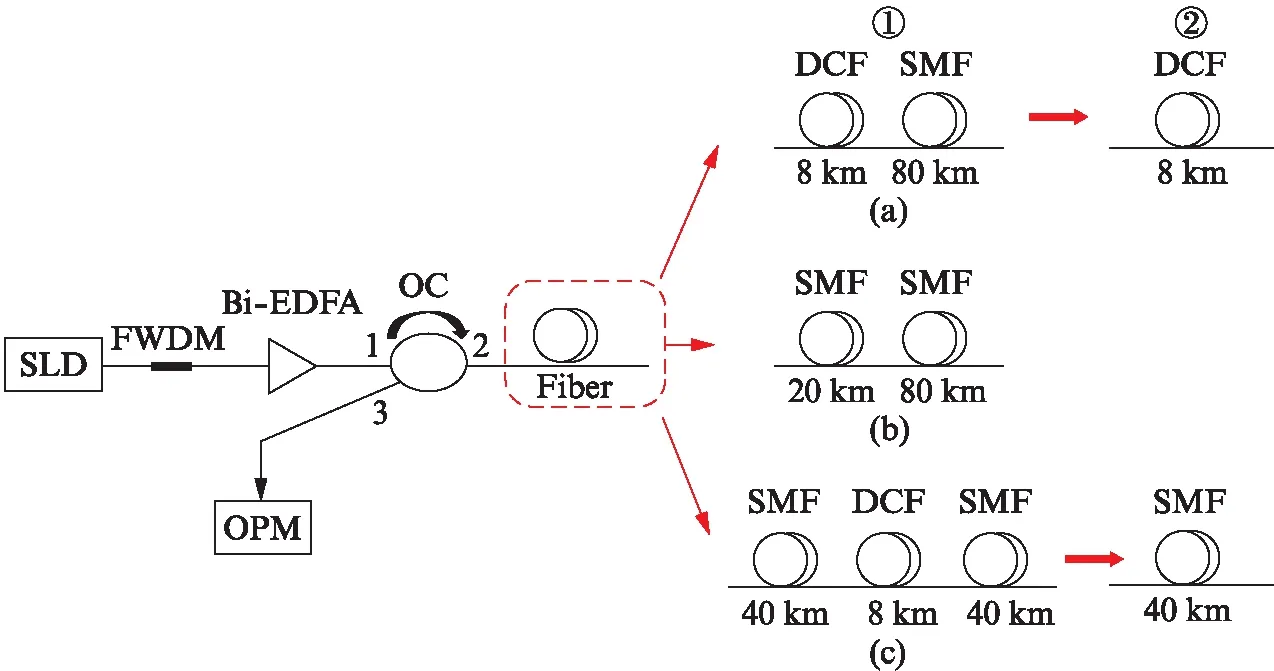
图3 测试光纤后向散射光的系统Fig.3 System for measuring the back-scattered power in fibers
测试结果如图4所示,可见后向散射光大小与入射光强度呈线性关系,其拟合函数也已标记在图中.首先观察图4(a),相同入射光强度下,当色散补偿光纤位于信号入射端时(黑线)后向散射光是单模光纤线路(红线)中的2倍.调整色散补偿光纤位置至两段单模光纤中间可以降低整段线路反馈的散射光强度,接近于只有单模光纤的线路.然后观察图4(b),图中紫线的测量值略高于黑线,是因为测试过程中存在误差.总体上对于DCF-SMF和SMF-DCF-SMF两种情况,线路整体反馈的后向散射光与仅由信号入射端一侧光纤反馈的大小基本一致.原因有两重: 一是输入光到达后端光纤时光强已经降低,产生的散射光强度较小;二是光纤本身存在吸收损耗,后端光纤中产生的后向散射光经过前端光纤后大大减弱,如果前端光纤损耗足够,这部分散射光甚至可以消耗殆尽.
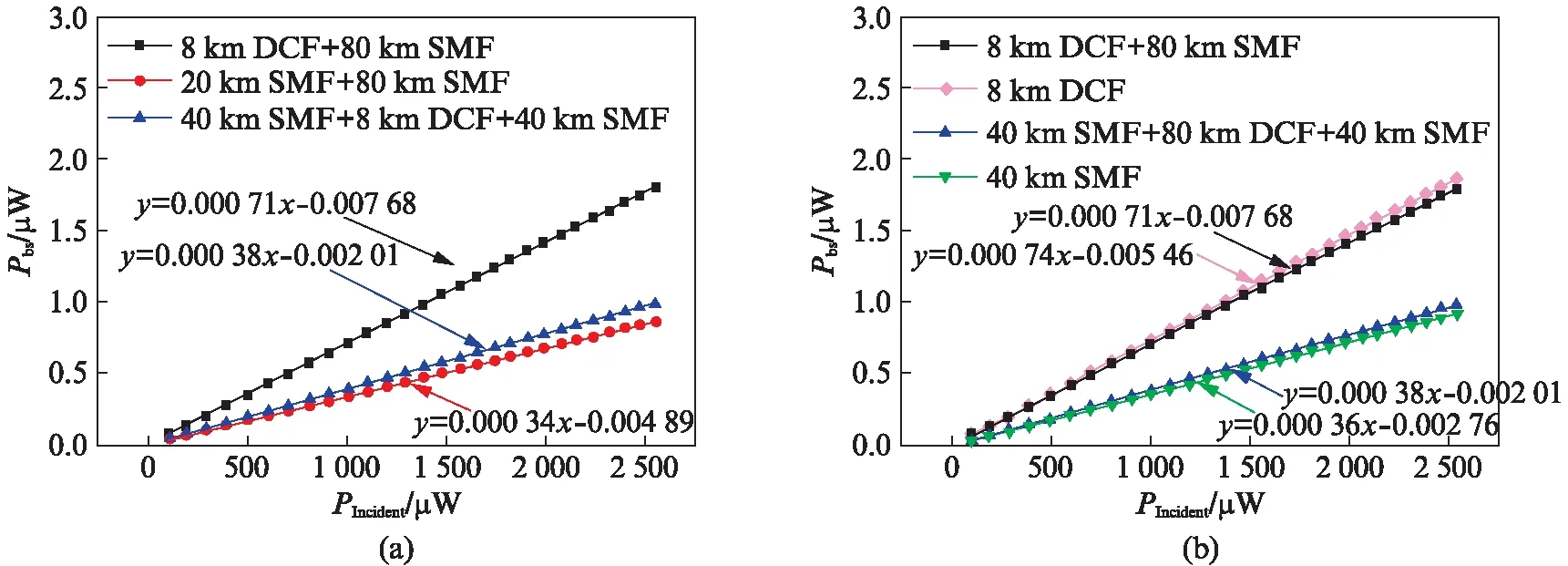
图4 后向散射光随入射光的变化曲线Fig.4 Back-scattered power as a function of the incident power
因此,对于图2(a)~(c) 3种情况,Pbs1和Pbs2主要由位于故Bi-EDFA信号输出端的光纤散射特性决定.由于位于Bi-EDFA1正向信号输出端的都是一段单模光纤,3种情况下Pbs1的大小一致.与图2(b)相比,图2(a)中位于Bi-EDFA2反向信号输出端的是一段8 km DCF,因此该情况下Pbs2应较大,系统输出端信噪比较差;而将DCF移至两段单模光纤中间后,图2(c)中Pbs2大小变为由单模光纤决定,系统信噪比应有所提升.


图5 基于LabVIEW的信号处理算法Fig.5 Block diagram of the data processing algorithm basedon LabVIEW
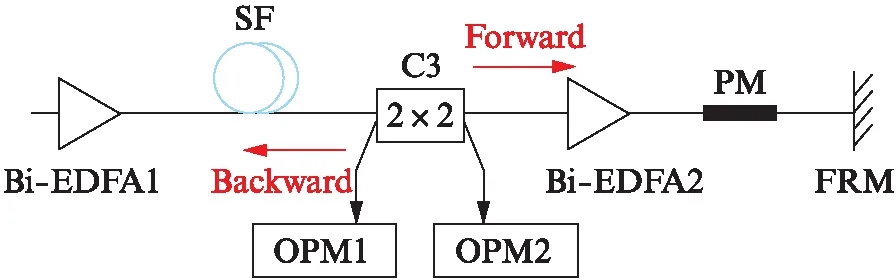
图6 散射光占比的计算方法Fig.6 Method to calculate the proportion of scattered power
图1(a)和(b) 2种情况下的散射光占比如图7(a)(见第478页)所示.可见与SMF-SMF(红线)情况相比,SMF-DCF(黑线)情况下的散射光占比较大,且两者间的差值随着泵浦电流的增加而增大.相同条件下,系统信噪比的对比结果如图7(b)所示,可见信噪比与散射光占比情况良好对应.综合图7(a)和(b)可以看出,由于SMF-DCF情况下散射噪声占比的增加,Bi-EDFA2的有效放大性受到更大抑制,系统信噪比始终低于SMF-SMF情况下的信噪比.因此,与单模线路中相比,带有色散补偿光纤线路中产生的散射光会对Bi-EDFA的工作状态造成更为严重的影响,系统信噪比明显降低,这是将色散补偿光纤用于传感线路色散补偿时存在的主要问题之一.
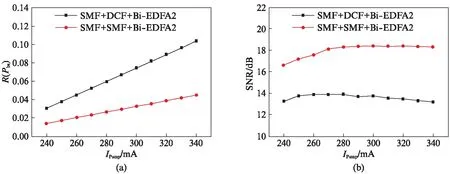
图7 带有色散补偿光纤线路和单模光纤线路的散射光占比和信噪比对比Fig.7 Comparison of the scattered power proportion and SNR between the two cases of SMF-DCF and SMF-SMF
3.2 系统信噪比提升方案分析
对于图1(a)和(c),即SMF-DCF和SMF-DCF-SMF 2种情况,为了详细分析不同信号光强度下改变DCF分布位置对系统信噪比的影响,调节Bi-EDFA1的泵浦电流,使得进入Bi-EDFA2的正向信号光功率分别为20、30、40、50 μW,其他器件的参数设置与第1组实验中保持一致.然后在每一种信号光强度下,以同样的方式调节Bi-EDFA2的泵浦电流并记录信噪比,同时利用耦合器C3计算出散射光在Bi-EDFA2入射光中所占的比例.
散射光占比的变化曲线如图8所示,图8(a)至(d)分别对应于20~50 μW不同信号光强度下的测试结果.可以看出,散射光占比与Bi-EDFA2泵浦电流成正比例关系,这是因为随着Bi-EDFA2泵浦电流的增加,反向光信号随之增强,传感光纤所反馈的后向散射光也随之增大.在上述几种信号光强度下,与SMF-DCF-Bi-EDFA2连接情况相比,将DCF位置调整到两段单模光纤中间后,散射光在Bi-EDFA2正向输入光中所占比例都有大幅减小,如图8中红线所示.这说明通过改变传感光纤中DCF的位置,可以有效抑制该线路反馈给Bi-EDFA2的后向散射噪声.
系统的信噪比的变化曲线如图9(见第480页)所示.对比图9与图8的测试结果可以看出,信噪比的变化趋势与散射光占比情况高度对应.当色散补偿光纤放置在2个单模光纤中间时,由于后向散射光占比的减少,Bi-EDFA2的有效放大性得到改善,系统信噪比同步提升;当Bi-EDFA2泵浦电流提升到一定程度后,由于Bi-EDFA2增益饱和,信噪比趋于稳定.但是对于SMF-DCF-Bi-EDFA2的连接情况,信噪比在曲线末端有所下降,这是因为散射光占比上升到很高的水平,超过了Bi-EDFA稳定工作的阈值.

图8 散射光在Bi-EDFA2入射光中所占比例Fig.8 The proportion of back-scattered power in the incident power of Bi-EDFA2
为了更直观地呈现SMF-DCF和SMF-DCF-SMF 2种分布情况间的信噪比差异(ΔSNR),将图9中红线和黑线的信噪比相减,并绘制出如图10(见第480页)所示的信噪比提升效果图.可见,将DCF位置调整到两段单模光纤之间后,随着Bi-EDFA2泵浦电流的增强,系统信噪比提升效果也越来越明显.图中存在几个波动点,这可能是因为散射噪声的增加使得Bi-EDFA2的工作状态趋于不稳定.当信号光强度为20 μW时,信噪比提升幅度最大,最大可达到3.5 dB.而随着光信号强度从20 μW逐步提升到50 μW,由于2种情况间散射光占比差距的缩小(如图8所示),信噪比整体的差异性也同步减小.综上,当传感线路中的DCF与Bi-EDFA直接相连时,该线路产生的散射光会严重影响Bi-EDFA的有效放大,甚至破坏Bi-EDFA的稳定工作点,导致系统信噪比恶化;而通过调整DCF分布位置,能够有效抑制进入Bi-EDFA中的后向散射噪声,提升系统信噪比,对解决该工程应用问题具有重要意义.
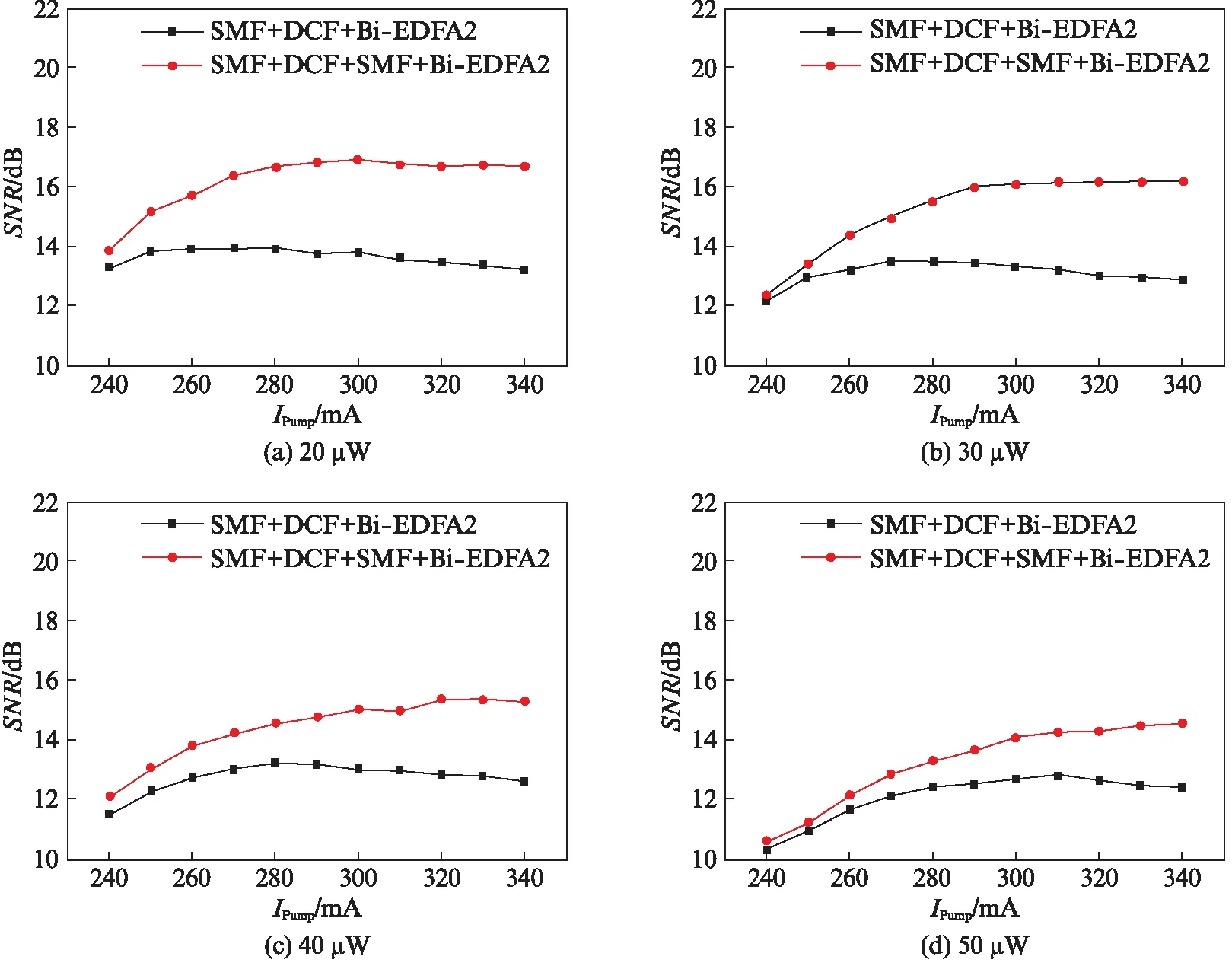
图9 两种DCF分布情况下的系统信噪比对比Fig.9 Comparison of the SNR in the two cases of different DCF distributions

图10 系统信噪比的提升效果Fig.10 Improvement of the system SNR
4 结 语
本文针对传感线路中的散射光,就其对基于Bi-EDFA的光纤传感系统信噪比的影响进行了详细研究.实验结果表明,线路反馈给Bi-EDFA的散射光强主要由与之直接相连的光纤散射特性决定,相同条件下DCF中产生的散射光强约为SMF中的2倍.因此,带有色散补偿光纤线路中产生的散射光对Bi-EDFA的有效放大限制程度更大.针对这一问题,通过将色散补偿光纤放置到2个单模光纤之间的简单方式,有效抑制了进入Bi-EDFA中的后向散射噪声,提升了系统信噪比.由于信噪比是影响系统灵敏度和精度的关键因素,本文研究可以为将基于Bi-EDFA的分布式光纤传感系统应用于长距离传感监测提供理论支持.
