随机波动格点方程的后向紧随机吸引子①

张子怡， 李扬荣

西南大学 数学与统计学院， 重庆 400715

文献[1-7]研究了吸引子的存在性以及吸引子的后向紧性并建立了相对完善的理论体系． 文献[8-10]研究了二阶格点方程的吸引子的存在性． 文献[11]以及文献[12]研究了带有非线性噪音的弱吸引子的存在性． 本文将在文献[11]的基础上， 研究带有乘法噪音的非自治随机波动格点方程的后向紧吸引子的存在性．

1 非自治随机动力系统的生成

(1)

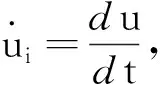
(A1)

hi(0)=0，α1≤h′i(s)≤α2

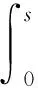
fi(s)s≥η1Fi(s)≥η2|s|2p+2

(2)

|fi(s)|≤η3(|s|2p+1+|s|)

(3)

(4)

(5)

(Bu)i=ui+1-ui， (B*u)i=ui-1-ui， (Au)i=-ui+1+2ui-ui-1， ∀u∈2

则有

(B*u，v)=(u，Bv)， (Au，v)=(Bu，Bv)， (Au，u)=(Bu，Bu)=‖Bu‖2≤4‖u‖2， ∀u∈2

(6)

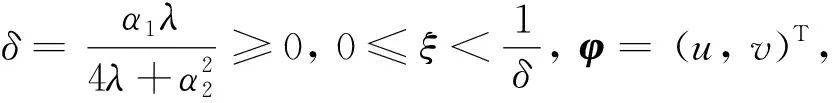
(7)

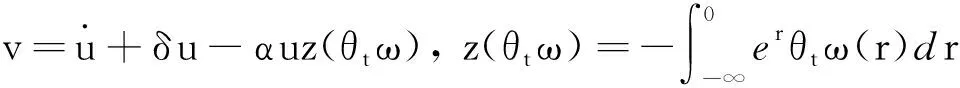
(8)

则方程(1)可转化为一阶随机微分方程

(9)

Φ(t，τ，ω，φ0)=φ(t+τ，τ，θ-τω，φ0)

可以验证Φ是一个非自治的随机动力系统， 即满足：

Φ(0，τ，ω， ·)=id，Φ(t+s，τ，ω， ·)=Φ(t，τ+s，θsω， ·)∘Φ(s，τ，ω， ·)

在下文中， 设D是X中所有后向缓增集构成的集族． 集合D∈D当且仅当

(10)

2 解的估计

引理1若假设(A1)，(A2)，(A3)成立， 则对任意后向缓增集D∈D， 任意的τ∈R，ω∈Ω， 存在T=T(D，τ，ω)≥1， 使得当φs-t∈D(s-t，θ-tω)时， 有

(11)

其中

证方程(9)可以等价地写为

(12)

其中

(13)

(14)

(15)

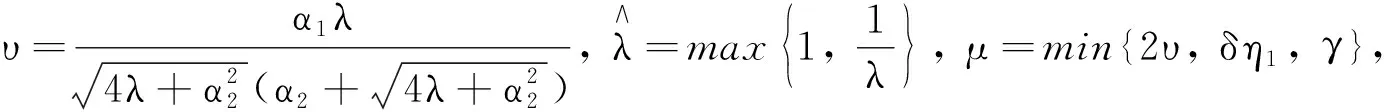
(16)

(17)

(18)

(19)

又令

将(17)-(19)式代入(16)式可得

(20)

对(20)式利用Gronwall不等式， 计算可得

(21)

由(2)，(3)式易证f(0)=0， ‖f(u)‖≤maxs∈[-‖u‖， ‖u‖]|f′(s)|‖u‖， 则有

(22)

(23)

对(21)式关于s∈(-∞，τ]取上确界， 结合(10)式可知， 存在T(D，s，ω)≥1使得当t≥T时， 有

(24)

因此(11)式得证， 即

(25)

推论1若假设(A1)，(A2)，(A3)成立， 由引理1， 方程(9)生成的非自治随机动力系统满足文献[3]， [13]中拉回后向一致吸收集存在的条件， 即协循环{Φ(t)}t≥0存在D-拉回后向一致吸收集K∈D， 其中

(26)

引理2若假设(A1)，(A2)，(A3)成立， 则对∀ε>0， (τ，ω， D)∈(R×Ω×D)，φs-t∈D(s-t，θ-tω)， 存在T(ε，τ，ω， D)>0，k(ε，τ，ω， D)≥1， 使得

(27)

(28)

易证

则有

其中C1，C2为常数， 将(29)-(31)式代入(28)式可知，

(32)

对(32)式运用Gronwall引理可得

(33)

由于φs-t∈D(s-t，θ-tω)(s≤τ)， 结合(10)式可得

(34)

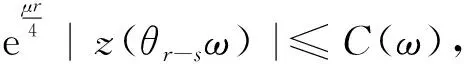
(35)

(36)

(37)

因此， 结合(23)式和(34)-(37)式可得， 对任意的ε>0， (τ，ω， D)∈(R×Ω×D)，φs-t∈D(s-t，θ-tω)， 存在T(ε，τ，ω， D)>0，k(ε，τ，ω， D)≥1， 使得

引理3若假设(A1)，(A2)，(A3)成立， 则协循环{Φ(t)}t≥0在吸收集K∈D上是后向渐近紧的．

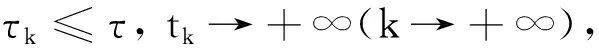
(38)

由引理1，φk在E中有界， 从而{(φk，i)|i|≤Nε}k在R2Nε+1中有界， 故{(φk，i)|i|≤Nε}k在R2Nε+1中有一个有限的ε-网， 结合(38)式可知{φk}在E中有一个有限的2ε-网， 从而{φk}在E中是预紧的， 即证得协循环{Φ(t)}t≥0在吸收集K上是后向渐近紧的．

3 后向紧随机吸引子

定义1一个非自治的随机紧集A∈D称为关于非自治协循环Φ的D-随机吸引子， 若

(i) A是不变的， 即Φ(t，τ，ω)A(τ，ω)=A(t+τ，θtω)，t>0；

(ii) A在hausdorff半距离意义下是吸收的， 即对任意D∈D，

定义2集合A={A(τ，ω)}称为后向紧的当A是紧的且∪s≤τA(s，ω)(τ∈R，ω∈Ω)是预紧的．

定理1若假设(A1)，(A2)，(A3)成立， 则方程(1)生成的动力系统存在后向紧随机吸引子．

证由文献[13](定理3.9)可知方程(9)生成的非自治随机动力系统Φ(t)存在唯一的后向紧D-拉回吸引子A∈D和唯一的可测D0-拉回吸引子A0∈D0． 再由文献[13](定理6.1)知A=A0， 故吸引子A也是随机的， 即Φ(t)存在唯一的后向紧D-拉回随机吸引子A∈D． 由文献[6， 15]可知方程(1)与方程(9)生成的随机动力系统共轭， 从而方程(1)存在后向紧随机吸引子．