可溶盐溶结循环对清水墙结构的风化影响

2021-10-22秦海洋汤永净2邵振东谷志旺陈智远

结构工程师 2021年4期

秦海洋汤永净2，，* 邵振东谷志旺陈智远

（1.同济大学土木工程学院地下建筑与工程系，上海200092；2.同济大学浙江学院土木工程系，嘉兴314051；3.上海仰韶古建筑保护科技发展有限公司，上海200434；4.上海建工四建集团有限公司，上海201103；5.上海市黄浦区教育局校产管理站，上海200025）

0 引言

截至目前，中国乃至世界建成有大量的清水砖建筑，这些建筑的寿命少则几年几十年，多则上百年，其结构或多或少的遭受了风化影响，水冻融循环与可溶盐溶结循环是导致墙体风化的主要因素［1-2］。其中，就上海、南京等南方城市而言，由于气温较高，水冻融的机会较少。因而周期性环境中干湿交替形成的可溶盐溶结循环成为南方地区清水墙结构风化的主要因素。

针对可溶盐对清水墙结构的风化机理，国内有不少学者对此展开了研究［3-4］。其中，汤永净和邵振东［5］通过对古砖砌体孔隙率和孔径分布的室内实验研究，认为孔隙率较大是导致整个风化过程的重要原因；范永丽等［6］通过X 荧光光谱与热力学软件HSC 等方法对砖体内部的物理及化学反应进行了观察与验证，指出可溶盐是导致清水墙破坏的主要因素；白宪臣等［8］对河南大学斋房建筑群古砖墙粉化脱落现象进行了分析，认为地下水分迁移、墙体的热湿状况及环境温度交替引起的可溶盐溶结循环是导致墙体风化的主要原因。上述成果极大推动了可溶盐对清水墙风化影响的研究进展，但却没有将冻融循环与溶结循环放在一起进行计算模型与计算结果的对比性分析，同时可溶盐溶结对清水墙的风化研究主要以实验研究为主，尚没有应用专业有限元软件对破坏机理做进一步验证，且截至目前尚没有系统化的专业软件可以直接模拟这一过程。鉴于此，本研究对比分析了水冻融循环与可溶盐溶结循环的作用特点与数学模型，并通过线性关系将二者联系起来，进而采用适用于水冻融循环分析的温度-应变耦合模型来近似模拟可溶盐溶结循环对清水墙结构的影响，进一步揭示出可溶盐溶结循环对清水墙风化影响的规律，以期为相应的理论分析和工程实践提供借鉴。

1 数学模型分析

1.1 对比性分析

水冻融循环与可溶盐溶结循环是导致清水墙结构风化的主要因素。其中，水冻融循环过程中，水冰相态的转变会导致结构体积的变化，进而产生应力累积；可溶盐溶结循环过程中，溶化与结晶相态的转变也会导致结构体积的变化，进而产生应力累积。由此可见，水冻融循环与可溶盐溶结循环具体破坏机理的相似性。截至目前，虽然无法直接模拟可溶盐溶结循环对清水墙结构的风化影响，但是基于“温度-应变耦合”模型的水冻融循环过程模拟已经十分成熟。因此，如果存在某对比研究方法可以证明冻融循环与可溶盐循环间存在联系，且可以通过数学关系表达出来，那么便可以采用发展较为成熟的冻融循环“温度-应变耦合”模型来近似模拟可溶盐溶结循环过程，深化研究可溶盐溶结循环对清水墙结构风化影响的客观规律，如图1所示。

图1 水冻融循环与可溶盐溶结循环的对比性分析Fig.1 Contrast analysis of freeze-thaw cycle and meltcrystallization cycle

1.2 相关性分析

1.2.1 条件假设

（1）零摄氏度为冻融循环的转化界线，临界含湿度为可溶盐的转化界线；

（2）溶结循环中，可溶盐始终处于饱和状态，假设可溶盐的结晶量变化与环境湿度变化线性相关。

1.2.2 数学模型

（1）冻融模型。温度T在0 ℃以下时，对于单位体积的冻融模型，温度每下降1 ℃，模型各边长延伸β，如图2所示。

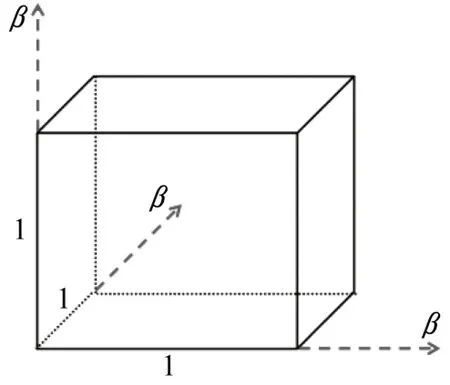
图2 单位冻融模型中的体积变化Fig.2 Volume change in freeze-thaw model

因而，单位体积增加量为：A=（1+β）3-1，其中，β为冻融模型的线膨胀系数。

（2）溶结模型。环境湿度低于临界含湿度α%时，对于单位体积的饱和溶结模型，其孔隙体积为1×φ。因而环境湿度c%每下降c%×1%，单位体积墙体结构中水分减少c%×1%×（1×φ）。假设可溶盐的溶解度为m%，则可析出可溶盐的量为c%×1%×（1×φ）×m%。因而可得B=cφm×10-6，如图3 所示。其中，c%为环境湿度，φ为溶结模型的孔隙比，m%为可溶盐的溶解度。

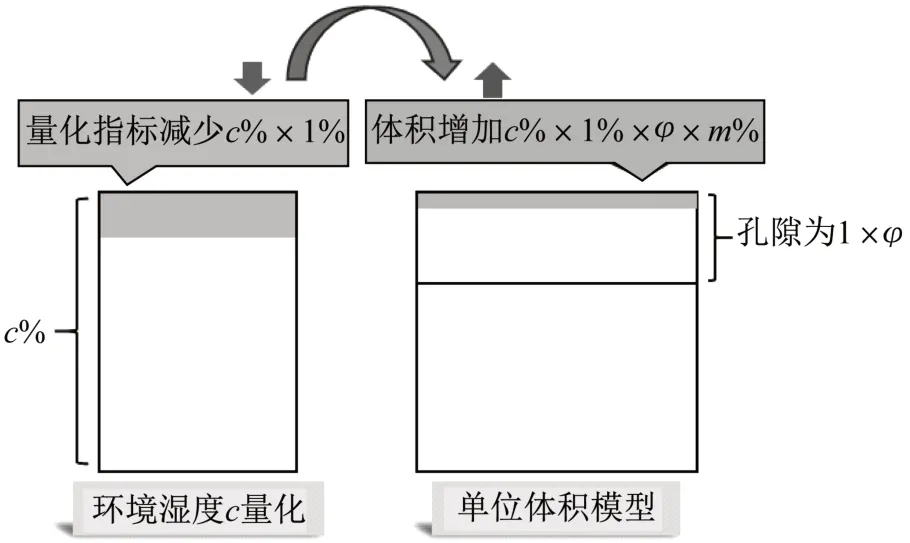
图3 单位溶结模型中的体积变化Fig.3 Volume change in melt-crystallization model

1.2.3 相关性分析

上述关于冻融模型和溶结模型的分析可知：冻融模型中，温度每降低1 ℃，单位体积增加量为A=（1+β）3-1；溶结模型中，环境湿度c%每降低原来的1%，单位体积结晶量增加B=cφm×10-6。因此可通过上述两式确定出体积增量相同时，可溶盐溶结循环与水冻融循环间的关系。即，溶结模型中，环境湿度c%每降低1%，对应于冻融模型中，温度将降低Al，其中

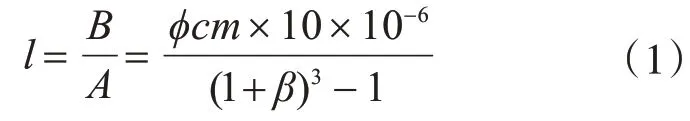
水冻融模型与可溶盐溶结模型存在破坏机理的相似性，且两者的控制因素环境温度T与环境湿度c%之间存在上述相关性，即B=Al。因此，可通过上述关系将溶结模型近似转化为冻融模型，进而通过“温度-应变耦合”模型方法进行可溶盐溶结循环过程的有限元分析，来探究溶结循环对南方清水墙风化影响的规律。

2 ABAQUS有限元模拟

以上海地区清水墙取样材料为例，并参考《砌体结构设计规范》等规范［10-12］，取线膨胀系数β为10-5/℃，孔隙比φ取值0.3，则由式（1）可确定出相关系数l，

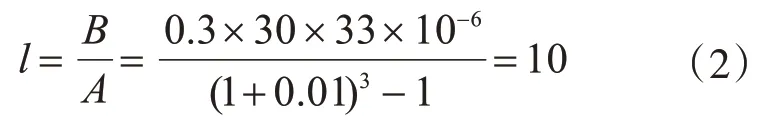
则温度-应变耦合模型中的温度变化幅值Al为10 ℃。

2.1 循环参数

基于“温度-应变耦合”方法的可溶盐溶结循环近似分析中，按上述结果取温度幅值为-10 ℃～10 ℃，每12 h 经历一次升温或降温的温度变化，即 24 h 经历一次可溶盐溶结循环［13］。以 10 次循环过程为例，总时长为240 h，温度变化曲线如图4所示。

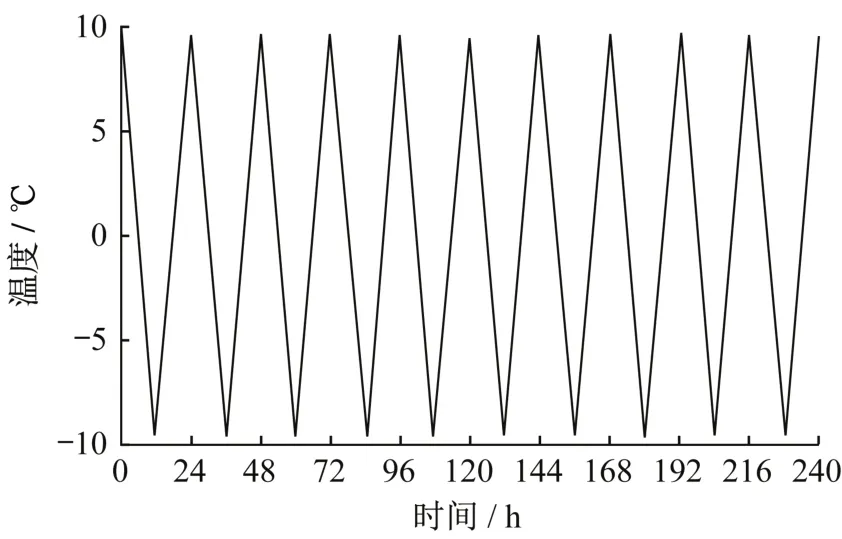
图4 温度变化曲线Fig.4 Temperature curve

2.2 模型参数

为了尽可能模拟清水墙的受力特征，模型尺寸取清水墙断面尺寸，长×高=300 mm×2 000 mm的二维平面模型，模型上下边界固定x与y方向的位移。在ABAQUS 6.14 版本中，设置步长为1 的固定分析步，总时长为240 h。整个模型的初始温度为幅值温度10 ℃，其右侧边界为清水墙外侧，设置为温度变化边界。模型尺寸及相关信息如图5所示。

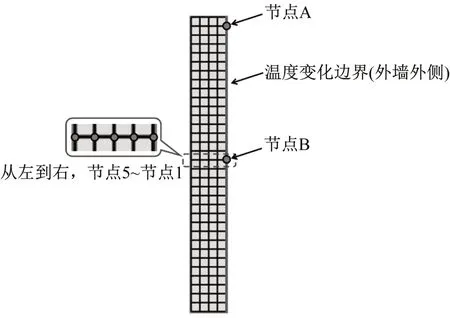
图5 计算模型Fig.5 The FEM model

导热系数、比热、热膨胀系数、杨氏模量及泊松比随温度的变化如表1所示。

表1 模型参数Table 1 Modek parameters

3 结果与分析

3.1 计算结果

图6 所示为溶结循环过程的不同时间点中，模型在x方向上的位移云图。

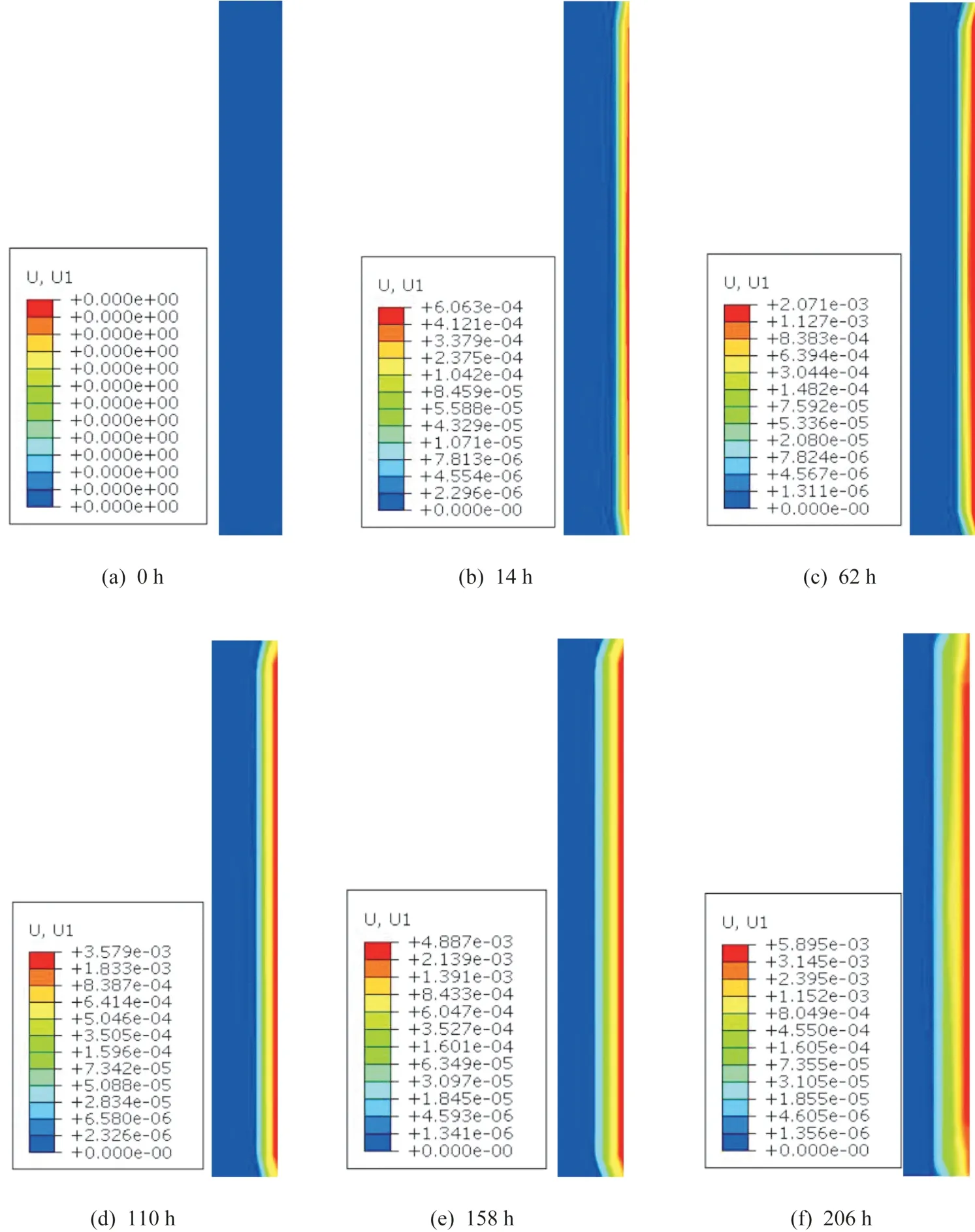
图6 溶结循环过程中的位移变化Fig.6 Displacement changes in the melt-crystallization cycle

3.2 节点位移的时间变化

提取图5 节点A 和节点B 在水平方向上随时间变化的节点位移，绘制成曲线图，如图7所示。

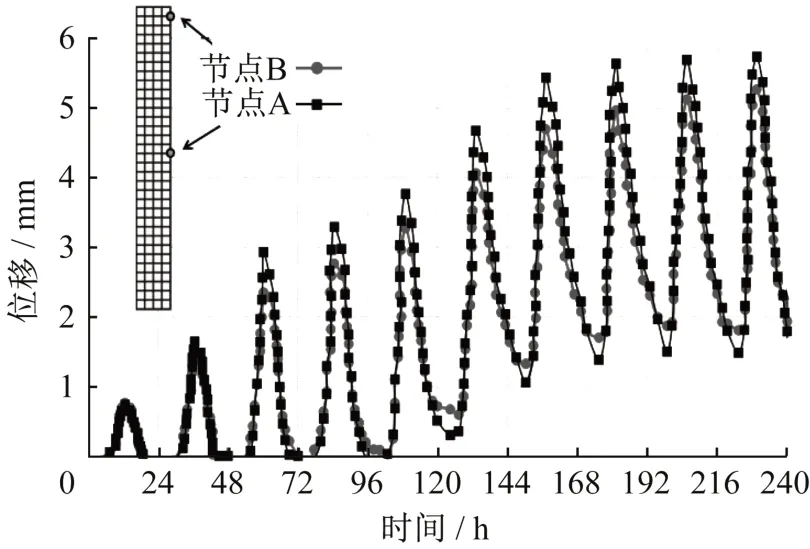
图7 节点位移时间变化曲线Fig.7 Displacement-time curve

可以发现，随着可溶盐溶结循环过程的进行，节点A 与节点B 的水平位移波动增大，且整体趋势为逐步趋于稳定，节点A 的最大水平位移为5.8 mm，节点B 的最大水平位移为5.4 mm。说明随着可溶盐溶结循环过程的进行，墙面泛碱现象中附带着墙体结构的部分风化，宏观上表现为墙面的向外膨胀，当膨胀发展到一定的程度最终趋于稳定。

就墙体外侧而言，中部膨胀较上下两端严重，部分原因是由于墙体的上下边界受限所导致的。实际工程中，墙体中部的泛碱和空鼓现象也常常大于上下两端［10］，这与上述计算结果表现相同。

3.3 节点位移的空间分布

提取14、62、110、158、206 小时模型中心节点（节点1～节点5）处的水平位移（图5 所示），绘制成曲线图，如图8所示。

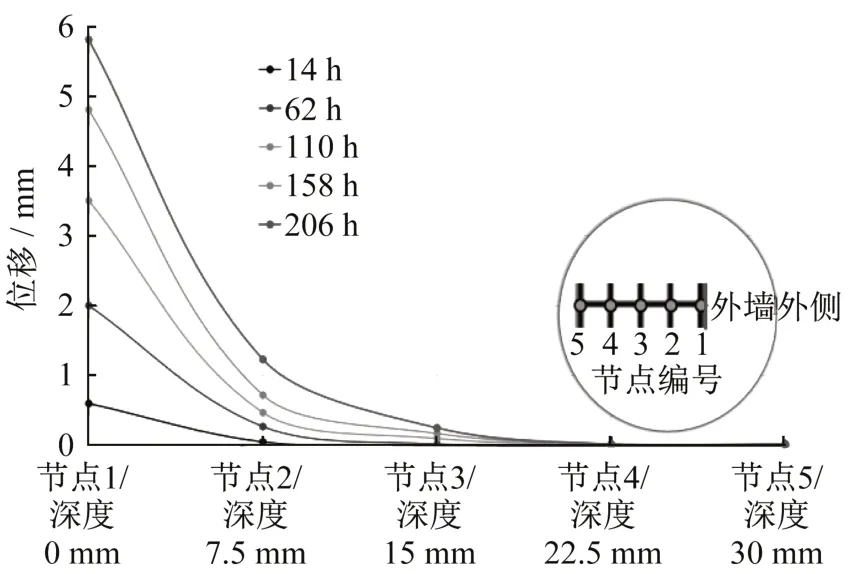
图8 节点位移空间分布曲线Fig.8 Displacement-space curve

可以发现，14 h 时（1 次溶结循环），只有墙体的外侧表面部分出现了水平位移，受影响区域厚度为7.5 mm，最大水平位移为0.6 mm，墙体内部基本无水平位移出现；62 h 时（3 次溶结循环），受影响区域稍微向墙体内部延伸，受影响区域厚度为10 mm，最大水平位移为2.0 mm；110 h 时（5 次溶结循环），受影响区域继续小范围向墙体内部延伸，受影响区域厚度为17 mm，最大水平位移为3.5 mm；158 h 时（7 次溶结循环），受影响区域为18 mm，最大水平位移为4.8 mm；206 h 时（9 次溶结循环），受影响区域仍为18 mm，最大水平位移为5.8 mm；

上述现象说明，可溶盐溶结引起的体积变化刚开始出现在外墙外侧，随着溶结循环次数的增加，逐步向墙体内部延伸，且延伸深度最终趋于稳定。当溶结循环达到9 次时，外墙外侧的水平位移明显大于内部水平位移，这对于清水墙的修缮工作具有重要的指导意义：周期小于9 年的清水墙修缮工程，计算结果可知，风化影响范围多涉及墙体表层而较轻地触及到墙体内部，因此高压水清洗表面的风化层，并进行墙体排盐施工后，便可极大程度地提高旧墙的质量。如果没有出现明显的结构问题，一般不需要进行额外的墙体加固。

4 讨论与分析

徐港等［14］通过实验发现，抗水冻融与抗盐冻融存在明显的线性关系，混凝土抗水冻融能力为抗盐冻融能力的2.5～2.8倍。

抗盐冻融实际上为水结冰的体积膨胀与可溶盐结晶的体积膨胀之和。本研究中的溶结模型不考虑水结冰时体积膨胀，仅分析干湿交替情况下可溶盐结晶时的体积膨胀。对比分析单一抗水冻融模型与单一抗盐冻融模型后，发现可以采用水冻融循环中的“温度-应变耦合”模型来近似模拟可溶盐溶结循环过程，两者间温度变化参数存在线性相关性且可以用文中的相关比例系数l=10来表示，该关系受多个因素的影响，孔隙比、环境湿度、可溶盐溶解度、线膨胀系数等因素。

深一步分析，本研究中的水冻融循环与盐析溶结循环组成的盐水结合体，直接叠加后的影响系数为11，其与水冻融循环的比值为11/10=1.1。因而在较多理想化假设的前提下，论文研究发现清水墙盐水冻融影响系数是纯水冻融影响系数的1.1 倍。该结果与文献［14］中的实验结论2.5～2.8倍具有较大的误差，该误差受较多因素影响，包括：①材料孔隙比、线膨胀系数等不同；②本研究中冻融模型与溶结模型过于简化；③水冻融循环模型与可溶盐溶结循环模型直接叠加会忽略两者的相互影响；④论文的三个假设、样本及其参数差异、理论与实验的差异等。

但是另一方面，论文的计算结果与文献［14］又具有高度的一致性，即抗水冻融与抗盐冻融存在明显的线性关系，这对于进行深一步的研究具有重要的参考价值。