单磁耦合式压电振动俘能器的建模与试验

2021-10-20张忠华柴君凌阚君武林仕杰王淑云黄乐帅

中国机械工程 2021年19期

张忠华柴君凌阚君武林仕杰王淑云黄乐帅

1.浙江师范大学精密机械与智能结构研究所，金华，3210042.浙江省城市轨道交通智能运维技术与装备重点实验室，金华，321004

0 引言

为满足无线传感设备、环境监测系统及定位装置等微功率设备的自供电需求，减少废弃化学电池带来的环境污染问题，秉持可持续发展的理念，基于电磁、静电及压电等原理的微型俘能器研究已成为国内外的热点[1-4]。其中压电振动俘能器具有结构简单、易微小化、输出能量密度大以及不易受天气影响等优势，故其适用范围更广，研究价值更高。悬臂梁式压电振动俘能器[5-10]因其结构简单而被广泛采用，但在实际环境中其振动频率及振幅变化范围大、不稳定，当激励频率远离压电振子固有频率时不宜被有效激励且振幅过大时易造成压电振子损毁，因此提高俘能器的频率适应性、有效带宽以及可靠性是提高其实用性的前提[11]。

目前，用来提高俘能器频率适应性及频带宽度的方式主要分为三类：①预加轴向力式[12]，在简支梁两端施加轴向预压力，可实现俘能器在单、双稳态间切换从而拓宽频带，其主要弊端是需要增加额外的机械配件；②撞击式[13]，通过设置刚性或弹性挡块使俘能器具有多段刚度，从而实现拓频，但会产生较大的噪声，且撞击易使装置损坏；③磁耦合式[14-16]，引入磁力使系统具有两个或多个稳态，使其在较宽频带下更易实现大幅阱间振动，可有效提高环境适应性，但现有的磁耦合式压电振动俘能器结构中的压电陶瓷都被直接粘在梁上，工作中受到交替的拉压应力，而压电陶瓷受拉易产生裂纹，因此可靠性较低，尤其不适于应用在外界振幅、噪声等变化较大的环境中[17]。

本文提出的单磁耦合式压电振动俘能器通过辅助梁激励预弯的压电振子来构成组合换能器，实现了压电振子的单向激励，解决了压电振子在工作中承受交替拉压应力易碎裂的问题，同时利用磁耦合调节俘能器的固有频率和有效带宽，从而提高其环境适应性。

1 俘能器结构及原理

单磁耦合式压电振动俘能器结构如图1所示，主要由一对压电振子、辅助梁、动磁铁、定磁铁和框架等构成。由铜基板和压电片组成的压电振子对称安装于辅助梁两侧并施加一定的预压力，动磁铁设在辅助梁自由端，定磁铁安装于框架上。由图1可知，当磁铁的间距、角度、重力以及磁力等系统参数的组合不同时，俘能器的性能会有很大的差异，可通过调节上述参数的大小来调整俘能器的性能。

图1 俘能器装置结构示意图Fig.1 Structure diagram of energy harvester system

在实际工作过程中，该方案的压电振子仅受到单向的压应力。当辅助梁向上摆动时，安装于辅助梁上侧的压电振子受激开始远离中心平衡位置；当辅助梁向下摆动时，上侧压电振子在自身弹性力的作用下弹回平衡位置。基于此，在保证压电振子与辅助梁不分离的情况下，压电振子仅受到辅助梁的压应力，以提高俘能器的可靠性。

本文主要通过改变定磁铁的位置(图1中磁铁水平耦合距离d和竖直耦合距离h)和角度(图1中耦合角α)来改变磁力的大小，进而改变俘能器的幅频特性。通过改变磁铁竖直耦合距离以及耦合角能够给动磁铁施加磁悬浮力，进而降低动磁铁重力对俘能器的影响，提高其发电性能。

本文还通过COMSOL仿真及试验来研究磁铁水平耦合距离、竖直耦合距离及耦合角对磁铁磁力、系统势能及俘能器输出性能的影响，从而验证单磁耦合式压电振动俘能器原理的可行性。

2 模型建立与有限元仿真分析

由俘能器的结构和工作原理可知，当压电振子的固有频率高于辅助梁的固有频率时，压电振子受激励后反向回弹过程中其自由端不会与辅助梁脱开，故其最大形变量是由辅助梁决定的，控制辅助梁的振动状态就间接地控制了压电振子的振动状态。为便于分析，将辅助梁视为受弹性力、磁耦合力、重力、阻尼力及机电耦合力作用的弹簧-质量-阻尼模型，如图2所示。模型参数Meq、ceq、Keq分别为等效质量、等效阻尼和等效刚度，Zm、Zn分别为磁铁的纵向位移和外界激励位移，R为外接负载电阻。

图2 俘能器的集总参数模型Fig.2 Lumped parameter model of energy harvester system

根据牛顿第二定律和基尔霍夫定律，俘能器的动力学方程为[18]

(1)

式中，Fp为等效质量所受的机电耦合力；Cp为压电片的等效电容；U为R两端的电压；αc为机电耦合系数；Z为等效质量的相对位移，Z=Zm-Zn；Fv为动磁铁所受磁力在竖直方向的分量；A为外界激励振幅；ω为外界激励角频率；t为时间。

根据欧拉-伯努利梁理论，等效刚度Keq可以表示为

Keq=K1+K2=(1+λ)K1

(2)

式中，K1、K2分别为辅助梁和两个压电振子的等效刚度；λ为比例系数；E为辅助梁的弹性模量；l为等效梁长；lb、lm分别为辅助梁和磁铁的长度；I为辅助梁的惯性矩；wb、hb分别为辅助梁的宽度和厚度。

磁力大小由磁铁间距和角度决定，磁力Fm变化时，俘能器的动力学特性及幅频特性会发生很大的变化。单磁耦合结构中磁铁间的关系如图3所示，动磁铁振动幅度远小于辅助梁长度，故将其运动轨迹简化为竖直上下运动。集总参数模型中两磁铁的尺寸相同，假定d、h、α分别为初始时刻下磁铁的水平耦合距离、竖直耦合距离及耦合角，Zm为某一时刻下动磁铁的纵向位移，ma、mb分别为磁铁a和磁铁b的磁矩，rab为磁铁a到磁铁b的方向向量。

图3 单磁耦合下磁铁相对位置示意图Fig.3 Schematic diagram of the magnet’s relative position under single-magnet coupled

以水平耦合距离d=10 mm、竖直耦合距离h=6 mm、耦合角α=10°为例，磁铁纵向位移和磁力竖直分量关系的仿真曲线和拟合函数曲线见图4。图4中曲线表明拟合函数曲线与仿真曲线的变化趋势基本一致，其残差模仅为0.4，拟合函数的表达式如下：

Fv=-0.06u9+0.28u8+0.36u7-2u6-0.42u5+

5.1u4-0.9u3-4.9u2+1.7u+0.98

(3)

图4 磁铁纵向位移和磁力竖直分量的关系曲线Fig.4 Relationship curve between longitudinal displacement of magnet and vertical component of magnetic force

磁力大小由磁铁间距和角度等要素决定，由式(1)可知磁力的变化直接影响俘能器的动力学特性，可通过势能来解释磁力对俘能器性能的影响。本文利用有限元仿真的方法来研究各参数对系统势能的影响，仿真所用的参数见表1。

表1 仿真用相关参数Tab.1 Related parameters for simulation

考虑重力、弹性及磁势能时，俘能器的势能可表示为[19]

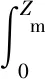
(4)

图5a给出了竖直耦合距离h=0、耦合角α=0°、水平耦合距离d不同时，势能Ep与动磁铁纵向位移Zm的关系曲线。由图5a可知：当d=24 mm时，势能曲线为单势阱，d减小到14 mm时，由单势阱变为双势阱，原点处变为一个非稳定平衡位置，由于重力影响，双势阱不完全关于原点对称。双势阱间的跨度随d减小而增大，各自的阱深随d减小而加深，当d<10 mm时，阱深随d减小而大幅加深。由于过深的势阱不利于拓宽频带，因此研究h及α对势能的影响时，选择的d介于10～14 mm之间。图5b给出了d=11 mm、α=0°及h不同时，U与Zm的关系曲线。由图5b可知：随h增大，曲线由对称转变为非对称，直至h增大至10 mm时，非对称的双势阱变为单势阱。图5c给出了d=14 mm、h=6 mm及α不同时，U与Zm的关系曲线。由图5c可知：随α增大，曲线的非对称度先减小后增大(即其中一个阱深不断加深，而另一个阱深不断变浅)，存在较佳耦合角(α=60°)使得势能曲线趋于对称双势阱。

(a)d不同时势能与动磁铁纵向位移的关系曲线

仿真结果表明：通过改变磁铁水平耦合距离、竖直耦合距离以及耦合角能够调节俘能器的动态性能。

3 试验测试与分析

为验证单磁耦合式压电振动俘能器原理的可行性，并获得系统参数对俘能器输出性能的影响规律，设计制作了图6所示的试验样机和测试系统。测试系统设备主要由DC-1000振动台、SA-15功率放大器、RC-2000振动控制仪、俘能器及数字示波器等组成。试验所用器件及参数与仿真时相同，其中预弯压电振子的长、宽、厚、预弯半径分别为40 mm、40 mm、0.5 mm、140 mm，激励磁铁被安装在设有角度盘的夹具上，通过夹具可灵活调节磁铁的位置和角度。试验施加振幅为1.5 mm、频率为10～35 Hz的正弦激励信号，试验发现上下侧压电振子的幅频特性基本一致，这里选取上侧压电振子开路电压的峰峰值Ug来表征俘能器的输出性能。

图6 俘能器测试系统Fig.6 Testing platform of energy harvester system

图7为竖直耦合距离h=0、耦合角α=0°、水平耦合距离d不同时俘能器的幅频特性曲线，其中d=∞即为无磁耦合(non-magnetic coupling,NMC)情况。由图7可知：d=11 mm时曲线较为平坦，d=10 mm时存在两个峰值，其余幅频特性曲线只有一个峰值，通过调节水平耦合距离得到的俘能器固有频率和有效频带(电压峰峰值在10 V以上)的调节范围分别为13～29 Hz和12.7～30 Hz。当d≤10 mm时，随d减小，固有频率提高、有效带宽变宽，且变化明显；当d≥13 mm时，随d增大，固有频率缓慢提高、有效带宽缓慢变宽；当d=11 mm时固有频率为13 Hz，有效频带为12.7～28.7 Hz，最大电压峰峰值为15.4 V，该条件下的曲线平缓，且固有频率较低、有效频带较宽，提高了俘能器的可靠性和环境适应性。d太小时俘能器会出现势能壁垒，从而导致俘能器的发电性能降低，d过大时耦合磁力会大幅减小，这与理论分析相吻合。试验结果表明，磁铁水平耦合距离对俘能器发电性能有较大的影响，因此在实际工作中需根据振动情况选择较佳的水平耦合距离。

图7 水平耦合距离不同时的幅频特性曲线Fig.7 Amplitude-frequency characteristic curve under different horizontal coupling distances

图8为水平耦合距离d=11 mm、耦合角α=0°、竖直耦合距离h不同时俘能器的幅频特性曲线，其中h=∞即为无磁耦合情况。由图8可知：h=0时曲线较为平坦，h=1 mm时存在两个峰值，其余幅频特性曲线都只出现了一个峰值，且随h增大，峰值向后推移。通过改变h得到的俘能器固有频率的调节范围为13～27 Hz；固有频率和有效频带的最低频率均随h增大而提高，且提高的速度逐渐减缓；有效带宽受h的影响较小，且始终稳定在15.2 Hz附近。相较于无磁耦合情况，当h≤2 mm时，磁耦合式俘能器增加了低频响应，当h≥4 mm时，该俘能器增加了高频响应。在h增大过程中动磁铁受非对称单势阱的影响，其摆动幅度会减小，进而会降低俘能器的发电性能，这与理论分析相吻合。因此，在保证磁力能够抵消动磁铁重力的条件下，应尽可能地减小磁铁的竖直耦合距离。

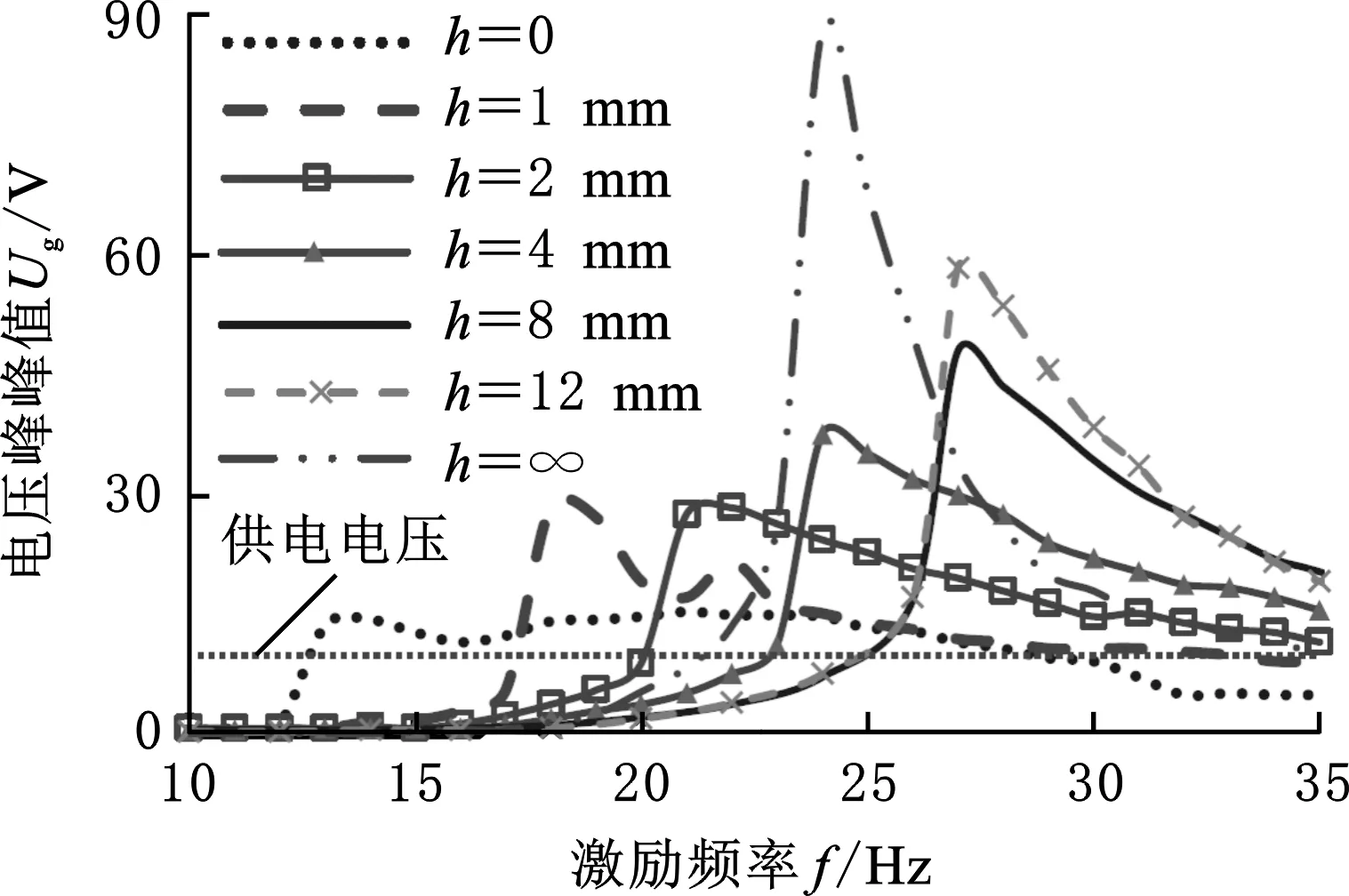
图8 竖直耦合距离不同时的幅频特性曲线Fig.8 Amplitude-frequency characteristic curve under different vertical coupling distances

图9为d=14 mm、h=6 mm、α不同时俘能器的幅频特性曲线。由图9可知：耦合角较大或较小时幅频特性曲线均只出现一个峰值，仅当α=67.5°时，曲线较为平坦。通过调节α得到的俘能器固有频率和有效频带的调节范围分别为16～23 Hz和15.4～35 Hz。存在较佳耦合角α=67.5°使俘能器固有频率降低至16 Hz，最大电压峰峰值减小至22.8 V，有效带宽拓宽至19.6 Hz，较无磁耦合条件下的有效带宽13.6 Hz拓宽了6 Hz，α=67.5°条件下的曲线非常平缓，既拓宽了频带又提高了可靠性，与仿真得出的较佳耦合角的差值仅为7.5°，此外，该条件下动磁铁重力被耦合磁力抵消，优化了俘能器的发电性能。因此，在实际环境中应用该俘能器时，可通过调节耦合参数，使其达到较佳的发电性能。

图9 耦合角不同时的幅频特性曲线Fig.9 Amplitude-frequency characteristic curve with different coupling angles

为了进一步优化俘能器的输出性能，研究了不同激励频率下负载电阻对输出功率的影响规律。图10给出了水平耦合距离d=12 mm、竖直耦合距离h=0、耦合角α=0°、激励振幅为4.5 mm、激励频率f不同时输出功率Pg与负载电阻R的关系曲线。由图10中曲线可以看出，每个激励频率均对应有一个较佳负载电阻可使装置的输出功率最大，且频率变化对较佳负载电阻的影响不大，负载电阻均在70 kΩ左右；激励频率对输出功率的影响较大，当激励频率分别为12 Hz、16 Hz、20 Hz时，最大输出功率分别为5.27 mW、2.96 mW和1 mW。试验发现，激励位置h、d与角度α不变时，通过调节负载电阻使其与俘能器阻抗相匹配，从而可提高俘能器的功率输出。