Mo掺杂调控钛酸铋钠铁电陶瓷带隙的实验与第一性原理研究
2021-10-19谢晓宇黎清宁周昌荣胡朝浩袁昌来许积文
谢晓宇,黎清宁,周昌荣,2,胡朝浩,2,袁昌来,2,许积文,2
(1.桂林电子科技大学材料科学与工程学院,桂林 541004;2.桂林电子科技大学,广西信息材料重点实验室,桂林 541004)
0 引 言
随着环保意识的提高,人们迫切希望解决日益增长的能源需求与传统化石能源产生碳排放污染之间的矛盾,太阳能被认为是有前景之一的清洁能源[1],如何提高材料对太阳光吸收引起众多研究者关注[2]。具有自发极化特点的铁电材料,由于所产生的铁电光伏效应跟传统p-n结的光伏响应不同,在光吸收应用中表现出很好的潜力[3],故研究人员一直在尝试通过各种途径改善铁电半导体材料的光学性能,其中离子掺杂调控是一种简单有效的方法[4]。
Na0.5Bi0.5TiO3(BNT)基无铅陶瓷是一种绿色ABO3型钙钛矿铁电材料,具有一定的光吸收能力,但纯BNT光学带隙较高(3~3.2 eV)[5],故希望通过离子掺杂调控改善其光吸收强度,降低光学带隙,提高光吸收强度。Gebhardt等[6]研究发现过渡族阳离子会占据B位,导致氧八面体中心偏离,造成畸变,改变钙钛矿陶瓷的光学带隙。Pham等[7]研究发现,通过掺杂Mo可以使 NiTiO3陶瓷光吸收强度增加,从而减小光学带隙值。Liu等[8]通过第一性原理计算研究发现,掺杂Mo可以改善SrTiO3光吸收波长范围。Khan等[9]、Yu等[10]通过理论计算研究发现,掺杂Mo可减小TiO2带隙,为n型掺杂。但目前对通过Mo掺杂BNT基无铅铁电陶瓷进行带隙调控的研究较少,其对带隙的影响规律与机理有待深入研究,本文通过掺杂不同成分的Mo研究了BNT基陶瓷的光吸收和光学带隙的变化,通过第一性原理计算分析了掺杂体系带隙变化的机理。
1 实验与计算方法
1.1 样品制备与表征
采用分析纯的原料Bi2O3、Na2CO3、TiO2和MoO3,其纯度均大于99%(质量分数),根据Na0.5Bi0.5(Ti1-xMox)O3(BNT-Mox,x=0%,0.5%,1.0%,1.5%,2.0%)准确称量配料后,以无水乙醇为球磨介质球磨24 h后置于80 ℃烘干,采用两步过筛法处理粉料。第一步过筛使用100目(160 μm)的筛网,将烘干后的粉料通过筛网过滤,然后将过滤后的粉料放入预烧炉,在850 ℃预烧环境下保温2 h,将预烧完成的粉料破碎后加入7%的PVA黏结剂适量,搅拌均匀后再次烘干,重新研磨成粉料。第二步过筛使用150目(100 μm)的筛网,将研磨后的粉料过滤。粉料经过两步过筛后,称取适量粉料放入压片模具进行压制成型,在10 MPa压力下将粉料压制成直径19.5 mm、厚1.2 mm左右的圆坯。将坯料置于马弗炉中慢速升温至600 ℃后保温2 h排胶,然后升温至1 120 ℃保温3 h。由于烧制过程中会造成Na和Bi的挥发,故采用埋烧法将原粉料覆盖在样品表面后烧制,以减少样品损失。
测试使用德国Bruker D8-2-Advance型号的X射线衍射仪表征陶瓷样品的晶体结构,测试采用Cu靶,Kα射线,测试范围为20°~80°,步长为0.02°,扫描速度为8 (°)/min。采用法国HORIBA LabRAM HR Evolution高分辨显微共焦拉曼光谱仪研究样品的价键振动变化,室温下采用Ar 532 nm离子激光,设置测试范围为40~1 000 cm-1,单次采谱时间为5 s,循环次数为2,实时采集曝光时间为2 s。使用美国PerkinElemer Lamber750S紫外-可见-近红外分光光度计研究样品的光吸收,测量波长范围为200~1 000 nm,间隔点设置为5 nm。
1.2 模型构建与计算方法
室温下BNT属于三方相[11],三方相BNT空间群为R3c,如图1(a)所示。晶格常数a=b=c=0.55 nm,α=β=γ=59.80°[12],使用VESTA(visualization for electronic and structural analysis)[13]建立2×2×2超晶胞,采用原子替代的掺杂方法,用Mo替代Ti原子[14],如图1(b)所示。

图1 (a)空间群为R3c的纯BNT;(b)BNT的2×2×2超晶胞掺MoFig.1 (a) Pure BNT in R3c space group of rhombohedral; (b) Mo doped BNT 2×2×2 super cell
计算使用VASP软件包(the viennaAbinitiosimulation package)[15-17]对模型进行结构优化和计算。计算采用的交换关联泛函为局域密度近似(local-density approximation, LDA)[18],采用的赝势方法为投影缀加平面波赝势(PAW)方法[19-20]。计算考虑的价电子为Bi:5d106s26p3、Na:2p63s1、Ti:3p63d24s2、O:2s22p4、Mo:4d55s1。由于计算中含有过渡族金属元素,而过渡族金属元素的电子间库伦相互作用不可忽略,为强关联电子体系,故采用在位库伦修正的方法(on-site coulomb correction),即LDA+U计算法(Ti:Ueff=U-J=5.8 eV;Mo:Ueff=U-J=2 eV)[14]。计算使用Monkhorst-Pack方法设置k点网格为4×4×4,设置平面截断能Ecut=500 eV,原子间相互作用力不大于0.2 eV/nm,能量收敛精度为1×10-5eV。
2 结果与讨论
图2为BNT-Mox陶瓷的XRD谱。由图2(a)可看出,所有样品均为钙钛矿结构且无明显杂峰。从图2(b)看出随着Mo掺杂量的增加,在40.4°处的(210)峰,峰宽变窄,46.9°处(220)峰的峰宽和峰强有劈裂变化,样品掺杂前后从三方相转变到伪立方相[21]。

图2 BNT-Mox陶瓷的XRD谱Fig.2 XRD patterns of BNT-Mox ceramics
图3为室温下BNT-Mox陶瓷的拉曼散射光谱,与已报道的BNT基陶瓷拉曼光谱类似[5,22]。其各个峰的位置分别位于56 cm-1、123 cm-1、274 cm-1、517 cm-1、581 cm-1和768 cm-1,其中40~200 cm-1是对应A位阳离子变化有关的范围[23];200~450 cm-1是对应Ti—O键变化有关的范围;450~700 cm-1是对应B位氧八面体变化有关的范围。700 cm-1以后是对应A1(longitudinal optics, LO)与E(LO)两种模式重叠的范围[24-26],在768 cm-1附近为受TiO6八面体团簇扭转位置影响的LO3模式[27-29]。可以看出,随着掺杂量的增加,在274 cm-1和517 cm-1处峰强增大,表明Mo掺杂影响了Ti—O键与TiO6八面体,进入了B位。

图3 BNT-Mox拉曼散射光谱Fig.3 Raman spectra of BNT-Mox
图4(a)为BNT-Mox的紫外-可见-近红外光谱法测定的吸收光谱,其测量波长范围为200~1 000 nm。可看出样品的光吸收主要集中在300~400 nm波长范围内,Mo掺杂后吸收强度有显著提升,且当x=1.0%时吸收强度最大值为69%。光吸收强度与光学带隙之间有相关性,Huang等[30]认为带隙减小是因为Mo离子掺杂影响Ti离子轨道导致的。图4(b)为样品光学带隙随掺杂成分的变化,可由Kubelka-Munk函数曲线的切线在横坐标上的截距得出[31]。可看出随着掺杂量的增加,光学带隙先减小再增大,当x=1.0%时达到最小值2.33 eV,随后增大至2.46 eV。
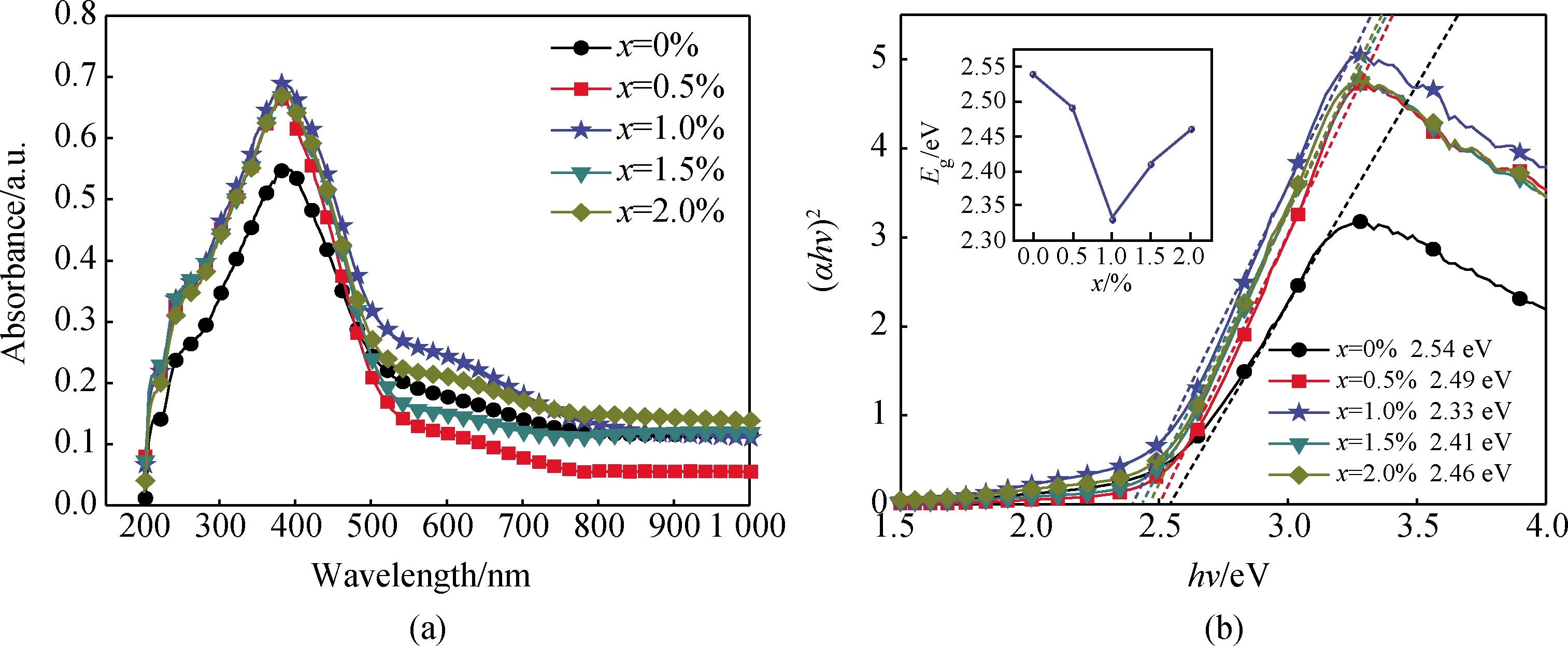
图4 (a)掺杂量对BNT-Mox陶瓷的光吸收谱的影响;(b)掺杂量对 BNT-Mox陶瓷光学带隙图影响Fig.4 (a) Influence of compositions on optical absorption spectrum of BNT-Mox ceramics; (b) influence of compositions on optical band gap of BNT-Mox ceramics
为了进一步研究Mo掺杂BNT可以增强光吸收和调控光学带隙的机理,利用VASP和VASPKIT后处理软件包,结合VESTA等建模软件[13,17],建立纯BNT与Mo掺杂BNT的模型,并分别计算和处理得出二者的能带结构与总/分态密度图。图5(a)为纯BNT的能带结构图,其中能带的路径和高对称点由Seekpath等[32]以及Setyawa等[33]研究得出。高对称点处的竖线表示该点有不同的路径。由图5(a)可看出,价带顶位于Γ点处,导带底位于T点处,为间接带隙,与周树兰等[34]结论趋势一致。图5(b)为BNT-Mox的投影能带图,其中红色竖线标记为Mo元素投影,标记越大表示所占权重越大,可以看出Mo掺杂主要对体系的导带产生影响。Mo掺杂后相对于纯BNT导带降低,且在费米能级处有能带穿过,表明在掺杂体系禁带内有杂质能级[10,35]。导带底与价带顶在同一Γ点处,为直接带隙。

图5 (a)纯BNT能带结构图;(b)Mo掺杂BNT能带结构图Fig.5 (a) Band-structure of pure BNT; (b) band-structure of Mo doped BNT
图6(a)为纯BNT的总态密度(TDOS)与各元素分波态密度(PDOS)图,可得价带的主要贡献为O 2p轨道,导带的主要贡献为Ti 3d轨道。由图6(b)态密度图可知,掺杂体系内的杂质能级主要由Mo 4d轨道贡献,费米能级处的导带主要由Mo 4d、Ti 3d与Bi 6p轨道杂化形成,价带主要贡献为O 2p轨道。综上可知:当Mo掺杂量低时,能带结构由间接带隙转变为直接带隙,引入的杂质能级起主导作用,导致本征带隙减小;随着Mo掺杂量进一步增加,由于费米能级进入导带中,导带底的能量状态被占据,导带内电子占据态将费米能级推向更高的能量,掺杂量高时莫斯-布尔斯坦[36-37]效应起到主导作用,可引发表观光学带隙增加[38-39];这两种带隙调控机制相互竞争,其主导作用随Mo掺杂量增加而改变,从而导致光学带隙先减小后增大。
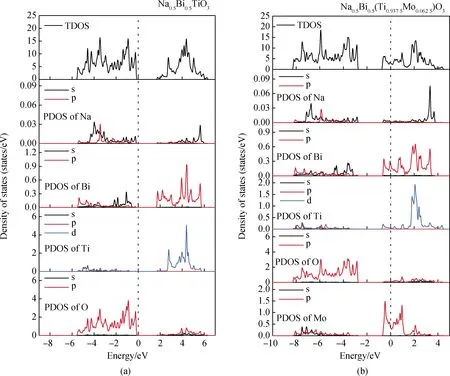
图6 (a)纯BNT的TDOS与PDOS图;(b)Mo掺杂BNT的TDOS与PDOS图Fig.6 (a) TDOS and PDOS of pure BNT; (b) TDOS and PDOS of Mo doped BNT
3 结 论
(1)本文采用传统固相法合成了BNT-Mox陶瓷,XRD和拉曼光谱表明BNT陶瓷掺杂过程中发生从三方相到伪立方相的转变。
(2)随着Mo掺杂量的增加,光学带隙先减小后增大,在Mo掺杂量为x=1.0%时,光吸收强度达到最大值,光学带隙值达到最小值2.33 eV。
(3)通过理论计算分析,Mo掺杂BNT导致体系禁带内有杂质能级,杂质能级主要由Mo 4d轨道贡献,导致能带结构由间接带隙转变为直接带隙,本征带隙减小。Mo掺杂导致的杂质能级与莫斯-布尔斯坦效应之间存在带隙调控相互竞争关系,可有效调控BNT体系能带结构。
