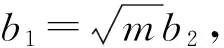薄壁圆管膨胀变形行为的量纲分析及理论研究

吴明泽，张晓伟，钟贤哲，张庆明

(北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

提 要:通过有限元数值方法及已有圆管膨胀试验对金属圆管膨胀的变形行为进行研究，研究发现圆管膨胀后的几何尺寸h和D1主要受圆管和压模初始几何结构参数影响，而受圆管材料和摩擦因数的影响较小；基于量纲分析，得到膨胀后圆管的几何尺寸h和D1与主要影响因素之间的量纲一关系式. 结合量纲一关系式与能量守恒定律，提出圆管稳态膨胀过程中稳态下压力的预测模型，模型中考虑了材料的应变强化效应和压模外径对膨胀管弯曲区域曲率的影响，结果表明该模型的预测值与试验结果、仿真结果能较好地吻合.

薄壁结构具有较高的比强度和比刚度，而且在受到冲击载荷作用时表现出良好的吸能特性. 因此，在抗冲击结构中得到广泛的应用[1-3]，如列车车厢之间的防冲击碰撞保护装置[4]. 其中，薄壁圆管的膨胀变形具有变形过程稳定、载荷平稳、对下压载荷方向不敏感等特点，而引起学者广泛关注[5]. 相关研究表明膨胀管的吸能性能不仅受圆管和压模的几何结构影响，同时圆管与压模接触表面的摩擦因数和冲击速度对此也有较大的影响[6-8]. 其中，膨胀稳态力作为反映圆管变形吸能性能的重要指标，对其建立相关的预测模型，将对膨胀管吸能装置的结构设计具有一定的指导意义. 许多学者将圆管膨胀后的侧截面简化为三条线段，并基于应力平衡对膨胀稳态力进行理论解析；但是，该简化几何模型与圆管膨胀区域实际形状相差较大，管壁的弯曲变形被忽略[9-12]. LUO等[13]基于小挠度假设，根据板壳理论建立控制方程对圆管膨胀的整个过程的膜力和弯矩进行分析，建立相应的理论模型. 但上述的模型都将引入复杂的偏微分方程，以对稳态力进行求解. LIU等[14]首次提出将膨胀后圆管的轴向侧截面简化为两段曲率半径相等的圆弧和一条线段，该简化模型与实际几何形状更为贴近，并基于刚塑性材料和能量守恒进行理论推导. YAO等[15]建立吸能性能参数与各影响因素之间的响应面回归模型，并结合相关目标函数对膨胀机构进行结构优化.

本文利用Abaqus/static对不同工况和材料下薄壁圆管的膨胀过程进行数值仿真，分析圆管膨胀后的几何尺寸h和D1与各影响因素之间的规律. 通过量纲分析得到圆管膨胀后的几何尺寸h和D1与各有效影响因素之间的量纲一关系；并基于刚-幂次强化材料模型和能量守恒，在LIU等提出的侧截面假设上，进一步考虑了应变强化和压模外径对两圆弧曲率半径的影响，重新建立膨胀稳态力的预测模型.

1 模型的建立

1.1 模型的建立

图1为圆管膨胀机构简图，其主要由压模和圆管两部分组成，压模的外径大于圆管的内径，压模向下挤压圆管，使圆管发生径向扩张的塑性大变形. 本文通过有限元软件Abaqus/static对圆管的膨胀进行数值仿真，其中压模设为刚体，圆管为变形体. 考虑到圆管膨胀过程的轴对称性，有限元建模采用轴对称模型(图2所示)，单元类型采用CAX8R单元，并采用罚函数进行接触定义.

图1 膨胀机构简图Fig.1 Expansion mechanism

图2 有限元仿真模型Fig.2 Finite element mode

为了验证仿真的准确性，采用文献[6]中的三个试验工况数据与数值仿真结果对照，如表1所示. 对比显示，仿真稳态力Fs与试验稳态力Fe相差不超过8%，数值仿真结果具有较好的可靠性.

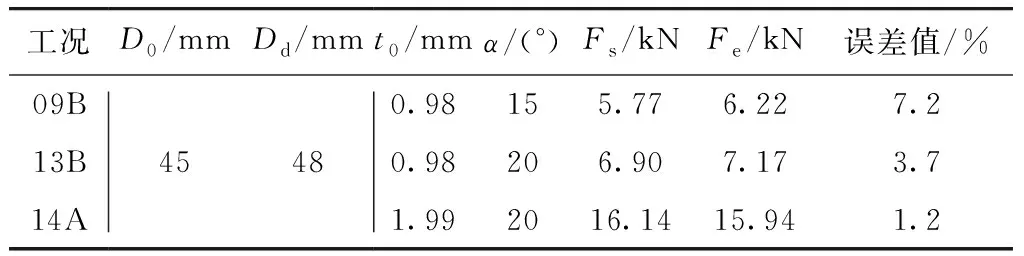
表1 仿真验证工况[6]Tab.1 Validiton works for simulation[6]

对不同工况和材料下的圆管膨胀进行数值仿真，寻找圆管膨胀后的几何尺寸与各影响因素的规律，其影响因素包括圆管内径、厚度、压模外径、压模倾斜角度、摩擦因数、材料. 将圆管的长度设置为200 mm，其足够长以避免圆管底端固支约束对膨胀的影响，压模轴向下压的位移为120 mm. 表2列出了不同工况的详细参数，A类工况只改变压模的倾斜角度，B类工况只改变圆管的厚度，C类工况只改变压模的外径，D类工况只改变摩擦因数.

表2 不同工况下圆管、压模的几何尺寸和摩擦因数

1.2 材料的选取

选取了C45钢、AA-6061铝合金、铜三种合金，用来研究圆管材料的不同对圆管膨胀后几何尺寸的影响. 三种材料的相关力学参数如表3所示. 其中，Y为屈服应力，B为硬化模量，n为硬化指数.

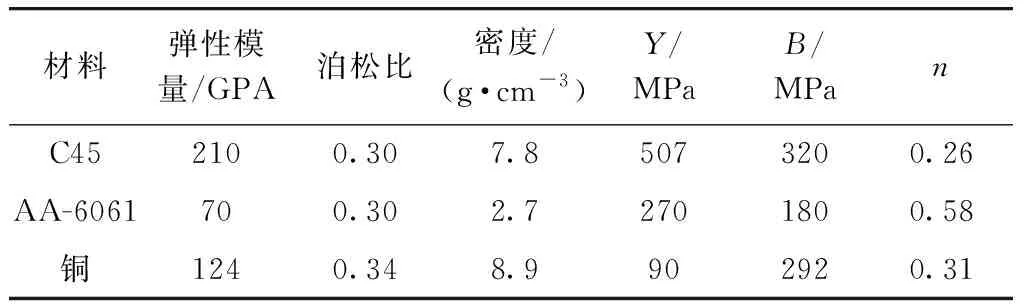
表3 各材料力学参数[16-18]Tab.3 The mechanic parameters of different materials[16-18]

2 仿真结果分析及量纲分析

图3为圆管膨胀的管壁轴向截面简图，研究不同工况下圆管膨胀后的内径D1和两弧区域C、A两点的高度差h. 图4和图5展示了不同工况下D1和h的比较，显示不同金属材料的圆管在相同的工况下膨胀，其内径D1相差不超过2%，高度差h不超过3%. 并且，由D工况数据看出，摩擦因数对圆管膨胀后几何尺寸D1和h的影响相差不超过3%. 说明材料属性和摩擦因数对圆管膨胀后的内径D1和两弧区域高度差h的影响很小，其主要受圆管和压模的几何结构影响.

采用量纲分析的方法对它们之间的关系进一步研究. 膨胀过程中的几何自变量有4个，分别为圆管的内径D0、圆管的厚度t0、压模的外径Dd、压模的倾斜角度α；因变量有2个，分别为圆管膨胀后内径D1和膨胀截面两弧度区域的高度差h.

以圆管的初始内径D0为基本物理量，根据π定理进行量纲一分析：

(1)

(2)

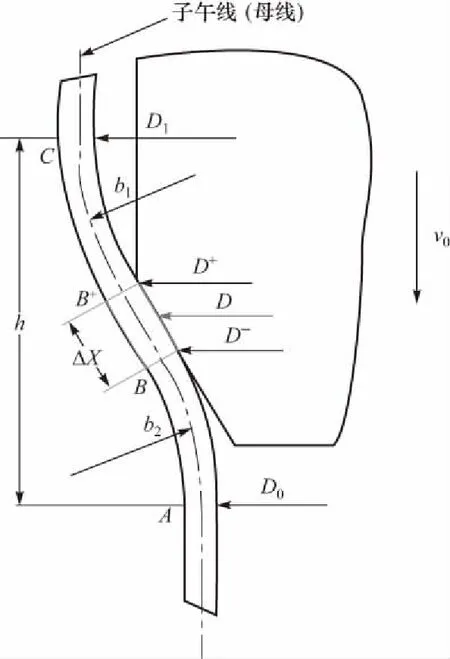
图3 轴向截面简图Fig.3 A sketch of the axial profile

当研究的量纲一参数在相对较小的范围内变化时，可对以上未知函数采用幂函数作为近似[19]. 但由文献[6]中的试验结果可知，当圆管内径一定，若圆管厚度越小，膨胀后圆管的内壁就越靠近压模的外壁. 随着厚度的减小即厚径比的减小，D1/D0存在一个极限值，其值无限接近于Dd/D0；因此在t0/D0较小的情况下，量纲一D1/D0与t0/D0之间的关系用指数函数更贴近实际情况. 因此，在这里采用了分段函数，当t0/D0≤0.06时，采用指数函数；当t0/D0>0.06时，采用幂函数. 同样，随着压模倾斜角度的减小，圆管膨胀后的内壁也会无限贴近压模的外壁.D1/D0也存在一个极限值，无限接近于Dd/D0，因此D1/D0与α之间的关系用指数函数更合适. 式(1)(2)的未知函数采用以下函数近似：

(3)

(4)

根据以上的拟合结果，可得到以下的量纲一关系式：

(5)

图4 D1与各自变量的量纲一关系Fig.4 The dimensionless relationship between D1 with independent variables

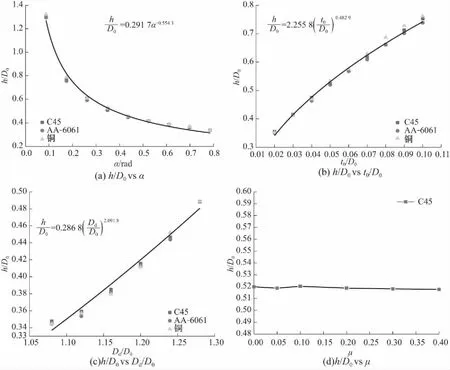
图5 h与各几何自变量的量纲一关系Fig.5 The dimensionless relationship between h with independent variables

(6)

3 解析推导

3.1 理论模型的建立

通过数值仿真，膨胀过程中管壁截面的变化能被详细观测，其膨胀的区域由一条线段和两段弧度区域组成，弧度区域的曲率半径实际上是连续变化的[11]. 为简化解析模型，做出以下几点假设：

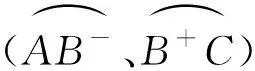
② 膨胀过程中，圆管的体积守恒(式(7)).

③ 圆管膨胀过程中母线长度保持不变，则接触部位之间的相对速度为恒值.

④ 子午线上各点的等效应力值等效代替该点所在横截面上各点的等效应力值.

根据能量守恒，圆管膨胀过程中下压力所做的功被三部分耗散掉(式(8))，分别是：拉伸耗散Eø、弯曲耗散El、摩擦耗散Ef.

v0t0(D0+t0)=vDtD(D+tD)

(7)

(8)

式中：vD为管壁相对于压模的速度；tD为管壁厚度；都是关于圆管内径D的函数.

圆管在膨胀变形过程中，忽略其弹性变形. 材料模型采用更符合材料实际应力-应变关系的刚-幂次强化模型，材料的等效应力-应变关系为

σ=Y+Bεn

(9)

式中：σ为等效应力；ε为等效应变；ø、l、t分别为圆管的环向方向、子午线方向、厚度方向(如图6所示). 由材料的不可压缩性有

εø+εl+εt=0

(10)

在圆管的子午线上，材料单元各主方向的应变分别为

(11)

因此，等效应变和等效应力分别为

(12)

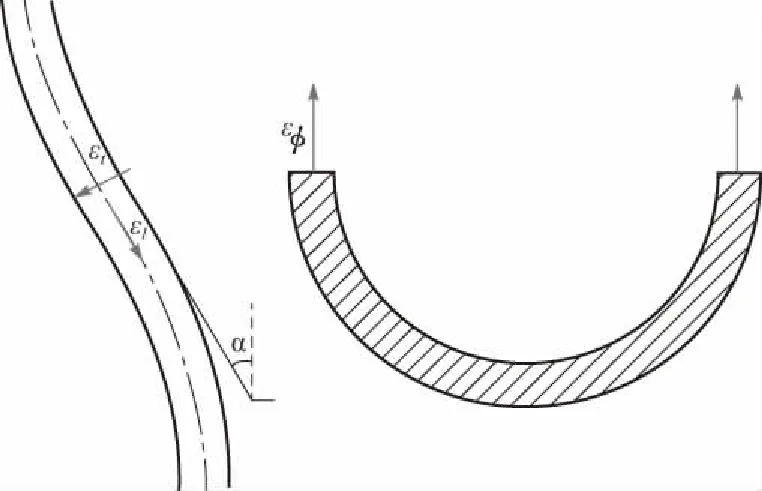
图6 各应变分量Fig.6 Strain component

(13)

圆管管壁在变形的过程中，忽略应力之间的耦合效应，则单元体积内的应变能为

(14)

式中εi代表各主应变分量.

(15)

(16)

3.2 塑性拉伸耗散

结合式(9)(11)(16)，根据体积守恒，拉伸耗散功率为

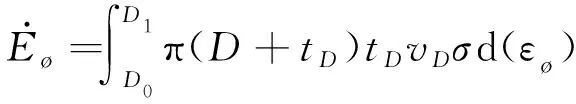
(17)

3.3 塑性弯曲耗散

在A、B-、B+和C4点的弯曲耗散功率为

(18)

(20)

(21)

根据体积守恒：

(22)

根据图中的几何特征，弧形区域的曲率为

(23)

式中ΔR=(D1+tD1-D0-t0)/2，可得：

(24)

根据做最小的原则，结合式(23)(24)，当

(25)

3.4 摩擦耗散

对圆管内壁和压模外壁接触部位做力的平衡示意图(图7所示)，根据力的平衡有：

图7 力的平衡Fig.7 The force balance

(26)

由式(26)可得摩擦力：

(27)

膨胀过程中圆管的母线保持不变，则圆管与压模的接触部分与压模的切向相对速度v0，因此摩擦耗散功率为

(28)

3.5 能量守恒

将式(17)(25)(28)代入能量守恒公式(8)，若忽略膨胀前后圆管厚度变化量，可以看成t0≈tD1. 则膨胀过程中稳态下压力为

(29)

式中，(b1+b2)和m的值可由式(5)～(6),(23)～(25)得到.

4. 理论模型的验证

4.1 与仿真结果对比

将理论模型计算出的膨胀稳态力Ft与各工况下的仿真值Fs进行比较(图8所示)，显示理论模型较好地反映出了膨胀稳态力随压模倾角、压模外径、圆管厚度、摩擦因数变化而变化的趋势，误差值小于10%.

4.2 与试验结果对比

为了进一步验证理论模型的准确度，将文献[6,11]中的各工况下的试验结果Fe与解析值Ft进行对比. 可以看出，除了04A、 05A、07A和08B工况，其他工况下误差小于14%. 其中，文献[6]中的摩擦因数是通过数值仿真与试验工况06A对照而估算出的，其摩擦因数值可能并不适用于所有的工况，从而造成一些工况下解析值和试验值有较大的误差. 整体上来说，理论解析模型能对膨胀管膨胀过程中的稳态力做较好的预测.

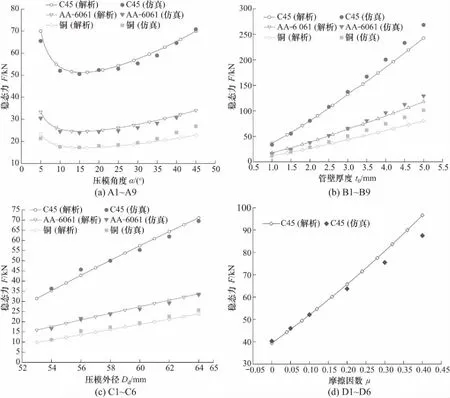
图8 理论解析解与仿真解对比Fig.8 The comparision of the analytical solutions and simulation solutions

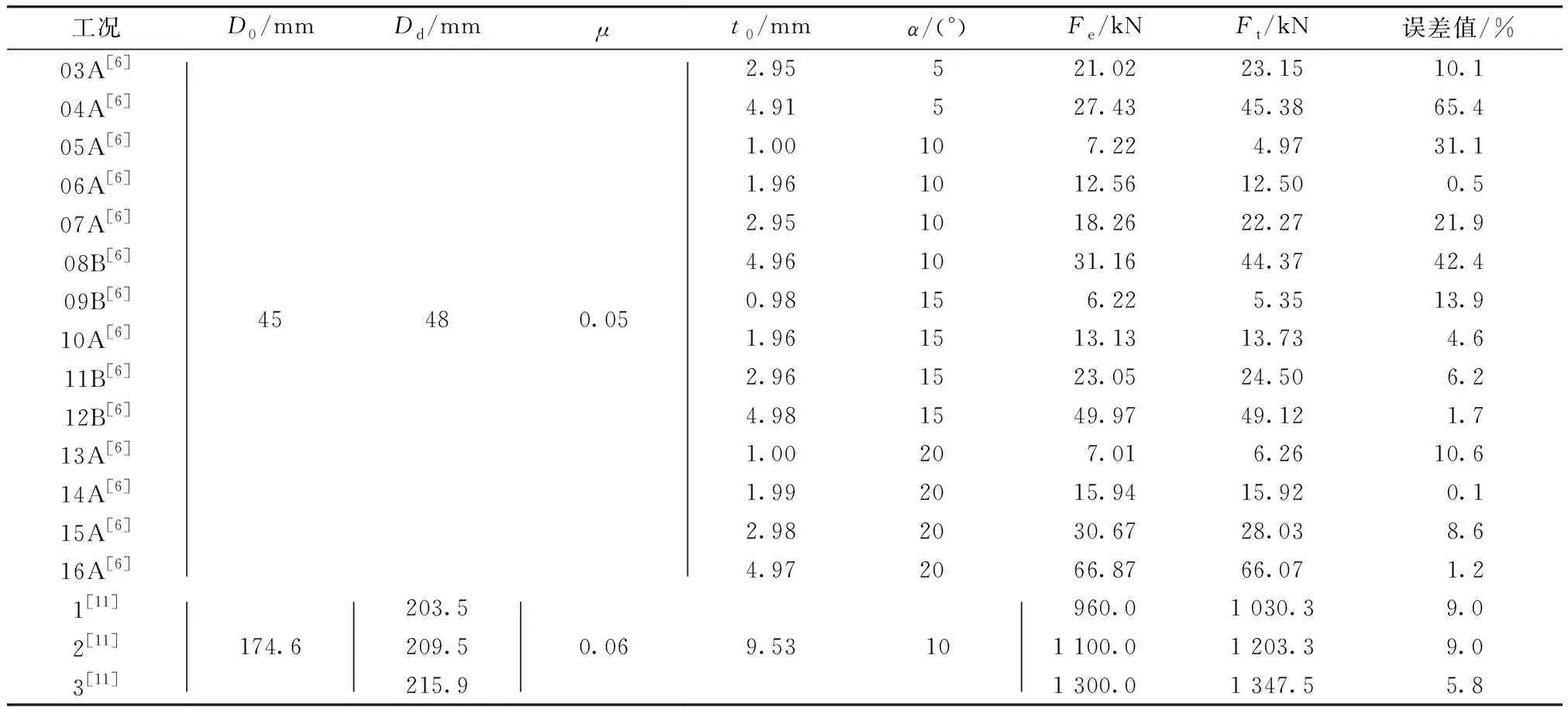
表4 解析值Ft与试验值Fe进行对比Tab.4 The comparison of the theoretical solutions Ft and the experimental data Fe

5 结 论

本文通过数值仿真软件及已有的膨胀试验对圆管的膨胀行为进行了研究，得出以下结论：

① 在膨胀变形模式下，圆管膨胀后的几何尺寸D1和h主要受圆管和压模的初始几何尺寸影响，受圆管材料和摩擦因数的影响较小. 并建立了圆管膨胀后直径D1、侧截面两弧区高度h与圆管内径D0、厚度t0、压模角度α、压模外径Dd之间的量纲一关系.