基于变值逻辑与深度学习模型的心音分类研究

姚如苹，孙 静，潘家华，王威廉**

(1. 云南大学 信息学院，云南 昆明 650500；2. 云南省阜外心血管病医院，云南 昆明 650032)

心脏听诊是临床疾病检查，尤其是各类心血管疾病初诊的基本手段[1]，如对先天性心脏病（简称先心病）的初诊和筛查主要依靠心脏听诊. 近年来，随着电子听诊器的出现，其大大方便了数字化记录心音，记录的心音信号称为心音图（Phonocardiogram，PCG）. PCG 载有心脏生理、病理的丰富信息，分析研究心音对于机器辅助诊断有重要意义. 目前，用于心音特征提取的方法主要有小波变换、频谱分析、数字滤波、梅尔倒谱频率系数（Mel Frequency Cepstrum Coefficient，MFCC）和离散傅里叶变换等[2-6]. 文献[7]首先使用小波去噪，然后提取MFCC作为心音特征后，采用支持向量机进行分类，在对异常和正常信号的分类中获得了0.93 的准确率，但当异常心音种类增多时准确率明显下降，且训练样本过少无法保证算法的普适性. 文献[8]提出了基于S 变换的心音特征提取方法，对一个周期进行S 变换，提取变换后矩阵的统计学特征，并将该特征作为区分不同信号的特征向量，但该算法对于病理性信号的特征提取较不明显，不利于后续心音分类. 文献[9-12]使用传统的机器学习方法对心音信号进行分类，如支持向量机、人工神经网络等，但得到的准确率普遍较低. 文献[13]使用深度学习方法对心音进行分类，将提取的MFCC 转换为二维特征样本，然后使用卷积神经网络对其进行分类，取得了0.895 的准确率.

上述研究中，各算法给出的准确率普遍较低，且训练样本过小，无法保证算法的普适性和鲁棒性等. 基于以上算法的不足，本文提出一种将变值逻辑模型与深度学习模型相结合的方法，将变值逻辑模型用于对心音信号的特征提取，用Inception_Resnet_v2 网络实现对先心病心音信号的分类，实验结果表明本研究取得了较高的分类评价指标.

1 分析方法

1.1 整体框架本算法主要由3 个部分组成：首先对心音信号进行预处理，滤去环境噪声和非病理性杂音，并提取心音信号的包络；然后使用变值逻辑模型进行心音信号的特征提取，得到10 个测度向量并将其进行可视化分析；最后通过深度卷积神经网络对提取到的二位样本帧进行分类，算法框架如图1 所示.

图1 整体算法分析框图Fig. 1 Block diagram of the overall analysis algorithm

1.2 实验数据实验所用的数据为云南省阜外心血管病医院和昆明医科大学第一附属医院临床采集并经医学确诊，以及在云南省各地州进行先心病筛查时采集并建立的心音信号数据库. 每例样本含临床心脏听诊5 个部位的信号，时长均为20 s 或30 s，采样频率5 000 Hz. 该心音信号数据库中，志愿者年龄2～18 岁，所有志愿者均签署知情同意书，并经过云南大学医学院伦理委员会审查同意后，授权使用. 文中共使用了1 000 例来自不同志愿者的心音信号，其中正常信号290 例，房间隔缺损（Atrial Septal Defect，ASD）220 例，室 间 隔 缺 损（Ventricular Septal Defect，VSD）270 例，动脉导管未闭（Patent Ductus Artery，PDA）220 例. 为避免模型发生过拟合，将数据集按照7∶2∶1 划分为训练集、测试集和验证集. 训练集来自700 例不同受试者的心音信号，包括200 例正常心音信号和500 例病理性心音信号. 测试集包括50 例正常心音信号和150 例病理性心音信号. 在训练过程中为了验证网络模型的有效性，采用30 例正常心音信号和70例病理性心音信号组成的数据集对其验证. 信号分布如表1 所示.

表1 心音信号集分布表Tab. 1 The distribution of heart sound signal

1.3 心音信号预处理由于采集环境的影响，心音信号往往含有背景噪声、呼吸音等非病理性噪声. 针对这类情况，使用了截止频率为25 Hz 和400 Hz的四阶巴特沃斯带通数字滤波器进行了预处理滤波.

对心音信号进行变值逻辑模型数据计算，需要对心音信号包络数据进行标记，然后对标记后的数据进行变值逻辑处理，转换为可视化分析所需要的10 个测度. 在已有的算法中，使用归一化香农能量、希尔伯特-黄变换、同态包络和维奥拉积分法提取心音信号包络都取得了不错的效果[14-16]. 维奥拉积分法是基于自适应的快速检测算法，具有处理速度快、简单并且实时性强的特点，因此本文选择维奥拉积分法作为心音信号包络的提取方法，对正常心音信号采用维奥拉积分提取到的心音包络如图2 所示. 图2(a)为未经滤波的原始心音信号，图2(b)为对应心音信号的维奥拉积分包络图. 由图2 可知，维奥拉积分包络可以很好地反映心音信号的形态学特点，有利于后续的分析处理.

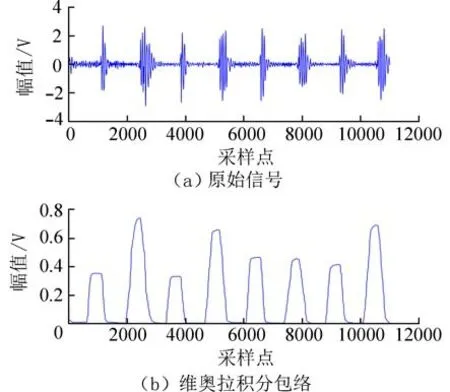
图2 维奥拉积分包络提取图Fig. 2 Diagram of Viola integral envelope extraction

1.4 变值逻辑模型

1.4.1 变值逻辑模型简介 变值逻辑理论体系[17]是在传统的逻辑映射关系“与”、“或”、“非”3 种逻辑运算的基础上引入了“置换”和“互补”等附加运算[18-19]，从而扩展了逻辑函数空间. 通过对心音信号的包络数据进行变值运算，将其转换为可视化分析的测度数据. 对心音信号数据序列进行处理的变值逻辑模型结构如图3 所示. 图3 中的计算模型（Calculation Model，CM）包括基值计算模型（Basevalued Calculation Model，BVCM）、范围值计算模型（Range-valued Calculation Model，RVCM）以及区间取值计算模型（Interval-valued Calculation Model，IVCM）. 计算模型的处理流程为：首先将心音序列通过基值计算模型、范围值计算模型、区间取值计算模型计算转换为区间取值序列，由区间的范围进一步将区间取值序列转换为由A、G、C、T 4 个碱基组成的伪DNA 序列；然后通过状态统计将其转换为计算机可识别的0-1 序列；最后计算4 个基元的概率测度.

图3 变值逻辑模型结构图Fig. 3 Structure diagram of the variant value logic model

其中，s为稳定区间值.

1.4.5 伪DNA 序列映射 经过以上3 个计算模型的处理，连续的心音信号数据序列{a0,a1,a2,···,ai,···,an} 被转换成区间取值序列R(c){c0,c1,c2,···,cj,···,cn+w-1}，对该序列的区间范围参数用

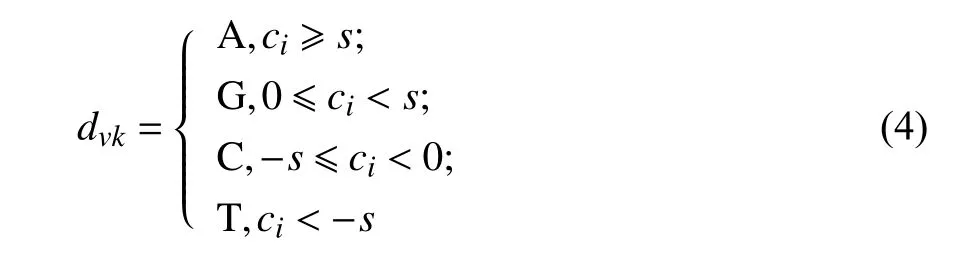
进行比较划分. 其中，i=0,1,2,···,n-w+1.

为了对数据进行有效的数学统计和保证转换出的0-1 序列中的原始信号有效信息得到最大保留，需要对伪DNA 序列进行元素标记，从而将心音信号转换为0-1 序列；同时为了使后期可视化构图表现出心音信号的特征，使用变值逻辑理论对分段后的0-1 序列进行变值转换，将其分别转换为00，01，10，11 四个元素. 设分段段长为m，第n段的数据为xi， 其相邻的第n+1 段的数据为yi，则根据测度划分规则将0-1 序列划分成为变值逻辑空间的4 种变值状态，转换规则如下：

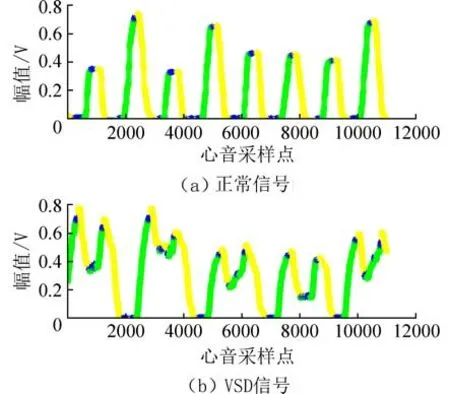
图4 心音信号的包络标记图Fig. 4 The labeled marking diagram of heart sound signal

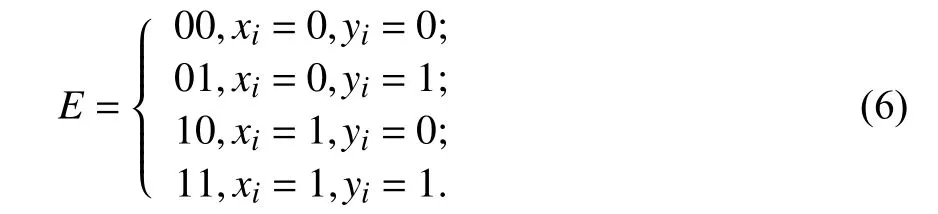
算法示意图如图5 所示.

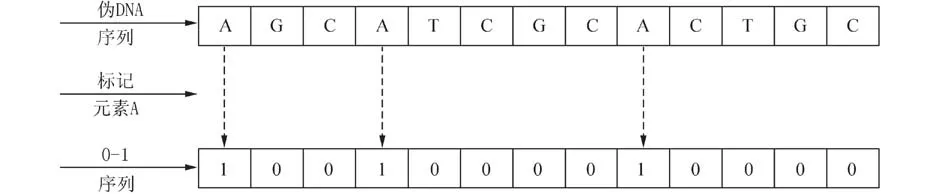
图5 0-1 序列转换图Fig. 5 0-1 sequence conversion diagram

根据心音信号包络标记特点可知，由于正常心音信号除了S1和S2以外，其他时段较为平缓，故转换出的伪DNA 序列中G 和C 元素较多，A 和T元素较少，若标记元素为A 和T，则经过0-1 序列转换出的0 较多，1 较少；而病理性心音信号在收缩期或舒张期含有病理性杂音，因此对于病理性心音信号来说，提取的维奥拉积分包络将会有更多上升和下降的幅度，转换出的伪DNA 序列中A 和T元素较多，经过0-1 序列转换出的序列中1 较多，0 较少. 通过对转换出的0-1 序列进行测度统计，则可以更直观地区别正常心音信号和异常心音信号.

1.4.7 测度统计 对转换出的0-1 序列进行测度统计，分别统计出各个分段中4 种变值逻辑状态的个数，然后计算各分段对应的测度向量，非归一化测度计算公式如（7）式所示，归一化测度计算公式如（8）式所示.

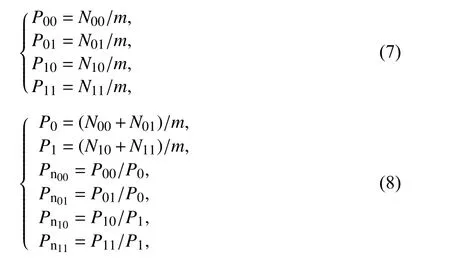
其中，m为分段段长，P00，P01，P10，P11定义为非归一化测度，P0，P1，Pn00，Pn01，Pn10，Pn11为归一化测度. 对于正常的心音信号，由于其转换出的00 较多，11 较少，故其统计出的P00，Pn00数值较大；而对于病理性心音信号，则统计出的P11，Pn11数值较大.本文将心音信号经过变值逻辑模型处理后，将正常和病理性心音信号形态上的特点转换成了测度数据并进行可视化分析，然后结合可视化结果使用分类算法，进行分类.

1.4.8 二维样本帧转换及可视化分析 为了达到可视化分析的目的，本文将标记好的维奥拉积分进行变值逻辑转换，经测度统计后，转换为二维样本帧. 选择Pn00和Pn11两个数值较大、较典型的测度向量，以Pn00为x轴，Pn11为y轴，将其转换为二维样本帧，分别绘制出其散点图与等高线图，观察其分布特征. 文中算法各参数选取为：滑动窗口值w为20，稳态区间值s为0.925，分段段长m为150.可视化测度向量选择归一化测度Pn00，Pn11和非归一化测度P00，P11. 患有ASD 和正常人的心音信号二维散点图如图6（a）和图6（b）所示，相应的等高线图如图7（a）和图7（b）所示. 图6（a）和图6（b）上半部分为经过非归一化后的二维散点图，下半部分为归一化后的二维散点图.

从图6（a）可以看出，房间隔缺损（ASD）的心音信号散点图集中在左下角的位置，而正常人的心音信号散点图则集中在左侧靠近y轴坐标轴的位置. 由于病理性信号在收缩期含有病理性杂音，因此经伪DNA 序列转换后的0-1 序列中1 较多，经过测度统计后绘制的等高线图7（b）中，ASD 信号的形状分布较广，范围更宽，且与散点图的分布类似集中在左下角的位置；而正常信号含有较少的杂音，因此绘制出的等高线图分布形状更集中，与散点图类似分布在左侧靠近坐标轴的位置.

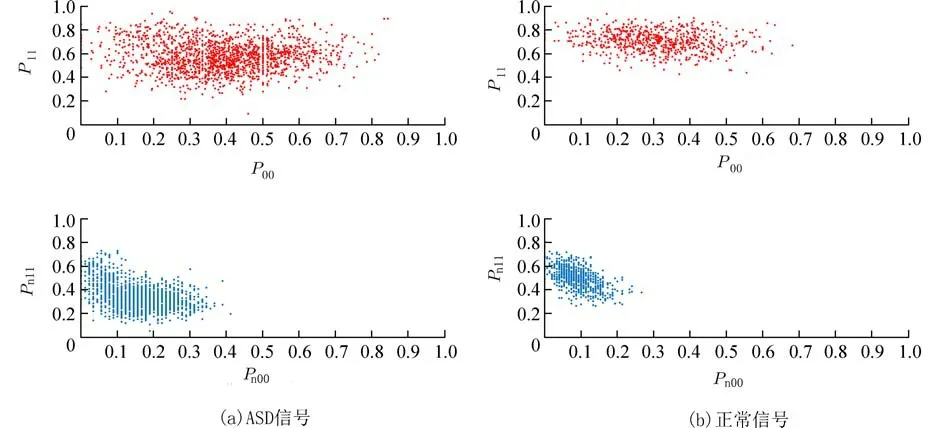
图6 ASD 信号和正常信号的二维散点图Fig. 6 Scatter of ASD signal and normal signal

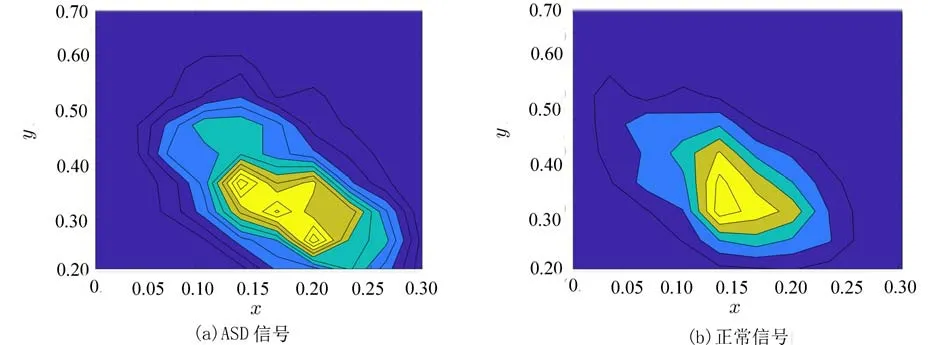
图7 ASD 信号和正常信号的等高线图Fig. 7 The contour of ASD signal and normal signal

对于后续的机器学习分类器，文中将第1.4.7节测度统计中得到的10 个测度向量保存为.csv 文件，然后将这10 个测度向量作为特征向量输入分类器进行心音分类. 对于深度卷积神经网络，文中将本节得到的二维样本帧作为神经网络的图像输入，将每一类数据按照不同文件夹存放，将其划分好训练集、测试集和验证集后转换为TFrecord 文件，送入神经网络进行后续的分类识别.

1.5 数据增强为了防止由于数据集过小带来模型的过拟合，同时增加足够的数据量并且提高分类的准确率，本文对现有的数据进行数据增强. 具体操作是将已有的图像（二维样本帧）进行水平和垂直翻转，或者对图像进行任意比例的缩放. 本文对图像进行直角旋转，旨在让网络模型学习图像的旋转不变性特征，设置数据增强因子为2，这意味着将原始数据量增加一倍.

1.6 Inception_Resnet_v2 网络Inception_Resnet_v2 网络是由Google 公司在2016 年提出来的，其结构主要由Stem 模块、Inception-Resnet 模块、Recduction 模块和Softmax 层组成，如图8 所示.Inception-Resnet 模块是该网络的特征提取模块，为了节省计算资源引入非对称卷积核的方法，将n×n的卷积使用1×n和n×1 的卷积来代替，在提高运算性能的同时加深了网络深度与非线性. Inception_Resnet_v2 是在Inception_v3 的基础上引入残差模块，将Inception 和Resnet 进一步结合，在加深网络深度的同时，避免了由于网络深度过深带来模型的过拟合和梯度下降等问题，同时引入残差模块降低了计算复杂度，增加了分类准确率.

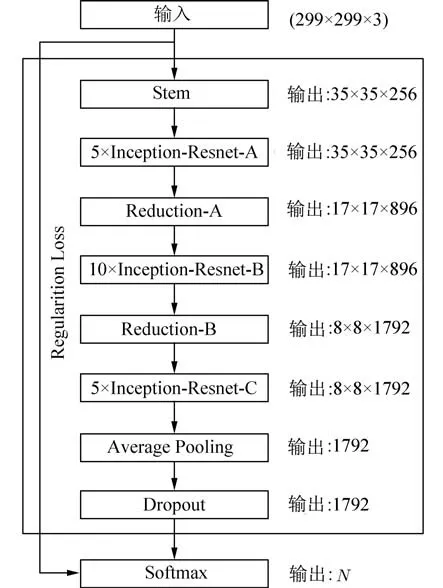
图8 Inception_Resnet_v2 结构图Fig. 8 The structure of Inception_Resnet_v2

2 实验结果与分析

2.1 训练环境实验的训练环境为深度学习开源软件TensorFlow 2.0；硬件环境为：处理器（Inter®Xeon® W-2102 CPU＠2.90GHz），显 卡（NVIDIA GeForce RTX2080），操作系统为64 位Win10. 本文使用的Inception_Resnet_v2 模型采用自适应矩估计（Adam）梯度优化算法对权重、偏置进行更新，训练迭代100 epoch，初始学习率设为0.001，当迭代到90 次时，将学习率调为0.000 1 便于网络收敛，batch size =16，输入特征尺寸为299×299.

2.2 评价标准文中将准确率（Acc）、灵敏度（RTP）和阳性预测值（VPP）作为模型的评价指标，计算公式如下：

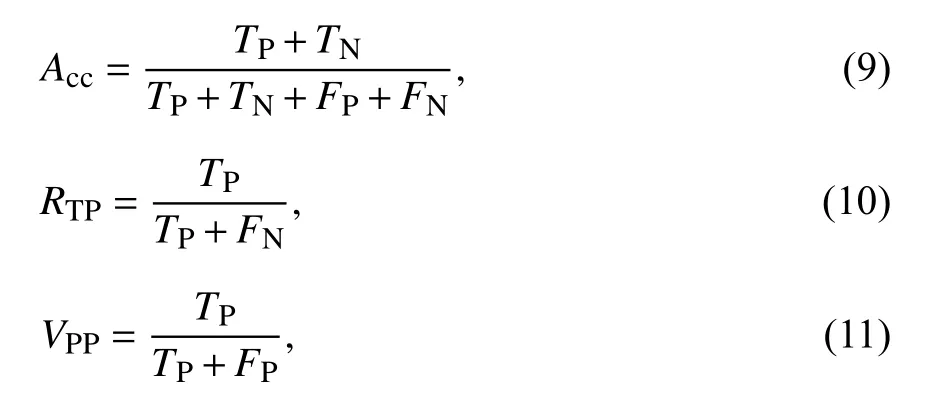
式中，TP为阳性样本预测为阳性的数目，TN为阴性样本预测为阴性负的数目，FN为阳性样本预测为阴性的数目，FP为阴性样本预测为阳性的数目.

2.3 实验结果文中选取Inception_Resnet_v2 模型作为该算法的分类器，Inception_Resnet_v2 是在Inception_v3 的基础上引入了残差网络跳跃连接的方法，对比目前较主流的CNN、LSTM、Inception等网络，Inception_Resnet_v2 在加深网络深度的同时，避免了梯度消失、 梯度爆炸的问题，将卷积核进行分解，进一步提升了计算能力和识别准确率.

文中的训练集在训练过程中自适应调整神经网络的参数与权重，验证集在训练过程中用来查看训练效果，防止网络产生过拟合，测试集在训练结束后用来测试网络的实际分类效果. 因此，在测试集上对常见的先心病信号进行多分类的实验结果如表2 所示. 由表2 可知，在对先心病心音信号的分类中， 本算法在测试集上取得了0.931 的平均准确率、0.954 的平均敏感性和0.967 的平均阳性预测值.

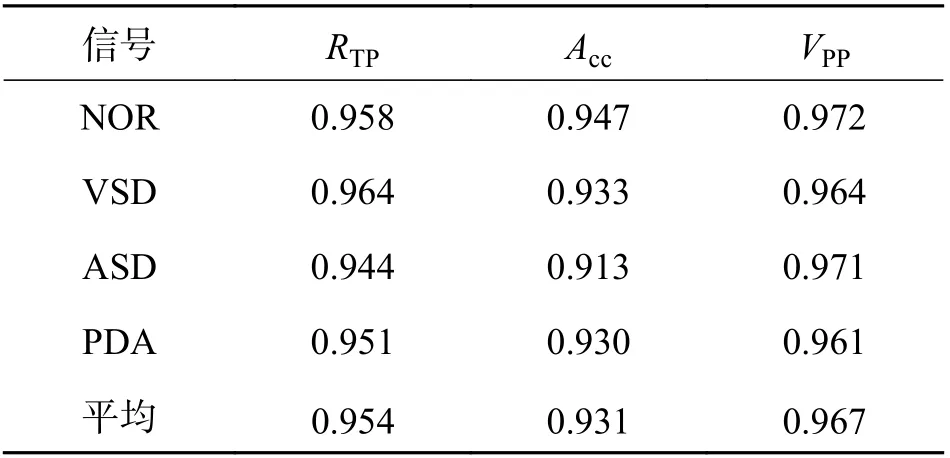
表2 先心病心音信号多分类结果Tab. 2 Multi-classification result table of congenital heart disease heart sound signal

在测试集上使用不同的特征提取方法与文中所用特征提取算法相比的实验结果如表3 所示.表3 展示了本文的特征提取算法与传统的特征提取方法相比在对先心病心音信号分类上的有效性.其中，使用传统的小波技术与MFCC 特征提取方法与使用变值逻辑模型作为特征提取方法相比，使用变值逻辑模型算法的准确率增加了0.033 和0.039.

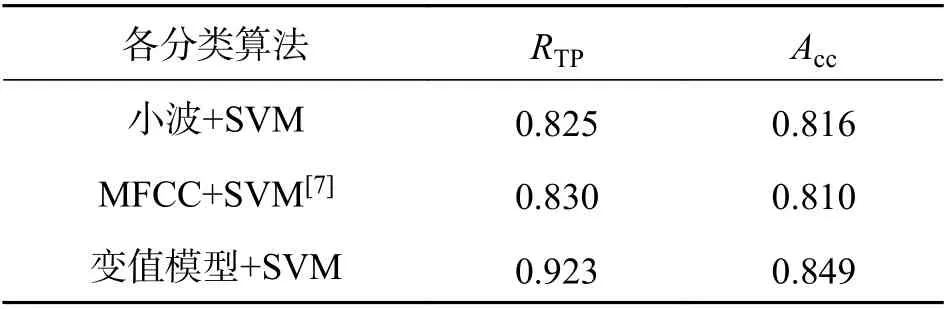
表3 不同特征提取算法对比Tab. 3 Comparison of different feature extraction algorithms

使用不同的深度学习模型在相同测试集上的实验结果如表4 所示. 表 4 展示了使用不同的深度学习模型对信号进行分类的准确率差异较大.其中相比于轻量级神经网络Mobilenet_v2，本文的准确率增加了0.139；与Inception_v3 网络相比较，Inception_Resnet_v2 将Inception 结 构 和Resnet 结构相结合，在Inception_v3 的基础上增加了残差模块，使其准确率进一步增加，本文的准确率增加了0.055. 同时，表4 与表3 对比可知，使用机器学习模型，如SVM 作为分类器的算法与本文使用深度学习模型作为分类器的算法相比，本文的准确率上升了0.082.

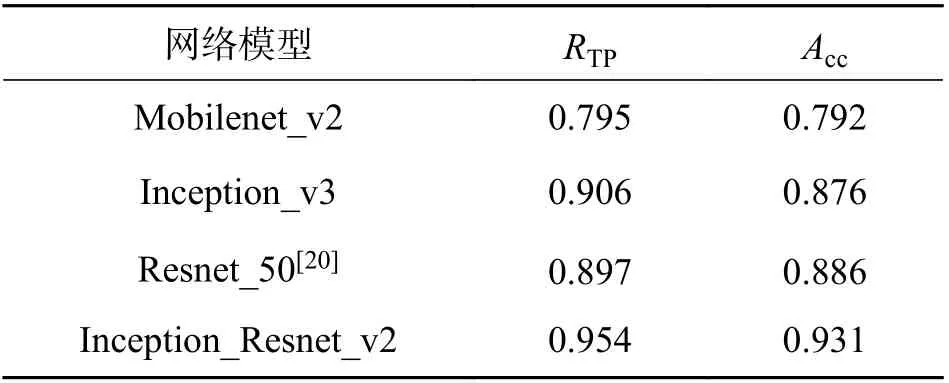
表4 不同深度学习算法对比Tab. 4 Comparison of different deep learning algorithms

3 结论

文章对心音信号进行分析处理，提出了一种基于变值逻辑模型的先心病心音分类算法. 该算法主要分为3 个阶段：第1 阶段对心音信号进行去噪和包络提取；第2 阶段将包络数据进行测度统计，使用变值逻辑模型将其转换为反映心音形态学特征的特征图也即二维样本帧；第3 阶段使用深度学习模型，本文选取Inception_Resnet_v2 网络将变值逻辑模型提取到的特征图进行图像多分类. 实验结果显示，该算法得到了较高的分类准确率，该算法对常见先心病心音多分类的平均准确率为0.931，平均灵敏度为0.954，平均阳性预测值为0.967. 与传统的机器学习方法相比，本文选用深度学习模型作为分类器，网络层数更深，学习到的特征更加丰富，准确率提升了0.082. 实验结果显示，变值逻辑模型与Inception_Resnet_v2 网络结合提高了分类准确率，且该算法是在大样本环境下测试得到，保证了算法的普适性和鲁棒性，有望用于先心病初诊的机器辅助诊断.