双声道心音能量熵比的提取与识别研究

孙科学，魏 敏，宋江珉，李子炎，成雨含

(1.南京邮电大学 电子科学与工程学院，江苏 南京 210023;2.江苏省射频集成与微组装工程实验室，江苏 南京 210023;3.南京邮电大学 信息化建设与管理办公室,江苏 南京 210023)

双声道心音能量熵比的提取与识别研究

孙科学1,2，魏 敏1，宋江珉1，李子炎1，成雨含3

(1.南京邮电大学 电子科学与工程学院，江苏 南京 210023;2.江苏省射频集成与微组装工程实验室，江苏 南京 210023;3.南京邮电大学 信息化建设与管理办公室,江苏 南京 210023)

研究了双声道心音的能量熵比提取与分类识别的基本原理和实现方法。分析了心音信号特性及提取双声道心音特征值的可行性和必要性。为了减少特征值的计算量，又能使特征值体现出时域和频域的不同特点，提出了双声道心音能量熵比的概念并详细地阐述了其计算过程。分别取单声道心音时域能量熵比和频域能量熵比，双声道心音的能量熵比为两个单声道心音能量熵比的均值。将双声道的能量熵比作为特征值识别双声道心音。然后通过相似距离法针对双声道心音能量熵比进行双声道心音的分类识别。实验结果表明，双声道心音能量熵比能全面地反映双声道心音的时频域特点，不仅有利于心音的分类识别，而且降低了特征值的维度，使得计算量减小，提高了识别效率和实用性。

双声道心音；能量熵比；相似距离；分类识别

0 引 言

生物特征识别技术是利用计算机技术对人的生理特征或行为特征进行检测并鉴定身份的技术。选择合适的生物特征对身份鉴定的结果有至关重要的作用。从广义上讲，生物特征可以分为与生俱来的生理特征和后天的行为特征[1]。心音和已有的语音、指纹、视网膜等常见的生物特征一样，有不易被遗忘、窃取和破解的特点，具有较高的保密性和安全性，近年来国际上也开始采用心音作为一种生物特征来进行身份识别。

心音信号是人体最重要的生理特征之一，它是由心动周期中心肌收缩舒张、瓣膜启闭以及血液冲击心室壁和大动脉等引起的机械振动而产生的[2-4]。从物理上看，它反映了心脏和心血管系统机械运动的状况，包含心脏各部分如心房、心室、大血管、心血管及各个瓣膜功能状态的大量的生理信息。这些信息时刻都在变化，对于个体来说都是独一无二、各不相同的。由此可见，心音信号具有普遍、独立、唯一的特点。心音在时频域具备稳定性和可采集性，这使得它能够作为生物特征被识别和研究。这不仅为身份识别提供了新思路，也推动了临床医学中心音听诊的发展。

目前已有不少国内外学者针对心音信号的采集、预处理、特征提取方法以及身份识别方法进行了研究。John C.Wood等对第一心音的时域和频域的动态特性进行了深入研究[5]；成谢锋等不仅采用独立子波函数算法提取心音特征，对基于数据融合的三段式心音身份识别技术等也进行了研究[6-7]，还将心音分析识别系统与LabVIEW平台和Android平台相结合，大大提高了心音在实际生活中的应用范围[8-9]。

但大多数研究是针对单声道心音的特征提取进行，只能对采集的一路心音信号进行分析处理，不能全面及时地反映心脏在同一时刻不同部位的情况，有一定局限性。而双声道[10]心音可同时在心脏的不同部位采集两路心音信号，使得采集到的信息更加丰富、全面、完整。所使用的双声道心音是通过两个心音传感器同时采集两路心音作为左右声道得到的。通过对两路心音同时提取时频能量熵比，并将两路心音各自的特征值融合后采用相似距离法进行识别，能提高识别的准确性和可靠性，对心音身份识别具有积极意义。

针对双声道心音的特征提取问题，引入双声道心音能量熵为特征值，提出了双声道心音的分类识别算法，并通过实验对该算法进行验证。

1 双声道心音特征提取的方法

心音的特征参数可以有效地体现不同个体心音的特点，因此合适的特征参数在心音特征提取和分类识别研究中具有非常重要的作用。选择适当的特征参数可以提高心音的识别率。特征参数选取应遵循以下原则：不同个体之间的心音距离要尽可能大，同时同一个人的心音之间的距离应尽可能小；要在保证提高识别率的情况下，尽可能减少特征参数的维数，从而减少特征参数的计算量，这样不仅便于实现、方便存储数据，也提高了识别效率。

心音信号的特征一般分为时域特征参数和频域特征参数。为了更好地反映出心音信号在时频域的特征，以将时域和频域中S1心音和S2心音相融合的双声道心音能量熵比作为特征值，对双声道心音进行分类识别。

1.1 能量熵

熵具有非线性的特点，被广泛应用于概率论、生命科学等领域，近年来也被用于心电信号的研究中。Pincus[11]于1991年提出了近似熵(Approximate Entropy，ApEn)理论。近似熵具有运算简单、抗噪声等优点[12]。已尝试采用ApEn作为特征值进行提取，但是，近似熵统计量很容易导致结果不一致。于是采用更为简单且能充分反映信号能量概率分布均匀程度的能量熵[13]表征心音在时域和频域的能量分布情况。能量熵的熵值大小反映了信号能量概率分布的均匀程度，心音在时域和频域的能量分布具有独立性和随机性，能量熵能体现出个体心音能量分布的微小差异。第一心音和第二心音的能量熵比为无量纲值，使得数据存储和运算更为简便。且相对于能量，熵值在某些情况下具有更好的鲁棒性。

1.2 能量熵比提取过程

心音信号的时域波形包含着个体的生物特征，是身份识别的重要依据，存在客观真实性。但如果直接将采集到的心音信号用于身份识别或是采用智能处理方法自动提取特征值，不仅计算量较大，也使得后期的信号更加复杂。由于心音信号具有周期性且为时变信号，第一、二心音信号S1和S2的开始与终止特征明显且在S1和S2期间不会产生突变，而第三、四心音S3和S4的信号较弱。如果以一个固定的且较短的时间窗观察心音信号，则可以得到一系列近似稳定的信号，即心音信号变成时准稳定的，所以可用心音信号子波族去合成模拟一组心音。根据心音的特性，采用一种心音信号模型[14]来简化心音信号。

设原始心音信号为{x(1),x(2),…,x(N)}，按照以下步骤计算时域和频域能量熵。

一个周期的心音信号由第一、第二心音S1、S2和第三、第四心音S3、S4以及心音杂音S5组成，因此一个周期的心音信号可近似表示为：

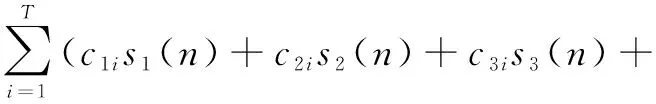
c4is4(n)+c5is5(n))

(1)

根据心音的物理特性，心脏收缩产生的第一心音S1和心脏舒张产生的第二心音S2都能通过胸腔传到体表。实验结果表明，S1和S2的能量会随着心脏收缩和舒张的强度的变化而发生变化，但二者能量的比值基本保持恒定，这个比值可以作为生物特征进行识别。因此采用S1心音和S2心音的能量比作为信号的参数特征。第i个周期中的时域第一和第二心音的幅值比即FSR，体现了第一心音和第二心音在时域的能量分布，则时域能量熵比可描述为：

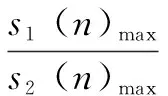
(2)

S1与S2心音的能量比是一个无量纲值，对于每个人来说，其值可看成近似不变的。若心音数据库较小，用FSR作为心音特征是简单可行的，但较小的心音数据库不满足广泛应用的要求；而当心音数据库较大时，会出现多个个体FSR值近似或相同的情况，降低了识别率。

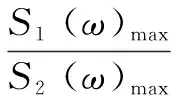
(3)

考虑到提取和识别特征值的运算速度，决定采用较为简单快捷的融合算法。由于心音时域和频域中的特点对识别分类的影响同样重要，且时域和频域的能量熵比都为无量纲值，因此采用加权平均融合的方法将时频域中的能量熵比进行融合，融合后的单声道心音能量熵比可表示为：

(4)

图1 双声道心音能量熵比的提取过程

2 心音分类识别

2.1 分类识别方法

身份识别是在已经建立的生物特征数据库中找到与待识别用户相匹配的用户，以确定待识别用户的身份。因此心音身份识别过程也应分为两步：一是通过心音传感器采集用户的心音信号数据，并对原始心音信号进行预处理，然后提取特征值，将特征值和用户信息存储在模板数据中，并建立双声道心音数据库；二是在心音识别阶段，采集待识别用户的心音并对心音进行处理，将心音特征值与数据库中的模板一一比对，以确认待识别用户的身份。因此心音识别过程简单来讲就是一个模板匹配的过程，就是让计算机通过信号分析处理判别被识别用户的身份，在建立较大心音数据库的前提下，使用机器识别身份或心音听诊较人工而言更加快速准确。在心音识别领域，不同的特征提取方法对应着不同的识别方法。比如基于距离的识别方法和基于神经网络的识别方法。虽然具体实现时存在差异，但基本的技术是类似的。

根据心音分类识别的基本方法，需要将待识别人的心音特征与心音数据库中的特征模板进行匹配，再根据相关判别法则，判断待识别的心音属于心音数据库中的哪个用户，以便确认其身份。模式识别方法大致有如下几种：欧氏距离法、高斯混合模型(GMM)和矢量量化(VQ)法、相似距离法和神经网络识别法等。采用相似距离法[15]来度量两个信号谱之间的距离。

设标准组的心音信号为ci(t)，待识别信号为sj(t)，则相似距离定义为：

(5)

通过定义相似距离来辨别两个心音信号。辨别方法如下：ci(t)与sj(t)之间的相似距离dk越小，则ci(t)与sj(t)越相似；当dk=0时，ci(t)=sj(t)，表示待识别信号与标准信号相同。将待识别的心音信号与数据库中的心音信号一一对应进行模式匹配，可找出它们的相似距离。

具体的双声道心音分类识别过程如下：首先采集20路单声道心音(即10组双声道心音样本)建立心音数据库，然后根据心音信号的周期性，对各组双声道心音的两路心音分别截取5个单周期样本并计算出5个双声道心音能量熵比，取其平均值作为此类心音的中心。最终得到10个双声道心音样本的类中心。测试时，要先计算出待识别的双声道心音信号的能量熵比，再求出数据库中各个类中心特征值与待识别特征值之间的相似距离，最后将待识别双声道心音归为对应相似距离最小的那一类中。

2.2 系统性能评价

完成心音的分类识别后，需要对识别方法进行评价。心音身份识别有这两种形式的评价指标：身份确认和身份辨识。在一对多的情况下，即从心音数据库中的众多用户中确认待识别用户的对应身份，采用识别率来表示以双声道心音能量熵比作为特征值进行识别的准确程度。

正确识别率(Correct Recognition Rate，CRR)[13]可用来评价系统性能优劣，如式(6)所示：

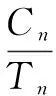
(6)

其中，Cn为被正确识别的样本数量；Tn为测试样本总数量。

在实验测试中，已知每组待识别用户的身份，同时也记录模板匹配的结果，检测心音身份识别的结果是否可靠，并对所有测试结果的正确性做出统计。

3 识别实验

采用的心音数据库来源于实测的10个正常人的20路心音信号，其中每个人采集两路心音信号，采样频率为8 kHz。心音信号的采集过程易受到外界因素的影响，引入了各种噪声，因此在提取特征值之前需要进行预处理，主要包括归一化和低通滤波去噪[16]。考虑到心音的频率特点，心音信号的频率约为10～1 000 Hz，主要集中在300～500 Hz之间。其中第一心音S1主要集中在中低频范围，且具有持续时间长、音调低等特点，其波峰的低频范围为10～50 Hz，中频范围为50～140 Hz；而第二心音S2在低中高频范围内都有分布，持续时间短，频率高，其波峰的低频范围为10～80 Hz，中频范围为80～200 Hz，高频范围为220～400 Hz。这里主要对中低频范围的心音进行预处理，因此将低通滤波的截止频率设定为150 Hz。

特征值提取过程仅以双声道中的一路心音为例，其他路心音信号的特征值提取过程依此类推。由图2可看出，第一心音和第二心音幅度的最大值，通过Matlab读取最大值即可计算出第一心音和第二心音的幅值比即时域能量熵比。然后使用傅里叶变换，将上述经过预处理后的第一心音和第二心音分别变换到频域中，其频谱如图2(a)、(b)所示。再通过Matlab得到幅频图上S1和S2幅度的最大值，即可计算出频域能量熵比和时频能量熵比。来源于同一人的另一路心音也采用同样的方式计算出时频能量熵比，最后将两路心音的时频能量熵比进行融合，得到最终的双声道心音特征值。

图2 第一心音和第二心音的幅频特性图

待识别心音也按上述方法提取特征值后，将待识别特征值与数据库中的特征值进行匹配，计算待识别心音特征值与数据库中每个类中心之间的相似距离。测试时，共进行了20次识别实验，实验数据如表1所示。表1中只选取前5个样本。实验结果表明，在20次实验中，使用双声道心音能量熵比作为特征值进行识别，其中有17次能将待识别双声道心音成功匹配给原本被采集心音的用户，CRR可达85%，基本达到了可实际应用的阶段。由此可以看出，该方法在保证识别率的情况下，减小了数据计算量和复杂度，提高了识别速度。

表1 实验数据

4 结束语

提出了一种针对双声道心音的特征提取和分类识别方法。通过分析心音信号在时频域的不同特点，提出使用双声道心音能量熵比作为双声道心音的特征值，并具体阐述了双声道心音能量熵比的概念和计算方法。双声道心音能量熵比不仅能体现出心音的时频域特性，有利于心音分类识别，而且降低了特征值的维度，减小了计算量，提高了识别效率和实用性。另外，通过相似距离法对心音进行分类识别，使得计算代价减小，在保证识别率的前提下，大大提高了识别速度。实验结果表明，使用双声道心音能量熵比作为双声道心音特征值具有较高的可靠性和可操作性，为心音身份识别的实际应用和心音信号的识别研究开辟了新途径。

[1] 孙冬梅，裘正定.生物特征识别技术综述[J].电子学报，2001，29(12A)：1744-1748.

[2] Monali U M,Aparana R S.Review on heart sound analysis technique[C]//Proceedings of international conference on internet computing and information communications.India:[s.n.],2014:93-101.

[3] Chen D,Durand L G,Lee H C.Time-frequency analysis of the first heart sound.Part1:simulation and analysis[J].Medical and Biological Engineering and Computing,1997,35(4):306-310.

[4] Wood J C,Barry D T.Time-frequency analysis of the first heart sound[J].IEEE Engineering in Medicine & Biology,1995,14(2):144-151.

[5] Wood J C,Buda A J,Barry D T.Time-frequency transforms:a new approach to first heart sound frequency dynamics[J].IEEE Transactions on Biomedical Engineering,1992,39(7)：730-740.

[6] 马 勇,成谢锋.独立函数元:模型、方法和应用[J].物理学报，2014,63(6):357-363.

[7] 成谢锋,马 勇,张少白,等.基于数据融合的三段式心音身份识别技术[J].仪器仪表学报，2010,31(8)：1712-1719.

[8] 张会香,成谢锋.LabVIEW平台上的心音分析虚拟仪器设计[J].计算机技术与发展，2010，20(11)：217-220.

[9] 成谢锋,刘 伟.基于Android平台的心音识别系统的研究[J].计算机技术与发展，2015，25(2)：152-155.

[10] 李俊梅,俞 锫.双声道立体声拾音技术研究[J].北京广播学院学报:自然版，2001(2)：34-40.

[11] Pincus S M．Approximate entropy as a measure of system complexity[J].Proceedings of the National Academy of Sciences of the United States of America，1991，88(6):2297-2301.

[12] 赵海龙，穆志纯.基于小波变换和LDA/FKT及SVM的人耳识别[J].仪器仪表学报，2009，30(11):2273-2278．

[13] 张小蓟，张 歆，孙进才.基于IMF能量熵的目标特征提取与分类方法[J].计算机工程与应用，2008,44(4)：68-69.

[14] 成谢锋，马 勇，刘 陈，等.心音身份识别技术的研究[J].中国科学：信息科学，2012,42(2)：237-251.

[15] 成谢锋，傅女婷.心音身份识别综述[J].上海交通大学学报，2014，48(12):1745-1750.

[16] 朱冰莲，刘 倩.心音信号的自适应小波去噪[J].计算机技术与发展，2006，16(10)：83-84.

ResearchonFeatureExtractionandIdentificationwithSpecificEntropyofDualTrackHeartSound

SUN Ke-xue1,2，WEI Min1，SONG Jiang-min1，LI Zi-yan1，CHENG Yu-han3

(1.School of Electronic Science and Engineering，Nanjing University of Posts and Telecommunications，Nanjing 210023,China；2.Jiangsu Province Engineering Lab of RF Integration & Micropackage,Nanjing 210023,China；3.Office of Informatization and Management，Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

The fundamental principle and implementation method of extracting energy entropy ratio and classification recognition from the dual track heart sound are researched.The feasibility and necessity of characteristics of heart sound and extracting dual track heart sound features have been analyzed.In order to reduce the calculation of eigenvalue and show its characteristics in time and frequency domain,the concept of energy entropy ratio for dual track heart sound is presented and its computational process is discussed in detail.After calculating the energy entropy ratio of the mono heart sounds in time and frequency domain,the dual track heart sound energy entropy ratio is the average of them.Then the method of similarity distance is applied to classify and recognize the dual track heart sound.The experimental results show that the characteristics in time-frequency domain of dual track heart sound can be reflected comprehensively by the energy entropy ratio,which is not only beneficial to the recognition of heart sound,reducing the eigenvalue dimensions,but also make it possible to reduce amount of calculation and improve the recognition efficiency and practicality.

dual track heart sound;energy entropy ratio;similarity distance;classification recognition

TP311.1

A

1673-629X(2017)12-0166-04

10.3969/j.issn.1673-629X.2017.12.036

2016-03-03

2016-06-22 < class="emphasis_bold">网络出版时间

时间：2017-08-01

国家级大学生创新创业训练计划(SZDG2016009)；江苏省高校自然科学研究面上项目(15KJD510001)；南京邮电大学实验室工作研究重点课题(2016XSG02)

孙科学(1981-)，男，副教授，研究方向为电子电路设计、智能信号处理嵌入式系统与通信软件设计。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170801.1550.028.html