时标上具有捕获率和投放率的Holling Ⅲ型捕食系统的周期解

姜全德

(广东轻工职业技术学院 财贸学院 数学教研室，广东 广州 510300)

近年来，很多学者研究了连续或离散情况下的捕食系统[1-15]. 同时，时标理论也吸引了不少学者.2006 年，Bohner 等在文献[1]中首次应用重合度延拓定理研究了时标上微分方程的周期解的存在性问题.目前，关于时标上研究捕食系统的周期解已有不少结果[2-3,9,14].

2009 年，Wang 等在文献[2] 中研究了以下捕食系统

其中x(t),y(t) 分别表示食饵和捕食者的密度，ri,bi,ci都是正的周期为 ω 的函数，分别为幼年食饵的内蕴增长率、俘获率、成年捕食者的自然死亡率；k＞0,0 ＜m≤1.

如果系统在人为干预情况下，有投放食饵和捕获捕食者的情况，又因现实生活中各种现象存在时间延迟，所以考虑时滞因素. 系统（1）可以写成

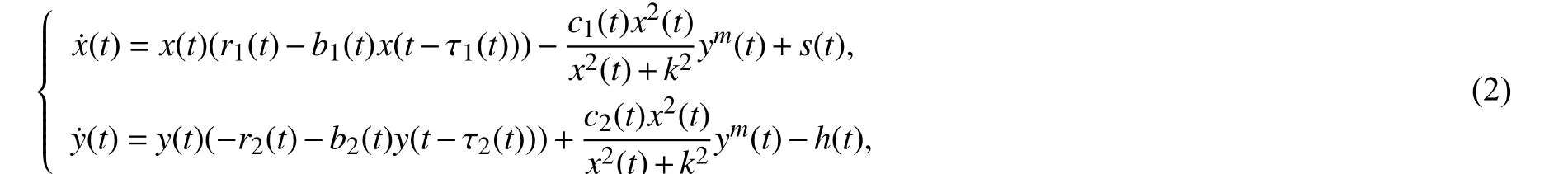
其中s(t),h(t) 都是正的周期为 ω 的函数，分别表示食饵种群的投放率和捕食种群的收获率.

本文将在时标上研究下列系统

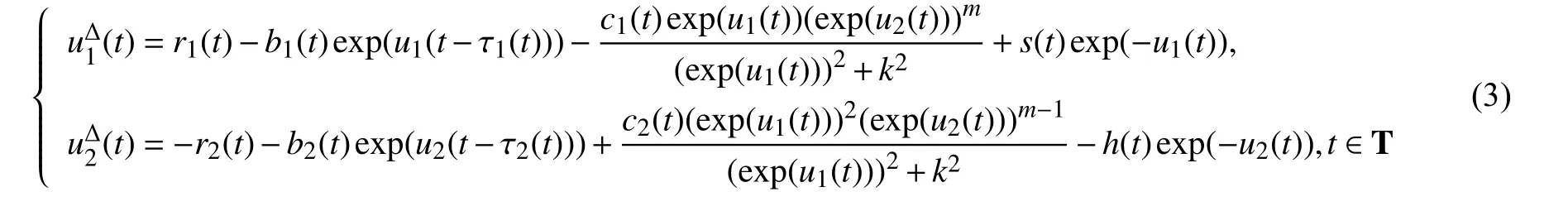
的多周期解的存在性问题，其中 T 为任意时标.

如果令x(t)=exp(u1(t)),y(t)=exp(u2(t))， 当 T =R ( 实数集)时，系统（3）就变成了系统（2）.当 T =Z(整数集)时，系统（3）就变成了离散系统

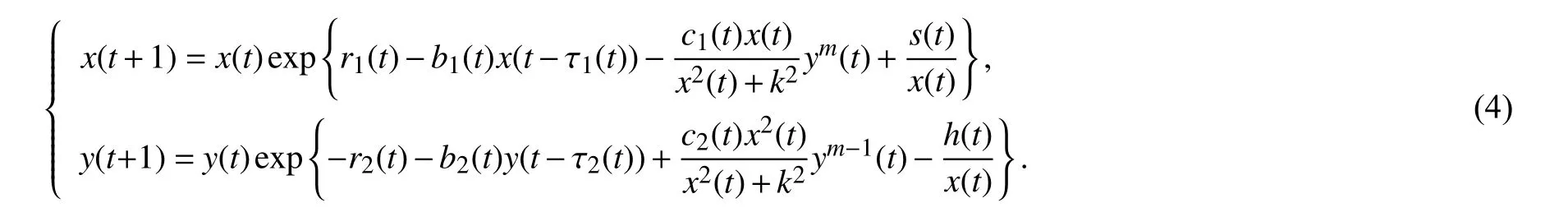
1 预备知识

2 主要结果

首先定义

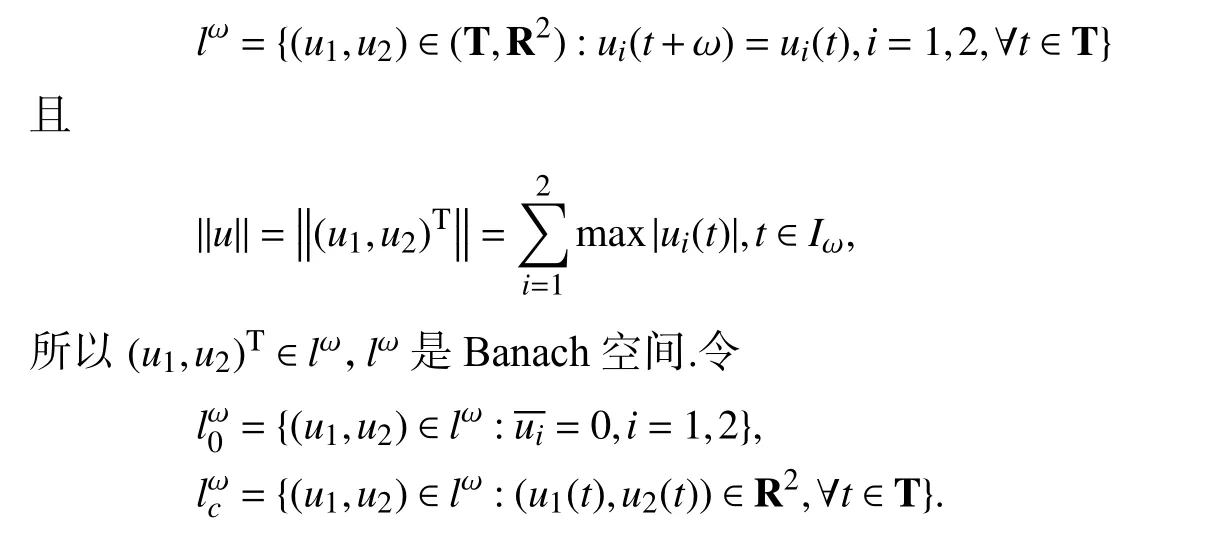
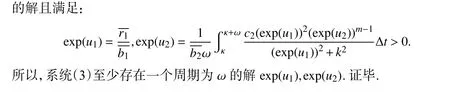
3 总结

本文研究时标上具有捕获率和投放率的 Holling-Ⅲ 型捕食系统，考虑了时滞效应，基于时标Mawhin重合度理论方法，得到了系统至少有一个正周期解.