基于等效电路法复合变幅杆的优化设计
2021-10-13巩建辉喻刚强严碧歌
巩建辉,喻刚强,姚 静,严碧歌
(1.商洛职业技术学院,陕西 商洛 726000;2.陕西师范大学物理学与信息技术学院,陕西 西安 710062)
0 引言
变幅杆具有振幅放大作用,是超声加工系统中的重要部件,随着超声系统应用的日益广泛,对变幅杆的放大倍数及性能指标要求越来越高,单一变幅杆因为放大系数有限不能满足实际生产的需要,所以从单一变幅杆发展到了复合变幅杆。为了获得性能优良的变幅杆,广大学者对新型变幅杆的设计和研究从未停止,赵洪博等[1]利用替代法设计了宽端接圆柱杆的悬链形复合变幅杆;靳涛等[2]将圆柱和圆锥杆进行组合,对圆锥复合变幅杆进行了研究;崔晓娟等[3]将指数杆和圆锥杆进行组合,对指数复合变幅杆进行了优化设计;孙涛等[4]设计了正弦圆柱形复合变幅杆,该变幅杆的放大倍数和形状因数皆优于阶梯形变幅杆。本文采用等效电路法设计了一种半波长复合变幅杆,即指数悬链线形复合变幅杆,得出了该变幅杆的频率方程以及放大倍数,并对变幅杆进行了优化设计和有限元分析。
1 变幅杆的模型构建
该复合型变幅杆由指数杆Ⅰ和悬链线杆Ⅱ组合而成,如图1所示。指数杆的长度为l1,大小端面的面积分别为S1和S,大小端面的半径分别为R1和R。悬链线杆的长度为l2,大小端面的面积分别为S和S2,大小端面的半径分别为R和R2。
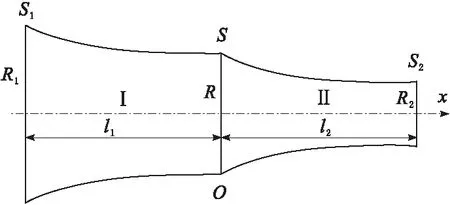
图1 指数悬链线形复合变幅杆模型
2 变幅杆的设计理论
2.1 等效电路法
变幅杆常用的设计方法有解析法、等效电路法、替代法、传输矩阵法、分段趋近法和表观弹性法等[5],其中等效电路法设计思路清晰、物理意义明确,故采用等效电路法对指数悬链线形复合变幅杆进行理论分析。所谓等效电路法就是对于任何一个单一形状的变幅杆,通过力电类比都可以等效为一个四端网络电路模型,如图2所示[6]。图2中,F1和F2是变幅杆两端所受的力,相当于电路中的电压;v1和v2为变幅杆两端的振速,相当于电路中的电流;Z1、Z2和Z3为力阻抗,相当于电路中电阻抗。
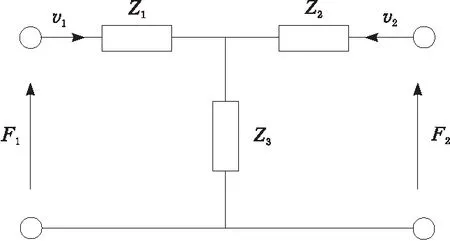
图2 等效四端网络电路模型
2.2 复合变幅杆的等效电路
依据等效电路法理论,分别得出复合变幅杆左边指数杆和右边悬链线杆的等效四端网络电路并连接在一起,可以得到复合变幅杆的等效电路如图3所示。由于变幅杆振动速度连续,所以有v12=v21。
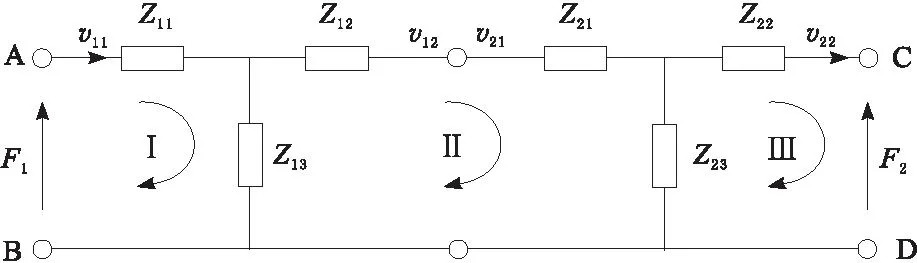
图3 复合变幅杆等效电路模型
左边指数杆等效电路参数为:
(1)
(2)
(3)
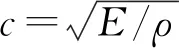
右边悬链线杆等效电路参数为:
(4)
(5)
(6)
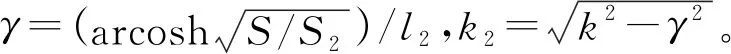
2.3 复合变幅杆的参数求解
当变幅杆两端自由时,复合变幅杆等效电路图3中F1=F2=0,输入端AB和输出端CD可视为短路,依据基尔霍夫回路电压定律(KVL)可得以下表达式。
回路Ⅰ:
v11(Z11+Z13)-v12Z13=0
(7)
回路Ⅱ:
-v11Z13+v12(Z13+Z12+Z21+Z23)-
v22Z23=0
(8)
回路Ⅲ:
-v12Z23+v22(Z23+Z22)=0
(9)
将式(7)的v11和式(9)的v22代入式(8)可得到复合变幅杆的频率方程为
(10)
由式(7)和式(9)消去v12,并代入相应的力阻抗可以得出复合变幅杆的放大系数为
(11)
3 复合变幅杆的优化设计
3.1 设计实例
该复合形变幅杆选用45号钢,材料密度ρ=7.81×103kg/m3,杨氏模量E=20.92×1010N/m2,泊松比μ=0.28,声速c=5 169 m/s,设计频率f=20 kHz,指数杆Ⅰ左侧端面的半径R1=26 mm,指数杆Ⅰ和悬链线杆Ⅱ交界面的半径R=16 mm,悬链线杆Ⅱ右侧端面的半径R2=8 mm,假设指数杆Ⅰ的长度为l1=78 mm,则可以利用MATLAB对频率方程(10)求数值解,算出悬链线杆Ⅱ的长度l2=71 mm,再由式(11)求出复合形变幅杆的放大系数MP=3.7。
3.2 优化分析
为了寻找放大系数更大的变幅杆,将对变幅杆进行优化设计,优化的思路是通过改变指数杆的长度l1和交界面的半径R,从而改变悬链线杆和复合变幅杆的谐振长度以及放大系数。
在保持指数杆Ⅰ左侧端面半径R1和悬链线杆Ⅱ右侧端面半径R2不变的情况下,复合变幅杆的谐振长度l1+l2和放大系数MP随交界面的半径R和指数杆的长度l1的变化关系分别如图4和图5所示。
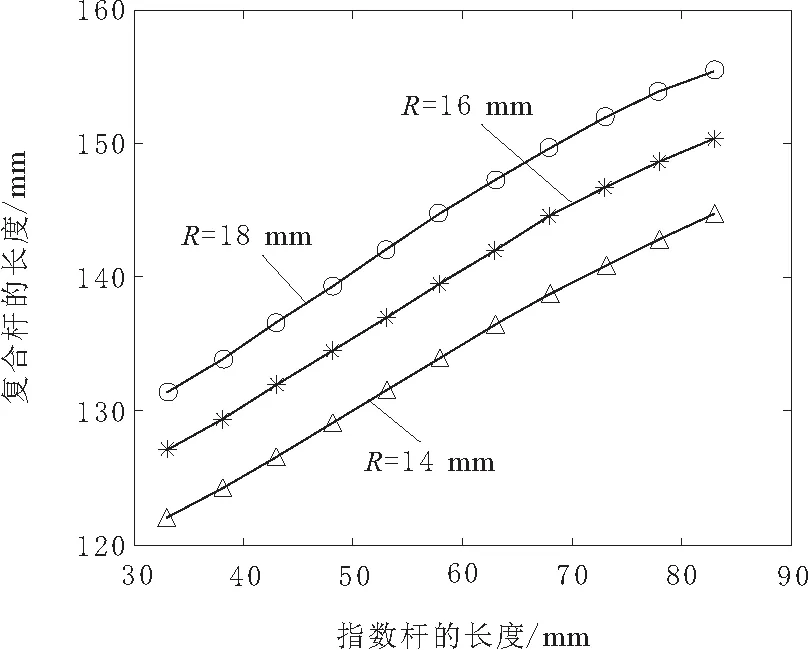
图4 复合变幅杆的长度变化规律
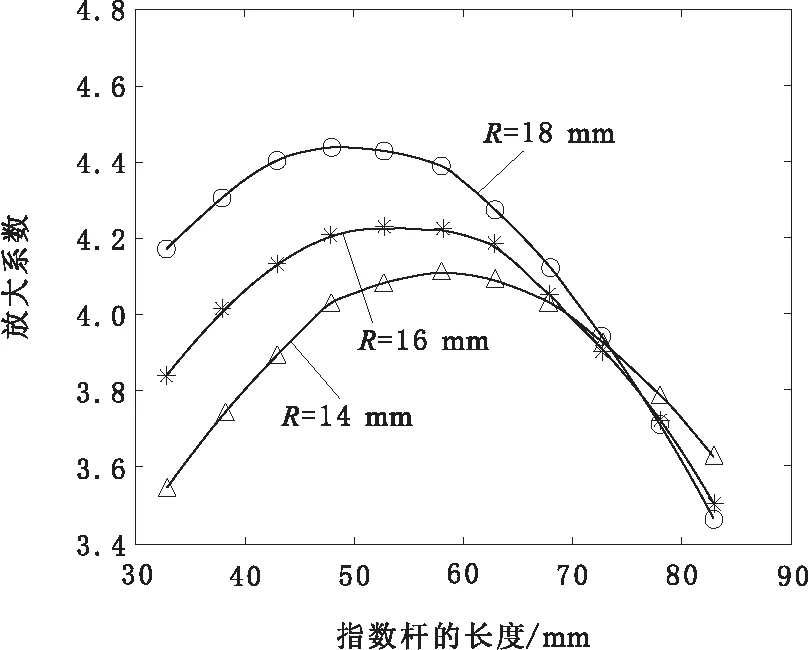
图5 复合变幅杆的放大系数变化规律
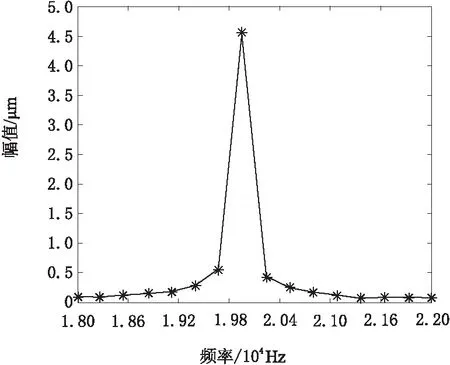
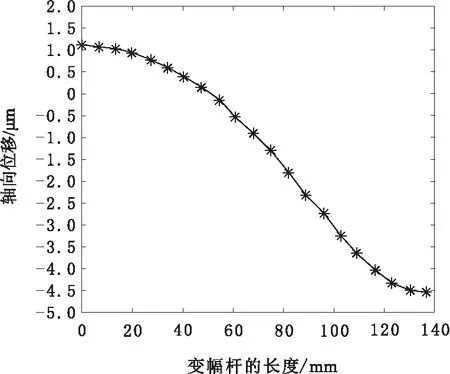
从图4可知,复合变幅杆的谐振长度l1+l2随着指数杆的长度l1的增大而增大,悬链线杆的长度l2随着指数杆的长度l1的增大而减小,在45 mm 从图5可知,复合变幅杆的放大系数MP随着指数杆长度l1的增大先增大后减小,在l1<68 mm的区域放大系数MP随着交界面的半径R的增大而增大,在放大系数MP达到最大值后对应的指数杆长度随交界面的半径R的增大而减小。当R=16 mm时放大系数MP达到最大值对应的指数杆长度为l1=53 mm,悬链线杆的长度为l2=84 mm,将参数代入式(11)可以求出优化后变幅杆的放大系数为4.2,比优化前提高了13.5%。 为了检验理论设计和优化分析的正确性,利用ANSYS软件对复合形变幅杆进行有限元分析。除指数杆Ⅰ长度取l1=53 mm和悬链线杆Ⅱ的长度l2=84 mm外,复合形变幅杆的材料参数、几何尺寸和谐振频率均和3.1节设计实例相同。 首先建立复合变幅杆的几何模型,依据设计尺寸计算出关键点的坐标并生成关键点,将关键点依次连接成线再生成面,以复合变幅杆中心线为轴旋转360°成体,选用SOLID95实体单元,采用扫掠网格划分,共得到7 861个节点和1 584个单元。运用分块兰索法(block Lanczos)分析,模态提取频率范围为18~22 kHz,使用Solve求解并提取与设计频率最接近的谐振模态如图6所示。由图6可以看出当谐振频率f′=19 839 Hz时,变幅杆做纵向振动状态良好,与理论设计基本吻合。 图6 复合变幅杆的位移云图 在模态分析的基础上,采用完全法(full)进行谐响应分析,这种方法是运用完整的系统矩阵来计算响应的。在圆柱杆的左端面加载幅值为1.1 μm的正弦变化的周期位移载荷,在变幅杆的输出端即悬链线杆的小端面输出的谐响应曲线如图7所示,从响应曲线可以看出,在谐振频率为19 839 Hz附近出现了振幅最大值。变幅杆的轴向位移曲线如图8所示,从图8可以看出变幅杆大小端面位移分别为1.1 μm和4.6 μm,可得到放大倍数约为4.1,将有限元分析结果与理论计算值进行比较,谐振频率相差0.8 %,放大倍数相差2.3 %,有限元分析结果与理论设计基本一致,符合变幅杆设计要求。 图7 谐响应曲线 图8 变幅杆的轴向位移曲线 利用等效电路法设计了一种新型的指数悬链线形复合变幅杆,并对变幅杆的设计进行优化和有限元分析。结果表明: a.复合变幅杆的谐振长度随着指数杆长度l1的增大而增大,但悬链线杆的长度l2随着指数杆长度的增大而减小;复合变幅杆的放大系数MP随着指数杆长度l1的增大先增大后减小,在l1<68 mm的区域放大系数MP随着交界面的半径R的增大而增大,在放大系数MP达到最大值后对应的指数杆长度随交界面的半径R的增大而减小;通过优化设计使复合变幅杆的放大系数从3.7增加到4.2,提高了13.5 %,为找到性能更优的变幅杆提供了思路。 b.利用等效电路法设计复合形变幅杆思路清晰,物理意义明确,设计精度符合要求,采用该方法可以将其他任意形状的变幅杆进行组合得出新型变幅杆,为变幅杆的优化设计提供了参考,有一定的实用价值。 c.有限元分析结果与理论设计基本一致,进一步证明了复合形变幅杆设计及优化的可靠性。4 有限元分析
4.1 模态分析
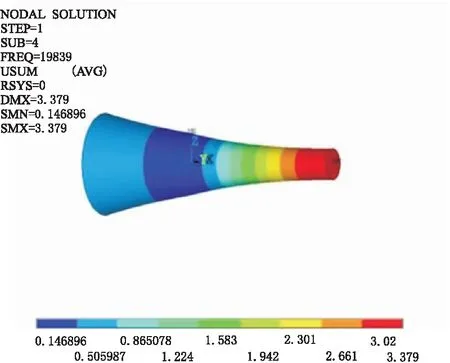
4.2 谐响应分析
5 结束语
